聚脲- 编织玻璃纤维网格布复合材料加固钢板抗冲击力学性能研究

廖瑜， 石少卿， 梁朝科， 王文康

(1.陆军勤务学院 土木工程系， 重庆 401331； 2.中国兵器装备集团有限公司 重庆红宇精密工业有限责任公司， 重庆 402760)

0 引言

简易爆炸装置(IED)俗称“路边炸弹”，是一种取材广泛、制作简便且爆炸威力巨大的一种爆炸装置。自阿富汗战争以来，恐怖分子常采用IED进行不对称战争反击，造成大量装甲车辆、防护结构和民用基础设施破坏。因此，提升现有结构在IED产生的爆炸和冲击波载荷下的生存能力一直是防护研究的热点问题。为此学者们提出了各种提升现有结构抗冲击力学性能方案，其中有研究表明高聚物弹性体具有较好的抗冲击防护效果。聚脲(PU)作为典型的高聚物弹性材料，与其他高聚物弹性材料相比，具有弹性模量高、抗拉强度大(12～45 MPa)、延展性高、抗冲击性能好的特点[1-2]。研究发现，钢板背面涂覆一定厚度的PU涂层能减小钢板整体变形[3-5],衰减钢板峰值速度[6]，增加冲击能耗[7]，阻止钢板背面层裂碎片飞散[8]。将PU涂覆于钢板的迎爆面时，PU在高温爆轰产物作用下发生熔化[9]，而无法发挥PU力学性能。此外，由于PU的波阻抗小于被加固结构，涂覆于结构表面的PU对入射冲击波荷载具有放大作用[10]。因此，PU常作为保护涂层涂覆于结构背面。

一般来说，PU涂层厚度越大，越有利于提升结构的抗冲击力学性能[11-12]，但单纯通过增加PU涂层厚度的方法来提升结构的抗冲击力学性能因价格原因不实际。鉴于PU的延展性较高而弹性模量较低的力学特点，学者们考虑将具有高弹性模量和高强度的纤维材料与其组成复合材料。Greene等[13]和Carey等[14]发现，在PU基体中添加一定体积分数的短切玻璃纤维不仅能减轻爆炸碎片的飞散，还能提升结构的抗剪力学性能。Nantasetphong等[15-16]在PU基体中添加碾磨玻璃纤维粉(MG)合成PU-MG复合材料，通过动态力学分析测试表明MG可提升复合材料的弹性模量。Ha等[17]在碳纤维布(CFRP)的背面喷涂一层PU涂层，组成PU-CFRP复合结构。研究表明，在质量为15.88 kg、爆距为1.5 m的铵油炸药作用下，采用PU-CFRP复合结构加固钢筋混凝土板的损伤范围最小。

目前，常用的纤维主要有碳纤维、玻璃纤维和芳纶纤维。由于玻璃纤维的延展性介于碳纤维和芳纶纤维之间，且价格远低于碳纤维和芳纶纤维，本文选用玻璃纤维作为复合材料的增强体。此外，由于与编织玻璃纤维布相比，编织玻璃纤维网格布(WFM)轻质、价格便宜[18]，本文选用WFM作为复合材料的增强体，与PU基体组成PU-WFM复合材料。在PU-WFM复合材料中，WFM对PU基体的增强作用与钢筋混凝土中的钢筋相似，即发挥“软钢筋”的作用。

本文采用有限元仿真模拟软件ANSYS/ LS-DYNA对比研究了峰值压力为0.47 MPa的平面冲击波荷载作用下，PU加固层和包含不同层数WFM的PU-WFM复合材料加固层加固钢板的抗冲击力学性能，并通过大型激波管试验结果验证了数值计算结果的可靠性。

1 数值计算模型

1.1 材料模型及参数

1.1.1 PU模型及参数

PU是异氰酸酯(A组分)和树脂(B组分)反应生成的一种弹性体物质。根据PU的力学性能，所选材料模型应包含弹性段和塑性段，用以描述PU的变形，同时可描述PU的应变率相关性[3,19]。因此，本文采用MAT_PIECEWISE_LINEAR_PLASTICITY弹塑性材料模型来描述PU的力学性能。该材料模型需要输入物理力学性能参数、真应力- 有效应变曲线和应变率- 屈服强度曲线完成定义。

为获得PU物理力学性能参数和真应力- 有效应变曲线，根据国家标准GB/T528—2009 硫化橡胶或热塑性橡胶拉伸应力应变性能的测定[20]，在美国ITW集团公司生产的Instron-3365万能试验机上进行了PU准静态拉伸力学性能试验。其中，试件采用Ⅰ型哑铃型件，试样的加载应变速率设定为 0.25 s-1. 经过数据处理，得到PU的工程应力- 工程应变和真应力- 真应变曲线如图1所示。有效应变εe计算公式为

(1)

式中：εT为真应变；E为弹性模量；σ0为准静态条件下PU的屈服强度。材料模型各参数值为：密度ρ=1.12 g/cm3，泊松比ν=0.4，剪切模量Et=5.6 MPa，E=171 MPa，屈服应力σy=6.0 MPa.

PU的应变率效应可通过基于Cowper-Symbols模型和拟合实测数据建立应变率与屈服应力σy、动态增强因子DIF的关系。然而，Raman等[21]发现采用(2)式和(3)式可更好地描述PU应变率与屈服应力σy、动态增强因子DIF间的关系：

(2)

σy=σ0DIF,

(3)

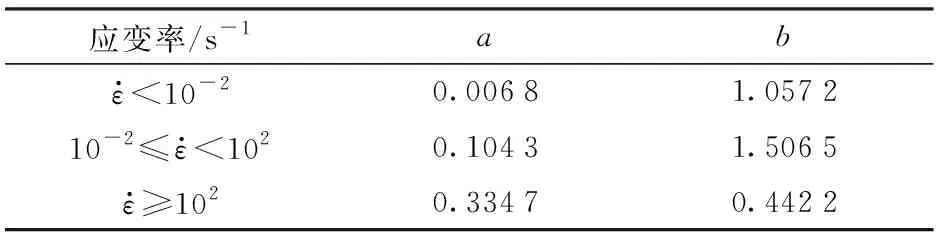
表1 不同应变率下屈服应力增强因子的拟合系数

1.1.2 WFM模型及参数

WFM是由经向和纬向玻璃纤维纱绞织组成的一种理想弹性材料。由于WFM的经向和纬向玻璃纤维纱长度方向尺寸远大于其厚度和宽度，本文借鉴文献[18]对编织玄武岩纤维网格布的处理方法，忽略经向纤维和纬向纤维厚度方向和宽度方向的材料力学性能。将WFM简化为由均质化经向和纬向纤维组成的网格布。因此，可利用经向与纬向纤维的几何尺寸差异来描述网格布0°与90°方向的力学性能差异，如图2所示。

本文采用MAT_ELASTIC理想线弹性模型来模拟WFM的力学性能。其中WFM的规格为120 g/cm2，经向纤维宽度为1.80 mm，厚度为0.10 mm，而纬向纤维宽度为0.40 mm，厚度为0.40 mm，网孔尺寸为5 mm×5 mm. 材料模型各参数取值[22]为ρ=2.49 g/cm3，ν=0.22，E=100.7 GPa.

1.1.3 钢板模型及参数

冲击波作用下，钢板将处于高压和高应变率状态。因而本文选用基于金属材料发生大变形、高应变率和不同温度条件的Johnson-Cook材料模型。Johnson-Cook材料模型是基于von Mises屈服应力的模型，其表达式为

(4)

材料断裂应变表达式为

(5)

式中：σ*=p/σe，p为压力，σe为von Mises等效应力；D1～D5为材料参数。当损伤参数D=∑Δε/εf=1.0时发生断裂，其中Δε为积分循环塑性应变增量。试验用Q235钢的Johnson-Cook材料模型参数[23]为ρ=7.80 g/cm3，A=229 MPa，B=439.0 MPa，n=0.503，C=0.1，m=0.55，D1=0.3，D2=0.9，D3=-2.8，D4=0，D5=0.

1.2 荷载

激波管中传播的冲击波荷载具有强间断性，且其波形具有爆炸冲击波波形的一般特征[24]。为防止锯齿状压力时程曲线对数值计算过程造成非线性扰动，模型施加冲击波压力荷载时需要对实测压力时程曲线(见图3)进行光滑处理。

本文采用数据拟合方法对原始压力时程曲线进行光滑处理，得

(6)

1.3 有限元建模

利用ANSYS前处理软件对PU-WFM复合材料加固钢板进行三维实体建模，数值模拟所选取的计算模型与实体一致。在数值模拟中，利用问题的对称性，采用1/4模型，并在对称面上施加对称约束。模型由4部分组成，即钢板、PU基体、经向玻璃纤维和纬向玻璃纤维，1/4计算模型和加固层局部放大图如图4所示。

除WFM采用线性3节点Belytsckcho-Schwer梁单元，其余部分均采用8节点六面体实体单元Solid164. 钢板和加固层的网格最小尺寸为1 mm，经向玻璃纤维和纬向玻璃纤维的网格最小尺寸为2.5 mm，模型的单元总数为201 100.

PU-WFM复合材料模型建立时，首先确立WFM在PU基体中的位置，然后将WFM单元插入PU单元空间，利用关键字*CONSTRAINED_LAGRANG_IN_SOLID实现PU和纤维节点间的耦合。加固层与钢板间采用固连接触算法*CONTACT_TIEDBREAK_SURFACE_TO_ SURFACE_OFFSET来描述。该关键字的界面失效定义为

(7)

式中：σn和σs分别为界面处的拉应力和剪应力；NFLS和SFLS分别为极限拉应力和极限剪应力，其中NFLS=64 MPa，SFLS=100 MPa[25].

为模拟冲击波荷载作用下，无限大钢板的局域化损伤问题，PU-WFM复合材料加固钢板模型的边界设置为位移全约束。模型冲击波荷载的施加通过关键字*SET_SEGMENT和*LOAD_SEGMENT_SET实现。

1.4 数值计算方案

针对未加固钢板(K-1)、PU加固钢板(P-1)、包含1层WFM的PU-WFM复合材料加固钢板(C-1)、包含2层WFM的PU-WFM复合材料加固钢板(C-2)和包含3层WFM的PU-WFM复合材料加固钢板(C-3)进行仿真模拟计算。所有计算模型中，被加固钢板尺寸和加固层厚度相同，其中钢板尺寸为600 mm×400 mm×3 mm，加固层厚度为3.5 mm. C-1试件、C-2试件和C-3试件中WFM在PU基体内的位置分别如图5(a)、图5(b)和图5(c)所示。值得注意的是，WFM在加固层中可达到的最小间距为0.9 mm，即3层WFM是3.5 mm厚加固层所容许的最大添加层数。平面冲击波荷载的峰值压力为0.47 MPa.

2 数值模拟结果分析

2.1 试件变形分析

首先对比相同冲击波载荷下被加固钢板的变形情况，图6为被加固钢板变形最大时的z向位移云图。由图6可见，未加固钢板试件(K-1)的整体变形最大，PU加固钢板试件(P-1)次之，PU-WFM复合材料加固钢板试件最小。在PU-WFM复合材料加固试件中，C-3试件的整体变形最小，C-1～C-3试件的变形情况如图6(c)、图6(d)和图6(e)所示，说明PU基体中所添加WFM层数越多，越有利于减小钢板整体变形。

图7为被加固钢板的板中心位移时程曲线图。从图7可知，与K-1试件相比，其余试件到达峰值位移的时间延后，说明加固层可以减小钢板的变形速率。对比试件z向峰值位移可知，K-1试件的峰值位移为14.47 mm，P-1试件的峰值位移为14.44 mm，说明传统纯PU加固层减小钢板峰值位移的作用有限。而当钢板采用PU-WFM复合材料加固时，C-1试件的峰值位移为13.67 mm，C-2试件的峰值位移为13.10 mm，C-3试件的峰值位移为12.68 mm. 与K-1试件相比，C-1～C-3试件的峰值位移分别减小5.53%、9.47%和12.37%. 由此可见，与传统PU加固层相比，PU-WFM复合材料可减小钢板的峰值位移，且纤维增强体的层数越多，被加固钢板峰值位移越小，加固层的加固性能越好。

图8为钢板变形最大时加固层的应力分布情况，其中加固层的应力分布用数值模拟von Mises应力云图来描述。从图8可知，Von Mises应力大小按照P-1试件、C-1试件、C-2试件和C-3试件的顺序依次递减，分别如图8(a)、图8(b)、图8(c)和图8(d)所示。因此，WFM可减小加固层中心区域的应力集中效应，降低PU加固层发生破坏的风险，且随着WFM层数的增加，试件中心区域的应力相应减小。

2.2 钢板动能及加固层内能分析

冲击波荷载作用下，被加固钢板的动能和加固层的内能是衡量加固层加固性能的重要指标。图9 为钢板涂覆不同加固层时的动能时程曲线。由图9可知， P-1试件的峰值动能小于K-1试件，二者峰值动能分别为2.43 kJ和2.75 kJ. 随着PU基体中添加的WFM层数的增加，被加固钢板的峰值动能进一步降低，其中C-1试件的峰值动能为2.24 kJ，C-2试件的峰值动能为2.12 kJ，C-3试件的峰值动能为1.98 kJ. 与K-1试件相比，P-1试件、C-1试件、C-2试件和C-3试件的峰值动能分别减小11.63%、12.00%、22.90%和28.00%.

图10为不同加固层的内能对比图。由图10可知，P-1试件加固层的内能为0.12 kJ，C-1试件加固层内能为0.16 kJ，C-2试件加固层内能为0.23 kJ，C-3试件加固层内能为0.43 kJ. 与纯PU加固层相比，C-1试件加固层、C-2试件加固层和C-3试件加固层的内能分别增加33.33%、91.67%和175%. 显然，加固层的内能随WFM层数的增加呈现指数递增变化。因此，PU基体中WFM层数越多，加固层内能越大，吸收冲击波荷载能量相应增加。

3 试验验证

为验证数值计算结论的正确性和可靠性，采用大型激波管试验设备，对P-1试件和C-3试件进行了试验研究。试件抗冲击试验在陆军医科大学激波管实验室进行，激波管总长为39 m，试验段内径为1 m，分为高压段、夹膜段(两个膜片)、扩散段、试验段和消波段，如图11所示。

被加固钢板的尺寸与前文一致，均为600 mm×400 mm×3 mm. P-1试件加固层的平均厚度约为3.2 mm，C-3试件加固层的平均厚度约为3.5 mm，且WFM在PU基体中的位置与数值模拟一致。

为防止冲击波绕流对测试结果造成影响，试件安放于密闭的钢箱上。同时为模拟无限大板的局部损伤问题，设计了由槽钢、钢框架、钢块和螺栓组成的夹持系统对试件进行固定和约束，如图12(a)所示。同时被加固钢板表面涂抹松香以增大夹持系统对试件的约束力，试件装配效果如图12(b)所示。

为获得能用于验证数值计算模型正确性的有效试验测试数据，在加固层背面对角线上的中点和对角线1/4处分别粘贴1组呈0°与90°布置的应变片。应变数据的采集采用江苏泰斯特电子设备制造有限公司生产的TST5912动态数据采集系统。

压力数据的采集使用美国IOTECH公司生产的WAVEBOOK/512数据采集系统，压力传感器采用美国PCB公司生产的M102A02压电式压力传感器，精度为±0.025%FS，采样频率为1 MHz. 其中压力传感器安装于管壁上，与被测试件表面等高。

经测量，作用于P-1试件和C-3试件的冲击波峰值超压值相近，分别为464 kPa和467 kPa. 由于PU加固层与PU-WFM加固层厚度几乎相同，二者间可进行定量分析。

图13为冲击试验后试件变形的试验与数值模拟结果对比，其中数值模拟结果采用von Mises应变云图来描述。从图13可知，试验和数值模拟均显示P-1试件板中心的变形和对称线弯曲程度都大于C-3试件。经测量：P-1试件中心处残余位移的试验与数值模拟结果分别为11.05 mm和12.02 mm，相对误差为8.78%；C-3试件中心处残余位移的试验与数值模拟结果分别为9.83 mm和10.32 mm，相对误差仅为4.98%.

图14为激波管冲击试验后，PU加固层与PU-WFM加固层的变形对比，其中数值模拟结果采用von Mises应变云图来描述。从图14可知，数值模拟结果和试验结果均显示PU加固层的变形大于PU-WFM加固层变形，说明本文所建立的有限元计算模型能很好地模拟冲击波荷载作用后试件的变形特征。

为进一步校核本文有限元计算模型描述试件动态力学性能的可靠性，采用PU加固层和PU-WFM加固层对角线1/4处的0°方向应变时程曲线作为研究对象。

图15为试验与数值模拟的应变时程曲线结果对比。由图15可知，受冲击波荷载作用，测点处应变突跃升高，随后呈指数衰减，数值模拟很好地捕捉到了测点处应变的变化规律。其中P-1试件的峰值应变试验与数值模拟结果分别为3 331.20×10-6和3 599.23×10-6，相对误差为8.05%；而C-3试件的峰值应变试验与数值模拟结果分别为2 625.53×10-6和3 000.68×10-6，相对误差为14.28%. 鉴于激波管冲击试验数值模拟的复杂性，说明本文所建立的有限元计算模型能准确预测PU-WFM复合材料加固钢板的动态力学性能。

4 结论

本文采用有限元数值模拟方法对PU加固层和包含不同层数WFM的PU-WFM复合材料加固层加固钢板的抗冲击力学性能进行研究，并采用激波管现场冲击试验验证了数值计算模型的正确性，得出如下结论：

1)WFM可提升PU加固层的加固性能，且WFM层数越多，对PU加固层的加固性能提升越大。

2)加固层厚度相同条件下，PU-WFM复合材料加固层可减小被加固钢板整体变形和钢板中心峰值位移，而传统PU加固层在减小被加固钢板变形方面的作用有限。

3)在WFM层数容许添加范围内，尽管PU加固层和PU-WFM复合材料加固层均可减小被加固钢板动能，但与PU加固层相比，钢板采用PU-WFM复合材料加固层后动能最大可减小28%；此外，PU-WFM复合材料加固层的内能最大可达到相同厚度纯PU加固层的2.75倍。

4)数值模拟结果与现场激波管冲击试验结果基本一致，表明本文数值计算结果的可靠性，可以为采用WFM及类似小网孔材料作为增强体提升基体加固性能的工程实践提供参考。