锚板抗拔理论在地下储气洞室中的应用

匡根林， 许 萍

(1.湘潭市水利水电勘测设计院， 湖南 湘潭 411100； 2.西安理工大学 水利水电学院， 陕西 西安 710048)

随着社会经济和技术的迅速发展以及世界人口的增长，全球环境、能源等问题日益突出。可再生能源的开发利用已成为世界各国的共识[1]。可再生能源大规模发展往往需要储能技术的支撑，开发和利用地下空间储能是实现土地的多重利用，实现“资源节约型”城市的重要方面，更是可持续发展战略中的一项重大措施。压气储能(Compressed Air Energy Storage，简称CAES)是一种利用压缩空气作为介质来储存能量和发电的技术。该技术最早在1949年被Stal Laval提出以来，经过大量相关研究和技术论证，已经实现大规模商业化应用，例如位于德国托夫市(Huntorf)和美国阿拉巴马州迈金托夫市(Mcintosh)已有两座压气储能示范电站(CAES)投入运营，输出功率分别为290 MW、110 MW[2]。具体做法是在电网负荷低谷期将电能用于压缩空气，将空气高压密封在储气罐或山洞、报废矿井等地下洞室中，在电网负荷高峰期释放压缩空气推动汽轮机发电[3]。那么在此过程中如何利用岩体来抵抗地下储气洞室中的气体压力(存储压力可达10 MPa以上)，并且维持洞室围岩自身的稳定则是我们岩土工作者亟需解决的关键问题。

然而现今鲜有关于地下高压储气洞室的相关研究，这是由于现代压缩空气储存往往采用地面储气罐取代地下洞室，然而很明显如果存在合适的地下矿井或熔岩下的洞室中则是压缩空气储能的最环保最经济的方式。然而对于地下高压储气洞[4]，目前还没有统一的计算理论和规定，利用水工理论上抬准则[5]计算的需要岩石覆盖层厚度往往较大，不仅影响工程的经济性，而且给工程施工及运行管理也带来诸多不便。因此，寻求一种合理的地下高压储气洞室岩体覆盖厚度计算方法，对于地下高压储气库等类似工程的设计与建造至关重要。

通过研究比较，笔者发现实践中广泛应用的水平抗拔锚板的受力形式与地下高压储气室顶部围岩受力形式非常相似。诚然，若地下高压储气洞室埋置深度足够深，洞室顶部的岩石覆盖层足够厚，在高压下不会形成贯穿顶部的破裂面，洞室就能够安全运行，但是深埋深挖不仅带来建造施工及运行管理等方面的不利，更使得工程项目不经济，因此不考虑深埋型。本文拟运用浅埋型的锚板理论，尝试从水平抗拔锚板承载力研究理论出发，寻找一种计算地下高压储气室岩石覆盖厚度的新方法，以期为实际地下储气洞室工程建设提供指导。

1 水平锚板抗拔力

锚板主要作用是为结构提供抗拔承载力，抗拔锚板由于其方便、实用和经济等特点被广泛应用于高耸结构和其他承受上拔荷载作用的建筑结构中[6]。抗拔锚板承载力以及抗拔锚板破坏形式等研究一直是个重点，同时也积累了大量理论研究成果[7-12]。

1.1 锚板基础的破裂面形式

根据以往的研究可以归纳出四种主要的研究方法。(1) 根据原位试验和室内模型试验结果，通过数值拟合求得一系列经验公式；(2) 假设应力许可的位移场或机动许可的速度场，根据极限分析的上下限定理计算抗拔锚板的极限承载力；(3) 假设抗拔锚板的破裂面方程，根据极限平衡原理计算抗拔锚板的承载力；(4) 采用有限元、边界元等数值分析方法来计算抗拔基础的承载力。其中(1)和(3)这两种方法应用较多。利用极限平衡研究原理，根据上部岩土块体抵抗力考虑的因素不同，锚板分析方法又可以分为重力法、剪切模式计算法和被动土压力半经验法等。重力法应用较早，以Majer和Mors的理论为代表，1958年日本电工技术委员会(JEC)将其纳入规范中，该方法只考虑破坏面上部块体的重量，不考虑剪切作用，计算结果和实际差距很大。剪切模式计算法如果假定直面破坏形式(见图1)，那与实际差距也很大。Balla和Matsuo分别假定圆弧形式的破坏面和对数螺旋型破坏面，与实际更为接近，见图2～图3。

图1 直面破坏

图2 斜面破坏图

图3曲面破坏

通过现有研究结果表明，锚板的埋置深度和几何形状是影响锚板基础破坏形式的两个重要因素。为分析方便往往采用一个综合参数埋深率(H/D)来表示，其中H表示埋置深度，D表示锚板的长度。浅埋型锚板和深埋型锚板的临界埋深率(H/D)cr在4～6之间。对于浅埋型的锚板基础破坏面形式，主要可以归为三种：直面破坏形式、斜面破坏形式和曲面破坏形式，见图1～图3。而现有的锚板研究理论大多倾向于斜面破坏和曲面破坏形式。

Meyerhof 和Adams于1968年提出基于模型试验的半经验方法，根据在砂和粘土中的实验结果指出，对于小于临界埋深率的浅埋锚板基础，抗拔承载力随着埋深的增加而增加，在密实的砂中可以观察到明显的滑动破坏面，从基础边缘开始以一定的弧形向地表面延伸。而后，也有不少学者得出了相似的结论。当锚板上部基础在外部极限拉力的作用下，浅埋型(H/D<6)锚板基础的破坏面形式为一曲面，可近似为斜面来研究，并且该破坏面直线和铅直面的夹角(斜面破坏的θ角)为φ/2+2°，其中φ为内摩擦角；采用室内足尺寸模型试验对钙质砂中锚板的抗拔破坏面形式研究发现，浅埋型破坏面形式往往为贯穿至砂体表面的曲面。由此可知浅埋锚板的基础而言，斜面破坏和曲面破坏更接近实际，直面破坏更保守。

1.2 圆形锚板基础的破裂面参数方程

根据曲面破坏形式，何思明[13]给出了圆形锚板基础的破裂面方程：

(1)

式中：r为圆形锚板基础的半径；H为锚板的埋深；φ为土的内摩擦角；n为待定系数；z为锚板的几何长度。一般的，锚板埋深H均大于锚板长度z。

该破裂面在空间上为回转面，见图4。对该种曲面破裂面形式做以下两种特例进行分析讨论。

图4圆形锚板破裂面形式

当参数n趋于无穷大时，对式(1)两边取极限，由于H大于z，可得

x=r

(2)

破裂面为半径为r的圆柱面，和Majer的理论相似。

当参数n趋于零时，对式(1)两边取极限，可得

x=r+z/tan(45°-φ/2)

(3)

破裂面为圆锥面，即为上文所述的斜面破坏形式，斜面倾角为45°-φ/2。

上面两种特例对应的锚板基础破裂面就是目前计算抗拔锚板基础承载力时通常采用的基本假定。

2 地下高压储气室

作为压气储能电站主要组成部分的地下高压储气室是保障压气储能电站运行性能和可靠性的关键技术。美国于1981年启动的Soyland压气储能项目，利用硬岩洞室作为高压储气室，最终以失败告终[14]。地下储气洞室受力复杂，仅对于洞室方案选型来说，仅单纯考虑洞室稳定性而不兼顾洞室密封性能以及密封材料受温度影响耐久性等是远远不够的[15-16]。

2.1 受力简化

在内部高压气体的挤压下，地下高压储气室内壁受力见示意图5。此时，地下有压洞室顶部承受内部压力，可近似看成一个集中力P作用在顶部中心位置，把储气洞室顶部假想成一个和该洞室水平投影面大小相同的锚板，这个集中力作用在锚板中心(见图6)。由于顶部为圆形地下高压储气洞室受力条件较好，且应用广泛，因此本文仅从地下立式储气洞出发，假定洞室围岩均一，不考虑围岩地质差别，利用圆形锚板理论来研究有压洞室顶部的合理的围岩厚度计算。

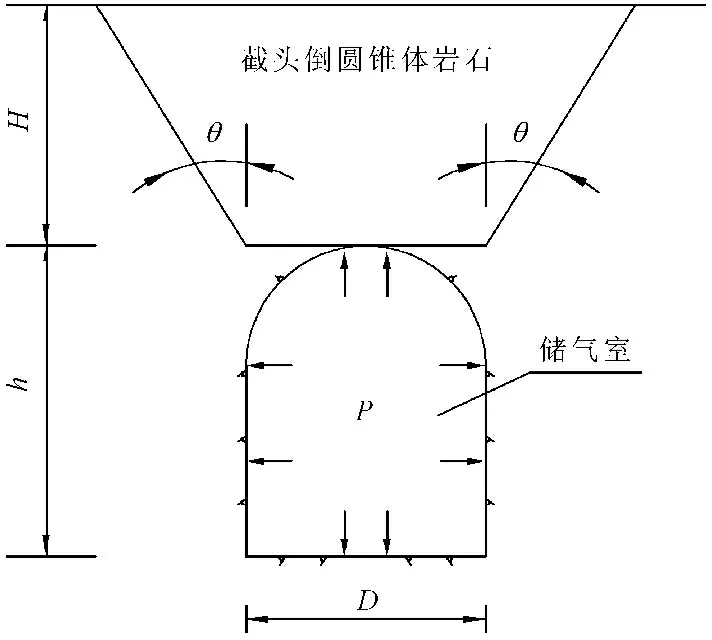
图5地下高压储气洞受力示意

2.2 地下高压储气室破坏形式

基于上述对抗拔锚板破坏形式的分析研究，圆形锚板基础的破裂面形式以斜面破坏和曲面破坏更接近实际。故本文主要针对斜面破坏和曲面两种锚板破坏形式，同时采用重力法和剪切法分别确定其承载力计算确定高压储气室顶部的最小围岩厚度。

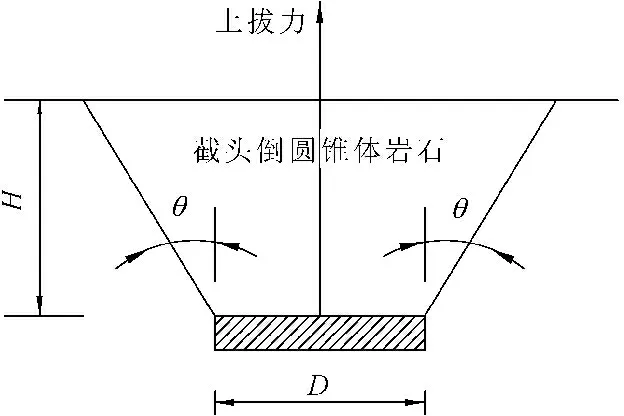
图6地下高压储气洞受力简图

2.2.1 重力法确定承载力计算

采用重力法确定承载力，应用斜面破坏模式(参见图7)，不考虑破裂面上剪切阻力，仅考虑这个截头倒圆锥的重量W，该值唯一抵抗地下储气室顶部所受的垂向内部压力P，根据垂向的受力可以计算稳定安全系数Fs，可分别以下计算公式获得：

(4)

P=πr2p

(5)

Fs=W/P

(6)

式(4)～式(6)中，ρ为土的密度；g为重力加速度；r为储气洞室的半径；d为储气室埋深；α为锥角，根据文献[4]，α=30°～45°，也可以按上文的提到的φ/2+2°和45°-φ/2所确定。

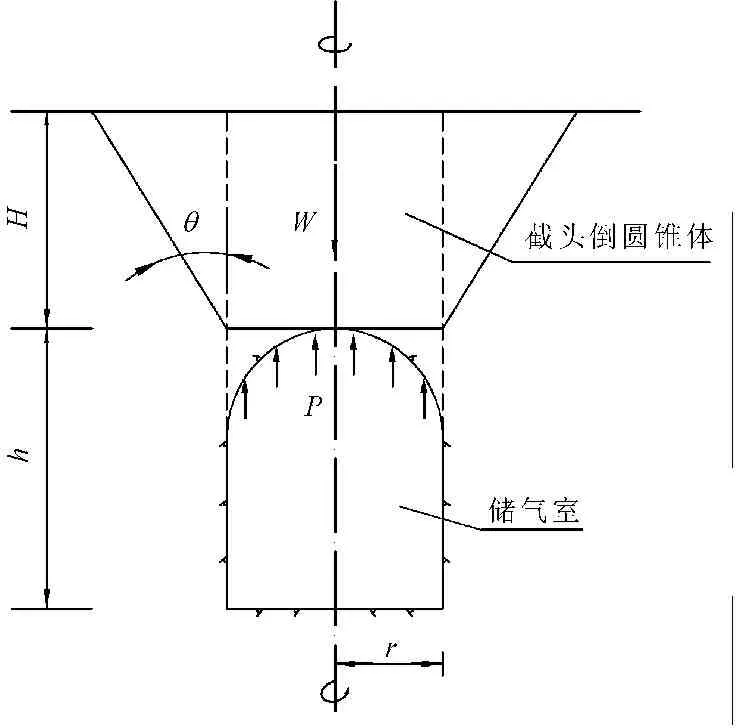
图7斜面破坏模式

该方法比较保守，但是概念清晰，计算参数简单。若给定储气室几何参数和锥角α，亦可根据内部压力P以及设计要求的安全系数Fs来确定最小的岩石覆盖厚度d。

2.2.2 剪切法确定承载力计算

采用剪切法确定承载力，应用曲面破坏模式(螺旋面)(见图8)，考虑曲面上部的块体重量W和曲面上的剪切阻力f，根据垂向受力分析可以计算稳定安全系数Fs。

对数螺旋破坏面方程：

rw=r0ewtanφ

(7)

Fs=W/P

(8)

式(7)中，rw角度为w时的螺旋线半径；r0为0角度时螺旋线的半径；w为旋转角；φ为锚板基础的摩擦角。

图8曲面破坏模式

3 算 例

为了便于验证，设某一高压储气洞室设计参数为：有压储气洞半径r=20 m，内部压力p=10 MPa，上覆岩石厚度为H=150 m，岩石密度取为ρ=2 400 kg/m3，圆锥角α=30°。

首先假定储气洞室上部围岩破坏形式为斜面破坏，且不考虑破裂面上的滑动摩擦阻力作用，由于直径为D=40 m，埋深为H=150 m，有H/D=3.75，根据锚板埋深率来划分，该储气室属浅埋型。按公式(4)计算出破裂面上部岩体重量为W=5.137×1010kN，按公式(5)计算出内部压力为P=1.257×107kN，按公式(6)计算所得安全系数为Fs=4.088。可见，在这种理论下，该储气室的上部岩石的覆盖厚度有很大的安全系数。由于曲面破坏的对数螺旋破坏面不易确定，这里暂不按这种方法计算。利用有限元软件FLAC对该工程进行数值模拟，结果表明，斜面破坏和对数螺旋曲线破坏面的假定偏于保守。

若采用水工领域常用的上抬准则[4]计算上述工程埋深，则需至少需要400 m的岩石覆盖厚度，并且安全系数只有1.000。若安全系数要到达同等安全系数4.088，则至少需要埋深1 600 m。

由此可见，对于同样的工程，比较利用锚板理论计算结果和上抬准则计算结果，很明显，利用上抬准则计算出的埋深，属于深埋型，对工程施工及以后的运行管理极为不便，严重影响工程经济性。而利用锚板理论计算的结果更为合理。

上述水平锚板理论仅考虑顶部岩石的重量是唯一抵抗地下压力洞室内部高压的作用力，没有考虑岩石沿着破裂面摩擦阻力，计算结果偏于安全。

4 结 论

从可持续发展的观点来看，地下储气洞室具有广阔的应用前景，完善地下高压储气洞室的设计理论和施工技术具有显著的经济和社会效益。本文在现有抗拔锚板理论研究的基础上，指出水平抗拔锚板的受力机理与地下高压储气洞室顶部受力基本类似，因此借鉴现有抗拔锚板成熟的研究成果应用于地下高压储气洞室，提出了重力法和剪切法确定上部围岩承载力计算公式，最终确定经济合理的岩层覆盖厚度。通过与确定水工隧洞最小覆盖层厚度的上抬准则计算结果进行对比，可以发现，本文采用的水平锚板理论设计高压储气洞室岩石覆盖层厚度比较适用。可以说从水平锚板抗拔力角度出发，对地下高压储气洞室岩石覆盖厚度计算作了一次有益的尝试，对类似工程设计具有一定的指导意义。