军民水库溢洪道堰面水动力特性试验研究

简鸿福，吕 辉，唐波华，罗 优

(1.江西省水利科学研究院， 江西 南昌 330029； 2.鄱阳县军民水库管理局， 江西 鄱阳 333100； 3.扬州大学 水利与能源动力工程学院, 江苏 扬州 225127)

溢洪道是水库洪水下泄的主要建筑物，其流量系数和泄流能力是水库调洪计算的重要参数[1-3]。溢洪道控制堰的堰型主要有实用堰、宽顶堰、驼峰堰等型式，其中，驼峰堰与宽顶堰相比，具有流量系数大、泄流及过砂能力强、整体稳定性较好、堰体外观漂亮等优点。目前驼峰堰一般修建在矩形明渠中，通过分别位于堰上、下游的两个扭曲渐变段与梯形断面的上游引渠和下游泄槽相连接[4-6]，这种布置形式与军民水库溢洪道现状为梯形明渠不一致，需要增加大量的石方爆破和混凝土浇筑，导致工程量的增加和施工难度的增大，堰上水流流态也变得复杂。

针对军民水库溢洪道现状为梯形明渠的问题，本文开展模型试验，提出将堰体直接修建在现有明渠中，省去了扭面渐变段的实施，减少了工程量和施工难度，改善了泄流条件，增加了泄流能力，并提出了符合工程实际的泄流能力计算方法，对同类工程具有参考意义。

1 工程概况

军民水库位于鄱阳县境内潼津河北支流上，坝址以上控制流域面积133 km2。正常蓄水位82.15 m，设计洪水位85.22 m，校核洪水位86.49 m，总库容1.894亿m3，主要建筑物包括：大坝、溢洪道、灌溉发电隧洞、灌溉兼放空底涵[7-8]。

溢洪道位于大坝右岸的山体垭口处，控制段为开敞式无闸控制驼峰堰，总长775.0 m，由进口引渠段、控制段、泄槽段、消能段、出水渠段、泄洪渠段组成。

控制段长16.4 m，渠底高程80.15 m，驼峰堰顶高程82.15 m，顶宽30.0 m，过流断面为梯形，两岸边坡为1∶1.0，由混凝土衬护。堰体采用C15埋石混凝土外包C20混凝土面板结构，面板最小厚度0.5 m。堰面曲线由三段弧组成，堰顶曲线半径5.0 m，上下游反弧曲线半径12.0 m。下反弧段与一级泄槽段直接相连，泄槽坡度为1/35。溢洪道进口及控制段布置图见图1～图3。

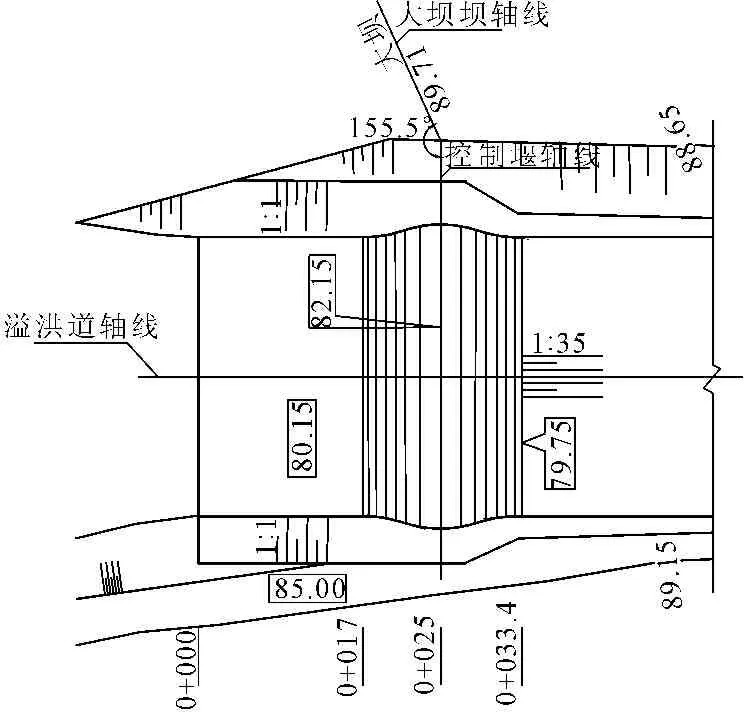
图1 溢洪道控制段平面布置图(单位：m)

图2溢洪道控制段纵剖面图

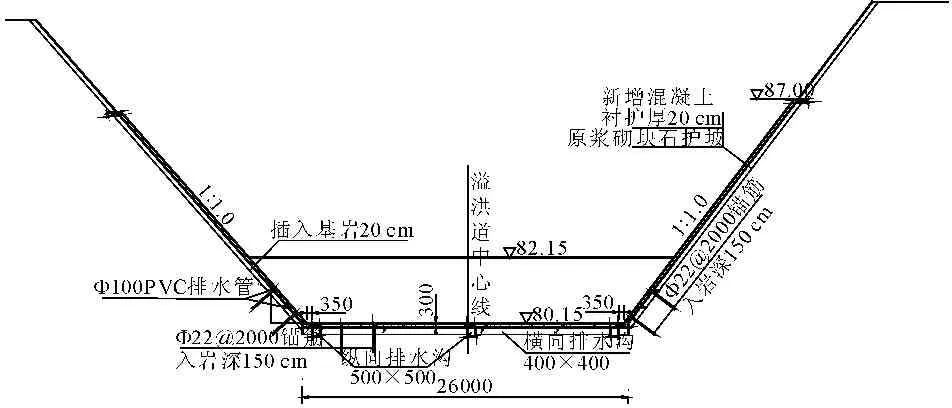
图3溢洪道控制段横剖面图

2 试验模型及参数

2.1 模型比尺

军民水库溢洪道模型按重力相似性准则设计，模型比尺(几何比尺Lr)的选取除满足重力相似要求外，还需满足阻力相似的要求[9-12]，即模型的糙率系数nm与原体的糙率系数np之间满足以下关系：

(1)

根据相关资料，原体中溢洪道表面为混凝土，np=0.014，模型中溢洪道的制模材料为有机玻璃，nm=0.0085，由此得到几何比尺Lr=19.96。综合考虑实验室条件及相关设备因素，确定模型比尺Lr=20，按重力相似准则得出相应的流速比尺Vr=200.5、流量比尺Qr=202.5、时间比尺Tr=200.5。

2.2 模型制作和安装

整个模型由进水系统、模型试验段、量水系统和回水系统等组成，为保证溢洪道进口水流条件相似，模型对溢洪道进水口前缘局部区域内的上游水库地形进行了模拟。模型进口引水渠、控制堰、泄槽及消力池均采用有机玻璃制作，上游水库地形用水泥砂浆抹制，交叉工程和泄水渠用灰塑料板制作。

2.3 试验测试方法和测试仪器

本次模型试验选择110.8 m3/s、175.9 m3/s、232.1 m3/s、309.7 m3/s、383.1 m3/s共5组不同流量条件进行试验。模型试验中，溢洪道泄流量用矩形量水堰量测，沿程水压力采用测压管量测，流速用直读式旋桨流速仪和毕托管测量，水面线用测针测量，对某一点的流速(或水面高度)分别测量3次，流速值(或水面高度)取3次测量的平均值。

3 试验结果

3.1 过堰流态

利用测针测出不同来流量条件下溢洪道堰体前后各观测断面的水面线分布情况，如图4所示(来流量383.1 m3/s)。图4(a)中，由于选用的堰体布置方式没有设置扭面等改变原渠道断面的过渡段，上下游及控制段边墙自然过渡，堰前水流较为平顺，堰面没有出现明显的水面波动；图4(b)中，堰面下两侧边墙处水深明显高于底板中部，且断面水面波形呈对称分布，在底板中心处水面开始隆起；图4(c)中，断面水面呈现出中心凸起、两侧平缓的形态，底板中心处的水冠较为明显。溢洪道整体过堰流态如图5所示。图5中，下游泄槽段内出现一定的菱形波，在堰面下0+033.4断面两侧边墙首先发生，两侧波形分布对称，并向溢洪道中心发展直至相互顶冲和碰撞，顶冲点处水面隆起、水冠较高，顶冲点后菱形波呈折冲式向溢洪道两边发展，直至碰到两侧边墙后又折向溢洪道中心。可见，菱形波会对下游泄槽段边墙设计高度造成影响。

图4 流量383.1 m3/s时堰体前后水面线观测断面水深分布图

图5溢洪道水流过堰流态

3.2 过流流速分布

利用直读式旋桨流速仪和毕托管测量断面0+009.00和0+055.60在各流量工况下的水流流速分布，测量结果见表1。由表1可知，各断面平均水流流速与流量大致呈正相关关系；两个断面间水流水头损失百分比为1.64%～17.85%，反映出流量越低时，当水流经过堰体时水头损失越大；当流量为232.1 m3/s时，水头损失百分比最小，为1.64%，表明当溢洪道达到某一流量，水流经过驼峰堰时水头损失可降至最低，泄流能力提升。

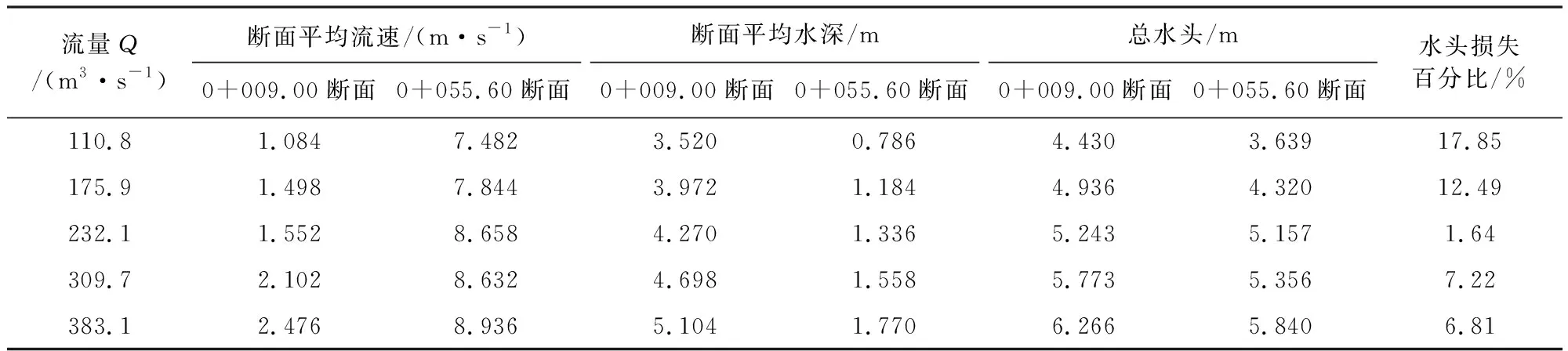
表1 各流量工况下测量断面平均流速测量结果

图6为各流量工况下堰体前后断面的流速分布图。由图可知，堰前断面流速分布较均匀，与流量间正相关关系较明显；堰后断面流速分布表现出明显的差异性，呈现出“W”型，断面中心处流速相对于两侧明显较小，当流量为232.1 m3/s时，断面中心处流速与平均流速差值最大，表明受堰后菱形波的影响，断面上各点流速与流量间无明显的相关性。

3.3 堰面压强分布

本次模型试验采用测压管量测堰面及前后底板上的水压力，沿中心线共设置了17个测点，水压力测点布置见图7。共测试了5组不同过流条件下的沿程水压力。结果表明：在各组试验工况下，相同流量工况下堰前底板水压力值沿程变化不明显，但堰面水压力值呈现出明显的“V”形变化，即先下降至最低点后再快速上升，堰面水压力最低值约4.32 kPa～5.49 kPa，出现在堰顶偏下部位；堰后底板沿程水压力值在大流量情况下变化明显，当流量小于175.9 m3/s时，底板沿程水压力值变化不明显，当流量大于175.9 m3/s时，底板沿程水压力值增幅随流量的增加呈正相关关系，当流量为383.1 m3/s时，增幅达39.4%。总体来看，堰面曲线合理，满足泄洪运行要求。

图6各流量工况下堰体前后断面流速分布图(m/s)

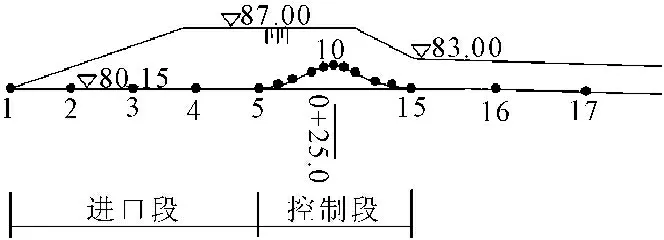
图7溢洪道堰面及前后底板水压力测点布置图

图8为各流量工况下堰面及前后底板中心线处的水压力曲线图，由图8可知：总体各压力曲线近似平行，随着来流量的增加，各测点处的水压力也随之增加，尤其进口段及堰后底板处各测点水压力值变化明显，与来流量相关性较好；但堰顶附近水压力值随流量变化不大。在同一流量条件下，进口段及堰后底板处各测点压力变化曲线较为平缓，这是由于进口段及堰后泄槽段过流断面均为梯形断面，为明渠均匀流，水头损失相对较小，流态较稳定；当逐渐趋于上堰面反弧段时，过流面积减小，部分势能转化为动能，流速增大，导致堰面水压力减小；在堰顶凸面处，水压力线开始快速下降，到堰顶后某一位置处压强降至最低点，这是由于在该位置液体质点上的惯性离心力与重力合力方向与其流速方向一致，液体质点流速达到最大，导致更多的势能转化为动能，该位置处的压强降至最小；之后下反弧段，随着过流面积的增大，流速减小，压强又开始上升，至泄槽段压强线逐渐趋于水面线；整个堰面压强分布近似为“马鞍形”。本次试验结果显示的压强规律完全符合急变流动水压强分布规律，与其它研究成果文献[13-15]基本是一致的。

图8各流量工况下堰面及前后底板中心线处的水压力曲线图

4 泄流能力计算

4.1 泄流宽度

对于驼峰堰自由泄流的下泄流量，设计采用了下列公式进行计算：

(2)

式中：Q为泄流量，m3/s；m0为驼峰堰自由泄流的流量系数；H0为堰上水头，H0=上游库水位-堰顶高程，m；B为溢流宽度；g为重力加速度，g=9.81 m/s2。

在堰顶宽度相同、同一水位条件下，梯形明渠中驼峰堰的泄流量大于矩形明渠中驼峰堰的泄流量[2]。由公式(2)可得公式(3)：

(3)

其中：BH0为过流断面的面积，由此可知，堰体下泄流量主要与过流断面成正比，即可得公式(4)：

(4)

其中：S为堰顶处梯形断面过水面积。

在本试验中公式(4)可化为公式(5)：

(5)

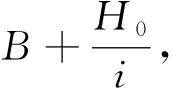
4.2 流量系数

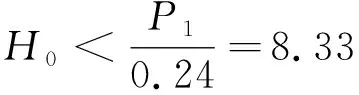
因此，本模型中，流量系数可表示为：

(6)

由公式(6)可知，流量系数与堰上水头呈指数关系。

4.3 泄流量

利用公式(5)和公式(6)得出不同库水位条件下的计算流量Q计，计算结果见表2及图9。

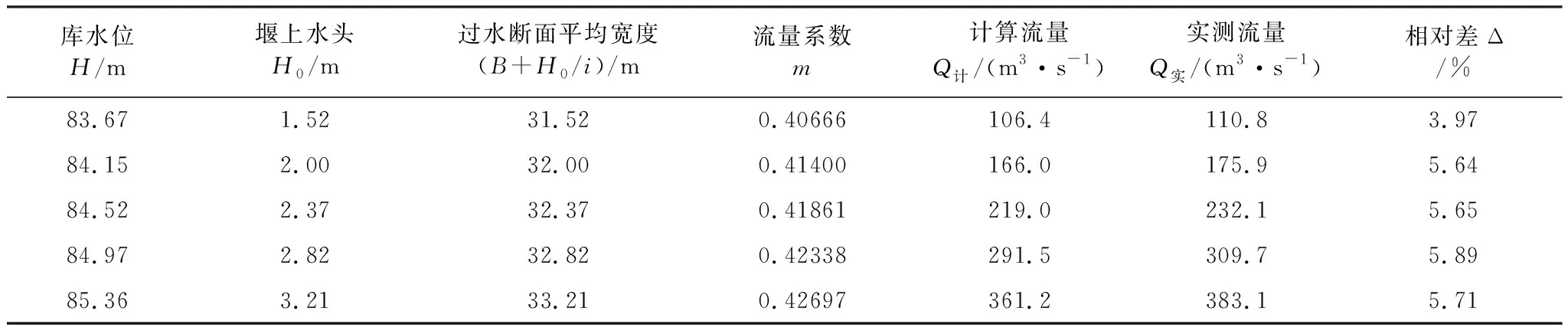
表2 不同库水位条件下计算流量与实测流量对比表

注：本试验中，驼峰堰两侧边墙坡比i=1。

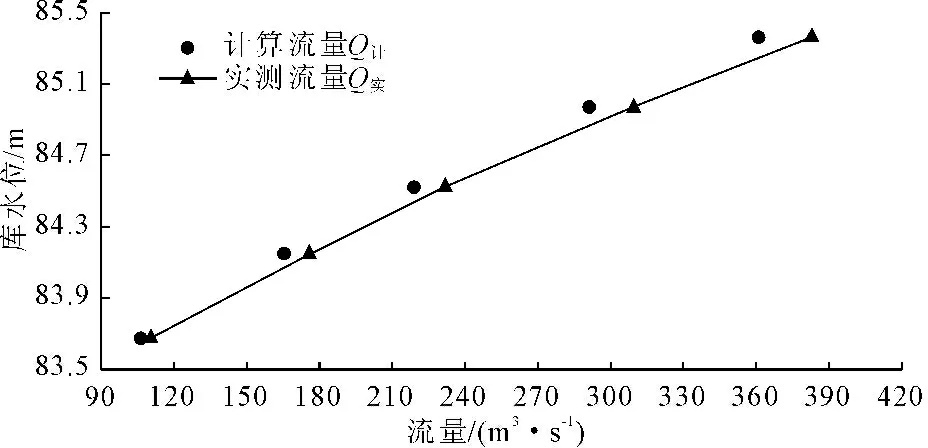
图9驼峰堰泄流量与库水位关系曲线

与规范[16]中的经验公式计算结果比较，实测流量比计算流量大3.97%～5.89%，表明在实际工作中以经验公式计算梯形明渠中驼峰堰的泄流量基本满足要求，并留有一定的超泄能力。

5 结 语

(1) 将驼峰堰直接修建在军民水库梯形明渠中，具有堰面流态好、堰顶过流断面大，泄流能力强，堰前不易淤积等优点。但下游泄槽段内出现一定的菱形波，在下游泄槽段边墙高度设计时应考虑菱形波造成的影响。

(2) 堰面及上下游水压力分布基本呈现“马鞍形”，符合驼峰堰压强分布一般规律，满足溢流堰设计要求。

(3) 泄流能力计算时，驼峰堰溢流宽度需采用堰顶平均过水宽度；流量系数与堰上水头呈指数关系；在没有实测资料的情况下，采用溢洪道设计规范中的经验公式计算流量基本能够满足要求，并留有一定的超泄能力。

(4) 堰下泄槽内出现的菱形波，会对下游泄槽内局部水面产生一定影响，应通过进一步试验，确定边墙高度。