基于SPEI的中国百年干旱时空变化特征分析

刘 晓 勇

(咸阳市水利局， 陕西 咸阳 712000)

干旱是一种持续时间长、影响范围广、发生频率高的自然灾害[1]。近年来，随着气候变化、人类活动的加剧，干旱发生的强度和频率都有增加的趋势，频发性、高强度的干旱天气加剧了区域水资源供需矛盾，造成水质恶化，作物减产，生态恶化等一系列连锁灾害[2]。世界上诸多国家和地区都曾受干旱的侵扰，严重影响了这些国家地区的自然生态环境和人类生活[3]。由于季风途径和强弱的年际变化大，长期以来我国大范围的干旱频繁发生[4]，据水利部报道，在1990年—2007年间，平均每两年我国就会发生一次极端干旱事件，平均每次干旱引起的粮食减产达392亿kg，占国民经济生产总值的1.47%，因干旱引起的经济损失达700多亿元[5]。进入21世纪以来，由于气候变化等的影响，中国面临的干旱风险更加严峻，因此，深入理解干旱时空变化特征对于未来干旱发生风险管理及水资源合理配置具有重要意义。

以往关于干旱的研究多是基于站点进行，通过游程理论识别干旱特征(历时、烈度、烈度峰值)，利用Copula函数分析多种干旱特征的联合分布特性及变量间相依性[6]。Copula函数是Sklar[7]提出的一种联接函数，Copula函数可以通过联接不同的边缘分布，获得多变量联合概率特征，在国内外干旱分析中得到了广泛应用[1，8-13]。Copula函数的广泛应用表明其能够对多个特征变量进行更优的联合拟合，对干旱发生特点进行更精确地分析[11]。但是，基于站点的干旱分析方法可以为小范围的干旱风险管理提供准确信息，但是在大范围的干旱管理与风险评估中的适用性较差[14]。因此，需要在大范围研究区域干旱时空发生特点，探索区域干旱发生风险。

本文以整个中国为研究对象，基于1901年—2015年的月SPEI数据，通过空间干旱特征识别方法识别干旱面积与干旱烈度，分析中国百年干旱的时空发生特点，并利用Copula函数探究干旱面积与干旱烈度相依性，并绘制干旱烈度-面积-频率曲线。

1 研究资料与方法

1.1 研究数据

本文的研究区域为整个中国地区，数据为1901年—2015年共115年的月SPEI指数监测干旱，SPEI指数是Vicente-Serrano等[15]在标准化降水指数(SPI)的基础上通过引入潜在蒸散量构建的，融合了SPI和帕尔默干旱指数(PDSI)的优点，SPEI用水分亏缺量和持续时间2个因素来描述干旱，可以很好地表示干旱的程度[16]。SPEI数据来源于网站(http://spei.csic.es/index.html)，空间分辨率为0.5°。

1.2 干旱特征识别

本研究所用干旱特征包括：

(1) 干旱影响面积(At)：At表示时刻t区域干旱面积(ηspei<ηspeithr)所占比例，公式为：

(1)

式中：I[.]为逻辑指标函数；ηspei i,t为第i个栅格t时期的SPEI值；ηspeithr为干旱阈值，本文取为0；ai表示第i个栅格的面积值；Np为栅格总数。

(2)干旱烈度(St)：

(2)

式中：Nct表示t时期干旱栅格总数。

1.3 基于Copula的联合概率函数

Copula函数的理论基础是Sklar定理，假设Fxy是二维联合概率分布函数，其边缘分布为Fx与Fy，存在一个Copula函数使得：

Fxy=C(Fx，Fy)=C(u，v)

(3)

如果Fx与Fy是连续的，则C是唯一的，否则C由ranFx×ranFy唯一确定[17]。

Copula函数有不同的函数族，本文选用以下6种Copula函数作为备选Copula：Gumbel Copula、Clayton Copula、Frank Copula、Joe Copula、Galambos Copula和Normal Copula。

1.4 基于Copula的条件重现期

干旱烈度关于干旱影响面积的条件重现期可以表示为：

(4)

式中：μ=N/n，N为数据系列长度(年)；n为干旱发生次数；CS|A=a表示给定干旱面积a时，干旱烈度S的累积概率函数。联合Copula的条件分布根据下式计算：

(5)

2 结果与分析

2.1 干旱特征分析

首先利用0.5°分辨率的SPEI数据计算出了中国地区的干旱烈度(S)与干旱面积(A)(见图1)。中国地区1901年—2015年干旱烈度与干旱面积总体呈增加趋势，干旱烈度与干旱面积的变化趋势一致，为探索干旱烈度与干旱面积的关系，首先对两者进行边缘分布拟合，选择最优拟合函数。

2.2 干旱特征的边缘分布优选及相依性度量

选择7种常用分布函数(Gamma，Weibull，Normal，Lognormal，Logistics，Loglogistics，Gev)对干旱烈度与干旱面积进行拟合，选择KS检验与AD检验两种检验方法对不同分布进行拟合优度检验，检验结果如表1所示，对于干旱面积(A)，Weibull分布的拟合效果最好，对于干旱烈度(S)，Gev分布的拟合效果最好。

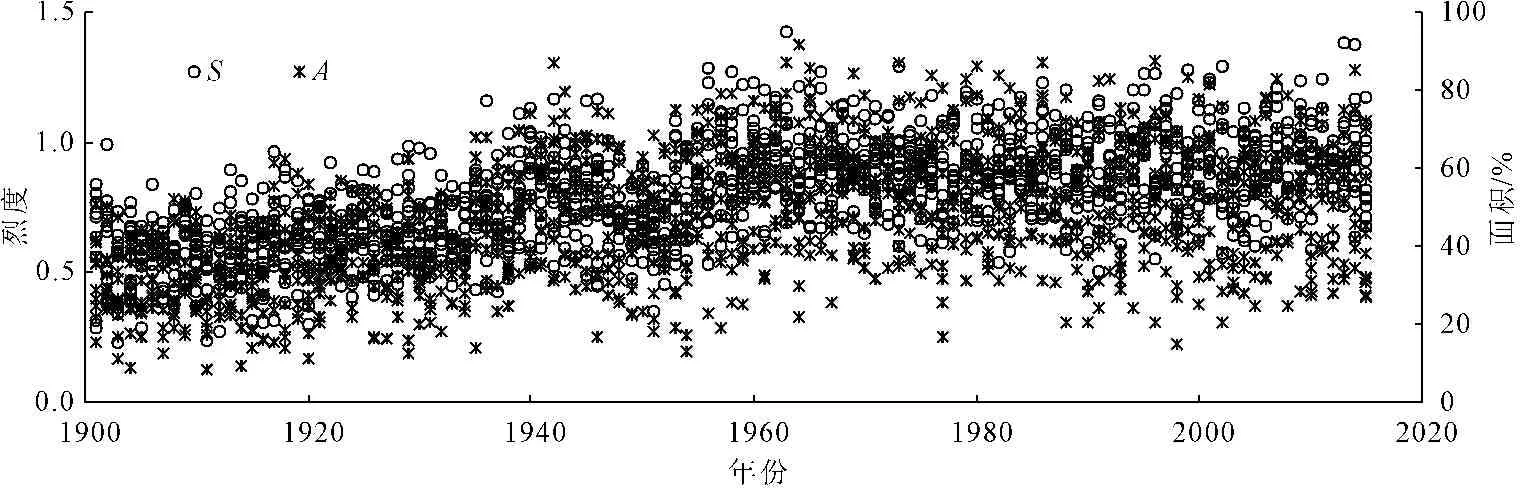
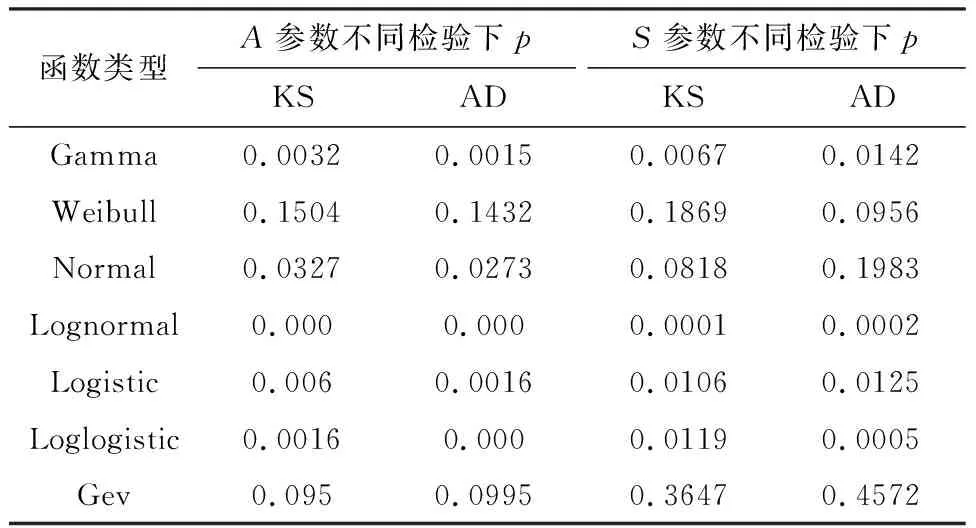
图1 1900年—2015年干旱烈度/面积变化

图2中给出了Weibull分布拟合干旱面积(A)和Gev分布拟合干旱烈度(S)的概率密度图、累积概率分布图、P-P图及Q-Q图，结果显示，Weibull分布对于A的拟合良好，Gev分布对S的拟合良好，因此，选择Weibull分布为A的边缘分布，Gev分布为S的边缘分布。

在利用Copula函数对变量进行联合之前，首先需要对变量的相依性进行度量，判定变量与变量之间是否存在强相依关系。分别绘制了干旱面积与干旱烈度的分级排序散点图、Chi图和Kendall图(见图3)，结果显示，干旱面积与干旱烈度之间存在较强的相依性，可以利用Copula函数联结。

2.3 基于Copula的干旱特征分析

文中选择了6种Copula函数(Clayton，Gumbel，Frank，Joe，Galambos，Normal)对干旱面积与干旱烈度进行联结，并与经验联合概率进行对比，选择CM(Sn)检验方法对拟合结果进行检验，结果表明(表2)Normal Copula分布的拟合效果最好。

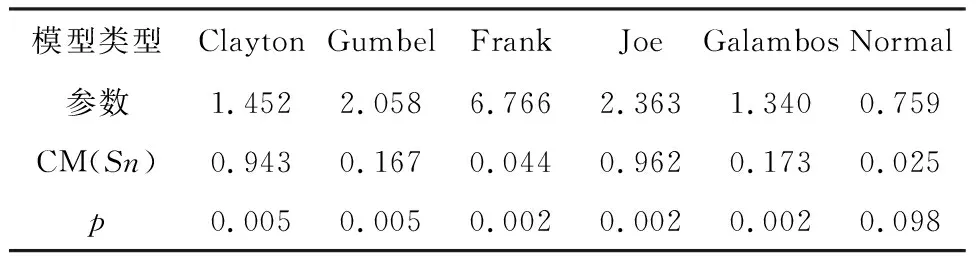
表2 不同类型Copula模型参数估计及拟合优度检验

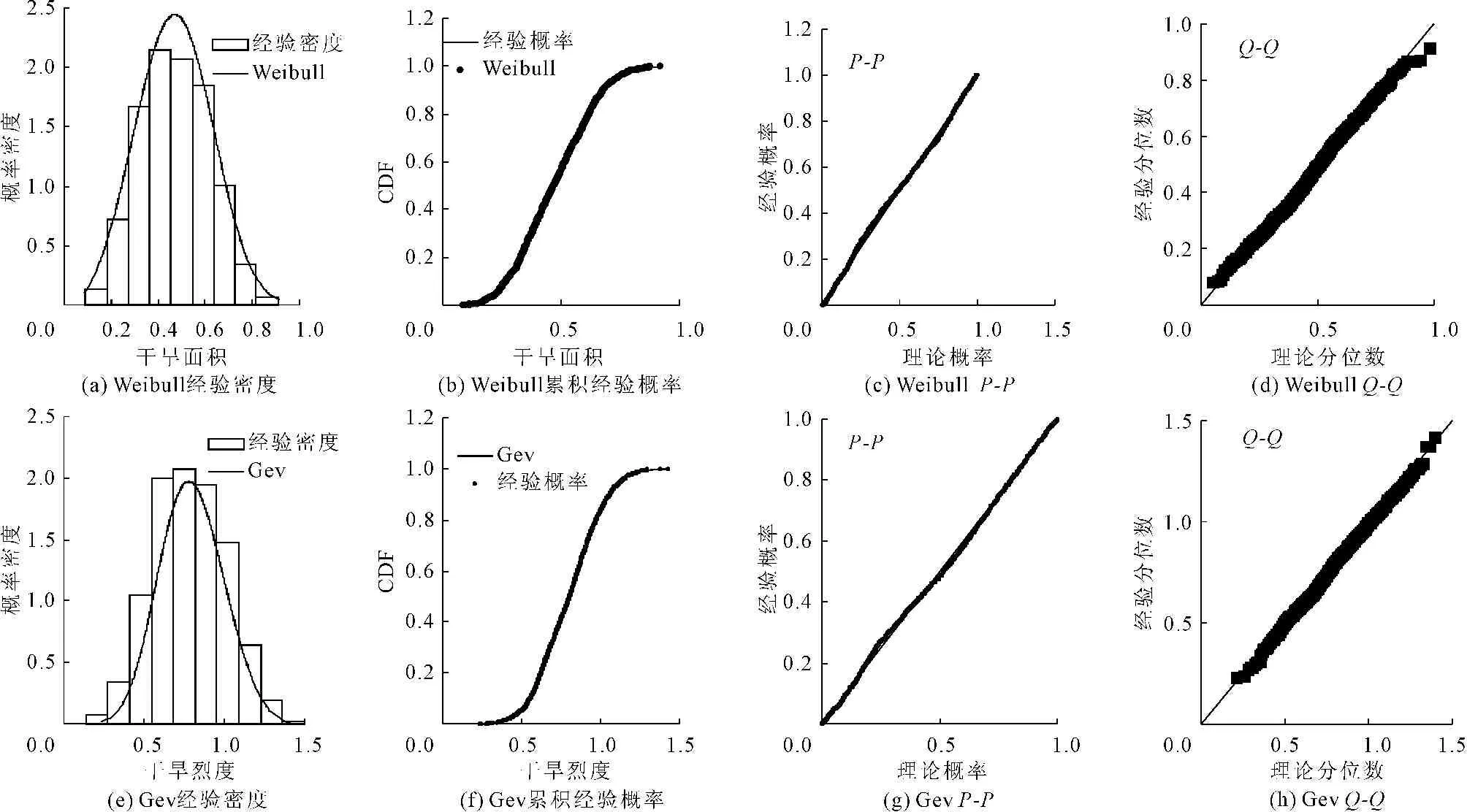
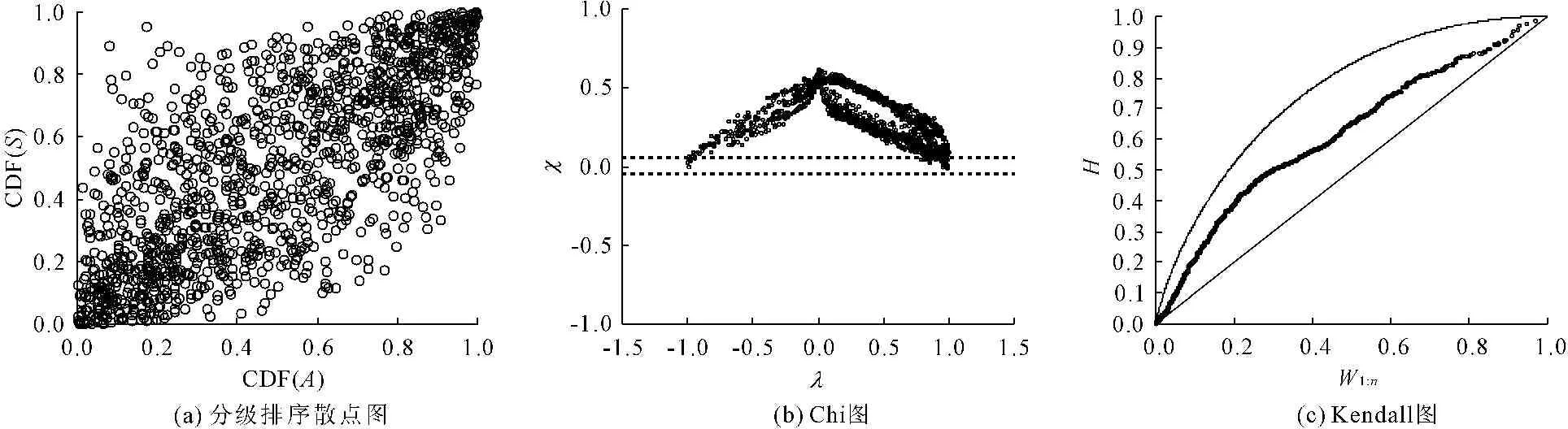
图2 基于最优分布函数的干旱面积(A)、干旱烈度(S)PDF、CDF、P-P、Q-Q图

图3干旱面积与干旱烈度的相依性度量

为了比较不同Copula函数的拟合效果，分别绘制了基于不同Copula模型的干旱面积和干旱烈度实测值与随机生成值的累积概率散点图(见图4)及基于不同Copula模型的干旱面积和干旱烈度实测值与随机生成值散点图，结果表明Normal Copula函数的模型效果最好，实测值与随机生成值的匹配效果最优，因此，选择Normal Copula函数作为干旱面积与干旱烈度的联接函数。

图4基于不同Copula模型的干旱面积和干旱烈度实测(黑色)与生成(灰色)累积概率散点图

2.4 干旱烈度-面积-频率曲线

干旱烈度-面积-频率曲线表示给定干旱面积重现期的条件下干旱烈度的重现期，表示干旱面积对干旱烈度的影响程度，计算公式为：

(6)

(7)

式中u1=FA(a),u2=FS(s)，Φ表示正态变换，具体过程可参见宋松柏教授的Copulas函数及其在水文中的应用[18]。对应不同重现期的干旱烈度-面积-频率曲线如图5所示，随着干旱烈度的增加，干旱面积也呈增加趋势。根据干旱烈度-面积-频率曲线图可以识别给定干旱面积重现期条件下干旱烈度的发生频率。对于区域干旱特征分析及水资源管理具有重要的科学意义。

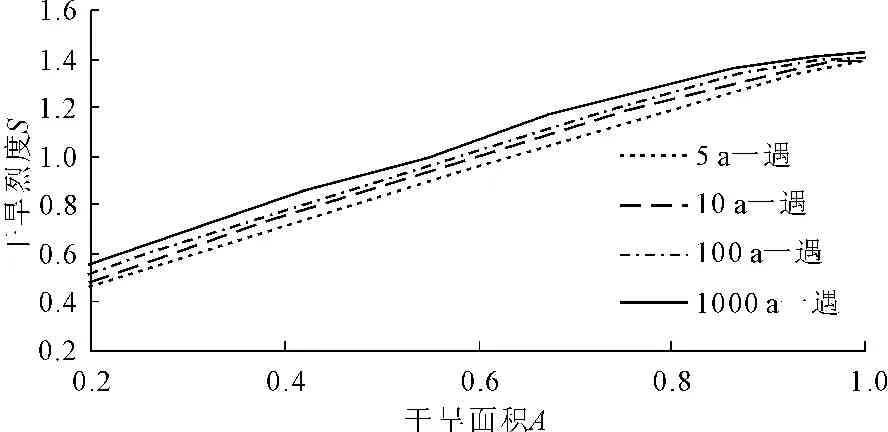
图5不同重现期对应的面积-烈度-概率曲线

3 结 论

正确识别区域干旱特征对于水资源管理具有重要的指导意义。本文基于中国地区1901—2015年的月SPEI数据对干旱烈度与干旱面积进行识别，并优选出最适宜边缘分布函数，进而优选Copula函数对干旱面积与干旱烈度进行联合，最后绘制干旱烈度-面积-频率曲线，对干旱特征进行分析，得到以下主要结论：

(1) 1901年—2015年间，中国地区基于SPEI指数识别的干旱烈度与干旱面积总体呈增加趋势，且两者趋势一致，具有较强的相依性。

(2) 干旱面积最适宜的边缘分布函数为Weibull分布，干旱烈度最适宜的分布函数为Gev分布，干旱面积与干旱烈度的最适宜联接函数为Normal Copula函数。

(3) 根据干旱烈度-面积-频率曲线，随着干旱烈度的增加，干旱面积也呈增加趋势，根据干旱烈度-面积-频率曲线图可以识别给定干旱面积重现期条件下干旱烈度的发生频率，对于区域干旱特征分析及水资源管理具有重要的科学意义。