微分方程和差分方程指数型二分性条件的等价
邹长武, 张章学
(1. 福州大学数学与计算机科学学院,福建 福州 350116;2. 中国科学院信息工程研究所,中国科学院网络测评技术重点实验室,北京 100093)
0 引言
指数型二分性在常微分方程中应用广泛,最早由林振声[1]提出,后来在Copple等[2]的工作下,有了系统的发展. 随着研究的深入,除了常微分方程外,指数型二分性还在差分方程[4],时滞微分方程等方面有着广泛的应用[3-5]. 成为研究有界解、周期解、概周期解及其拓扑线性化的强有力的工具.
对于不同类型的方程,指数型二分性的定义一般有些区别. 即使对于相同的方程,也可能有不同的定义,而不同的指数型二分性定义又有所联系. 近年来,不同的指数型二分性条件之间的关系,引起了许多学者的关注. 例如,对于带有扩展类型分段常参数的微分方程 (DEPCAGs),x′(t)=A(t)x(t)+A0(t)x(γ(t))[6-8]和带有分段常参数的微分方程 (DEPCAs)x′(t)=A(t)x(t)+A0(t)x([t])[9,10]的指数型二分性各种不同定义之间的研究受到许多学者关注[11-12]. 对于DEPCAGs和DEPCAs指数型二分性的定义的不同,归结原因,是因为有些定义用连续微分方程指数型二分性的定义,而有些用差分方程的指数型二分性的定义,另一些用连续微分方程和差分方程指数型二分性的定义相结合的方法来定义. 所以有必要讨论最一般的连续微分方程和差分方程的指数型二分性的定义之间的联系.
1 主要结论
对于一般的线性微分方程
x′=A(t)x(t)
(1)
其中:x(t)是r维向量,A(t)是r阶方阵. 假设系统(1)的基本解矩阵为X(t), 则系统(1)在上满足指数型二分性[1]是指:存在常数K>0,α>0及其投影矩阵P使得下列条件成立, 条件(I)
注1投影矩阵P满足:Pk=P,(I-P)k=(I-P),其中k是正整数.
对于一般的线性差分系统
y(n+1)=B(n)y(n)
(2)
其中:n∈,y(n)是r维向量,B(n) 是r阶方阵. 假设系统(2)的基本解矩阵为Y(t),称系统(2)在上满足参数为(P,K,α)的指数型二分性[4]是指: 存在常数K>0,α>0及其投影矩阵P使得
|Y(n)PY-1(m)|≤Ke-α(n-m)(n≥m)
|Y(n)PY-1(m)|≤Ke-α(m-n)(m>n)
其中:m,n∈.

|X(n)PX-1(m)|≤Ke-α(n-m)(n≥m)
|X(n)PX-1(m)|≤Ke-α(m-n)(m>n)
之间的关系. 为此,本研究引入有界增长的概念.
定义1若对任意h∈,|A(t)|dt≤M,则称系统(1)有界增长[13].
注2若A(t)有界,则必有界增长,反之不然.
下面,给出本研究的第一个结论.
定理1若系统(1)有界增长,则条件
1) |X(t)PX-1(s)|≤Ke-α(t-s)(t≥s)
2) |X(t)(I-P)X-1(s)|≤Ke-α(s-t)(t 等价于 下面将有界增长概念稍作修改. 由此定义,得到本研究的另一个结论. 定理2条件 ① |X(t)PX-1(s)|≤Ke-α(t-s)(t≥s) ② |X(t)(I-P)X-1(s)|≤Ke-α(s-t)(t≤s) ③ 系统(1)基解有界增长 等价于 Ⅲ) 系统(1)基解带投影P负向有界增长,且带投影I-P正向有界增长 为了证明本研究的结论,先给出一个引理. 引理1设系统(1)基解为X(t),若系统(1)有界增长,则存在常数l>0,对任意t,s∈, 只要|t-s|≤1,必有 |X(t)X-1(s)|≤l 证明 设x(t,s,x0)为系统(1)的解,则有 所以 再由Gronwall不等式,可得 当 |s-t|≤1 时,有 |x(t,s,x0)|≤|x0|eM 即 从而有 注3由此引理可知定义2中的基解有界增长x0的定义是很自然的. 为了便于阅读,再列出本研究要证明的结论. 定理3若系统(1)有界增长,则条件 1) |X(t)PX-1(s)|≤Ke-α(t-s)(t≥s) 2) |X(t)(I-P)X-1(s)|≤Ke-α(s-t)(t 等价于 ii) |X(m)(I-P)X-1(n)|≤Ke-α(m-n)(m≥n) 证明 必要性. 必要性显然成立,证明过程省略. 充分性. 任给s n≤s 从而 所以条件1)成立,条件2)类似可证. 定理证毕. 定理4条件 ① |X(t)PX-1(s)|≤Ke-α(t-s)(t≥s) ② |X(t)(I-P)X-1(s)|≤Ke-α(s-t)(t≤s) ③ 系统(1)基解有界增长 等价于 Ⅲ) 系统(1)基解带投影P负向有界增长,且带投影I-P正向有界增长 证明 必要性. 由定理1可推得条件Ⅰ),Ⅱ)成立,下面证明Ⅲ). 由恒等式X(t)X-1(s)=X(t)(P+I-P)X-1(s),可知 当-1 |X(t)PX-1(s)|≤|X(t)X-1(s)|+|X(t)(I-P)X-1(s)| 由于系统(1)有界增长,所以有 |X(t)X-1(s)|≤l 又由条件②知 |X(t)(I-P)X-1(s)|≤K 当 -1≤s-t≤0时, |X(t)(I-P)X-1(s)|≤|X(t)X-1(s)|+|X(t)PX-1(s)|≤l+K 必要性证毕,下证充分性. 充分性. 由定理1,只要证明系统(1)有界增长即可. 当 -1≤t-s≤0 时, 设整数n满足n≤s 由条件Ⅲ)可得, |X(t)PX-1(s)|≤l |X(t)(I-P)X-1(n-1)|≤l 和 |X(n+1)(I-P)X-1(s)|≤l 又由条件Ⅱ)知, 因此 当-1≤s-t≤0时,设整数m满足m≤t 由条件Ⅲ),可得 |X(t)(I-P)X-1(s)|≤l |X(t)PX-1(m+1)|≤l 和 |X(m-1)PX-1(s)|≤l 又由条件Ⅱ)知 因此 从而系统(1)有界增长,定理证毕.


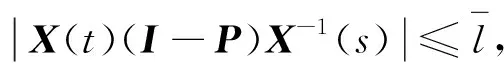


2 结论的证明