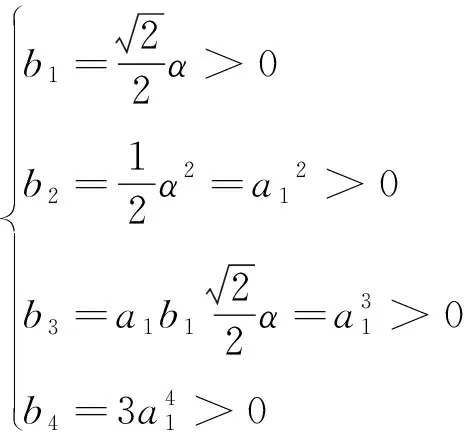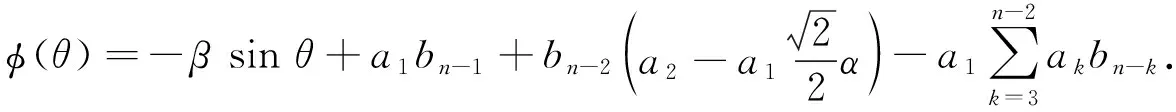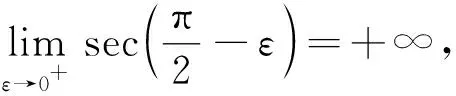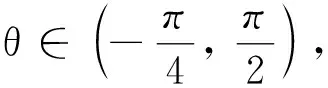一类非零元个数最少的谱任意Ray 模式

邓将武, 刘 月

(福州大学数学与计算机科学学院,福建 福州 350116)

0 引言

一个n阶矩阵A=(ajk)是Ray模式矩阵,是指A的元素ajk∈{eiθ|0≤θ<2π}∪{0},i2=-1.A的定性矩阵类为

QR(A)={B=(bjk)∈Mn(C)|bjk=rjkajk,rjk∈+, 1≤j,k≤n}

Ray模式是符号模式[1]的一种复推广.

n阶Ray模式矩阵A称为谱任意的,是指对任意的首一n次复系数多项式f(x),存在一个复矩阵B∈QR(A),使得B的特征多项式为f(x).

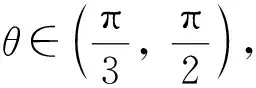
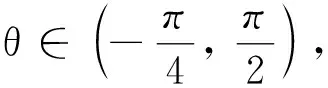
本研究将运用幂零-中心化方法研究Ray模式S的谱任意性. Ray模式A′和Ray模式S的形式如下

1 幂零-中心化方法

对于Ray模式A,若存在复矩阵B∈QR(A)和正整数k,使得Bk=0但Bk-1≠0,则B为幂零矩阵,从而A蕴含幂零,称k为复矩阵B的幂零指数.

设Ray模式P=(pjk)和Ray模式A=(ajk),如果对于ajk≠0, 都有ajk=pjk,则称Ray模式P=(pjk)是Ray模式A=(ajk)的母模式.

设A为n×n矩阵,若C(A)={B|AB|=BA,B∈Mn(C)} ,则称C(A)为A的中心,且B为A的中心化子矩阵.

下面的定理介绍了幂零-中心化方法.

定理1[9](幂零-中心化方法) 设A是一个n阶Ray模式,B∈QR(A)是一个幂零指数为n的幂零复矩阵. 如果在B的中心里满足条件C∘AT=0(这里C∘AT表示矩阵C和AT的Hadamard乘积)的矩阵C只有零矩阵,则Ray模式矩阵A及其每一个母模式都是谱任意的.

根据定理1,在第2节中,首先找到一个幂零矩阵B∈QR(S),其次证明满足条件C∈C(B)且C∘ST=0的矩阵C只能为零矩阵,进而证明Ray模式矩阵S是谱任意的.

2 主要结果

设n是一个正整数且n≥5. 考虑如下n×n复矩阵

(1)

这里α>0,β>0. 如果aj>0(1≤j≤n-1)和bj>0(1≤j≤n-1),则B∈QR(S). 记

(2)

其中

fk=fk(α,a1,a2, …,an-1;b1,b2, …,bn-1,β),gk=gk(α,a1,a2, …,an-1;b1,b2, …,bn-1,β)

分别表示λn-k系数αk的实部和虚部,k=1, 2, …,n.

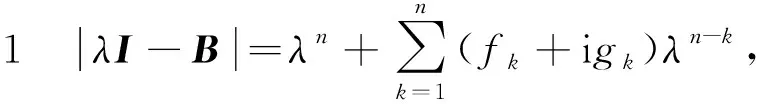
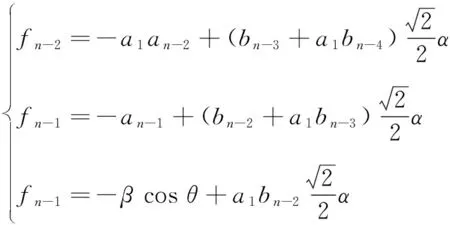
以及

证明 对于2≤t≤n-2,记

由式子(2)可得

将|λI-B|按第一列展开可得

因此,可以得到

所以引理得证.

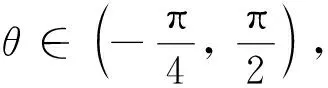
证明 设B有形式(1),若aj>0(1≤j≤n-1)和bj>0(1≤j≤n-1),使得在fk=0(1≤k≤n)和gk=0(1≤k≤n)则B∈QR(S)是幂零矩阵. 在式子(1)中,假设fk=0(1≤k≤n)和gk=0(1≤k≤n),由引理1, 则有

布局需要以物料流动为导向，Milk-run需要定制布局，避免长距离、大面积和较长的交付周期。在理想的情况下，每个加工零件都直接用于下一个生产工序，机器之间的运输步骤减少能简化Milk-run系统的使用流程。同时布局必须考虑道路容量，车道需要满足火车的正常行驶和转弯需求。用于存放物料的货架应放置在生产单元附近并与路线相邻，这样就可以让Milk-run司机轻松地把它们装满。除了Milk-run火车本身，提供生产的物料也需要空间。仓库需要提供足够的面积存放火车等运输设备。

以及

取0

下证

对j进行归纳. 当j=5时，

假设aj>0和bj>0对于任意的j

且

由归纳可知,当5≤j≤n-3时,aj>0和bj>0. 因为

从而an-2>0,bn-2>0,所以an-1>0,bn-1>0.

接着考虑

因此

由C∘ST=0,可知c1, i=0(i=1, 2,n-1,n),ci-1, i=0(i=2, …,n-1),c2, i=0(i=1, …,n-2,n),ci, n=0(i=3, 4, …,n-2,n-1),cn-1, n-1=0. 又因为CB=BC,CB的第一行和BC的第一行相等,则

所以,c1, i=0(i=3, …,n-3,n-2),c2, n-1=0. 则c1, i=0(i=1, 2, …,n-1,n),c2, i=0(i=1, 2, …,n-1,n). 依次类推可得,ci, j=0(i=3, …,n;j=1, 2, …,n). 因此,C=0. 由引理1可知,Ray模式矩阵S是谱任意的. 从而定理得证.