CeFe2−xInx合金磁性研究与CeFe1.95In0.05合金磁相变临界参数分析∗

陈湘 赵明骅

1)(内江师范学院物理与电子信息工程学院,内江 641112)2)(The Ames Laboratory,U.S.Department of Energy,Iowa State University,Ames,Iowa 50011-3020,U.S.A.)

(2018年4月26日收到；2018年8月3日收到修改稿)

1 引 言

在绝大多数Laves相结构的REFe2(RE=稀土)合金中,稀土的4f电子和铁的3d电子分别属于局域电子和巡游电子.在4f-3d,3d-3d,4f-4f相互作用中,3d-3d的相互作用明显强于其他形式的相互作用,这导致多数REFe2为伴随高居里温度(TC)的铁磁态[1,2],如545 K(YFe2),525 K(PrFe2),305 K(NdFe2),425 K(SmFe2),782 K(GdFe2),694 K(TbFe2),638 K(DyFe2),593 K(HoFe2),574 K(ErFe2)等.但对于CeFe2合金而言,Eriksson等[3]研究表明Ce原子的4f电子不同于其他REFe2合金中的RE元素4f局域电子,而属于巡游电子,这导致很多有趣的磁现象.首先,CeFe2合金展现出低居里温度(≈230 K)和低饱和磁化强度Ms(≈2.3µB/f.u.)[3,4].其次,CeFe2合金不完全处于铁磁态,在低温状态下(6100 K),合金中出现反铁磁态(AFM)振荡[5],即铁磁态与反铁磁态共存,Ce-4f电子和Fe-3d电子轨道杂化被认为是造成这种现象的主要原因[3].中子衍射表明Ce 4f-Fe 3d轨道杂化效应使得自旋波强度降低,并导致合金出现AFM自旋振荡[6,7].当通过CeFe2合金中参杂而使电子浓度微量改变时,AFM可以从振荡状态过度到稳定状态.目前的研究表明,用其他稀土替代CeFe2合金中的Ce时,并不能使Ce 4f-Fe 3d相互作用加强,而出现低温反铁磁态稳定的现象；相反会使Fe 3d-Fe 3d相互作用加强,导致合金居里温度升高.如用5%和10%的Gd以及10%的Ho替代Ce时,合金的居里温度可提高至267—318 K[8],且饱和磁化强度Ms下降. 在(Ce1−yScy)Fe2(y 60.10)合金中,随Sc含量增加,TC从230 K(CeFe2)可增加至270 K(Ce0.90Sc0.10Fe2),低温Ms也逐渐增加,合金中仍能观察到AFM应振荡现象[9].但用少量的Al,Mn,Co,Ni,Ru,Ir,Re,Os元素替代Fe原子时,会使合金中Ce 4f-Fe 3d轨道杂化相互作用强于Fe 3d-Fe 3d的交换相互作用,低温下反铁磁态得到稳定,即低温时合金处于反铁磁状态[9−21].如在Ce(Fe1−xCox)2(0.05 6x6 0.1)合金中,其磁状态为反铁磁(低温)-铁磁态(低于TC)-顺磁态(高于TC),且随Co含量增加AFM-FM相变温度单调增加,而FM-PM相变温度降低[9].Ce(Fe0.96Al0.04)2合金的TC和TAFM-FM分别为200 K和95 K[11].在Ce(Fe,5%Ir)2和 Ce(Fe,7%Ru)2合金中,TC分别为185 K和165 K,TAFM-FM分别为135 K和125 K[16]. 另外,Haldar等[22−24]研究发现超过某一临界量的IIIA族元素Ga和IV族元素Si替代CeFe2中的Fe时,也观察到现象低温反铁磁态稳定的现象,Ce(Fe1−xGax/Si)2合金的临界值分别为x=0.025和x=0.05.

为进一步探究其他IIIA族元素替代CeFe2合金中的Fe时,对Fe 3d-Fe 3d和Ce 4f-Fe 3d相互作用的影响而导致的磁性宏观特性,本文研究了CeFe2−xInx合金的相结构、磁性.同时,采用标度临界参数(β,γ,δ,n)讨论了CeFe1.95In0.05合金的磁相互作用.

2 实验方法

实验方法1:原材料Ce,Fe和In的纯度分别为99.98 wt.%,99.95 wt.%,99.999 wt.%,按照考虑Ce质量的3%为熔损进行CeFe2−xInx合金(x=0,0.05,0.15,0.2)化学配比.通过充有高纯氩气的钨极非自耗电弧炉进行样品制备(反复熔炼6次).经熔炼所得的铸锭样品密封于高真石英管内置于管式炉中进行热处理,其热处理机制工艺是:在600◦C保温2 d,700◦C保温5 d,800◦C保温7 d,850◦C保温2 d,然后冰水淬火.利用DX-2600射线衍射仪对制备好的样品进行结构分析.

实验方法2:采用美国Ames实验室材料制备中心制备的稀土Ce(99.98 wt.%)、购自于Alfa Aeser商业级Fe(99.95 wt.%)和In(99.999 wt.%),考虑按照正常化学计量比Ce质量的3%为熔损进行CeFe2−xInx合金(x=0,0.05)化学配比.通过充有高纯氩气的钨极非自耗电弧炉进行样品制备(反复熔炼6次).将样品用金属Ta片包裹后,密封于充有高纯氩气的小石英管进行热处理.经熔炼所得的铸锭样品密封于高真石英管内置于管式炉中进行热处理,其热处理机制工艺是:在600◦C保温2d,700◦C保温5 d,800◦C保温7 d,850◦C 保温2 d,然后冰水淬火(不破碎石英管).X射线衍射通过Philips X’Pert Pro衍射仪(铜靶)完成.用超导量子干涉磁性测量仪(SQUID,MPMS XL,USA)对其进行磁性测量,温度范围为2—300 K,磁场范围为0—7 T.

3 结果与讨论

3.1 相与结构

图1是通过实验方法1所制备的CeFe2−xInx样品的X射线粉末衍射谱.可以看出虽然合金的主相均为Laves结构CeFe2相,但随着In含量的增加,合金中杂相含量增加,这表明In替代Fe形成CeFe2−xInx替代式固溶体的固溶度是非常有限的.图2是通过实验方法2制备的CeFe2和CeFe1.95In0.05样品的衍射图谱,通过Rietveld精修对样品的相纯度和相结构进行分析.CeFe2合金为立方结构MgCu2型单相,而在CeFe1.95In0.05样品衍射谱中的2θ=30.75◦和35.80◦处有两个杂相的衍射峰,但衍射强度很低,这表明该杂相的含量百分比是很低的.在其他Ce(Fe1−xMx)2合金中,如Ce(Fe0.95Co0.05)2[9],Ce(Fe0.095Ga0.05)2[22],Ce(Fe0.0975Ga0.025)2[22],Ce(Fe0.095Si0.05)2[24]等的衍射谱中,也能观察到2θ=30.75◦的衍射峰.因为In的原子半径比Fe的大,因此CeFe1.95In0.05的原子半径(a=7.3035(2)Å)比CeFe2的值(a=7.2939(3)Å)更大. 在CeFe1.95In0.05合金晶胞中各原子的占位信息列于表1中,Fe和In占据16 d位置的比例分别为97.438%和2.434%,这同其分子式是符合的.

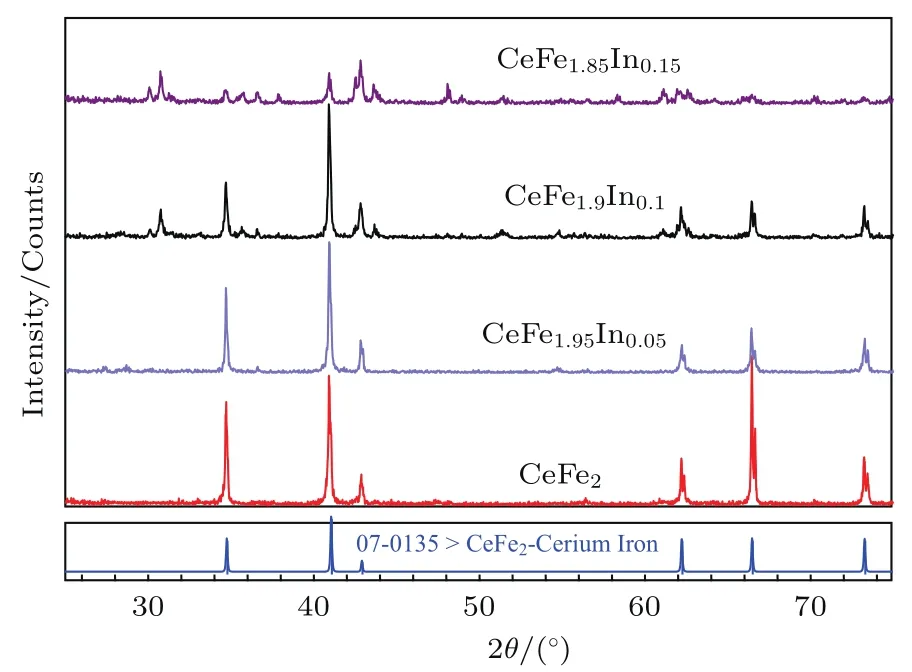
图1 CeFe2−xInx(x=0,0.05,0.1,0.15)样品的X射线粉末衍射谱Fig.1. The X-ray powder diffraction pattern of CeFe2−xInx(x=0,0.05,0.1,0.15)samples.

图2 CeFe2和CeFe1.95In0.05样品的室温粉末衍射图谱Fig.2.The X-ray powder diffraction pattern of CeFe1.95In0.05phase.

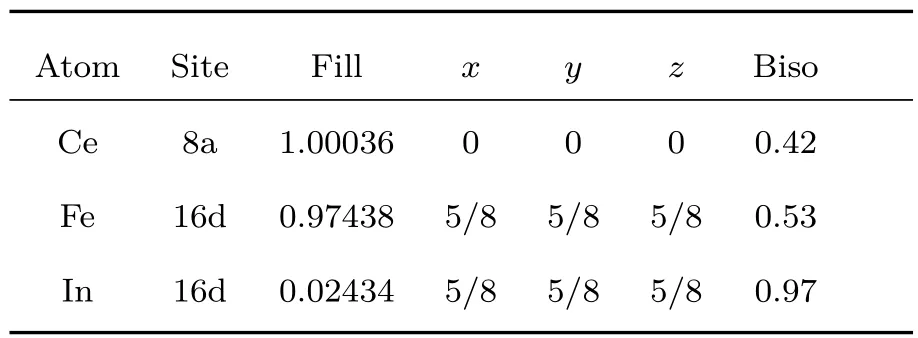
表1 CeFe1.95In0.05合金的原子占位表Table 1.The lattice parameters of CeFe1.95In0.05alloy.

3.2 磁 性

图3(a)分别是CeFe1.95In0.05合金先零场冷却然后在加场升温过程中(ZFC)、加场冷却过程中(FC)、加场冷却后在升温过程中(FCW)测试的磁化强度(M)随温度(T)的变化(M-T)曲线.由于CeFe1.95In0.05合金中杂相含量很低,因此本文在讨论磁性相关参数时没有考虑其他磁性离子引起的误差.从图中可以看出,在0.01 T磁场下,类似于CeFe2合金中的反铁磁振荡现象在80 K仍然能被观察到,如图3(a)插图所示.从图3(b)可以观察到CeFe1.95In0.05合金中80 K以下ZFC于FCW之间的磁化强度差值比CeFe2的更大,这说明反铁磁态更加稳定,即合金中Ce 4f-Fe 3d的杂化作用加强.Ce(Fe1−xGax)2与Ce(Fe1−xSix)2合金的晶格常数随Ga和Si量的增加而增大,如当x=0,0.01,0.025,0.05时,Ce(Fe1−xGax)2的晶格常数分别为7.3018(3),7.3059(3),7.3090(3),7.3097(5)Å[22]；在Ce(Fe1−xSix)2合金中, 当x= 0.01,0.025,0.05时,晶格常数分别为7.3020(3),7.3033(4),7.3054(3) Å[24]. 基于Ce(Fe1−xGax/Six)2合金中x分别达到0.025和0.05后,AFM才能在低温时处于稳定状态,可以认为Ce(Fe1−xTx)2(T=Ga,Si)中晶胞膨胀至某一临界值后,低温下合金的反铁磁态才能稳定存在.相比于CeFe2合金,Ce(Fe0.975In0.025)2的晶格膨胀率为1.00131(5)%,这比Ce(Fe0.975Ga0.025)2和Ce(Fe0.95Si0.05)2的1.00098(6)%与1.00049(3)%稍微大一些,由此推断Ce(Fe0.975In0.025)2中的反铁磁态应该比同等参杂量的Ce(Fe0.975Ga0.025)2更稳定.但从实验结果来看,虽然在CeFe2的中用2.5 at.%的In替代Fe,可以使得Ce 4f-Fe 3d的杂化作用得到加强,但未能到达某一临界值或强于Fe 3d-Fe 3d相互作用,而出现低温反铁磁稳定态.这也表明Ce(Fe1−xTx)2合金中低温反铁磁态的稳定存在不仅取决于晶格膨胀,还与磁电子浓度的变化有关.从图3(a)中可以看出,随着磁场的增加,低温反铁磁态会逐渐转变为铁磁态,当外场达到10 kOe时,在居里温度以下只有铁磁态存在.通过dM/dT图确定的CeFe1.95In0.05合金铁磁-顺磁相变居里温度为230.2 K,比CeFe2合金相应的相变温度227.0 K更高.这表明参杂In对决定居里温度的Fe 3d-Fe 3d磁相互作用的影响很小.

对CeFe1.95In0.05合金而言,在低场100 Oe下,顺磁区域内的磁化曲线遵循居里-外斯定律顺磁外斯温度θ 为229.8 K,居里常P数C=4.98.根据

图4(a)是温度为2 K时,CeFe1.95In0.05和CeFe2合金的磁化强度随外磁场(H)变化回滞曲线(M-H曲线).为保证在测量前合金处于完全退磁状态,样品先被加热至室温,然后零场冷却至2 K,再进行测量.从图中可以看出,两个合金的磁滞非常小,这表明磁畴钉扎效应引起的矫顽力非常弱.通过M-H曲线外推得到的CeFe1.95In0.05合金零场下的自发饱和磁矩为2.77µB/f.u,这比CeFe2的2.56µB/f.u要大,这种现象在(Ce1−yScy)Fe2(y60.10)也被观察到[9].这表明在CeFe2合金中Fe原子位置参杂In可以增加合金中Fe原子的有效铁磁磁矩. 图4(b)为CeFe1.95In0.05和CeFe2合金在227 K的M-H曲线.在60 kOe外磁场下,磁滞几乎为零,两种合金的饱和磁矩分别为1.61和1.50µB/f.u.

图3 (a)CeFe1.95In0.05合金不同磁场下采用ZFC,FC,FCW测量方法测量的M-T曲线,插图为0.1 kOe磁场下2—230 K的局部放大图；(b)0.1 kOe磁场下,CeFe2和CeFe1.95In0.05合金不同磁场下采用ZFC,FC测量方法测量的M-T曲线Fig.3.(a)The temperature dependence of the magnetization of CeFe1.95In0.05by measured ZFC,FC and FCW methods in different applied magnetic field,the inset shows magnetic field dependence of magnetization in 0.1 kOefield from 2 to 230 K；(b)the temperature dependence of the ZFC heating and field-cooled cooling(FC)magnetization of CeFe1.95In0.05and CeFe2in applied magnetic field of 0.1 kOe.

图4 不同温度下CeFe1.95In0.05和CeFe2合金的等温磁化曲线 (a)2 K,−60—60 kOe；(b)277 K,0—60 kOeFig.4.Magnetizations of CeFe1.95In0.05and CeFe2as a function of applied magnetic field(a)from−60 to 60 kOe at 2 K and(b)from 0 to 60 kOe at 277 K.

图5 (a)0—50 k1Oe外磁场范围内,CeFe1.95In0.05合金从203—260 K的等温磁化曲线；(b)用β=0.5和γ=1.0通过vs.(H/M)γ构建的Arrott图Fig.5.(a)The isothermal magnetization of CeFe1.95In0.05measured in applied magnetic fields from 0 to 50 kOefrom 203 to 260 K；(b)the Arrott plots vs.(H/Mderived from the isothermal magnetization data withβ=0.5 and γ=1.0.

通常情况下,磁相变类型可以通过基于长程相互作用于的平均场理论而构建的Arrott模型(图)来判断.图5(a)和图5(b)是CeFe1.95In0.05在203—260 K温度范围内的等温磁化曲线(M-H)和对应的Arrott图(M2-H/M).从图5(b)中可以看出,不同温度的Arrott曲线的斜率为正,这表明该合金中居里温度处的PM-FM相变为二级相变[25].同时,在高场下合金的Arrott曲线具有很好直线关系,但居里温度处的高场线性部分Arrott曲线反向延长线偏离原点较多,这表明平均场理论不能完全描述CeFe1.95In0.05合金的磁相变行为[26].

4 标度理论

为进一步探究CeFe1.95In0.05合金居里温度附近磁相变的相关特性,如磁相互作用类型等,我们采用标度临界参数分析合金的磁相变行为.

目前除分子平均场理论模型(β=0.5,γ=1.0)外,还有3种其他模型描述铁磁-顺磁二级连续磁相变临界行为,分别是3D-Ising模型(β=0.325,γ=1.241),3D-Heisenberg模型 (β=0.365,γ=1.336)和临界平均场模型(β=0.25,γ=1.241),其中β和γ分别是与自发磁化强度随温度变化和磁化率随温度变化有关的临界指数.因为高场下Arrott直线为一系列平行直线,因此上述各种模型中不同温度下Arrott图直线部分的相对斜率(RS=S(T)/S(TC))应该接近于1[26].图6是基于CeFe1.95In0.05等温磁化曲线(图5(a))的上述四模型的Arrott图中高场线性部分的相对斜率随温度的变化图.相比而言,短程相互作用的3D-Ising模型更接近于理想值1.这表明3D-Ising模型可能是决定CeFe1.95In0.05合金磁相变临界参数的最佳模型.

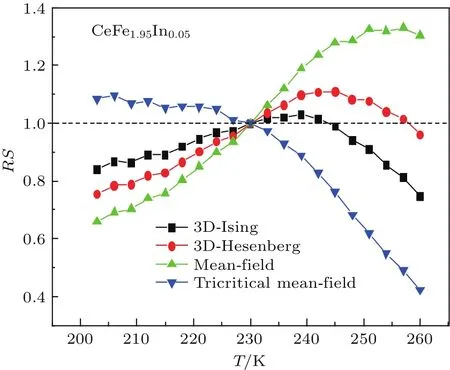
图6 四种模型参数构建的Arrott图线性部分相对斜率随温度的变化Fig.6. The relative slope(RS)of 3D-Ising,3DHesnberg,mean-field and tricritical mean-field models as a function temperature.

为获得CeFe1.95In0.05合金较为精确的相变临界参数,首先采用基于Arrott-Noakes状态方程的Modified Arrott Plots(MAP)来进行分析相关数据.在标度理论中,自发饱和磁化强度和磁化率的倒数满足如下关系[27],即Arrott-Noakes状态方程:

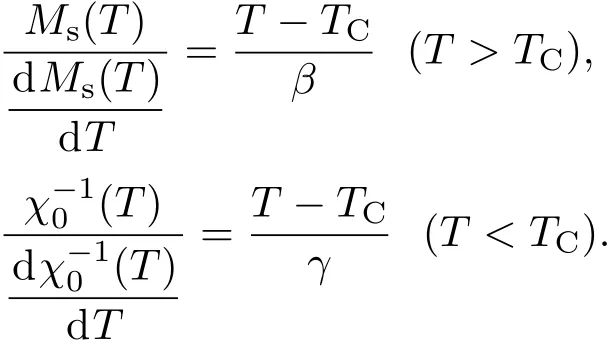
其中ε=(T−TC)/TC.因为在图5(b)中的高场部分呈现很好的直线关系,因此采用线性延长高场直线部分,该线同纵坐标(M2)与横坐标((H/M)1/γ)的交点分别为相应温度的MT)和χ−1(T)[26],图7(a)为Ms(T)-T与χ−1(T)-T关系图.通过上述方程,对图7(a)进行多次拟合,直至得到稳定的临界参数β与γ,其值分别为β=0.3212(8),γ=0.9357(9).图7(b)是采用这组参数构建新的Arrott图(MAP),从图中可以清楚地看到高场下各直线相互平行,且居里温度处的直线反向延长线几乎过原点.这表明通过MAP得到的临界参数β=0.3212(8),γ=0.9357(9)具有较高的可信度.

为比较不同方法获得的CeFe1.95In0.05合金相变临界参数之间的差异,这里采用了Kouvel-Fisher(KF)关系式来讨论β和γ的值[28]:

采用MAP中同样的方法获得Ms2(T)和χ−1(T)后,通过3点法数值微分,可以得到不同温度点的建的M-(H/M)关系分别对两条实验数据线进行线性拟合,可以得到各自的斜率1/β与1/γ,对应的β=0.3304(1)和γ=0.9249(1),这与采用MAP方法获得β=0.3212(8)和γ=0.9357(9)差异很小.图8(b)是采用这组参数构建的Arrott图.与图7(b)相同,高场下各直线相互平行,且居里温度处的直线反向延长线几乎过原点,表明该组临界参数也具有较高的可信度.

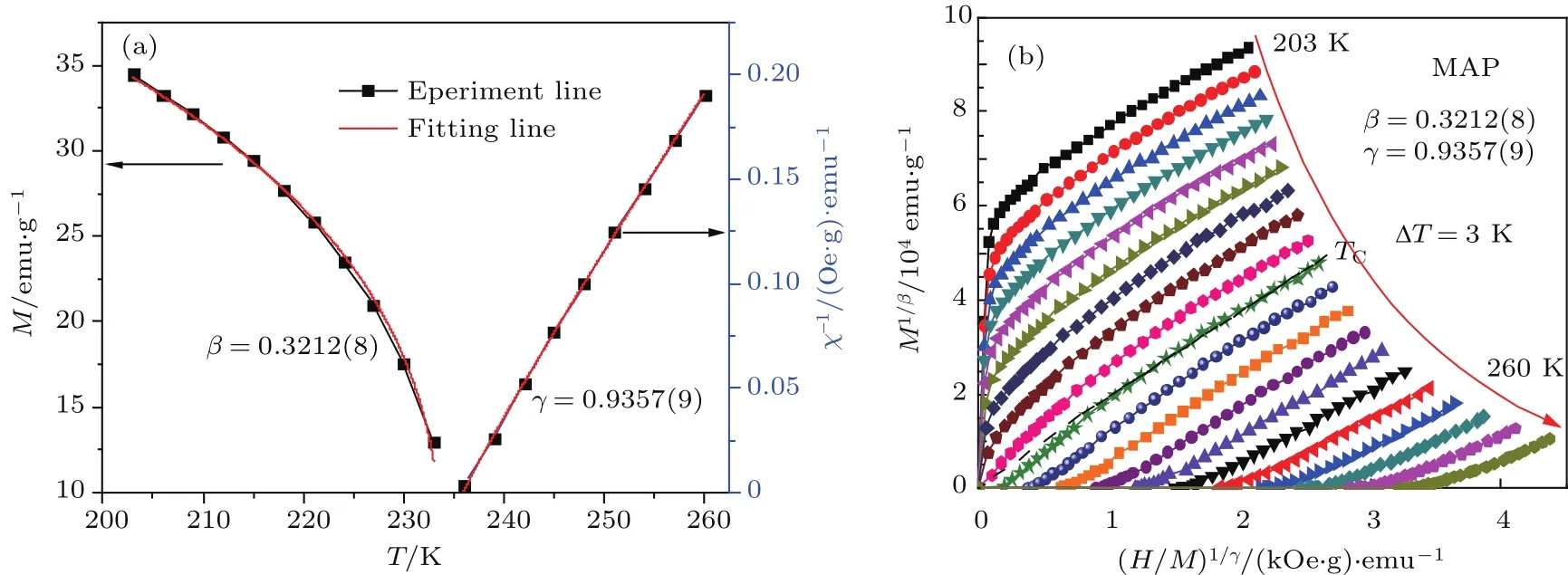
图7 (a)自发饱和磁化强度和磁化率的倒数随温度的变化；(b)用β=0.3212(8)和γ=0.9357(9)构建的MAP图Fig.7.(a)Temperature dependence of the spontaneous magnetization Ms(T)and the inverse initial susceptibility χ−1(T)；(b)modified isothermal Arrott plot -(H/M with β =0.3212(8)and γ =0.9357(9).

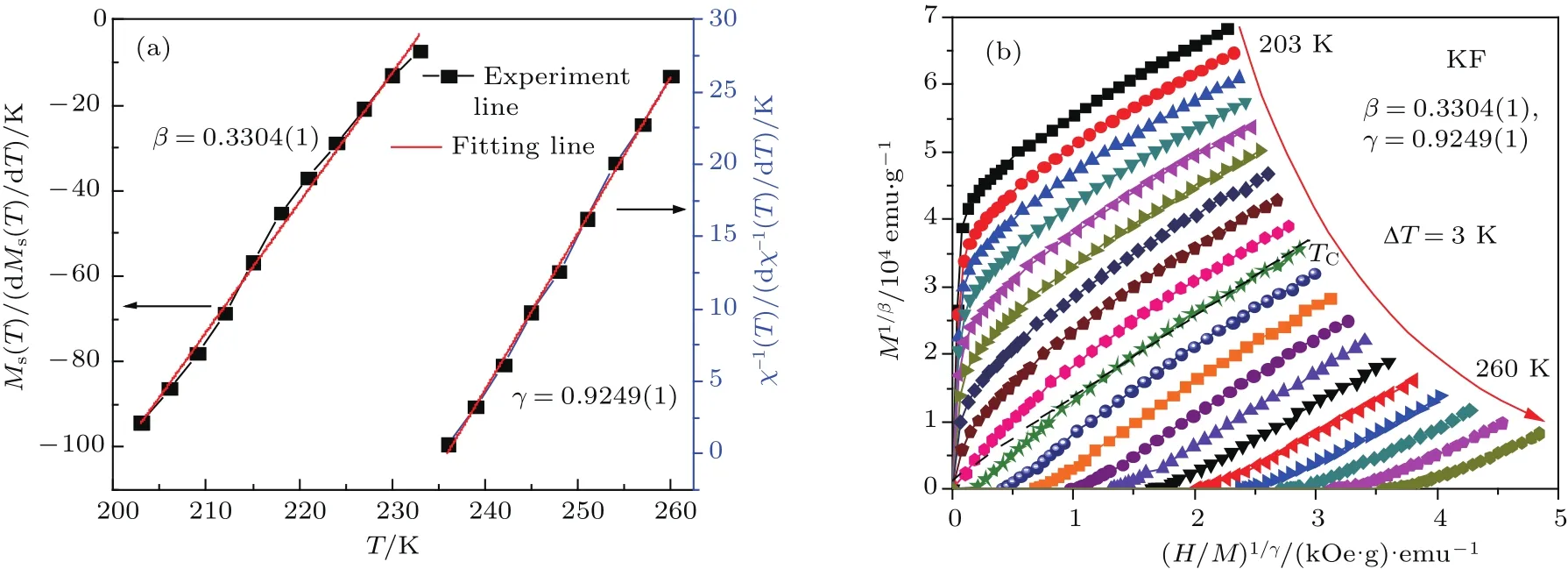
图8

实际上,上述两种方法获得的临界参数的可信度可以通过标度理论来判断. 根据方程[29]:M(H,ε)=|ε|βf± (H/|ε|β+γ),M|ε|−β∝H|ε|−(β+γ), 相应图形中曲线应该以居里温度TC为分界线分成两条空间曲线. 因上述两种方法获得的β和γ差异很小,这里采用它们的平均值,即β=0.3258(4),γ=0.9303(5)来构建M|ε|−β∝ H|ε|−(β+γ)图, 如图9所示. 可以看到曲线以居里温度为中心分成两束曲线,这表明由前面两种方法得到的两个临界参数符合标度标度理论.

图9 CeFe1.95In0.05合金居里温度上下的M|ε|−β∝H|ε|−(β+γ) 图Fig.9.Scaling plots indicating universal curves below and above TCfor the CeFe1.95In0.05.

标度理论的第三个临界参数是δ,它满足Widom标度关系[30]:δ=1+γ/β.根据前面采用MAP和KF方法得到的β和γ,可以计算出δ,其值分别为3.9132(5)和3.7989(4).另外,根据方程MT=TC=D[27],可以从居里温度处的等温磁化曲线得到该参数.图10是CeFe1.95In0.05合金在230 K的log(M)-log(H)关系图,该直线的斜率就是1/δ,线性拟合的结果为δ=3.9810(3).这个值同通过δ=1+γ/β计算的值非常接近.这表明以上各种方法得到临界参数之间具有很好的符合度.

图10 CeFe1.95In0.05合金在230 K的log(H)-log(M)关系图Fig.10.Critical isotherms on log(H)-log(M)scale at TCalong with the fitting curves based on the MT=TC=D

从各种方法获得的临界参数来看,CeFe1.95In0.05合金的β=0.3258(4)与磁性粒子自旋短程相互作用的3D-Ising模型中β值(0.325)非常接近.同时,也可以观察到参数γ=0.9303(5)与3D-Ising模型的标准值1.241之间存在差异,该值更接近分子平均场模型的对应参数值1.0.这表明在3D-Ising模型中仅仅考虑最近邻相互作用,但该模型存在自旋相互作用的非局域效应,即在3D-Ising模型中存在类似于长程相互作用的效应.这种现象也在其他合金系中被观察到,如在具有Tricritical模型的La1−xCaxMnO3(x＞0.4)中的β=0.25±0.03,γ=1.03±0.05与理论值β=0.25,γ=1.241[31]以及具有平均场模型的Mn0.94Ti0.06CoGe中的β=0.61,γ=0.91理论值β=0.25,γ=1.241等[32]之间均存在差异.综合而言,CeFe1.95In0.05合金磁相变临界行为可以用磁性粒子自旋短程相互作用的3D-Ising模型来描述,这与通过各种模型的Arrott直线相对斜率(RS=S(T)/S(TC))分析结果一致,但该合金中类似于长程相互作用对合金的磁性也有一定的影响.可以合理推测亚晶格中Fe-Fe之间的自旋短程相互作用对CeFe1.95In0.05合金3D-Ising模型中各格点磁性粒子的自旋取向起主导作用,合金的净磁矩也来自于这种竞争；而非近邻格点上的磁性粒子自旋扰动作用也应在求解3D-Ising模型精确解时不能忽略.

5 磁热效应和相关临界参数

基于等温磁化曲线,通过麦克斯韦方程可以计算出CeFe1.95In0.05合金的等温磁熵变(∆SM(T)),不同磁场下,其随温度变化的关系如图11所示.该曲线为典型的二级相变材料的∆SM(T)-T曲线,即以居里温度为中心呈对称分布.在1,2,3,4,5 T外场下,CeFe1.95In0.05合金的最大磁熵变值分别为1.13,1.80,2.31,2.74,3.13 J/(kg.K).在5 T外磁场下,Ce0.95Gd0.05Fe2,Ce0.9Gd0.1Fe2,Ce0.9Ho0.1Fe2合金最大磁熵变(∆SMax)分别为2.1,1.6,1.9 J/(kg.K)[8],均比CeFe1.95In0.05合金对应磁场的最大熵变值小,这可能源于CeFe1.95In0.05合金具有更大的磁化强度.通常用相对制冷能力来描述材料的制冷功效,其定义为RCP=−∆SMax×δTFWHM,其中磁熵变半高温度全宽δTFWHM.在1,2,3,4,5 T外场下,CeFe1.95In0.05合金的RCP值分别为 21.6,51.3,81.5,115.1,151.3 J/(kg.K),这也高于Ce1−xRExFe(RE=Gd,Ho)[8]和Ce(Fe1−xSx)2(S=Ga,Al)[21,8]合金的值.

对于二级相变材料而言,居里温度附近的磁熵变和外加磁场之间满足如下关系:|∆SM|∝Hn,指数n同材料的磁状态有关.根据1—5 T磁场下−∆SMax(T)与T对应的值,通过上述公式拟合后,得到n的值为 0.6191(8).根据标度理论,相对制冷量与外加磁场之间满足关系:RCP∝H(1+1/δ).结合同样磁场下RCP与T对应的值,拟合可得δ值为5.0559(1).上述两个参数同3D-Ising模型中的标准值(n=0.569和δ=4.818)比较,可以发现虽然它们之间不完全一致,但差异较小,尤其是标度临界参数δ.这进一步证明CeFe1.95In0.05合金中磁性粒子自旋相互作用符合3D-Ising模型.

对于磁制冷材料而言,基于实验数据的−∆SM(T)-T曲线进行外推后得到的归一化曲线是非常有用的. 由于二级相变磁制冷材料的−∆SM(T)-T曲线以居里温度为中心呈对称分布,其归一化过程为: 首先对不同磁场下的−∆SM(T,H)通过除以对应磁场下的−∆SMax(T,H)来归一化,即

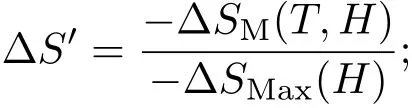
然后对温度进行归一化,并用新的温度坐标表示,其定义为[33]:

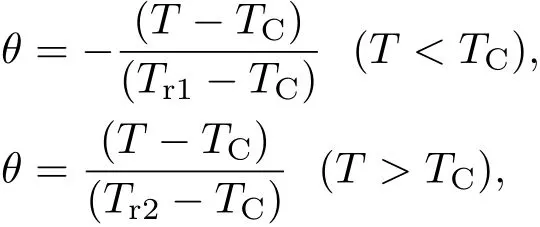
其中Tr1和Tr2分别为−∆SM(T)-T图中居里温度上下磁熵变等于最大熵变的一半所对应的温度.图12(a)为不同磁场下磁熵变的归一化曲线,它们分布于一条归一化曲线的附近,这表明将CeFe1.95In0.05合金的磁相变归于二级相变,并采用上述方法处理相应数据是有效的.

为充分利用归一化曲线对材料的RCP进行评估,还需要找出∆S′与θ的之间的函数关系.由于图12(a)趋于一条归一化曲线,因此可以采用洛伦兹函数进行拟合[34]:

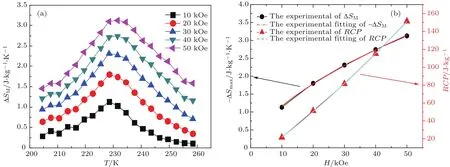
图11 (a)CeFe1.95In0.05合金在不同磁场下的−∆SM-T曲线；(b)RCP-H与−∆SMax-H曲线Fig.11.(a)Temperature dependence of the magnetic entropy change(−∆SM)at different applied magnetic field change intervals for CeFe1.95In0.05；(b)field dependence of the maximum magnetic entropy change and RCP,along with the exponential fitting to determine the values of n and δ,respectively.

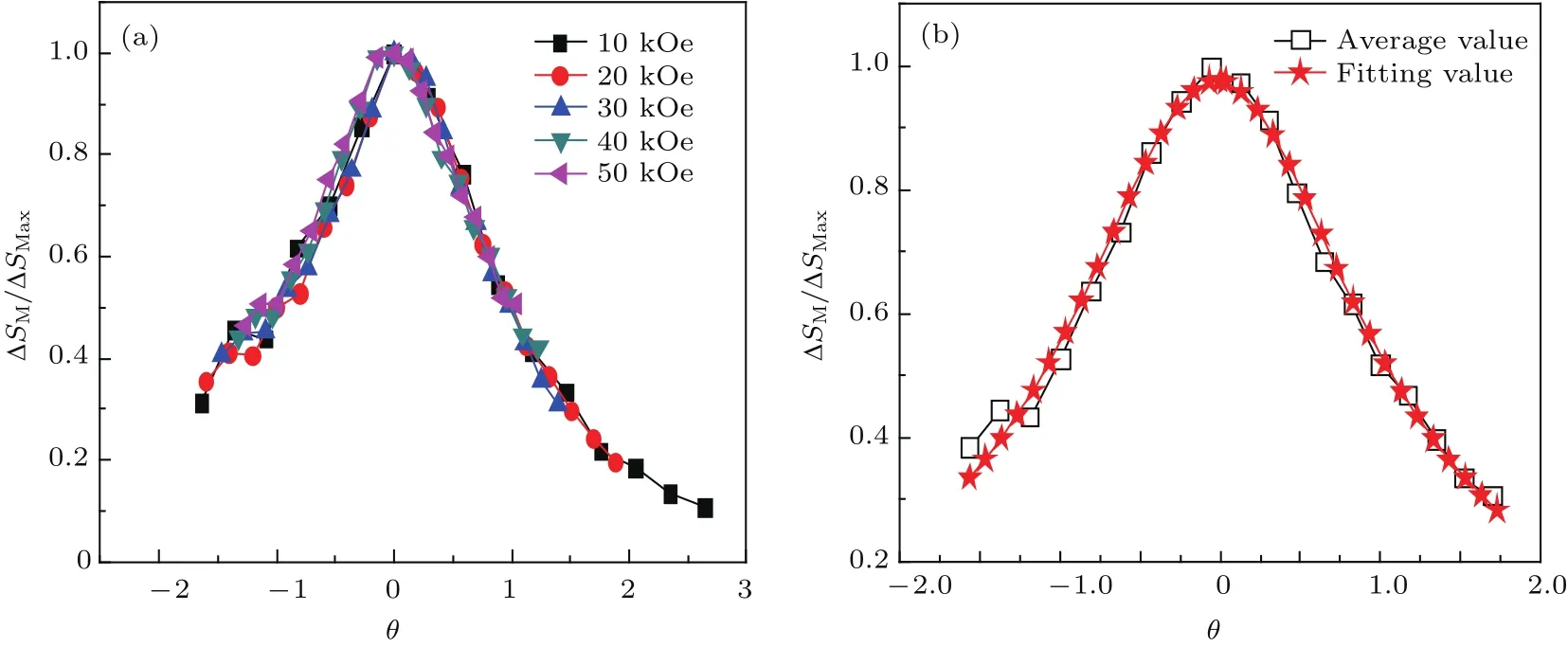
图12 (a)CeFe1.95In0.05合金不同磁场下的磁熵变归一化曲线；(b)CeFe1.95In0.05合金的实验平均归一化曲线与洛伦兹拟合曲线Fig.12.(a)Universal behavior of the scaled entropy change curves of CeFe1.95In0.05in different applied fields；(b)the average of scaled entropy change curve and the fitting curvefitted by Lorentz function.

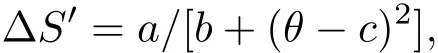
这里a,b,c分别为自由系数.拟合结果为:a=1.2284(8),b=1.2580(4),c=0.0214(1),对应的拟合曲线(图12(b))与不同磁场下归一化磁熵变的平均值曲线几乎重合.因此,只需要给出TC和∆SMax以及两个参考温度Tr1与Tr2就可以求出不同条件合金的磁热性能相关参数.

6 结 论

综上所述,用2.5 at.%的铟替代CeFe2合金中的铁能使Ce-4f电子和Fe-3d电子轨道杂化作用强化,但未能达到某一临界值,因此虽然在CeFe1.95In0.05合金中低温状态下能够观察到比CeFe2合金中更为明显的反铁磁态,但没有观察到如 Ce(Fe1−xGax)2与Ce(Fe1−xSix)2合金体系的低温稳定反铁磁态存在.在CeFe2合金中Fe原子位置参杂In可以增加合金中Fe原子的有效铁磁磁矩,从而可以提高合金的顺磁有效磁矩和铁磁饱和磁矩.CeFe2和CeFe1.95In0.05合金均为典型的二级磁相变材料,采用标度理论的多种方法获得的相变临界参数表明CeFe1.95In0.05合金的磁相互作用可以用3D-Ising模型来进行描述,即该合金中磁相互作用被短距离磁相互作用主宰.

本文的磁性测量工作得到美国Ames实验室的大力支持,感谢Vitalij K.Pecharsky教授和Y.Mudryk教授在论文撰写过程中的帮助.