考虑边聚类与扩散特性的信息传播网络结构优化算法∗

杨李 宋玉蓉2)† 李因伟

1)(南京邮电大学自动化学院,南京 210023)

2)(江苏省物联网智能机器人工程实验室,南京 210023)

3)(南京邮电大学计算机学院,南京 210023)

(2018年3月6日收到；2018年7月18日收到修改稿)

1 引 言

复杂网络研究蓬勃发展二十年以来,诸多研究成果表明网络结构可对网络上的各种动力学行为产生重要影响[1−3],如无标度网络比随机网络和小世界网络同步能力弱[4,5].在病毒传播动力学的研究中,发现无标度网络传播阈值趋向于零[6],网络的高聚类特性对病毒传播具有抑制作用[7].文献[8]在比较病毒传播与信息传播差异时表明,小世界网络具有最有效的信息传播能力.文献[9]通过边重写优化网络的几何连通性来提高网络对抗随机故障和蓄意攻击的能力.文献[10]在费米函数的基础上提出了一种改写网络中的边以促进信息传播的策略.Peng等[11]发现针对网络鲁棒性的优化将降低网络的小世界特性,因此提出了一个启发式算法来获得网络鲁棒性和小世界特性的平衡.文献[5]研究发现,在多层网络的扩散特性是层间相似性的函数,故而通过降低层间相似性达到提高网络扩散性能的目的.信息传播一直是传播动力学中的一个重要研究内容[12].Liu等[13]通过对经典的信息传播事件进行研究,发现信息传播的行为会受到传播中的内在和外在因素影响,通过结合这种内在和外在的因素能够更加有效地促进信息的传播.此外,网络中的病毒传播和信息传播通常具有一定耦合,Zhan等[14]发现当病毒在网络中进行传播时,由病毒传播衍生出的相关信息同样会在网络中进行扩散,反而能够有效地抑制病毒的传播.在该研究的基础上提出了一种信息驱动自适应模型[15],在该模型中个体能够感知病毒传播的信息,可以破坏与感染个体之间的连边.显然,如何优化网络拓扑结构,从而更好地利于有益信息传播、抑制病毒传播是研究者们关注的热点[9−11,15−17].然而在现实生活中,优化网络结构需要考虑的是优化网络的成本与效益.如何用一种对网络结构进行局部性调整的方法以有效地促进信息的扩散也是我们关注的重点.

此外,网络中重要节点对各种网络的传播影响巨大,如病毒营销正是利用了网络中的一些有影响力的节点有效地进行新产品推广.在各种重要节点发现算法中[18],Malliaros等[19]利用K-truss分解算法能够从网络中提取出更精细、更密集的子图,通过该子图来识别网络中的关键节点,相比于K-shell[20]更精确而且时间复杂度也较低.然而,K-truss和K-shell分解都会受到网络中局部聚类结构(即互相连接的假核结构)的影响[21],而这些假核结构里的节点对信息或者病毒的扩散能力通常较弱.文献[22]在定义边的权重时,充分利用了边的扩散特性,极大地提高了识别最有影响力节点的准确性和效率.因此,本文通过在K-truss分解原理的基础上,同时考虑K-truss分解中边的聚类特性和扩散特性,提出一种促进信息传播的网络拓扑优化算法.通过在真实的网络中进行仿真验证,结果表明使用提出的算法对网络结构优化后,可以加快信息在网络中的传播速度,使信息覆盖的范围更广.此外,分析了该算法对网络相关拓扑特性的影响.

本文的内容结构安排如下:第2部分对边的聚类与扩散特性进行介绍；第3部分主要介绍算法的相关理论和算法详细实现过程；第4部分主要进行相关的实验仿真和分析；最后为结论.

2 边的聚类与扩散特性

对于一个给定的无权无向网络 G=(V,E),V代表网络的节点数,E是网络 G中的连边数.eij表示节点 i和节点 j之间的连边,如果节点 i与节点j有连边,则eij等于1；否则eij等于0.节点i的度定义为ki.在K-truss分解中,边eij的支持度[23]表示为

(1)式中,∆ijk表示一个顶点分别为i,j,k的三角形,在图1中,所有与节点i,j构成三角形的另一个节点所构成的节点集用Γ∆ij表示,即图1中由红色虚线包围的浅灰色节点所构成的节点集,则有k∈Γ∆ij；∆G表示网络G中由所有三角形构成的集合；SD(eij)表示在网络中由边 eij构成不同三角形的个数.显然,eij的支持度越高,该边的聚类特性越高,即边的支持度是衡量一条边聚类特性的指标.

本文提出一种衡量边扩散特性的指标,并用DD(eij)表示边eij的扩散特性:

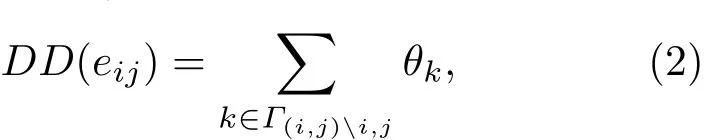
(2)式中,Γ(i,j)表示节点 i和节点 j的邻居节点集,而Γ(i,j)i,j表示节点i和节点j的邻居节点集中除去节点i和节点j后的邻居节点集.当节点k∈Γ(i,j)i,j,并且节点k与节点i和节点j无法构成一个三角形∆ijk时,θk=1；否则,θk=0.例如,在图1中,节点i和节点j的邻居节点集Γ(i,j)i,j所包含的节点个数为4.而在邻居节点中,被红色虚线所标记的深灰色节点无法与节点i和节点j构成三角形.因此,当信息经过边eij对外传播时,信息可以通过这些节点传播到网络中的其他节点,而不是将信息又传播回节点i或节点j从而构成一个信息扩散最小闭环路∆ijk.

同时,用集合Ω(i,j)表示图1中被红色虚线包围的深灰色节点与节点i或节点j之间的连边集合,其可以表示为

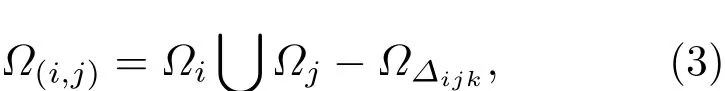
(3)式中,Ωi是节点i与其邻居节点之间的连边所构成的边集合；Ωj是节点j与其邻居节点之间的连边所构成的边集合；Ω∆ijk表示所有与边eij构成的三角形 ∆ijk的边 eik,eij和 ejk所构成的边集合.

通过(1)和(2)式,我们定义一个综合边的聚类和扩散特性的指标SD∇(eij)

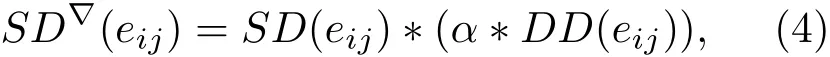
(4)式中,α表示衡量边的聚类特性与扩散特性之间的相对重要程度的比例因子,而比例因子α与综合边的聚类和扩散特性指标SD∇(eij)之间是线性比例关系,计算网络中的所有边的SD∇(eij)指标时,α是相同的,其中α∈(0,1].并且,我们定义的综合指标SD∇(eij)与文献[22]中定义边的权值的原理是相似的.文献[22]指出,一条边的重要性与边的信息或病毒传播过程有关,为此在定义一条有向边的边权时,使用源节点度值乘以目的节点扩散能力来强调边的非对称性.(4)式中SD(eij)与DD(eij)的相乘积形式也正是可以强调:如果网络中的边的聚类特性与扩散特性不平衡,这些边的综合指标SD∇(eij)值就会相对较小.

通过从边的拓扑特征上分析边的聚类特性与扩散特性之间的关系,可以推出:

结合(5)和(6)式可以得到:

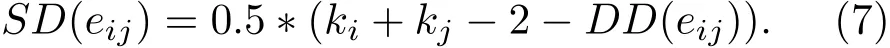
(7)式表示了边的聚类特性与边的扩散特性之间的关系,ki表示节点i的度,kj同理.通过(7)式可以发现,边的聚类特性与边的扩散特性之间存在着互相制约的关系,即若保持一条边的度不变,边的一个特性提高,另一个特性就会相应地下降.结合(4)和(7)式可以将SD∇(eij)指标重写为

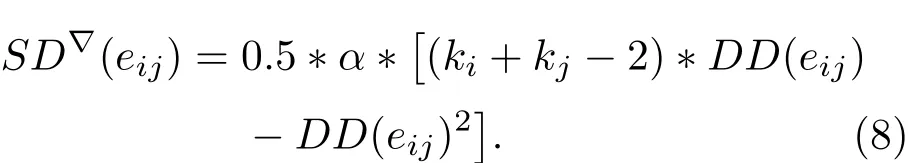
分析(8)式可知,当网络中的一条边eij的扩散特性DD(eij)=0或DD(eij)=ki+kj−2时,都有SD∇(eij)=0.

3 信息传播网络结构优化算法

在信息传播过程中,如果网络中存在互相紧密连接的社团结构,即假核结构,同时该假核结构与网络中其他部分之间的关联较少,会促使信息在网络局部内传播,而不容易扩散到网络的其他部分.同时,一些在网络边缘且不位于假核内的边的扩散性相对较高,而这些边的聚类特性却可能相对较低,也不利于信息的快速传播.

因此,为了能够有效地消除假核结构对信息向外扩散的影响,本文中通过(2)式定义了一种衡量边的扩散特性的指标,并结合(1)式表示的边的聚类特性,定义了一种综合边的聚类特性与扩散特性的指标SD∇(eij)来衡量在信息传播过程中边eij对信息向外快速扩散的能力.根据(7)式发现:网络中的边eij的聚类特性SD(eij)与扩散特性 DD(eij)之间存在着制约关系,即边的聚类特性与扩散特性总和不会变化；两者中有一个特性很高或者很低都会导致SD∇(eij)指标的值相对较小；而对于一条边的聚类特性和扩散特性两者不均衡或者这两个特性相比于网络中的其他边比较低时,都会使得 SD∇(eij)指标的值很小.因此,通过SD∇(eij)的能力强弱来甄选出这些需要优化的边,再结合边eij的聚类特性SD(eij)与扩散特性DD(eij)的相对关系来判定是否需要优化该边以及提出相应的优化策略.详细的算法步骤如下.

步骤1 参数初始化:给定待优化的网络拓扑G、参数α和待优化边数m和优化边比例p,其中m=p∗E,E为网络总边数；根据(1),(2)和(4)式分别计算网络每条边eij对应的聚类特性SD(eij)、扩散特性DD(eij)和综合边的聚类与扩散能力SD∇(eij).

步骤2 将网络中的边按照SD∇(eij)值的大小进行从小到大的进行排序并加入备选边集E′.

步骤3 删边:从E′中选择SD∇(eij)值最小的边 eij,并将该边从备选边集 E′中剔除.比较该边的支持度与扩散性的关系,当α∗DD(eij)＜2∗SD(eij)时,将该边在网络G进行删除,否则在G中保留该边.

步骤4 重复步骤3,直到从网络中删除掉m条边,若满足删除条件的实际边数 m∗＜m,则m=m∗.

步骤5 从边集E′中继续选择SD∇(eij)值最小的边eij,并将该边从集合E′中剔除,判断边eij是否满足条件α∗DD(eij)＞2∗SD(eij).若满足,则执行步骤6,否则继续执行步骤5.

步骤6 增边:根据(3)式从集合 Ω(i,j)中,选择一条支持度最小的边ejk,并连接节点i与节点k,使得增加的边eik与边eij,ejk构成三角形,并更新网络G.

步骤7 重复步骤5和步骤6,直到增加了m条边.

4 仿真分析

4.1 数据源及信息传播模型

在实验仿真中,采用的网络为:1)Dophins网络[24]；2)Polbooks网络[25]；3)Email网络[26]；4)Geom网络[27].真实网络的统计特征如表1,其中N 和E分别是网络的节点数和连边数,⟨k⟩表示网络的平均度,kmax表示最大度,⟨d⟩是网络的平均最短路径长度,C是网络的聚类系数,ΛN是网络邻接矩阵的最大特征值.

实验中采用经典的独立级联模型[28]来描述网络中的信息传播过程.在随机传播模型中,信息的传播被描述成一个随机过程,节点的状态在这个过程中变化.具体而言,每个节点有两个可能的状态:激活态和非激活态.在独立级联模型中,一个节点u一旦在第t步被激活,它在第t+1步去激活它的邻居节点v,即每个被激活的节点只有一次机会去激活它的邻居节点.假设种子节点为S0,节点v被节点u激活的概率为p(u,v).则独立级联模型按照如下的扩散规则进行传播:假设第t−1步处于激活状态的节点集合为 St−1,第 t步处于激活状态的St则在第t+1步时,每个节点u以概率p(u,v)去尝试激活它的邻居节点v.如果成功,则节点v被激活,否则,在接下来的信息传播过程中,节点u不能够再激活其邻居节点.重复这一过程,直到网络中没有具有激活其他节点的活跃节点.而对于激活概率p(u,v),广泛使用1/degree(v)作为节点v被激活的概率[29].

表1 各个真实网络的网络拓扑特征Table 1.Network topology features of each real network.

4.2 信息传播仿真分析

按所提算法对上述4个网络进行边改写,改写边的比例p取0.2,即改写边数m为0.2E.对比网络所有的边在优化前后网络中SD(eij),DD(eij)和SD∇(eij)的变化,结果列于表2.从表2中可以看出,4个网络在优化后,边的支持度即聚类特性下降,扩散特性值增加,综合聚类与扩散特性也呈现下降.这表明,经过提出的算法优化后网络整体的聚类特性和扩散特性的变化具有一定的规律性,且具有相反的变化趋势.同时由于网络整体的综合聚类与扩散特性也呈现出较明显的下降趋势,表明网络的聚类特性相比扩散特性其下降的幅度更大,算法对网络聚类特性的改变效果更明显.

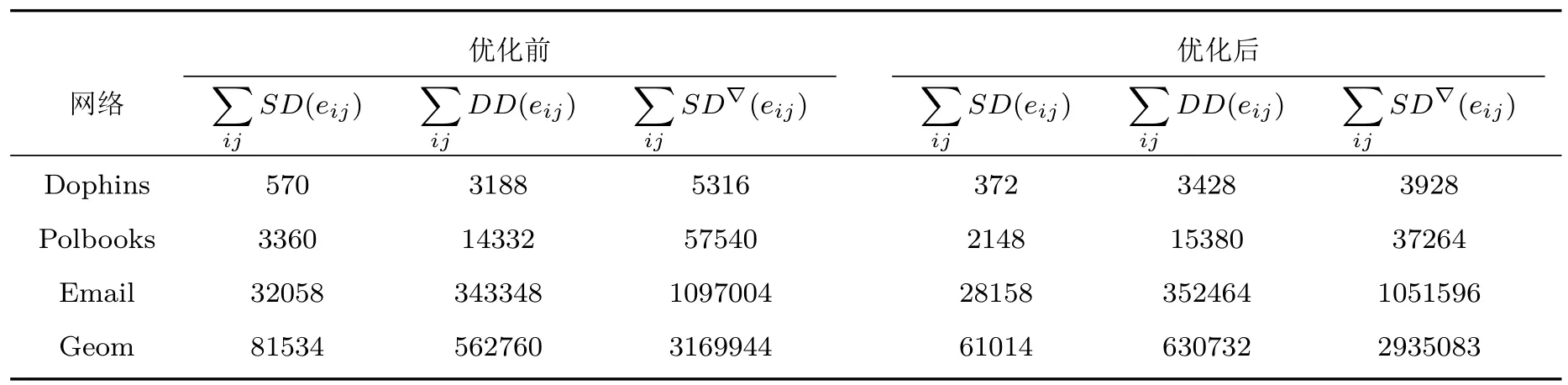
表2 优化前后网络支持度、扩散度与综合特性对比Table 2.Comparison of∑SD,∑DD and∑KSD comprehensive characteristics before and after optimization.

为了观察提出的算法对网络中的所有节点在结构优化前后其信息传播能力的变化,通过在网络结构优化前后分别在网络中利用信息传播模型IC独立级联模型中进行800次蒙特卡罗仿真,记录下将网络中的每个节点作为种子节点进行独立传播的信息覆盖最大范围.定义衡量网络结构变化前后的信息最大覆盖范围的函数Diff(v),

(9)式中,v表示网络的节点,其中v∈[0,N]；COV(v)表示节点v的信息传播的最大范围,即当信息传播结束时,网络中的所有激活节点(接收到信息的节点)占网络中总节点数的比例；COVfi(v)是网络结构优化后的节点v的信息传播的最大覆盖范围.显然,若Diff(v)大于0,则表示以节点v作为信息传播源,在优化后的网络中进行传播相比于优化前的网络,其信息传播范围扩大；否则,传播范围缩小.

图2中,分别在不同的真实网络Dophins,Polbooks,Email和Geom网络中进行信息传播实验,算法待优化的边数m设为网络边数E的10%.对比分析在网络结构优化前后,以网络中每一个节点作为初始传播源观测其传播范围差.从图2中可以看到:在所有的真实网络中,在横坐标线上的节点数量比坐标线下的节点数更多,即表示优化后的网络整体上更有利于增大信息传播的覆盖范围.在Dophins网络中,优化后的网络结构中提高信息传播范围的节点所占的比例为69.4%；Polboks网络中提高信息传播范围的节点所占的比例为79.1%；在Email网络中,提高信息传播范围的节点所占的比例为72.4%；而在Geom网络中,该节点所占的比例为76.7%,即通过算法优化后的网络有利于促进信息传播的节点数总体上不低于网络所有节点的70%.

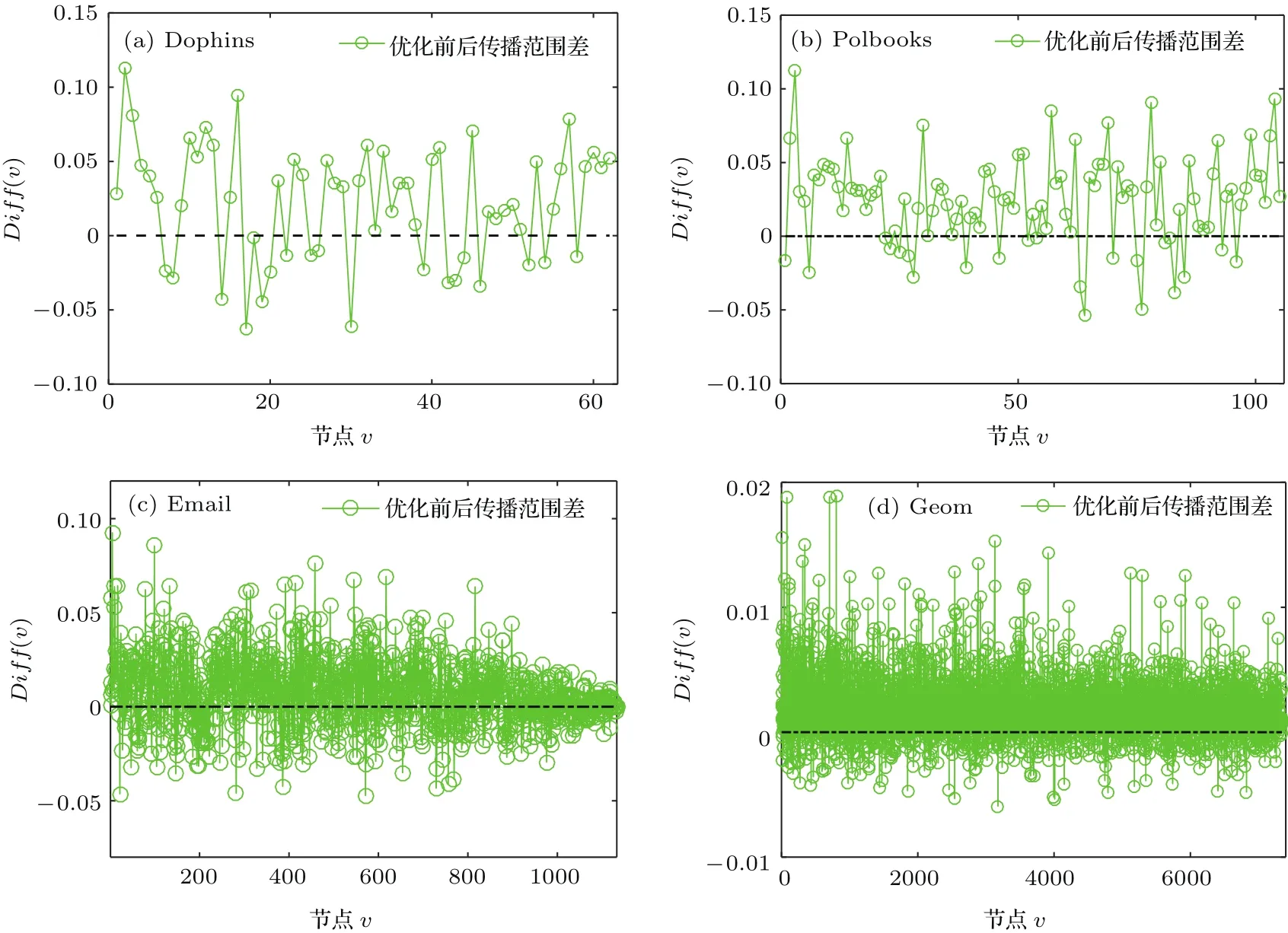
图2 网络优化前后每个节点作为传播源的传播范围差Fig.2.The spread range of each node as a source of propagation before and after network optimization.

为了观察经过算法优化后网络的平均信息传播范围和平均传播速度的变化,对结构优化前后的4个真实网络进行传播能力的仿真实验.实验中,将网络中的每个节点单独作为信息传播源进行传播,记录下节点每个传播时刻t的信息传播情况,并将某一时刻t网络中所有节点传播能力的平均值作为t时刻网络整体对信息的扩散能力.在图3中,通过在4个真实网络中对比分析网络结构优化前后的传播情况可以发现,整体上经过提出的算法优化后的网络对于各个传播时刻t而言,其传播的范围都较为明显地扩大了.信息传播速度刻画的是节点作为传播源进行传播时,网络中被激活节点的变化率,即图3中的曲线斜率.而在4个真实网络中传播到达稳态之前优化网络的时间演化曲线的斜率要高于原始网络,表明优化后的网络信息扩散速度要快于原网络.因此,经过算法优化后的网络对信息的传播能力在传播范围和传播速度上都得到了相应的提高.

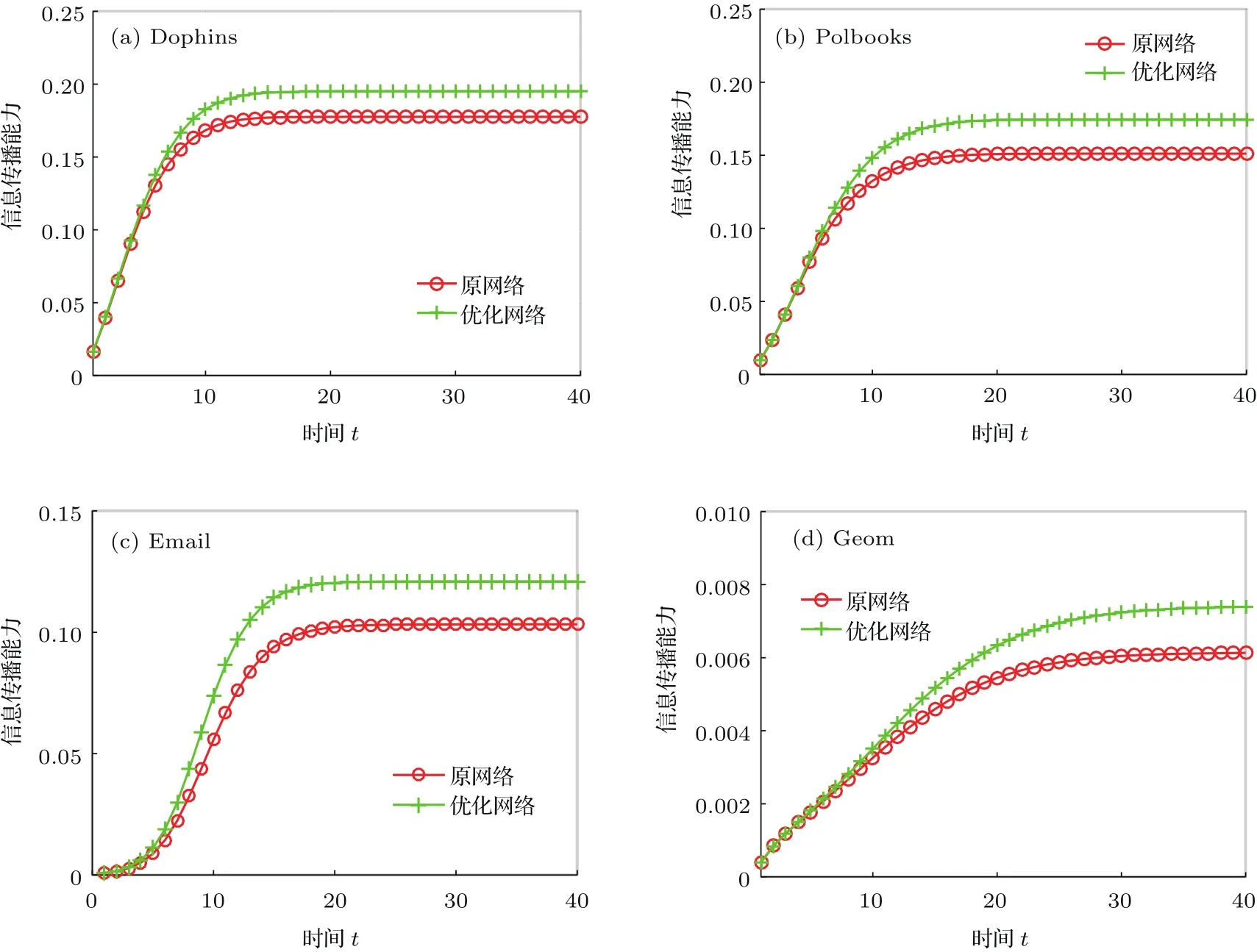
图3 网络优化前后的信息传播时间演化曲线Fig.3.Evolution curve of information propagation time before and after network optimization.

4.3 网络结构优化前后网络统计特性对比分析

为了更明显地观察算法对网络结构的影响,对网络中20%的边进行改写.网络结构在优化前后的变化情况如表3所列,从表3中可见,网络最大度变化不大,网络的最大特征根在Dophins,Polbooks和Geom网络中相应地减小了,而在Email网络中基本保持不变.网络的平均聚类系数、平均路径长度都有下降.从信息传播过程的角度来看,越短的平均路径长度也会使得信息更快速和更高效地传播到网络的其他部分.而提出的算法能够较为明显地改变网络的平均路径长度,即从网络拓扑特征的角度验证了算法对促进信息传播的有效性.

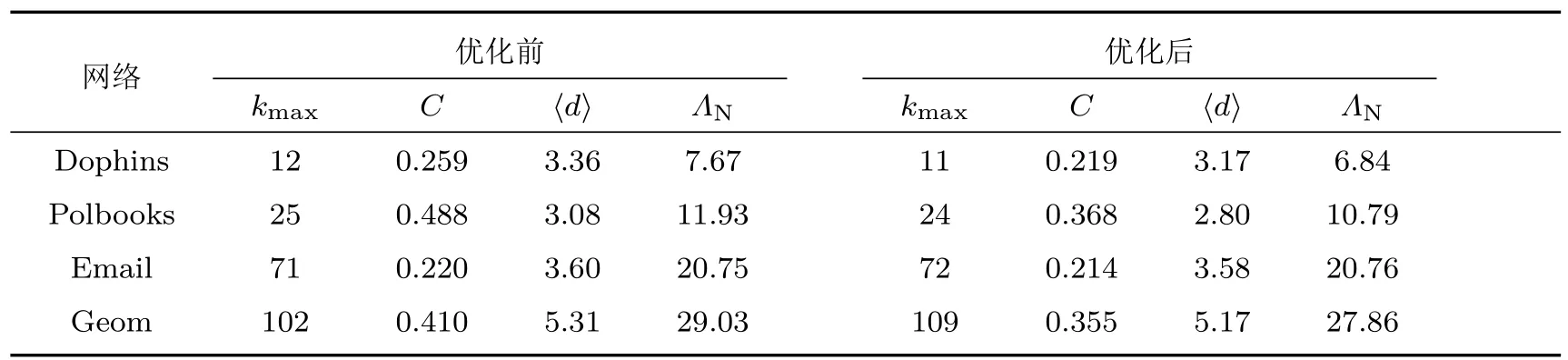
表3 网络优化前后网络统计特征对比Table 3.Comparison of network statistical characteristics before and after network optimization.

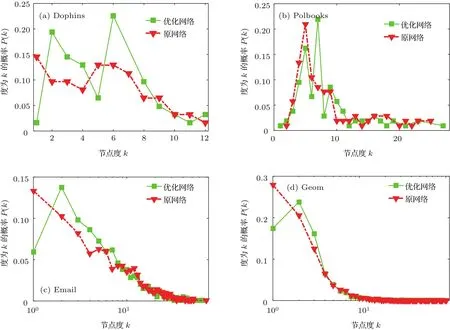
图4 网络优化前后,网络度分布变化比较Fig.4.Comparison of network degree distribution before and after network optimization.

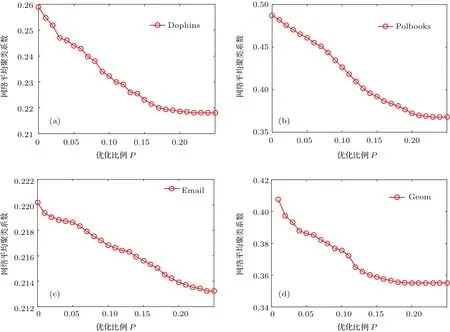
图5 网络聚类系数与改写边比例p的关系Fig.5.The relationship between the network clustering cofiicient and p.

进一步对网络度分布变化进行分析,实验结果如图4所示.在图4中,可以发现在网络的结构优化之后,节点的度分布的特性没有太大变化.从图4(a)、图4(c)和图4(d)可以看出,网络中叶子节点,即k=1的节点比例均有下降.即算法能够较为明显地改变网络中叶子节点数,使得网络中叶子节点减小,网络中其他度的节点数量增加.进一步分析网络聚类特性的变化,从图5可以看出,在进行边改写后,网络聚类系数均下降,在改写边的比例p小于0.2时,聚类系数与p呈反比关系.当 p大于0.2时,聚类系数不再有明显下降.

通过研究算法对网络结构的影响可以发现,经过算法优化后的网络拓扑特征产生了一定的变化,例如平均路径长度、聚类系数和度分布等.然而对于不同网络优化的效果也不同,这与网络本身存在一定关系.因为提出的算法删边的思路是破坏网络中扩散性很低而聚类能力很高的边,在假核(互相紧密连接的局部拓扑结构)中的边大多数是扩散性很低而聚类能力很高的边.因此,当删除这类边时,会瓦解网络中的假核,从而破坏了网络中很多的三角形结构,使得信息能够从假核内有效地传播到网络的其他部分.而对于Email网络,其网络的聚类系数较低,因此算法的整体操作性相对较低,即能够破坏的假核结构较少,对网络结构上的改变不够显著.

4.4 相关参数对信息传播的影响分析

在(4)式中α主要是用来调节边的扩散特性与聚类特性之间重要程度的比例因子,其中α∈(0,1].而在算法中会利用边的扩散特性与聚类特性之间的比例关系来判断是否需要优化一条边.因此,我们研究了比例因子α对信息传播的影响,实验结果如图6所示.在图6中,纵坐标中的稳态时的信息传播能力,是指当信息传播结束时网络中被激活的节点占所有节点的比例.在Dophins网络中,α=0.5时信息传播效果最好；在Polbooks网络中,α在0.4到0.6之间时,传播效果相对更好；对于Email网络,最优的α主要分布在α=0.2和α∈[0.45,0.55]；Geom网络中,最优的α分布在α∈[0.4,0.5]之间.因此,对于不同的网络最优的比例因子有一定的不同,然而最优的比例因子主要集中在0.4到0.6之间.为了使得算法对不同的网络具有普适性,在算法中采用的比例因子α=0.5.

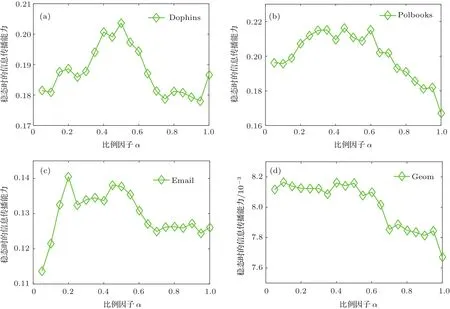
图6 比例因子α对信息传播能力的影响Fig.6.The influence of proportional factor α on information propagation.

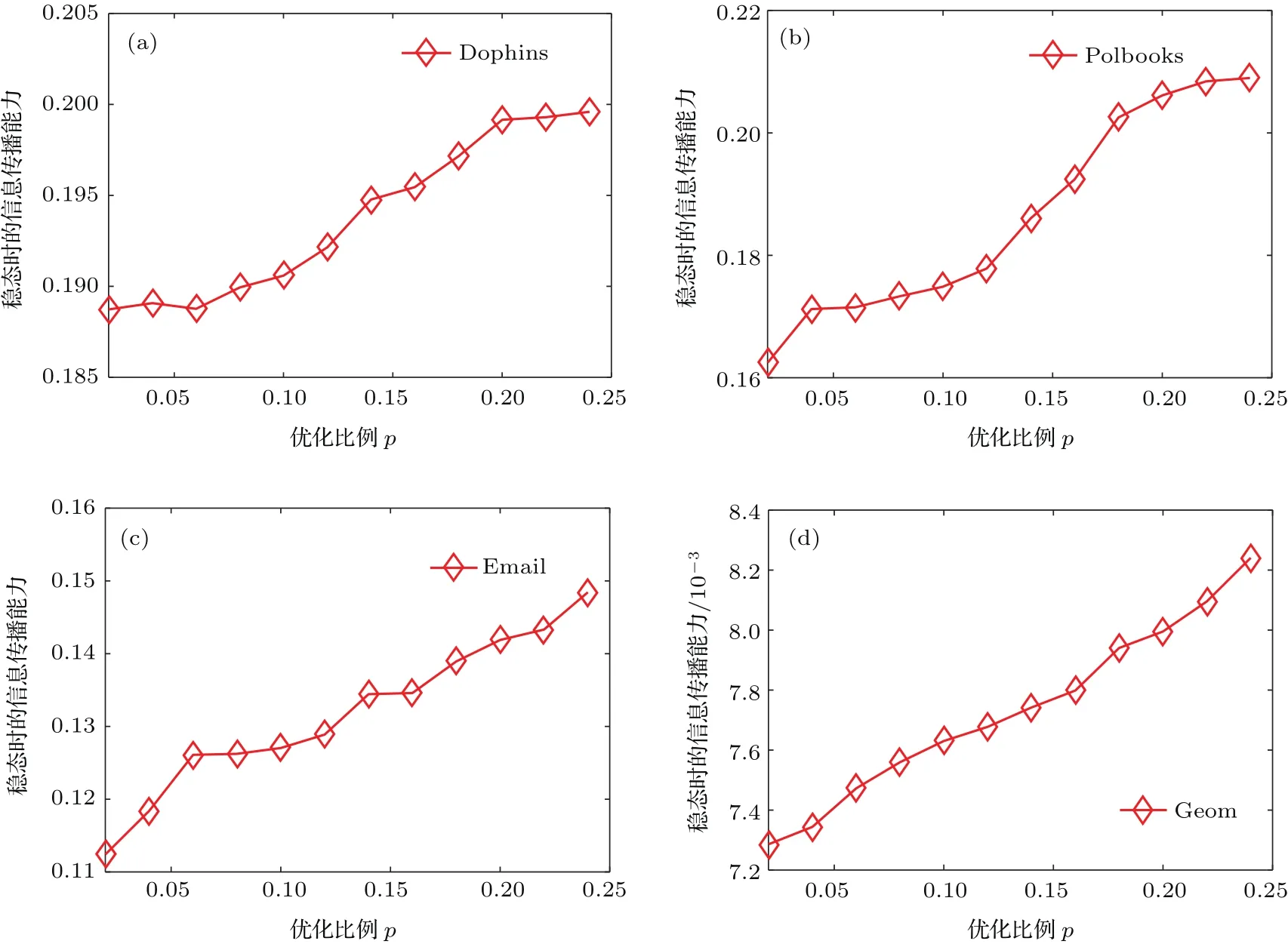
图7 边优化比例p对信息传播的影响Fig.7.The influence of edge optimization proportion p on information propagation.

此外,信息传播的效果与网络中待优化的边数也具有一定的关系.因此,通过优化不同的边的比例 p来观察其对信息传播的影响,实验结果如图7所示.在图7中,横坐标优化比例p的范围为p∈(0,0.25).通过实验结果可以发现,对于不同的真实网络而言,随着优化边比例的提高,即网络中被改写的边结构越多,网络整体对信息的传播能力也在逐渐提高.对于Dophins和Polbooks网络,其网络中的边数较少,能够满足优化条件的边也相应比较少,因此在优化比例p到达0.2时,基本达到实际可优化的边比例,继续提高优化比例后促进信息传播的效果提升并不大.对于Email和Geom网络,随着优化比例p的提高,促进信息传播的效果也越来越好.特别是对于Geom网络,促进信息传播效果与优化比例p之间呈现出接近于线性的比例关系.

5 结 论

本文通过保证节点的总数和边的总数不变的前提下,提出了一种基于扩散K-truss分解的信息传播网络结构优化算法.该算法分析了边的聚类特性与扩散特性之间的相互关系,并根据边的聚类特性与扩散特性之间的差异性来优化网络结构,通过在4个真实的网络中进行信息传播的蒙特卡罗仿真发现,网络中的所有节点中,优化网络结构后提高信息传播范围的节点占所有节点的比例至少为70%,证明了经所提算法优化后的网络使得信息传播覆盖范围更大.网络结构优化后,网络的度分布没有太大变化,但网络的聚类特性下降较为明显,同时网络平均路径长度也有所下降,这些网络特征的变化使得网络中的信息扩散范围扩大.在现实生活中,优化网络结构需要考虑优化网络的成本与带来的效益.而提出的优化算法主要是在需要优化边的局部范围内进行调整,而非全局性调整.这可以大幅的降低优化成本,提高优化效益.因此,可以将优化算法应用在优化成本低、网络拓扑动态可变的网络中,例如自适应Ad hoc移动网络,通过提出的算法进行分析和动态调整网络结构有利于促进节点与节点之间更有效地通信、防止信道过载和提高信息的传输范围.