一种基于随机最优控制的中制导律

徐泽宇，蔡远利

（西安交通大学电子与信息工程学院，西安，710049）

0 引 言

拦截弹是导弹防御系统中的武器部分，拦截弹的制导律设计是导弹防御系统中的关键问题。对于大多数拦截弹，其制导过程都采用初制导+中制导+末制导的复合制导模式[1]。导弹在初制导阶段进行程序转弯，该阶段结束后导弹进入中制导。中制导阶段，利用导弹与目标的相对位置、相对速度等信息形成制导指令使其飞向中末制导交班点。当导引头成功截获目标后，末制导段开始工作。对于先进的导弹防御系统，如萨德及标准-3，中制导是其拦截弹在制导过程中时间最长的1个阶段，因此中制导律的设计显得尤为重要。

中制导律设计的主要目的是将导弹导引到合适的空域内从而能够成功截获目标，并且使导弹在导引头锁定目标时，导弹相对目标的几何关系达到最佳[2]。文献[3]采用预测变结构控制方法进行中制导律的设计，但导弹的速度前置角在中制导过程中变化幅度较大，影响了制导性能；文献[4]提出的一种交班时刻性能最优的中制导律，需要在对预测拦截点进行判断的基础上进行交班点的预测，因此预测精度对制导律的影响较大；文献[5]通过引入伪控制变量设计了一种最优中制导律。但以上工作均没有考虑导弹可能受到随机干扰。因此，为了改善中制导的飞行条件，保证中末制导交班的准确性，应考虑中制导过程中的主要干扰因素，建立合理的弹目运动学模型。

区别于确定性系统的最优控制，随机系统的最优控制[6]不仅考虑被控对象受到的各种随机扰动的影响，而且考虑状态在测量过程中所受到的噪声干扰。为了解决中制导过程中弹目运动模型存在的随机干扰，本文以随机最优控制理论为基础，通过引入一个表示速度前置角积分量的附加状态变量来设计中制导律，并通过仿真验证了该制导律的有效性。

1 导弹与目标运动方程

本文进行以下两点假设：a）导弹在飞行过程中不会发生滚转运动；b）导弹在三维空间的运动可解耦为纵向（俯仰）和侧向（偏航）平面内运动。由于导弹在纵向平面和侧向平面内的运动类似，本文只针对纵向平面的弹目运动来建模并分析制导律。

通常在中制导过程中，目标在导弹视距之外，其机动的几率较小。因此可以通过对拦截点的预测，使导弹导引到目标附近，以较好的交班条件进入末制导。本文所设计的导弹运动模型在中制导过程中瞄准的是运动相对较慢的预测拦截点[7]，两者的相对运动关系及目标的运动如图1所示。

图1 攻击几何平面Fig.1 Engagement Geometry

在纵向（俯仰）平面内，导弹与预测拦截点的相对运动模型[8]为

式中 V为总的随机干扰，假设为零均值高斯白噪声，协方差为G。

纵向平面内导弹运动方程可描述为

纵向平面内目标运动方程可描述为

式中 ξ为导弹运动中的随机干扰，假设为零均值高斯白噪声，协方差为Q；mha ，tha分别为导弹和目标的切向加速度，

2 基于随机最优控制理论的中制导律

2.1 随机最优控制理论

考虑如下随机系统：

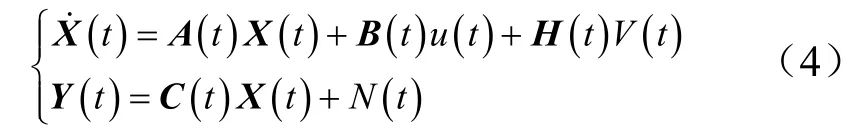
式中 Γ，L和K为加权矩阵。

定义哈密顿泛函：

式中1λ，2λ为待定的伴随函数。

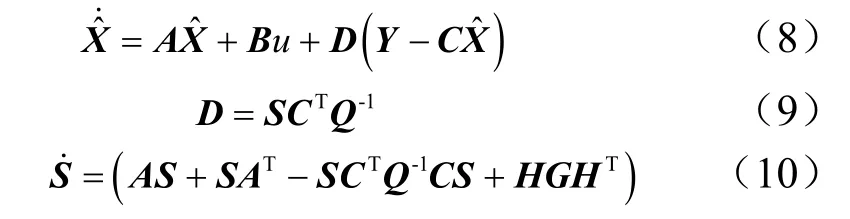
式中 S为观测误差的协方差矩阵。

2.2 随机最优中制导律

通常在中制导过程中，目标机动的几率较小，为实现导弹超视距拦截，可通过对拦截点的预测，使导弹导引到目标附近。在中末交班时，要求导引头指向预测拦截点，使导弹进入末制导后其导引头能够成功捕获目标，从而处于有利的拦截条件。

中远程导弹在中末制导交班点处的角度约束是导引头成功捕获目标的关键。本文所设计的制导律希望在交班点处导引头敏感轴指向预测拦截点，由于中制导段导弹过载较小，因此假设攻角0α≈，这样可以用弹道倾角mθ取代俯仰角ϑ来调整导引头指向，使交班时刻的弹轴指向预测拦截点，即mqθ=。

设导弹的控制量为法向过载，即：

结合式（1）得：

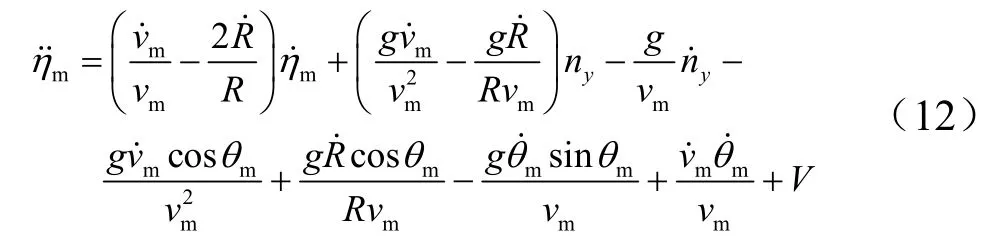
此时，导弹与预测拦截点相对运动的状态空间描述为

观测方程为

考虑控制能量和交班时刻的角度约束，选取如下性能指标函数：

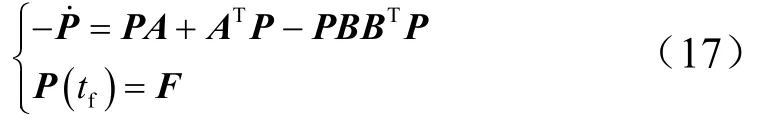
在中末制导交班的时刻，为了使导弹弹轴对准预测拦截点，需要使速度前置角[9]为0，取1f→∞，f2=0，于是，

2.3 带有积分量的随机最优中制导律

本节在随机最优控制理论的基础上，推导了一种新的中制导律，主要思想是构建一个附加状态变量，即速度前置角的积分量。所设计的制导律仍然希望在交班点时刻导引头敏感轴指向预测拦截点，即mqθ=，使速度前置角满足约束条件。

导弹的控制量仍为法向过载yn，表达式与式（11）一样，mη˙˙与式（12）相同。

此时，导弹与预测拦截点相对运动的状态空间描述如式（14）所示。但

对应的观测方程为

考虑控制能量和交班时刻的角度约束，性能指标形式上如式（16）所示。但其中半正定对称矩阵对应的最优控制且满足式（17）的Riccati方程。

中末制导交班时刻的条件与2.2节相同，这里只需要使速度前置角的积分量为0，因此取1f→∞，20f= ，30f= ，求解得：

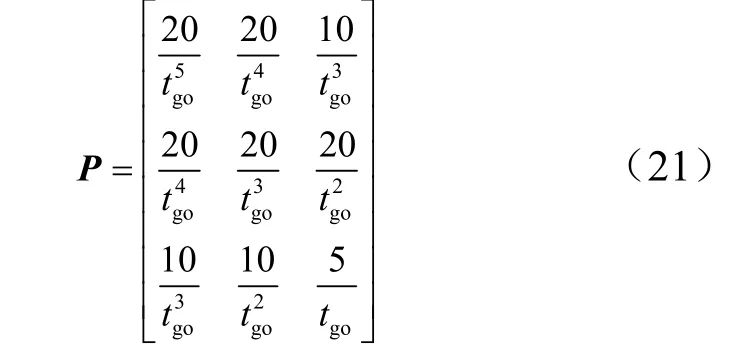
3 仿真结果及分析

假设目标做简单机动飞行，初始时刻目标位置为（50 km，10 km），速度tv=800 m/s，切向加速度法向加速度目标的初始弹道倾角为180°；导弹中制导初始时刻的位置（2 km，1 km），速度mv=900 m/s，切向加速度初始时刻弹道倾角为24°；雷达导引头的锁定距离为11 km（中末交班距离）。

在无干扰的标称情况下，将本文第 2节所提出的两种中制导律与比例导引进行仿真比较，比较结果如图2所示。由图2可知，带有积分量的中制导律对应的弹道较为平滑，更能有效地指向预测拦截点。

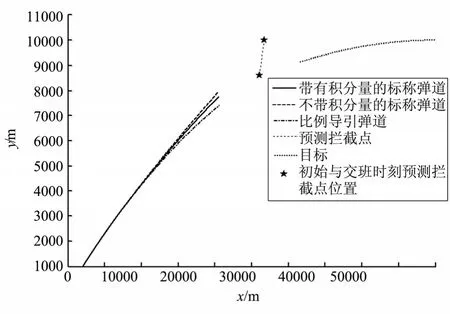
图2 中制导轨迹曲线Fig.2 Midcourse Guidance Trajectory

图3为导弹速度前置角速率变化曲线。由图3可知，本文所设计的两种制导律在中末交班时刻都能使速度前置角变化率很小。

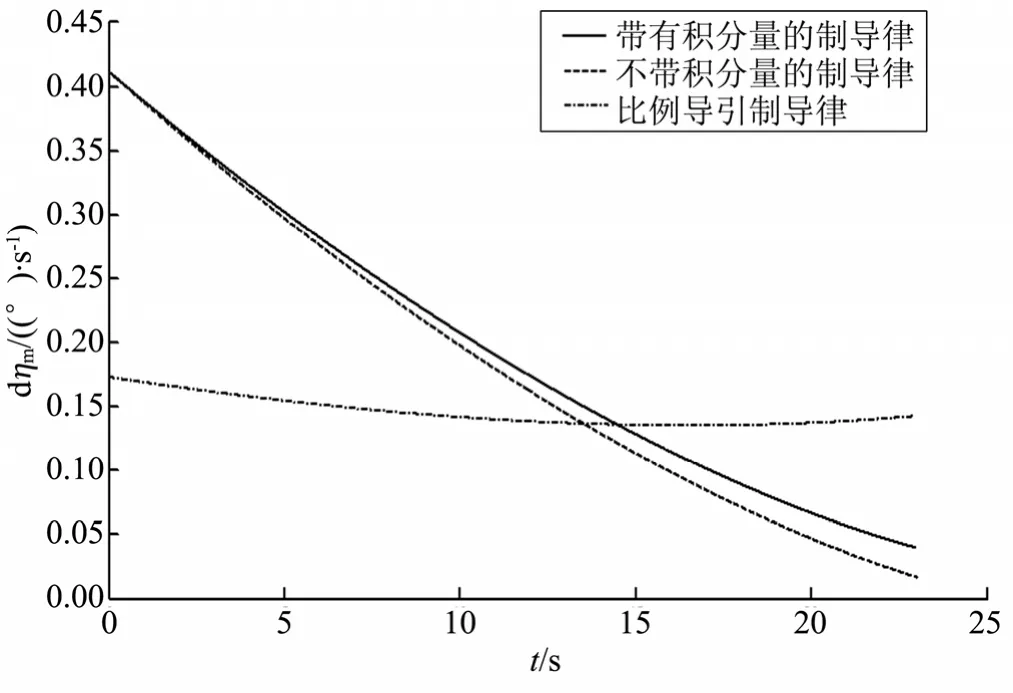
图3 导弹速度前置角速率变化曲线Fig.3 Curve of Missile Velocity Deflection Angle Rate

图4为导弹过载曲线。由图4可知，相比于比例导引，带有积分量的中制导律会使导弹法向过载有所增加，但总体仍然不大，较为合理，图 5为导弹速度前置角变化曲线。由图5可知，带有积分量的中制导律在中末交班时刻能够使速度前置角几乎为0，可以认为导引头指向预测拦截点，保证目标进入导弹视距时，导弹处于易于捕获目标的几何位置。

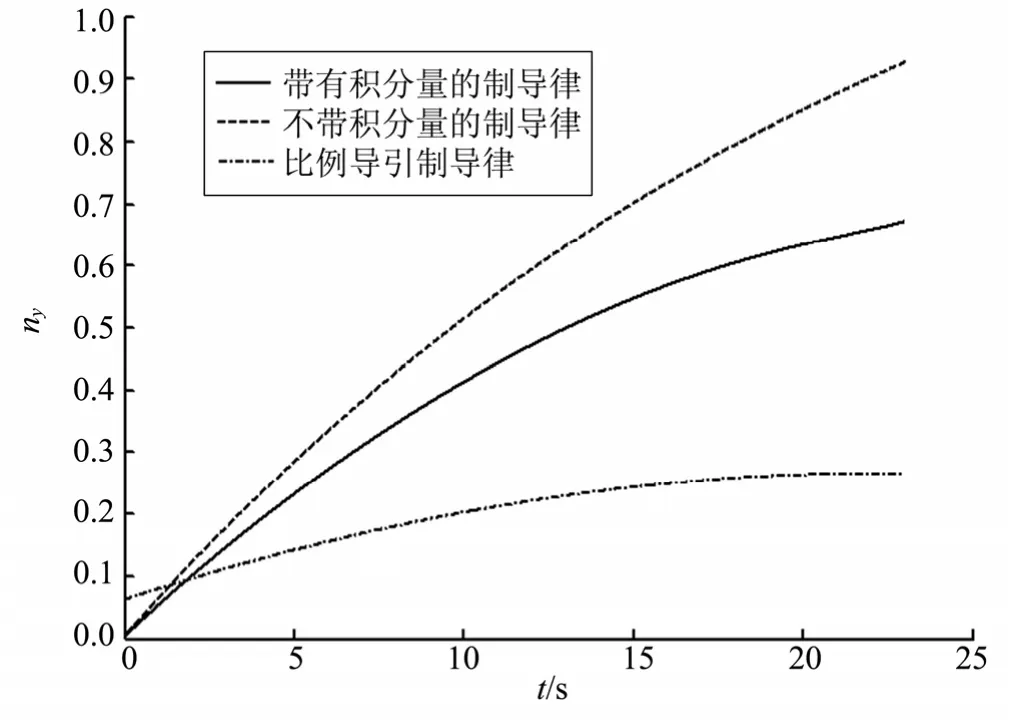
图4 导弹过载曲线Fig.4 Missile Overload Curve

图5 导弹速度前置角变化曲线Fig.5 Missile Velocity Deflection Angle Curve

在随机干扰的情况下，对带有积分状态变量的中制导律进行仿真，并与标称情况进行比较，比较结果见图 6～9。由图 6可知，较标称情况下的弹道，存在干扰的弹道同样平滑并且与标称弹道轨迹几乎一致；由图7可知，导弹过载比标称时大，但总体仍很小；由图8和图9可知，本文所设计带有积分状态变量的中制导律在存在过程干扰和观测干扰的情况下，仍能在一定范围内保证导引头指向预测拦截点。仿真结果表明，本文所设计的中制导律也具有较强的鲁棒性。

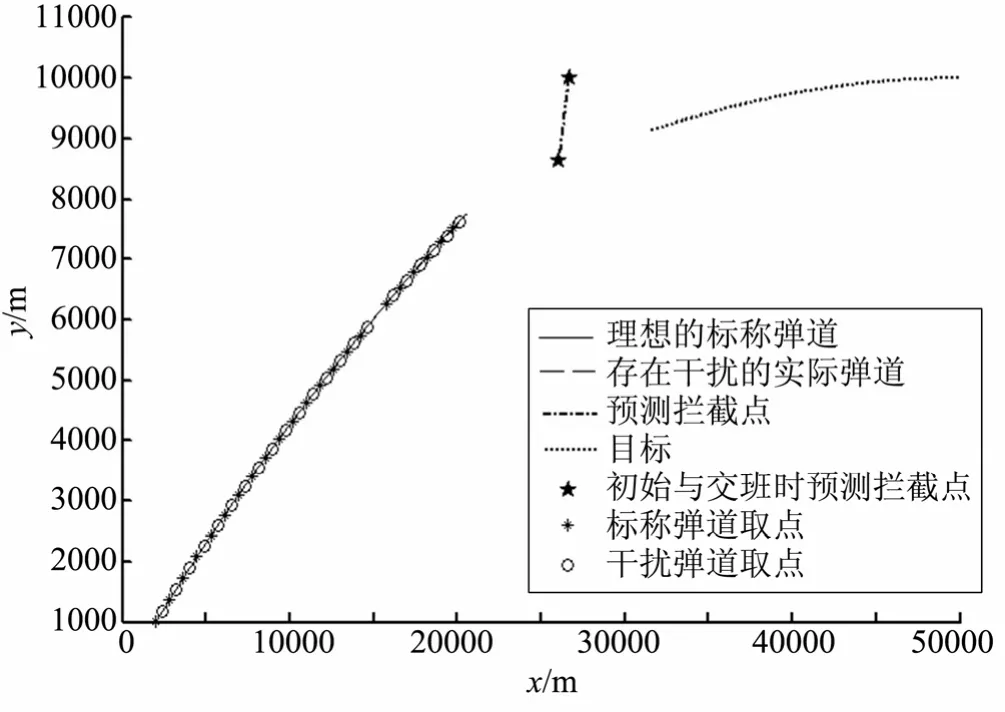
图6 考虑随机干扰时的中制导轨迹曲线Fig.6 Midcourse Guidance Trajectory with Stochastic Disturbance

图7 考虑随机干扰时导弹过载曲线Fig.7 Missile Overload Curve

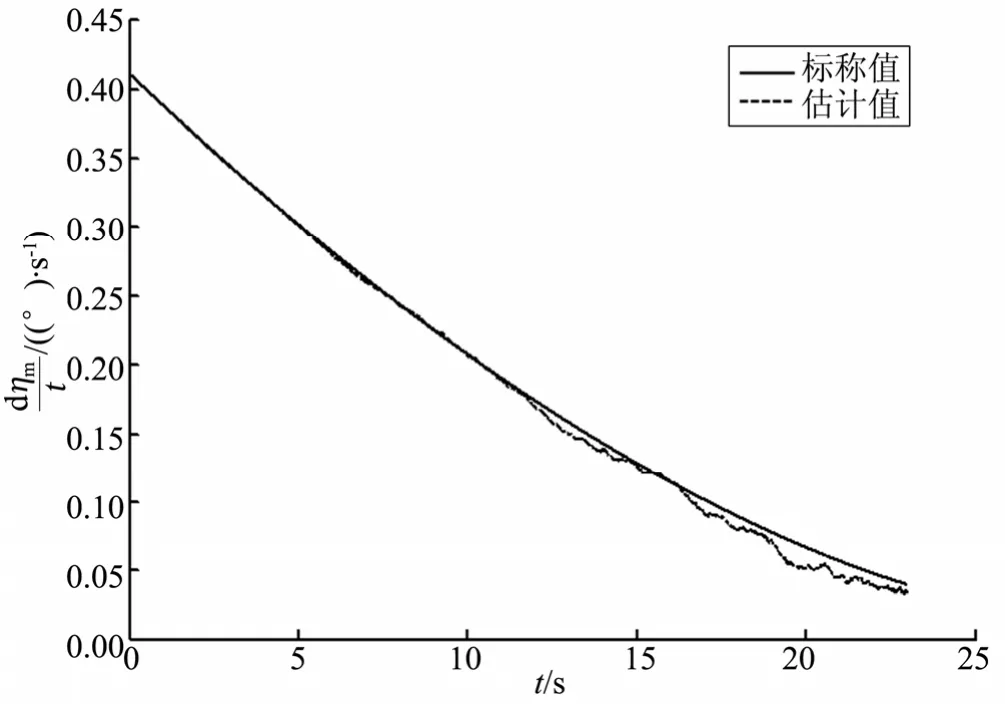
图8 考虑随机干扰时导弹速度前置角速率变化曲线Fig.8 Curve of Missile Velocity Deflection Angle Rate

图9 考虑随机干扰时导弹速度前置角变化曲线Fig.9 Missile Velocity Deflection Angle Curve

4 结 论

本文以随机最优控制理论为基础，在中制导过程中建立存在随机干扰的弹目运动模型，并通过构建一个表示速度前置角积分量的附加状态变量，得到一种新的中制导律。仿真结果表明：该制导律能够有效地完成中末制导的交班，确保导弹在末制导开始时拥有良好的攻击条件，从而提高导弹在末制导段的拦截能力和最终的制导精度。后续工作中，将对目标不同的机动形式以及在三维空间进行中制导律的研究。