基于遗传算法的单螺杆钻具型线优化设计

孙兴伟，郭钦元，孟栋轩，韩 煜，杨赫然

(1.沈阳工业大学 机械工程学院，辽宁 沈阳 110870； 2.长庆油田分公司 机械制造总厂，陕西 西安 710201)

0 引言

对于螺杆马达的型线，要求啮合副曲线凹凸处过渡光滑，若存在打结点，将会造成定、转子间的泄漏或干涉[1-2]。

在处理螺杆钻具廓形光顺性的问题上，常用的方法是光顺能量法，该方法是在适当的约束条件下修改控制点，使其应变能最小，它是一种全局优化方法[3]。该方法十分繁琐，而且可能改变无需调整的型值点。针对这一问题，本文提出一种基于遗传算法的以控制顶点坐标值的变化量作为优化变量的局部光顺算法，光顺后可直接得到新的型值点，有较强的实用性。

1 B样条曲线拟合算法的实现

1.1 螺杆马达啮合原理及啮合副设计要求

假设做平面行星运动的5头螺杆钻具如图1所示。在运动过程中，定转子的啮合条件是转子与定子头数以及导程比为N∶N+1，并且啮合线连续[4]。实际工程中，型线精度应严格遵循设计要求，避免啮合过程中的噪声，减少螺杆马达的传动损失[5]。

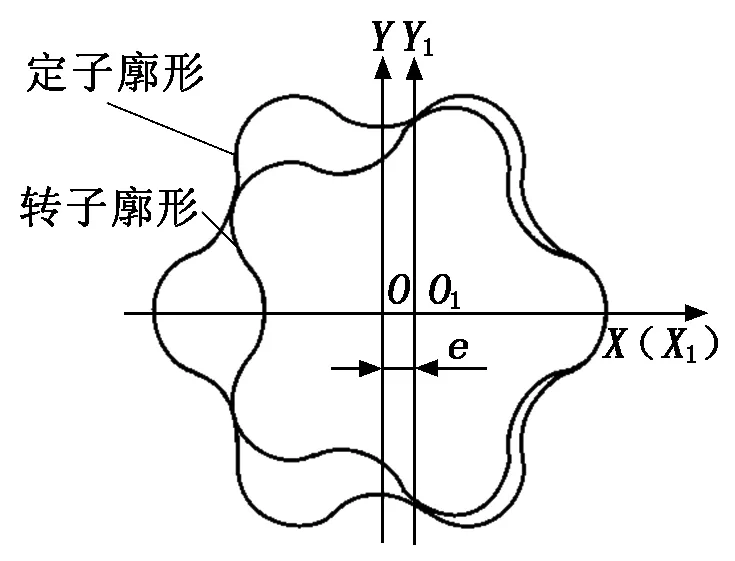
图1 螺杆钻具啮合图

1.2 B样条曲线拟合理论

通过实验测得一组螺杆钻具廓形数据点Mi，t次B样条曲线表达式如下[6]:

(1)

其中：Bi,t(u)为定义在节点矢量u上的基函数。

1.3 曲率求解和尖点检测

为了找出螺杆钻具廓形的不光滑点，将拟合后的样条曲线表达式作两次降阶处理，分别得到t-1次及t-2次B样条曲线。通过B样条曲线的参数方程可得曲率表达式，将经过降次的样条曲线的坐标值代入曲率表达式中可得到螺杆钻具廓形曲线的曲率。

通常情况下，如果拟合曲线满足曲率为局部最大值点或大于某一给定阀值，则认为拟合曲线不光滑，即存在尖点。

2 螺杆钻具型线的局部光顺算法

本文采用遗传算法对单螺杆钻具型线进行光顺处理。分析中将包括螺杆钻具型线尖点在内的相邻五点的变动量xj作为染色体，染色体长度为l。

2.1 适应度函数

螺杆钻具型线设计的重要指标之一是最大综合曲率最小，为达到这一目的，应尽量加强廓形曲线的光顺性，因此，本文将曲线能量和曲率变化作为遗传算法的适应度函数，构造优化模型如下：

(2)

适应度函数反映个体优劣性，适应度函数越小说明个体越优，螺杆钻具廓形曲线能量较小且曲率变化均匀。

2.2 遗传操作

为实现选出优良染色体的目标，比较变动后的型值点与原型值点的个体适应度值，并按照降序排列，选出与种群数相同数量的最优个体进行下一步的遗传操作[7]。采用线性交叉和高斯变异法对父代染色体进行遗传操作，形成新一代种群。

3 仿真实验结果和分析

3.1 实验结果

测量螺杆钻具截面上的点，得出一组定子外径为172 mm的5头转子半个周期的99个数据，用B样条曲线拟合得到的截面半周期廓形曲线如图2所示。根据1.3节中的的曲率求解算法进行尖点检测，结果如图3所示，在横坐标为41.592 mm处曲线曲率为局部最大值，导致型线不光顺。

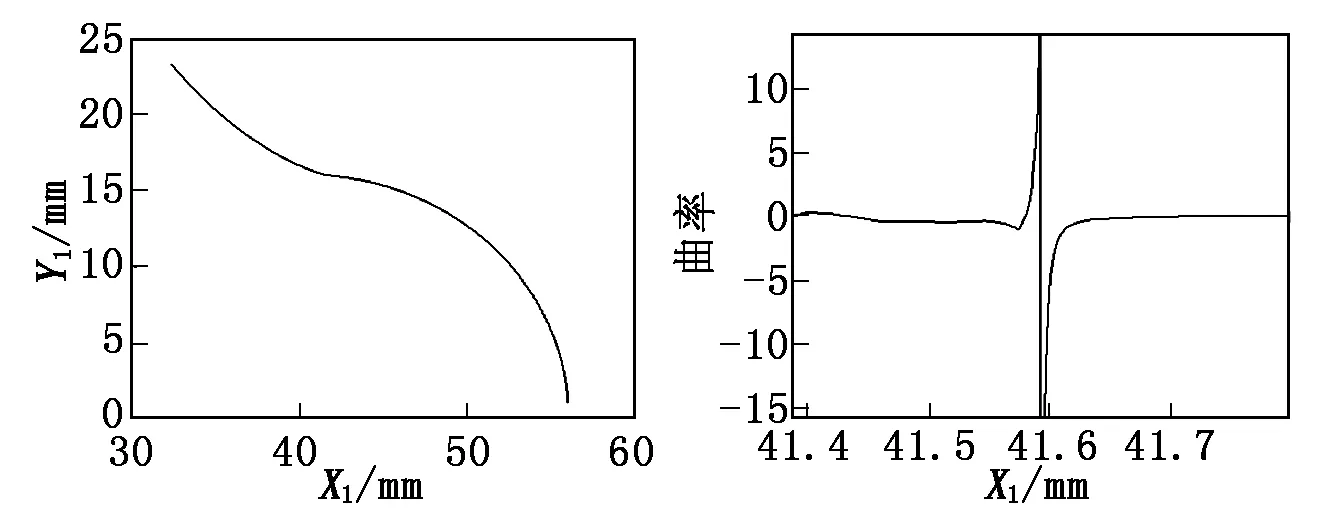
图2截面的半周期廓形曲线图3拟合曲线曲率

遗传算法中，变异操作与交叉操作是进化中生成新种群的重要手段，如果概率太小，会丢失种群的多样性；概率太大，容易破坏有利模。因此变异概率一般取0.1～0.4，此时算法的鲁棒性和收敛性最好，本文取变异概率pm=0.2；交叉概率一般取0.4～0.9，本文取交叉概率pc=0.7。确定种群规模为30，光顺容差ε=0.08，利用遗传算法对螺杆钻具型线进行优化，图4为光顺前后的廓形，图5为优化后的型线曲率。

图4 优化前后廊形对比

螺杆钻具型线的凹凸曲线过渡处存在曲率变化，由图5可看出，优化后的螺杆钻具型线曲率在-2～2之间，根据适应度函数计算此时的曲线能量。优化前后螺杆钻具廓形曲线的坐标点及能量变化如表1所示。

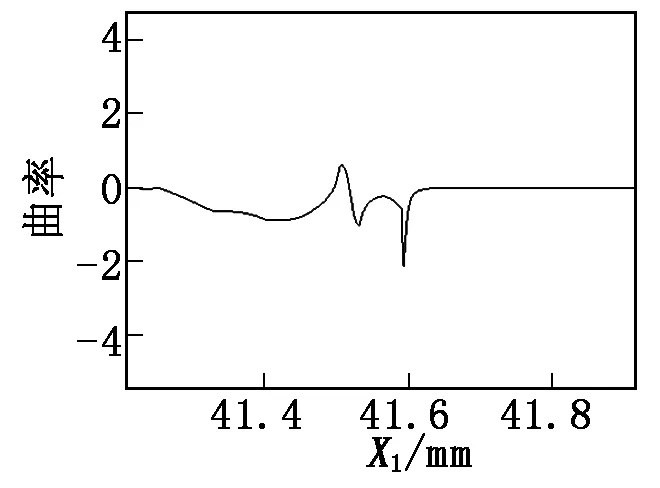
图5 优化后型线曲率

从表1中可以看出：光顺后螺杆钻具型线的能量小于光顺前的型线能量，说明优化后的曲线光顺性较好。

表1 优化前后螺杆钻具廓形曲线型值点及能量变化

3.2 螺杆钻具啮合性能分析

如图6和图7所示，在未优化之前，螺杆钻具啮合点个数是1 826，优化后的啮合点个数为1 872，较优化前明显增多，说明本文所使用的算法可以提高螺杆钻具的密封性，改善螺杆渗油情况，增加钻具使用寿命。

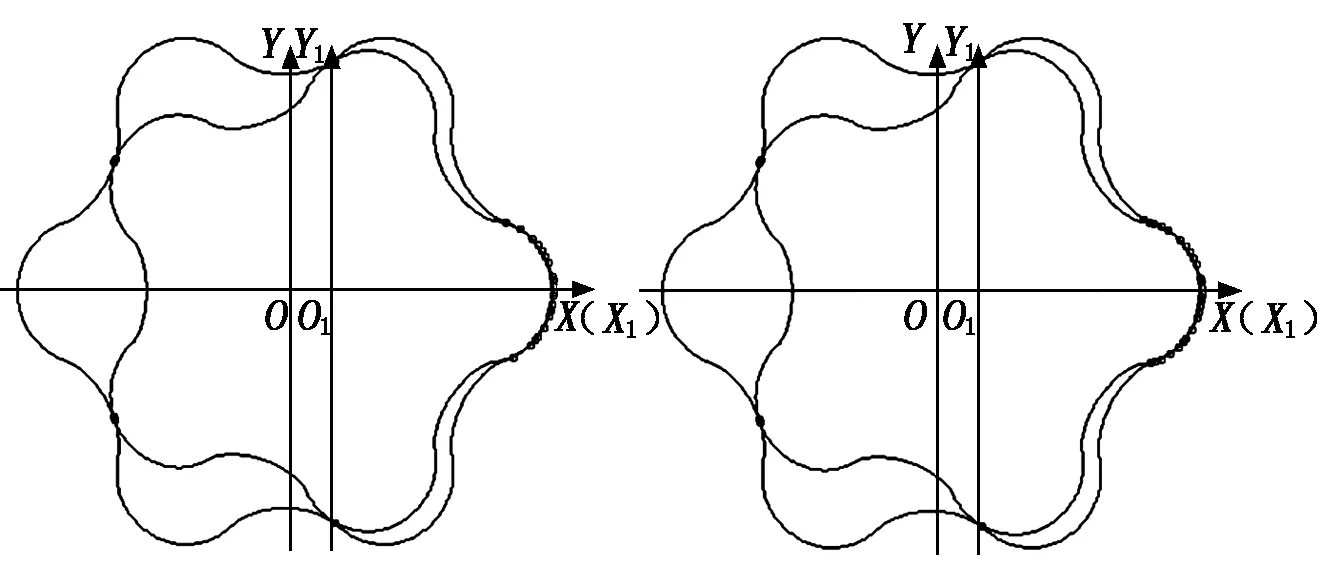
图6优化前啮合情况图7优化后啮合情况

4 结语

本文以型值点坐标值的变化量作为优化变量，运用能量及曲率最小原理，结合遗传算法直接得到光顺的型值点。通过对实例的研究分析可知，优化后的螺杆钻具廓形曲线能量减小，啮合点数增加，说明本文提出的遗传算法能够有效解决廓形曲线不光滑的问题，是一种准确有效的算法。