RV减速器动力学特性研究

赵海鸣，聂 帅，朱加云，蔡进雄

(1.中南大学 机电工程学院，湖南 长沙 410083； 2.中南大学 高性能复杂制造国家重点实验室，湖南 长沙 410083； 3.湖北三江航天万峰科技发展有限公司，湖北 孝感 432000)

0 引言

RV(Rotate Vector)减速器是20世纪80年代由日本最先研发并投入使用的减速传动装置，具有传动比大、刚度强、回差小等优势，在工业自动化以及航空航天等科技领域得到广泛应用[1-4]。RV减速器主要应用在机器人大臂或底座等高负载关节，该工况下对RV减速器的刚度及精度要求很高，因此研究RV减速器的动力学特性十分必要。本文拟对RV减速器整机的动力学特性进行研究，并完成关键零部件的模态分析，为RV减速器结构的优化及综合性能的提升奠定基础。

1 RV减速器动力学模型的建立

RV减速器原理图如图1所示，它是两级封闭差动轮系减速传动装置，第一级传动为渐开线齿轮传动，第二级传动为摆线针轮传动[5]。

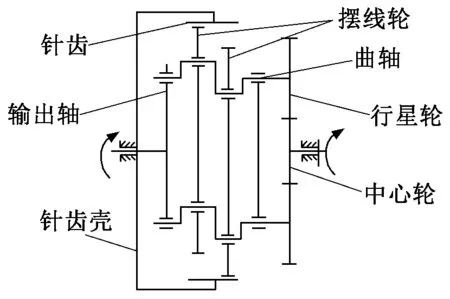
图1 RV减速器结构原理图

本文以RV160-E为例建立其动力学模型。在第一级减速机构中，将行星轮与中心轮啮合部分等效为弹簧连接模型，而剩下的部分则等效为集中质量。在第一、二级减速机构间，通过花键分别将行星轮与相应的曲柄轴一端部连接，将二者等效为一体；将曲柄轴与行星轮啮合部分等效为弹簧连接；而剩下的部分则等效为集中质量。在第二级减速机构中，将摆线轮与针齿啮合部分等效为弹簧连接，而剩下的部分则等效为集中质量。RV减速器动力学模型如图2所示。

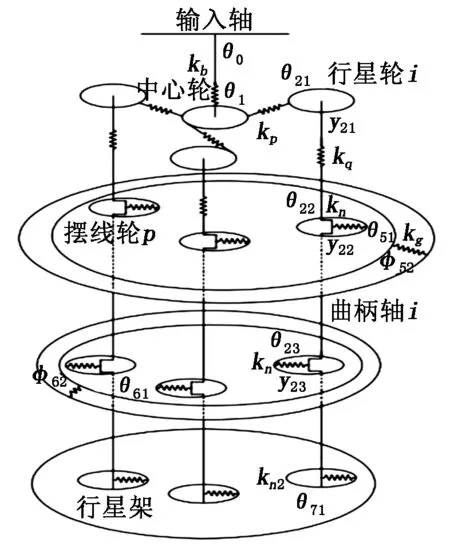
图2 RV减速器动力学模型

图2中，渐开线齿轮的啮合刚度为kp，摆线针轮的啮合刚度为kg，输入轴的扭转刚度为kb，曲柄轴的扭转刚度为kq，偏心轴承的刚度为kn，支撑轴承的刚度为kn2；中心轮的基圆半径为rb，行星轮的基圆半径为rp，曲柄轴分布圆半径为rh，摆线轮节圆半径为rc；偏心距为a；θ21、θ22、θ23、y21、y22、y23分别为曲柄轴2在行星轮、两偏心处的扭转角和线位移，J21、J22、J23、m21、m22、m23分别为曲柄轴2在行星轮、两偏心处的转动惯量和质量，其余曲柄轴同理；θ51、φ52分别为摆线轮1自转与公转的扭转角，J51、J52分别为摆线轮1自转与公转的转动惯量，摆线轮2同理；θ71、J71分别为行星架的扭转角和转动惯量。

1.1 渐开线齿轮传动轮系动力学模型的建立

输入轴传递转矩过程中，设k0为输入轴扭转刚度，J0为输入轴的转动惯量，θ0为输入轴振动扭转角度，θ1为主动渐开线齿轮的振动扭转角度，则输入轴的振动方程为：

(1)

其中：Tin为RV减速器的输入转矩。

设α1为渐开线齿轮啮合角，k1、J1分别为主动渐开线齿轮的啮合刚度和转动惯量，则其振动方程为：

J1θ1=k0(θ0-θ1)+k0(θ21rp+y21cosα1-θ1rb)rb+k1(θ31rp+
y31cosα1-θ1rb)rb+k1(θ41rp+y41cosα1-θ1rb)rb.

(2)

1.2 曲柄轴动力学模型的建立

设曲柄轴受到偏心轴承在切向方向的支持力分别为FAt与FDt，曲柄轴端部受到的行星轮啮合力为F[6]，曲柄轴受力情况如图3所示。

设曲柄轴结构的广义坐标为：

{θ21，θ22，θ23，θ31，θ32，θ33，θ41，θ42，θ43，y21，y22，y23，
y31，y32，y33，y41，y42，y43}.

相对应的质量矩阵为：

{J21，J22，J23，J31，J32，J33，J41，J42，J43，m21，m22，
m23，m31，m32，m33，m41，m42，m43}.

故曲柄轴2的动力学方程为：

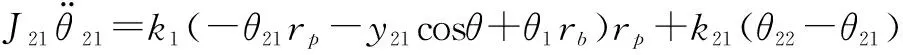
(3)

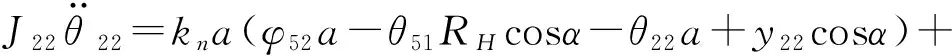
(4)

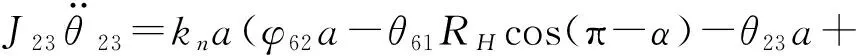
(5)

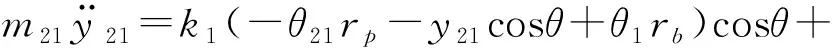
(6)

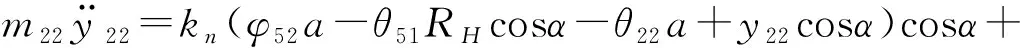
(7)

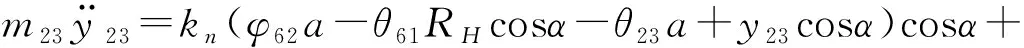
(8)

其中：α为曲柄轴扭转角；RH为偏心轴承分布圆半径；k21、k22为曲柄轴的扭转刚度。

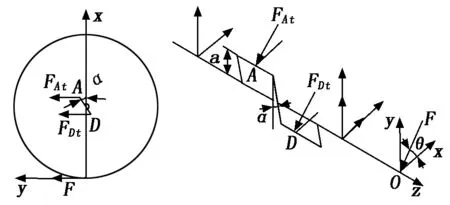
图3 曲柄轴受力分析图情况

1.3 摆线轮动力学模型的建立

取摆线轮的广义坐标为{θ51，θ61,φ52,φ62}，相对应的质量矩阵为{J51,J61,J52,J62},则摆线轮1的动力学方程为：

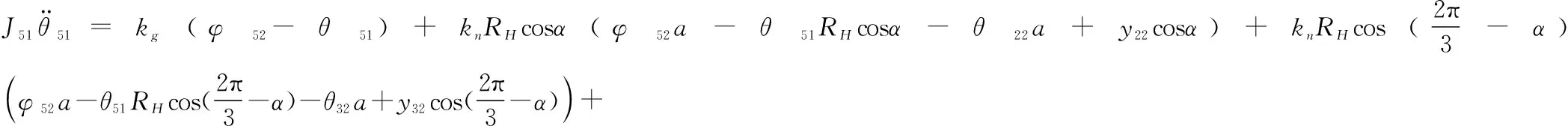
(9)

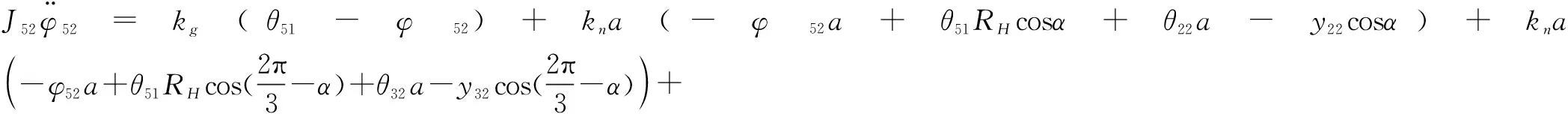
(10)

1.4 行星架动力学模型的建立

行星架在曲柄轴公转运动的作用下进行自转运动。设支撑轴承分布圆半径为RL，行星架的动力学方程为：

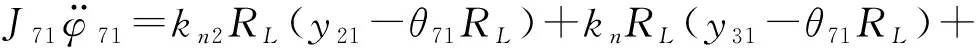
(11)

2 RV减速器动力学模型的求解

系统动力学模型的求解即固有频率的求解是动力学分析汇总的基本内容[7]。系统动力学方程可描述为：

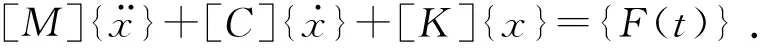
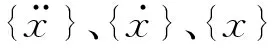
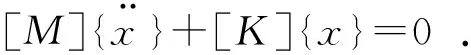
对应的特征方程为：

([K]-ω2[M]){x}=0.

其中:ω为系统的固有频率。

计算ω只需在MATLAB上调用函数:[V,D]=eig(K,M)。

本文建立的系统刚度矩阵如下：

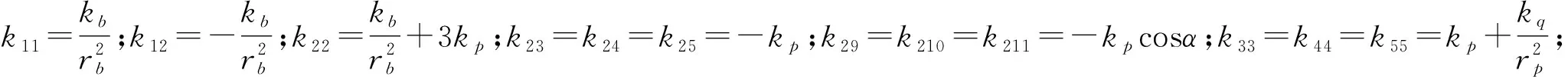
其中的β为曲柄轴两个偏转轴线平面和曲柄轴、摆线轮中心轴线平面的夹角。

系统质量矩阵如下：

2.1 轴类扭转刚度计算

圆柱轴扭转刚度的表达式为：

(12)

其中:G为弹性剪切模量；Ip为极惯性矩；l为轴长。

阶梯轴扭转刚度计算公式如下：

(13)

其中:ki为第i段轴的扭转刚度。

输入轴为齿轮阶梯轴，可忽略轴端齿轮的影响，将其等效为阶梯轴，结构尺寸如图4所示。

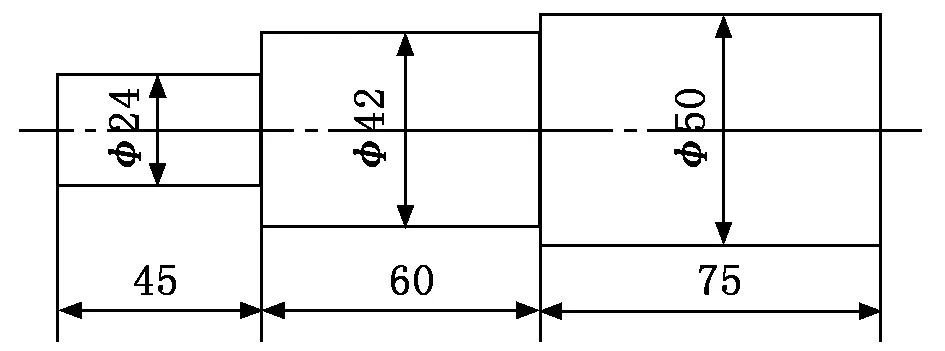
图4 输入轴结构尺寸

曲柄轴可直接按照圆轴扭转刚度公式计算，此处轴径为Φ20 mm、长度为65 mm。

将相关数据代入式(12)和式(13)可得输入轴的扭转刚度和曲柄轴的扭转刚度分别为47 054 N·m/rad、19 333 N·m/rad。

2.2 轴承刚度计算

滚动轴承刚度计算公式为[8]：

(14)

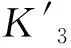
RV减速器的轴承主要有偏心轴承及支撑轴承，基本参数如表1所示。

表1 轴承基本参数

将相关数据代入式(14)可得偏心轴承刚度和支撑轴承刚度分别为1.02×109N/m、8.175×108N/m。

2.3 渐开线齿轮啮合刚度计算

齿轮啮合刚度的表达式如下[9]：

cr=(0.75εα+0.25)c′.

(15)

其中:εα为齿轮端面重合度，εα=1.568；c′为单对齿啮合刚度，c′=1.29×108N/m。

由式(15)计算可得渐开线齿轮的啮合刚度为1.846×108N/m。

2.4 摆线针轮啮合刚度计算

摆线针轮接触模型如图5所示，摆线针轮整体啮合刚度不是各个单齿啮合刚度单纯叠加[10]。

图5 摆线针轮接触模型

实际应用中摆线轮与针齿同时啮合齿数将少于总齿数的一半[11]，因此在叠加计算摆线针轮整体等效扭转刚度时加入调整系数λ(一般取λ为0.6～0.7)。摆线针轮整体等效扭转刚度表达式为：

(16)

其中:zb为摆线轮齿数;Ki为第i个针齿与摆线轮接触的刚度；li为第i个针齿啮合点的公法线至摆线轮中心的距离。

由式(16)计算可得摆线轮等效扭转刚度为5.159×105N·m/rad。

2.5 RV减速器固有频率计算

通过本文建立的刚度、质量矩阵，利用MATLAB得到的RV减速器前10阶固有频率如表2所示。

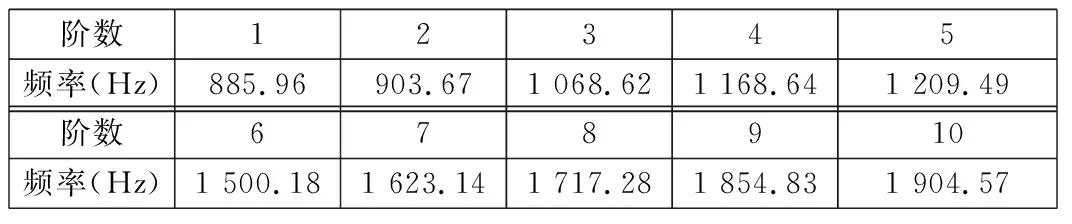
表2 RV减速器前10阶固有频率

系统固有频率只取决于系统的刚度与质量，从总体上看，不论单自由度系统还是多自由度系统，都遵循系统质量增大、刚度减小降低系统固有频率这一规律，因而研究关键零部件的动态特性不仅可以反馈整机的动态特性，还可以优化整机结构。

3 RV减速器关键零部件有限元模态分析

本文对RV减速器关键零部件进行模态分析，计算出关键零部件摆线轮、曲柄轴和行星轮的固有频率及相应振型，以避免共振和有害振型的出现。RV减速器各关键零部件材料参数如表3所示。

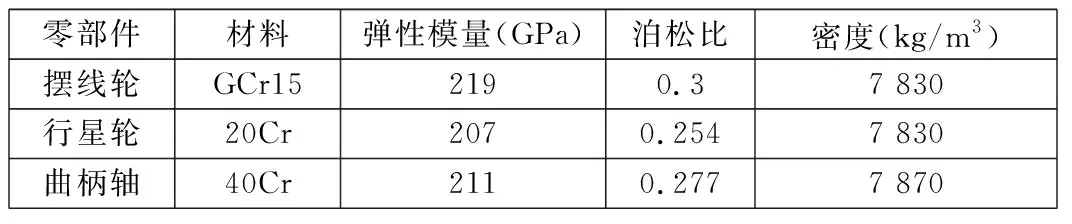
表3 各关键零部件材料参数

3.1 摆线轮的模态分析

边界条件设置：在摆线轮中心孔添加圆柱面约束，约束径向及轴向位移，保证其绕中心孔轴线的旋转自由度。进行模态分析求解出摆线轮的前10阶固有频率，如表4所示。

由表2和表4可知，系统的第2、第3、第5阶固有频率与摆线轮的第3、第4、第5阶固有频率比较接近，可适当提高摆线轮的刚度来避开共振区域。

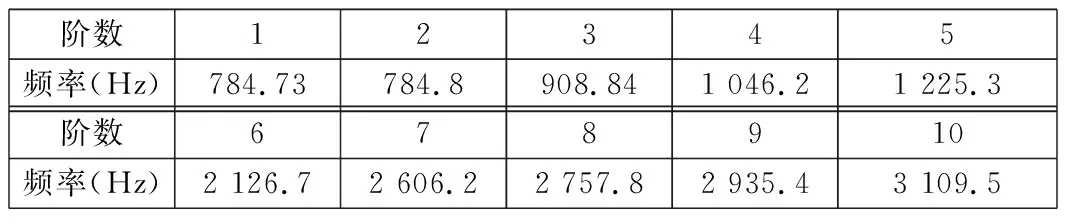
表4 摆线轮前10阶固有频率

3.2 曲柄轴的模态分析

边界条件设置：在4个圆轴段表面添加圆柱面约束，约束轴向及径向位移，保证偏心和同心部分的旋转自由度。进行模态分析求解出曲柄轴的前10阶固有频率，如表5所示。

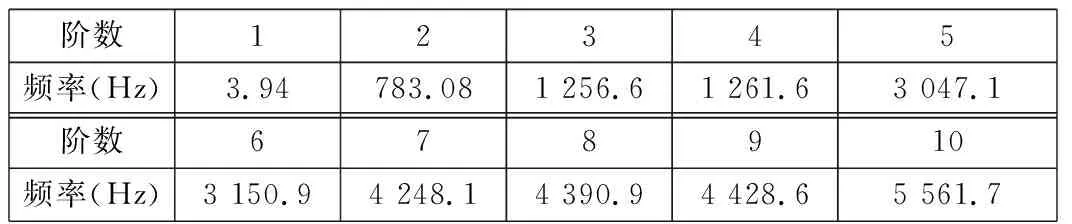
表5 曲柄轴前10阶固有频率

曲柄轴的第3、第4阶固有频率与系统的第5阶固有频率比较接近。同样地，可适当改变行星轮的质量和曲柄轴的刚度来避开共振区域。观察振型图(见图6)可知，最大位移集中发生在行星轮与曲柄轴啮合处，这对啮合处的刚度有了一定要求并且为曲柄轴的优化设计提供了参考依据。

图6 曲柄轴第2阶、第6阶振型

4 结论

综合考虑RV减速器工作过程中的各影响因素，建立了十六自由度的RV减速器整机动力学模型，根据牛顿定律和广义坐标法建立了关键零部件的动力学方程。利用MATLAB计算出系统的固有频率及相应振型。利用ANSYS Workbench对主要零部件进行了模态分析，得到了它们的固有频率和振型，分析表明摆线轮的固有频率不在整机的固有频率点上。观察振型图显示应提高曲柄轴啮合处的刚度，为曲柄轴的优化设计提供了参考依据。