基于多重分形理论的地铁车辆平轮故障诊断
王锋涛,敖银辉
(广东工业大学 机电工程学院,广东 广州 510006)
0 引言
车轮是轨道车辆的关键部件,踏面故障会造成轮轨间剧烈的振动冲击,在不同车速、轮重及损伤程度下,其冲击载荷甚至能达到正常情况的数十倍。异常冲击不仅会形成环境噪声,影响乘车舒适度,而且会严重破坏钢轨和路基[1]。
多重分形理论能够很好地反映振动信号的集合结构特征,并能全面描述振动信号的波动程度和振动的剧烈程度,为机械设备故障诊断提供了一种有效的方法。张淑清[2]等对滚动轴承的振动信号进行多重分形特征提取,并用模糊C均值聚类进行分类,取得了良好的故障识别效果。李冬冬[3]等用多重分形谱和支持向量机的检测方法,实现了行星齿轮箱的故障检测。张美兰[4]等用多重分形与异谱分析理论,实现了高速列车运行状态有效识别。褚青青[5]等计算振动时间序列的多重分形谱能和广义分形维数谱能,并用神经网络算法进行识别,实现了齿轮箱故障的准确判别。
支持向量机对于小样本、非线性数据的识别,具有许多特别的优势[6]。邢宗义[7]等用粒子群优化的支持向量机对城轨列车的轮对尺寸进行了预测,证实了其可行性和有效性。陈芳[8]等用遗传算法优化的支持向量机实现了对齿轮箱故障的识别,并与神经网络算法进行对比,结果表明支持向量机在故障识别方面有更好的表现。本文基于多重分形理论对地铁车辆平轮故障进行诊断。
1 多重分形理论
多重分形理论最早由Mandelbrot提出,能更好地描述振动信号的局部特征。其算法如下[9]:
1.1 测度的定义
将振动信号在时间域内分割为N个尺度为δ的小方格,Si(δ)是尺度为δ时第i个小方格内信号的幅值之和,则可以将概率测度Pi(δ)表示为:
(1)
1.2 配分函数的定义
将Pi(δ)用q次方进行加权求和,得到配分函数Χq(δ):
(2)
其中:q为权重因子,q>1时,Pi(δ)大的值对Χq(δ)起主要作用,q<1时,Pi(δ)小的值对Χq(δ)起主要作用。
1.3 质量指数的定义
Χq(δ)在无标度区间内和质量指数τ(q)有以下的计算关系:
Χq(δ)=δτ(q).
(3)
则质量指数为:
(4)
1.4 奇异指数的定义
质量指数的一阶导数为奇异指数a(q):
(5)
1.5 多重分形谱的定义
对质量指数进行勒让得变换,可以得到振动信号的多重分形谱f(a):
f(a)=q·a(q)-τ(q).
(6)
2 构建多重分形特征
2.1 多重分形谱的最大值fmax
多重分形谱的最大值fmax能表示振动信号大、小峰值的变化速度,因此可以反映故障振动信号的局部奇异性[10]。
2.2 多重分形谱的宽度Δa
多重分形谱的宽度Δa为:
Δa=amax-amin.
(7)
Δa越大,概率测度分布越不均匀,信号的多重分形性越强,即信号的波动程度越剧烈;反之,信号的多重分形性越弱,信号越稳定,变化越平缓。
2.3 最大、最小概率多重分形谱的差Δf
最大、最小概率多重分形谱的差Δf为:
4.创新开展全员法制教育。法律的意义不仅仅在于运用法律手段解决已经出现的法律纠纷,更重要的在于对可能出现的风险运用法律手段进行防控。所以,结合油田企业的实际,创新开展全员法制教育,提高全员守法经营、依法维权的法律意识,对于法律风险防控制度体系的有效性将产生深远的影响。
Δf=f(amin) -f(amax).
(8)
Δf>0说明信号的变化剧烈,奇异性比较强;Δf<0表明信号光滑,变化平缓。
2.4 最小奇异指数amin
amin越小,反映信号变化快速,正则性比较弱,信号的波动程度越大;反之信号越平滑。
根据多重分形理论和多重分形谱,可以确定以下5个特征向量amin、Δa、f(amin)、Δf(a)、fmax,用来表示信号的变化趋势和多重分形特征,并通过支持向量机来实现故障的分类与识别。
3 基于多重分形理论的地铁车辆平轮故障诊断方法
基于多重分形理论的地铁车辆平轮故障诊断方法具体步骤如下:
(1) 分别采集地铁车辆轮对4种工况下的轮轨振动信号。
(2) 利用小波包分解降噪方法对轮轨振动信号进行降噪预处理。
(3) 计算振动信号的多重分形谱参数作为故障特征:[amin,Δa,f(amin),Δf(a),fmax]。
(4) 用遗传算法优化支持向量的两个参数:核函数参数g以及惩罚因子c。
(5) 建立支持向量机分类器,将故障特征值作为分类器的输入,对轮对的故障进行识别。
4 实验过程与数据处理
4.1 实验环境
为了能更好地提取到轮轨振动信号,在广州地铁1号线芳村站轨道内侧安装8个振动加速度传感器L1~L8,同时利用3个车轮传感器W1~W3作为系统控制信号,W1控制信号启动系统,W2控制起始采样信号,W3控制终止采样信号。L1~L8的现场安装如图1所示,传感器布置简图如图2所示。

图1 传感器现场安装示意图
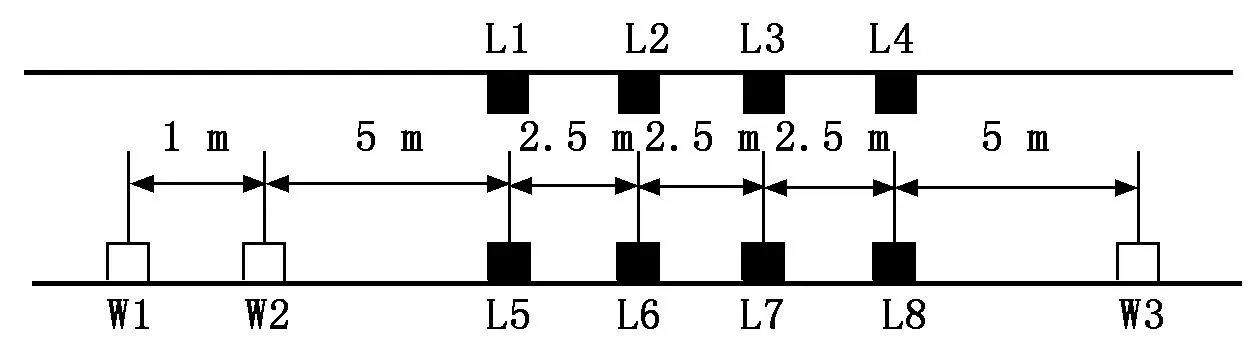
图2 传感器布置简图
为了有效提取振动信号的特征,对原始振动信号进行小波包去噪处理。图3为采集到的4种不同工况下原始振动信号的时域图,图4为采集到的4种不同工况下原始振动信号小波包去噪后的时域图。

图3 4种工况下原始振动信号时域图

图4 4种工况下振动信号小波包降噪时域图
4.2 利用多重分形谱提取信号特征
利用小波包去噪后的数据计算4种工况下振动信号的多重分形谱,如图5所示,并对4种工况的多重分形谱作特征提取,结果如表1所示。从图5中可以看出,信号的多重分形谱曲线都是上凸函数,这表明了轮轨振动信号具有多重分形特性,而且不同工况下振动信号的多重分形谱有明显的区别,因此可以用多重分形谱的参数作为故障特征进行工况类型的分类和识别。
Δα反映信号在分形基础上的概率度量的不均匀程度,Δf表示振动信号中最大、最小振幅的变化速度,两者都反映了振动信号的波动性程度。分析表1可知:相比踏面正常工况,其他3种故障工况下,Δα和Δf都有不同程度增加,踏面剥离时其值最大,这是因为踏面剥离造成的轮轨冲击较强,振动信号波动变化较大,其多重分形特征相较其他工况更加明显,其次是踏面擦伤和圆周磨耗状态。
4.3 车辆平轮故障识别
建立精确的支持向量机识别模型,需要确定模型核参数g和惩罚因子c两个变量。本文采用遗传算法优化支持向量,得到两个参数的最优结果为:g=1.722 4,c=0.632 6。
对4种工况分别取50组样本,输入到支持向量机中进行训练得到分类模型,再针对每种工况分别另取10个样本输入训练模型中,作为测试集进行故障识别,其分类效果如图6所示。由图6可以看出,只有2个测试集样本分类错误,整体的识别准确率为95%,取得了较好的分类效果。为了验证本文所提方法的有效性,利用没有经过小波包去噪的原始振动信号提取多重分形特征进行故障识别,分类准确率只有75%,分类效果如图7所示。
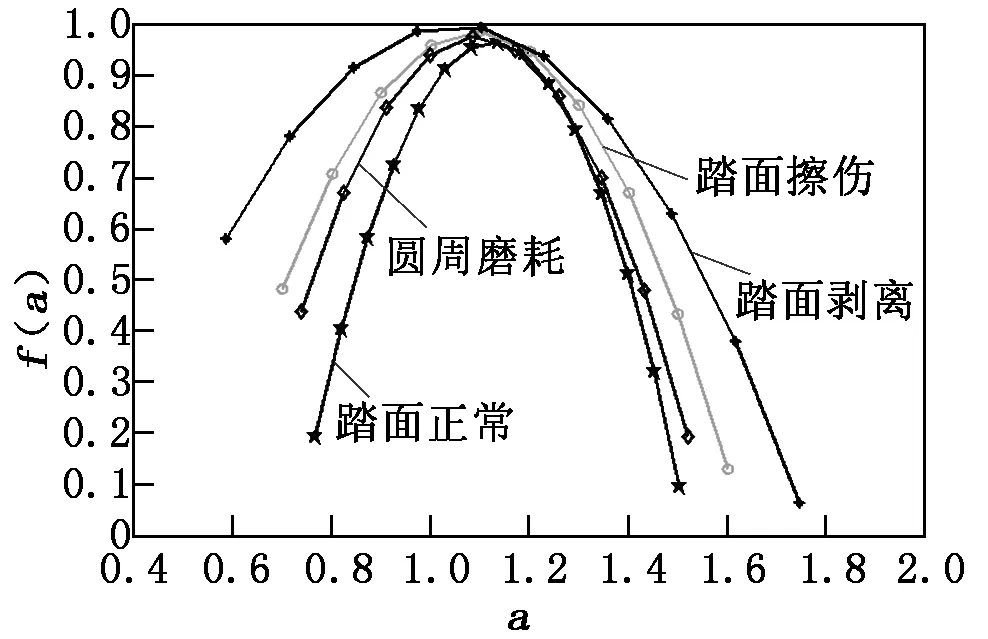
图5 4种工况下振动信号的多重分形谱
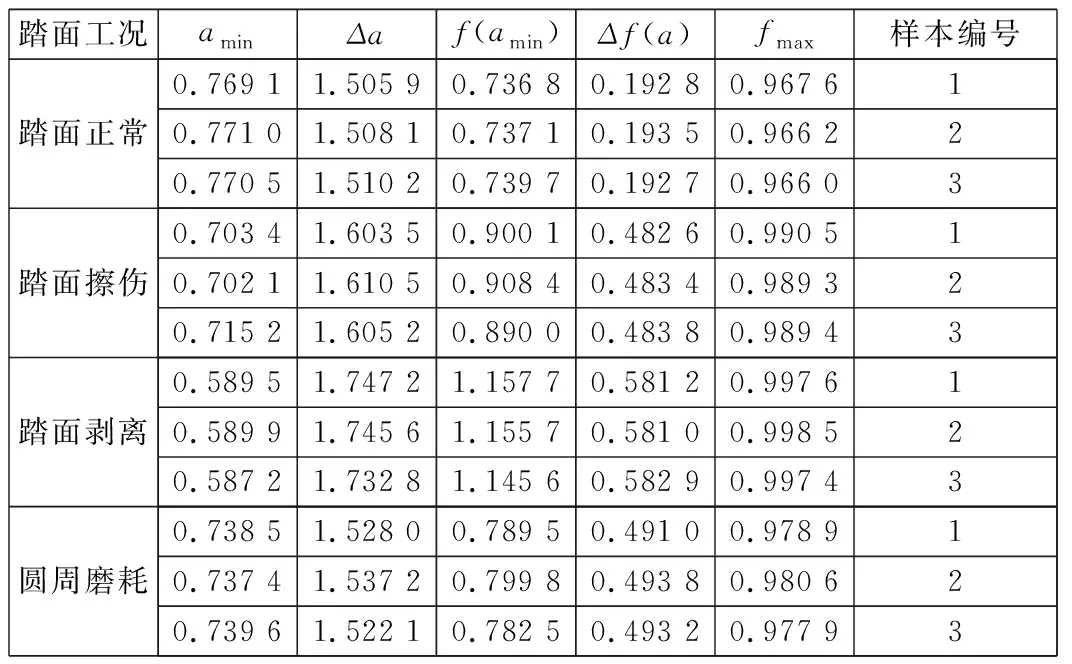
踏面工况aminΔaf(amin)Δf(a)fmax样本编号踏面正常0.769 11.505 90.736 80.192 80.967 610.771 01.508 10.737 10.193 50.966 220.770 51.510 20.739 70.192 70.966 03踏面擦伤0.703 41.603 50.900 10.482 60.990 510.702 11.610 50.908 40.483 40.989 320.715 21.605 20.890 00.483 80.989 43踏面剥离0.589 51.747 21.157 70.581 20.997 610.589 91.745 61.155 70.581 00.998 520.587 21.732 81.145 60.582 90.997 43圆周磨耗0.738 51.528 00.789 50.491 00.978 910.737 41.537 20.799 80.493 80.980 620.739 61.522 10.782 50.493 20.977 93
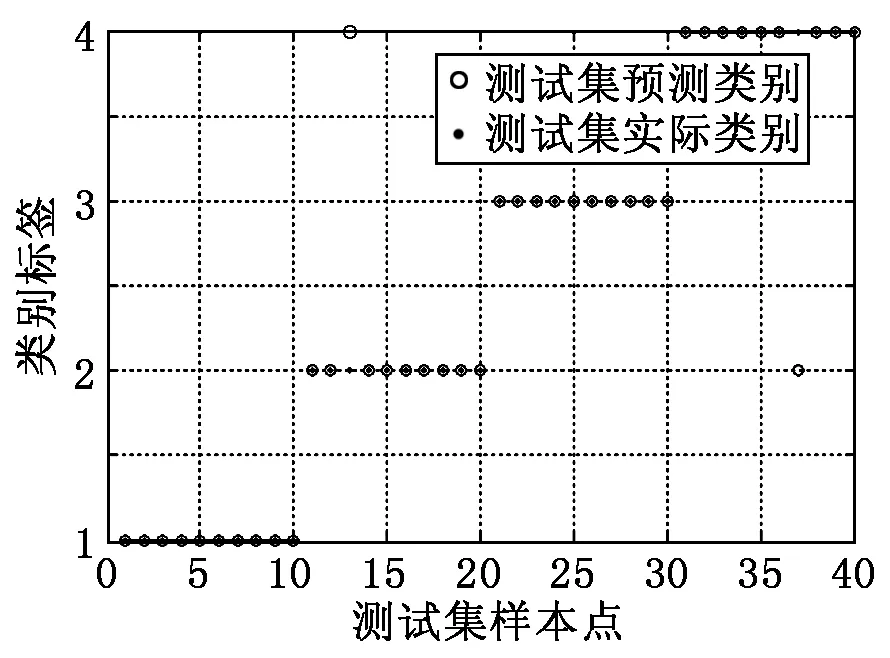
图6 去噪信号测试集分类效果
5 结语
针对地铁车辆轨道振动信号非平稳性、信噪比低等特点,利用多重分形理论对车辆平轮振动信号进行分析,结果表明4种不同工况下振动信号的多重分形谱有着明显的不同, 因此可作为故障特征量来识别地铁车辆轮对的不同工况。
本文采用的故障识别模型识别准确率可达97.5%,实现了车辆平轮故障的准确判别,为车辆平轮的故障诊断提供了一种新思路。实验发现,基于多重分形理论的信号分析方法对信号的噪声比较敏感,如何能更好地去除和减弱噪声的影响,需做进一步的研究。
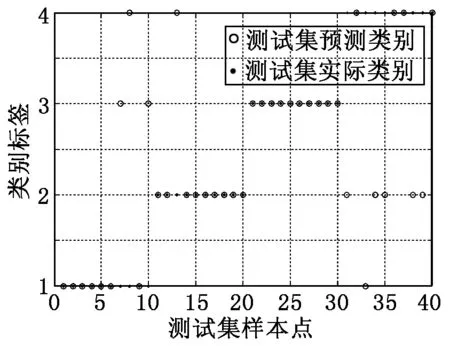
图7 原始信号测试集分类效果

