基于模仿学习的人机协作的研究

陈龙新，曾 翔，吴鸿敏，廖亚军，银江涛

(1.广东工业大学 机电工程学院，广东 广州 510006； 2.广东岭南职业技术学院 数控教研室,广东 广州 510663)

0 引言

机器人应用领域的不断扩张和对机器人智能化要求的不断提高，促使人机协作成为机器人领域的热门话题与研究方向。人机协作可以让机器人更好地与人配合，提高生产效率，更好地适应当前大规模“个性定制”的生产需求。从20世纪90年代开始人们对协作机器人的本体设计进行了十分深入的研究，然而针对协作型机器人开发的协作系统的研究却鲜有成熟的商业产品，这不利于协作型机器人的应用与推广。近年来，有越来越多的学者投入到人机协作的研究中来[1]，人机协作水平将成为衡量机器人优劣的重要指标。

模仿学习是指模仿者通过“观察”示教的运动行为，学习运动控制策略，进而获取运动技能[2]。基于模仿学习的人机协作，通过简单地示范机器人如何协作人完成任务，同时记录人和机器人的状态数据用于对交互概率模型进行训练，从而描述任务过程中状态的时空差异性。本文提出了一种基于模仿学习的方法来实现人机协作任务,并以协作型机器人Baxter作为实验平台，结合交互概率模型搭建人机协作系统，通过实验验证模型的可行性。

1 人机协作机器人系统

本文搭建人机协作机器人系统开展研究，其主要硬件如图1所示。以协作型机器人Baxter作为实验平台开展研究，该机器人在零力拖动模式下可拖动机器人末端到任意的可达空间进行任务的示范。同时，我们需要记录人机协作任务示范过程中人的状态[3-6]。本文中，我们采用体感相机Xtion，通过ROS(Robot Operating System)的程序包openni_tracker实现对人体骨架的跟踪，以此针对人机协作任务对人和机器人的运动进行建模。

图1 人机协作机器人系统的主要硬件设备

仅通过人的运动状态来推测任务是有明显缺陷的。假设以下情形：人手持不同物体执行着不同的任务，而运动轨迹却十分相似。在这种情况下，误识别的可能性大大增加。由于当手持不同物体时，人手的肌肉信号是有所不同的，故肌电信号在人的任务识别中起着十分关键的作用。本文提出结合人的肌电信号辅助任务识别，采用加拿大Thalmic Labs公司推出的Myo腕带，其配备的肌电信号传感器可探测佩戴者对应的8处肌肉产生的电活动。

本文中通过对任务进行示范的方式，使机器人学习不同任务的协作技能，以协作人类完成任务。本文中记录机器人的末端位姿和人的位姿及肌电信号，并以此作为交互概率模型的训练样本，其中人机协作的不同任务示范如图2所示。

2 交互概率模型

由于在人机协作任务中，人和机器人在每次的协作中其运动不总是一成不变的，所以如果要对协作任务进行一般性的描述，则需要捕获任务过程中两者运动的时空差异性。下文对运动的空间差异性和时间差异性进行建模，并将其统一到交互概率模型中，以对人机协作任务进行描述。在人机协作的任务中，通过对人的状态的观测，对任务的类型进行识别，并基于训练得到的交互概率模型生成机器人的运动轨迹。为了提高任务的识别率，本文将肌电信号融入到该模型中，避免了错误的任务识别而造成的失败的机器人运动生成。

图2 人机协作的任务示范

2.1 运动的空间差异性建模

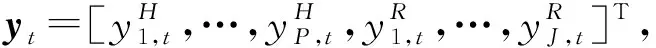
采用线性回归对单个训练样本进行描述，本文采用高斯基函数作为基函数，则其回归得到的概率形式的表达式为：

(1)

其中：Ht为时间步t的基函数矩阵，本文采用高斯基函数作为基函数；ω是对应的权重向量；Σy为零均值高斯噪声的协方差矩阵。

线性回归实质上是对运动轨迹进行参数化的过程，为了捕获运动的空间差异性，假设有：

p(ω|θ)=N(ω|μω，Σω).

(2)

其中：θ={μω，Σω}为权重向量ω的概率分布参数,μω和Σω分别为ω的高斯分布的均值和协方差矩阵。

基于yt的概率分布p(yt|ω)依赖于ω，而ω的概率分布p(ω|θ)又依赖于θ，由此可知，通过若干训练样本得到的时间步t上的运动分布p(yt|θ)符合层次贝叶斯模型(Hierarchical Bayesian Model，HBM)，如图3所示。

2.2 运动的时间差异性建模

由于每次任务示范中人手运动速度的不确定性，每个示范数据的时间长度是不尽相同的，因此有必要对运动进行时间上的对齐，并对时间差异性进行建模。

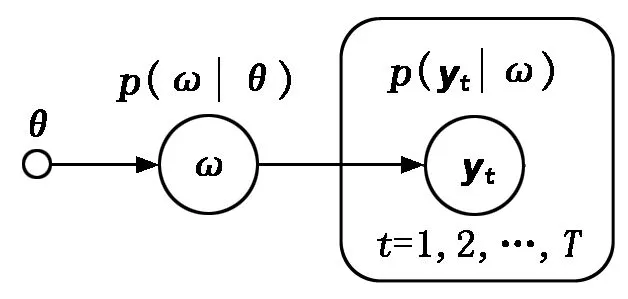
图3 层次贝叶斯模型

本文对所有训练样本在时间维度上进行线性缩放，使得所有训练样本的时长都为固定的名义时长Tnorm，从而使所有新的训练样本均完成了时间上的对齐。对于时长为T的训练样本，定义时长因子为：

α=T/Tnorm.

(3)

通过α的概率分布p(α)来描述运动的时间差异性，本文假设α服从高斯分布，即有：

(4)

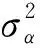
对于时长为α的训练样本，为实现将其在时间维度上进行线性缩放，在时间步上对基函数矩阵做时间维度的线性缩放得到新的基函数矩阵At，它与公式(1)中基函数矩阵Ht的关系为：

At=Hαt.

(5)

其中:Hαt表示时间步(αt)的基函数矩阵。

2.3 交互概率模型

图4为交互概率模型。

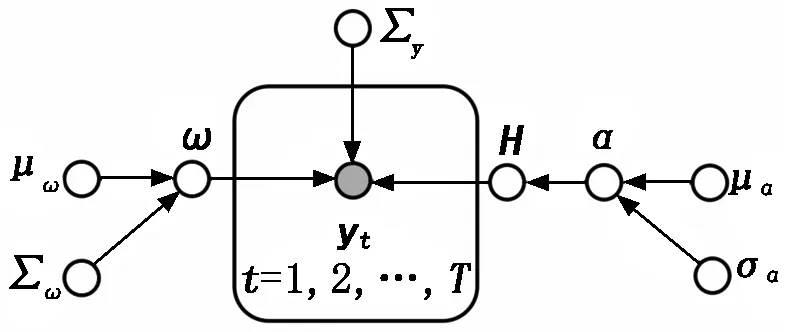
图4 交互概率模型

图4中，线性回归得到的参数ω的概率分布是对运动的空间差异性进行建模，时长因子α的概率分布是对运动的时间差异性进行建模，而对时间依赖的基函数矩阵A将时间和空间的差异性统一到一个概率模型中。

又由于p(yt|θ)符合HBM，故可通过边缘化ω得到时间t步下的运动状态y的概率分布：

(6)

其中：p(yt|ω，α)为yt在权重向量ω、时长因子α下的似然概率分布，且p(yt|ω，α)=N(yt|Atω，Σy)=N(yt|Hatω,Σy)。

2.4 任务识别与机器人轨迹生成

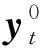
在K个任务的人机协作场景中，对所有任务模型分别估计其时长因子。具体的方法是通过最大后验估计，得到任务的时长因子为：

(7)

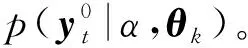
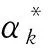
(8)

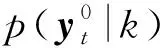
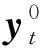
将y中表示机器人运动状态的部分取出，可得到机器人的运动轨迹，机器人通过执行该轨迹即可辅助人完成对应的任务。

2.5 融合肌电信号的交互概率模型

当人的运动在各个人机协作任务中的运动相似时，单纯地通过人的运动进行任务识别将会失效，而肌电信号对于人手持不同物体的场景十分地具有区分度。上述的模型对机器人和人的运动进行建模，本质上该模型讨论的是时间序列，故可把人的肌电信号级联到原来的状态向量中为:

(9)

其中：符号(·)EMG表示该数值属于测得的肌电信号。

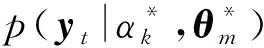
3 实验及分析

本文设置人机协作任务的实验，利用每个任务的示范获得若干的训练样本，对交互概率模型进行训练。在人机协作的测试场景中，采集人的运动和肌电信号，通过交互概率模型识别任务，并生成相应的机器人运动轨迹。

实验中，设置了3个不同的人机协作任务实验，如图2所示。在任务的示范过程中，利用ROS采集 Baxter机器人末端夹持器的运动，通过Xtion相机捕捉人手腕部的运动，以及用Myo腕带对人手腕部肌电信号进行读取，示范中记录得到的上述数据作为交互概率模型的训练样本。

通过设置对比实验分析肌电信号在人机协作任务中的重要性。在没有肌电信号的情况下，任务的平均识别率为49.2%，而在有肌电信号的情况下任务的平均识别率为85.8%。因此在任务的识别中，肌电信号起着十分显著的作用。

在完成任务识别后，通过若干人的运动状态的观测点，可生成机器人的运动轨迹，如图5所示。该轨迹与真实值基本吻合，证明了该模型下机器人轨迹泛化性能。

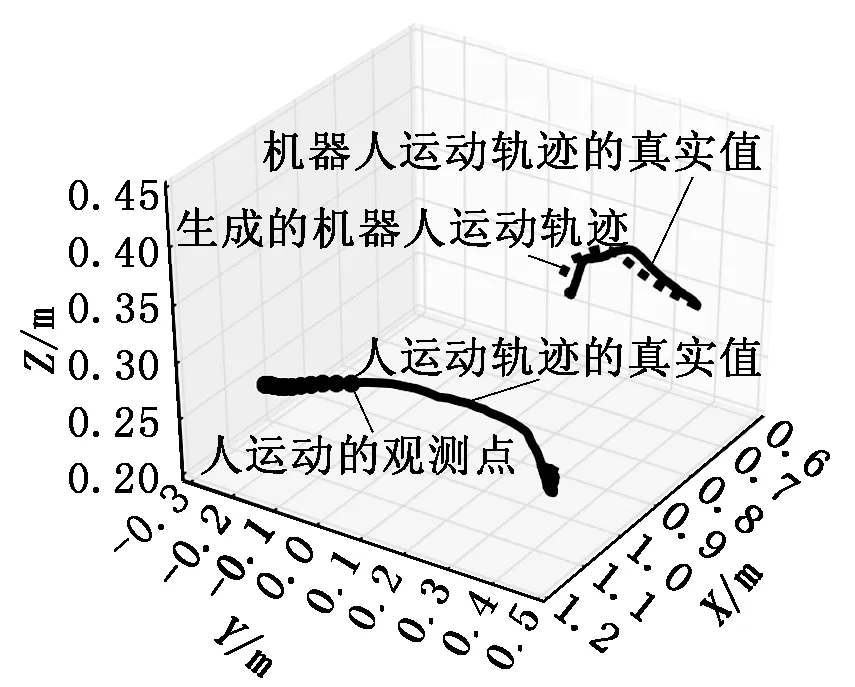
图5 机器人运动轨迹的生成

4 结束语

本文介绍了一种基于模仿学习的人机协作的任务建模方法，通过人工示范的方式，获得各个任务的训练样本。利用训练样本对交互概率模型进行训练，进而实现任务识别和机器人运动轨迹生成。本文将肌电信号级联到原来的运动状态向量中，大大地提高了任务的识别率，为后续的机器人运动轨迹生成奠定了基础。也证明利用交互概率模型对任务的时空差异性建模，具有十分强的泛化能力。