样条曲线构建优化技术的研究*

赵东宏　卢章平

(①江苏大学机械工程学院，江苏 镇江212013；②扬州工业职业技术学院，江苏 扬州 225127)



样条曲线构建优化技术的研究*

赵东宏①②卢章平①

(①江苏大学机械工程学院，江苏 镇江212013；②扬州工业职业技术学院，江苏 扬州 225127)

针对样条插值拟合精度差、光顺度不够理想的问题，开发适应性更好的样条曲线构建技术，其中“多段圆弧式光顺曲线”法吸收了圆弧曲率光顺的优点，与三次、五次样条插值后光顺的常用方式相比，“多段圆弧式光顺曲线”的曲率连续性好，逼近误差小，有效控制了数控加工中的刀轨波动；“桥接曲线光顺”法在保留桥接曲线操作方便优点的同时，显著提高了曲线的光顺度，在工业设计、逆向工程和数字化制造领域具有较大的实用价值。

自由曲面；样条插值；拟合精度；桥接曲线

在工业设计中，构建样条曲线是非常重要的基础性工作，如何以最小的逼近误差获得光顺的自由曲线是样条曲线拟合过程中的重点和难点问题[1-3]。

构建样条曲线有多种方法，如各种样条插值与逼近方法,用来拟合曲面的特征曲线(如边界曲线、截面曲线、轮廓曲线等)。目前主流的CAD软件中常用“通过点”、“根据极点”和“拟合样条”等方式构建样条曲线。其中“通过极点”无法精确通过已有的存在点，但容易获得曲率变化较小的光顺曲线，一般适用于正向概念设计；“通过点”是最基本的曲线拟合方式，可以很精确地通过存在点，但曲率变化通常比较剧烈；“拟合样条”自动化程度高但逼近误差偏大[4-6]。

本文以样条曲线为研究对象，针对样条插值拟合精度差、光顺度不够理想的常见问题，开发适应性更好的样条曲线构建技术。

1　样条曲线拟合方法的研究

1.1目前常用的曲线拟合法

1.1.1“通过点”曲线拟合

“通过点”是基本的曲线拟合方式，本文以空间复杂曲线(即样条曲率在数值和方向上的变化都比较大)为例进行研究。如图1所示的是最常用的三阶次“通过点”样条曲线，其逼近误差为0，但曲率变化波动大，曲率突变点较多。

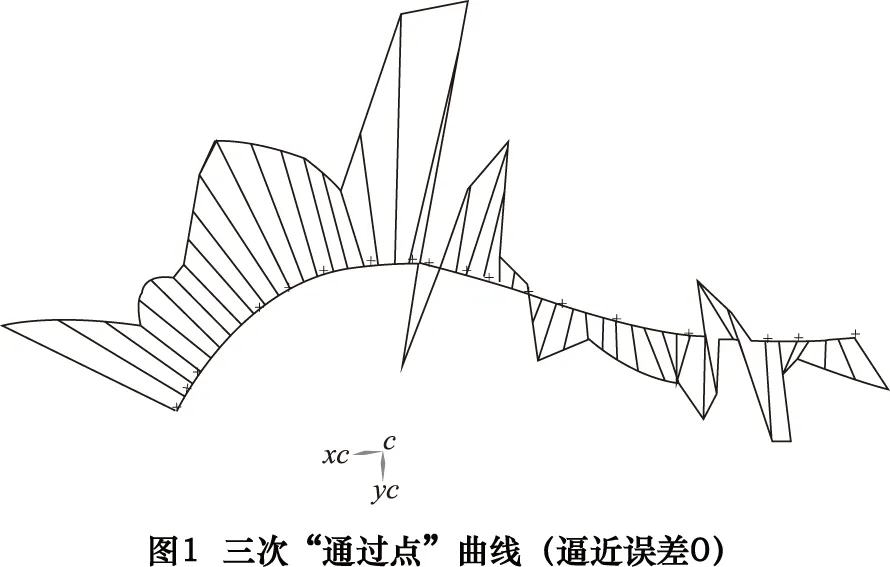
图2所示的是五阶次“通过点”样条曲线，曲率变化更加剧烈，曲线光顺度很差，在实际应用中价值不大。

1.1.2“过点光顺法”曲线拟合

在实际应用中为获得高质量的NURBS曲线，应该综合考虑曲线光顺度与逼近误差两方面的因素，因此主流CAD软件都有“光顺样条”功能，可以对“通过点”曲线进行后续的光顺优化，以增大逼近误差为代价改善样条曲线的光顺度，但在实践中存在曲线光顺后逼近误差比较大的问题。图3所示的是三次“通过点”曲线光顺后的曲率梳图，图4所示的是相对应的逼近误差测量值。

图5所示的是对五次“通过点”曲线光顺后的曲率梳图，图6所示的是逼近误差测量值。

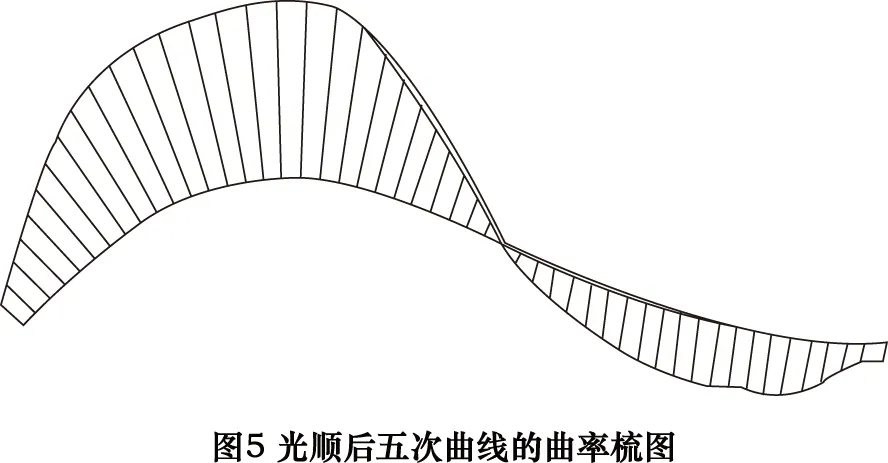
曲线阶次越大，形状越复杂，局部变化就越大。由曲线误差分析可知，相对三次曲线，五次曲线局部的曲率波动比较严重，曲线光顺需要更大的逼近误差。

由于阶次越大，曲线形状的控制难度也越大，工业设计中通常尽可能采用小阶次曲线如三次和五次样条，其中三次样条曲线算法简单、逼近误差小，应用非常广泛，而五次样条的优点是容易达到更高阶的连续性、更高的收敛性，目前在数控加工中的应用也越来越广泛[7-8]。

1.2多段圆弧式光顺曲线拟合法

由计算机图形学可知，样条曲线的曲率光顺度无法超过圆弧曲线，多段圆弧式光顺曲线吸收了圆弧曲率光顺的优点，采用分段拟合集中光顺的技术思路。具体的构建算法如下：

(1)如图7所示，将相邻三个插值点拟合为一段圆弧(在曲率平坦处单段圆弧的拟合点可多于三点)，可见每段圆弧的曲率变化非常光顺，但每段圆弧之间只能达到G0连续。

(2)如图8所示，对所有的圆弧曲线执行“光顺曲线串”命令，其中“连续性”选择G2，勾选“添加过渡圆角”，合并“所有曲线”即合并所有的小圆弧为单一曲线。

(3)在设置模块中勾选“高级曲线拟合”选项，在“方法”中选择 “样条次数与公差”，“次数”一般选择3次或5次，“最大偏差”应根据插值点的质量和分布情况选取，以能获得光顺曲线的最小偏差值为基准。本例中“最大偏差”选择0.25 mm即可获得光顺的样条曲线。

由以上测量和分析可知：与三次和五次样条相比，在达到相同光顺效果情况下，多段圆弧式光顺曲线在“最大距离误差”和“平均距离误差”等关键指标方面都有较大的优势，拟合精度明显提高(如表1所示)。

表1曲线拟合误差的对比

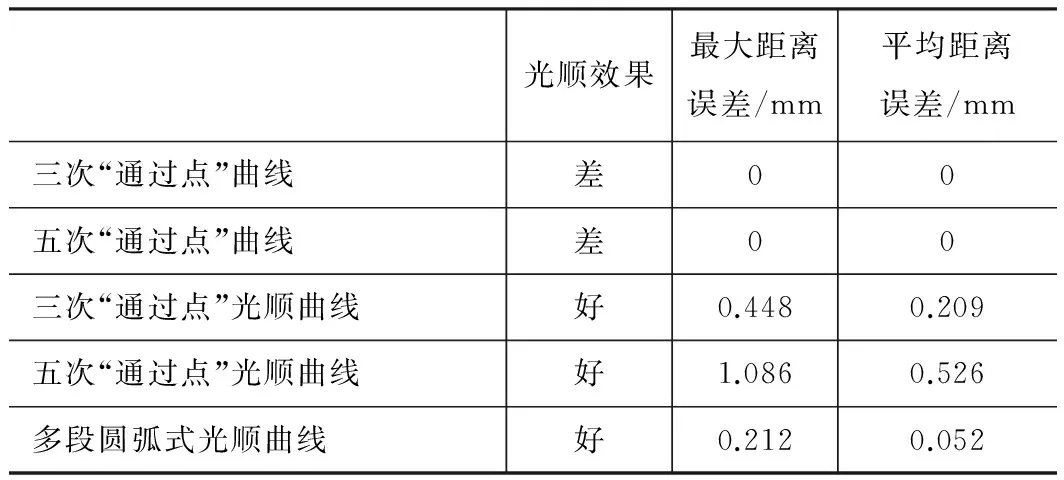
光顺效果最大距离误差/mm平均距离误差/mm三次“通过点”曲线差00五次“通过点”曲线差00三次“通过点”光顺曲线好0.4480.209五次“通过点”光顺曲线好1.0860.526多段圆弧式光顺曲线好0.2120.052

2　桥接曲线光顺技术

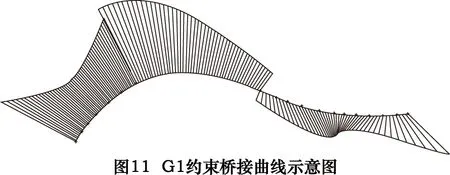
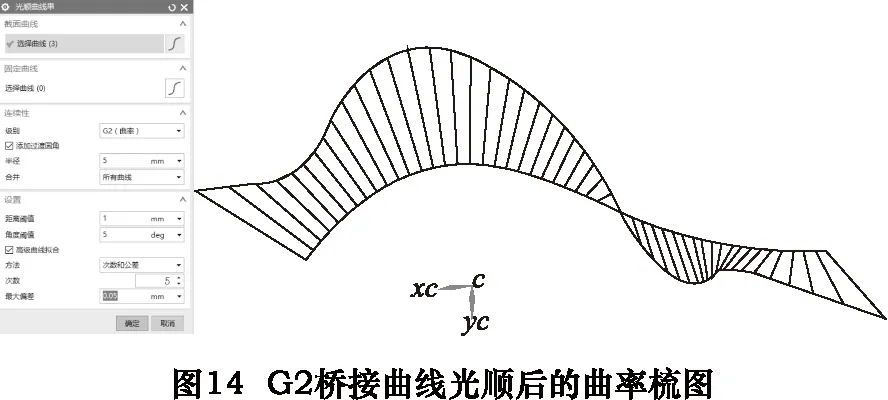
在曲面的构建过程中，两条曲线之间有间隙的情况很常见，“桥接曲线”命令可以很方便地创建两条曲线的连接曲线，并保证连接曲线与原来曲线之间的光顺性约束(G1，G2)。图11所示的是两条不相连样条曲线以G1约束桥接的情况，可见曲率不连续，曲线连接质量较差；图12所示的是以G2约束桥接的情况，显然G2桥接曲线质量较高，但就整体而言曲线的光顺度仍不够理想，这种情况在桥接曲线过程中非常普遍，直接影响了曲线的拟合质量。

为解决这一曲线拟合过程中的瓶颈问题，对图11中的三段曲线执行图8中的“光顺曲线串”命令，在“最大偏差”设置为0.15 mm时，可获得图13所示的光顺拟合曲线。

对图12中的三段曲线执行“光顺曲线串”命令，当“最大偏差”设置为0.05 mm时，即可获得光顺的拟合曲线(图14所示)，显然对“光顺曲线串”命令而言，原始曲线质量越好，其光顺误差也越小。

3　结语

(1)样条曲线构建是自由曲面设计中的难点问题，针对样条插值拟合精度差、光顺度不够理想的问题，提出了“多段圆弧式光顺曲线”，吸收了圆弧曲率光顺的优点，与三次、五次样条插值后光顺的常用方式相比，“多段圆弧式光顺曲线”连续性好，逼近误差小，有效控制了数控加工中的刀轨波动。

(2)“桥接曲线光顺”法在保留“桥接曲线”操作方便优点的同时，显著提高了样条曲线整体的光顺度，为曲线之间的光顺过渡提供了新的手段。

(3)通过几百个不同类型复杂曲线的软件模拟，结果证明“多段圆弧式光顺曲线”法和“桥接曲线光顺”法能有效提高样条曲线的拟合精度和光顺度，在工业设计、逆向工程和数字化制造领域具有较大的实用价值。

[1]江本赤，韩江，夏链．B样条曲线逼近偏差的精确求解算法[J]．制造技术与机床，2015(7)：67-71.

[2] Les Piegl,Wayne Tiller．非均匀有理B样条[M].北京：清华大学出版社，2010.

[3] 徐进，柯映林，曲巍崴 . 基于特征点自动识别的B样条曲线逼近技术 [J]. 机械工程学报, 2009,45(11)：212-217.

[4] 程仙国，刘伟军，张鸣 . 特征点的B样条曲线逼近技术 [J]. 计算机辅助设计与图形学学报, 2011,23(10)：1714-1718.

[5] Piecl L A，Tiller W . Least-square B-spline curve approximation with arbitrary end derivatives [J]Engineering with Computers, 2000,16(2)：109-116.

[6] 赵世田，赵东标，付莹莹 . 测量数据点的高精度B样条曲线拟合算法[J].计算机集成制造系统，2010，16(8)：1714-1718．

[7]王烈，廖小平.基于矩阵的NURBS曲线建模及其生成算法[J]．现代制造工程，2007(2)：31-33．

[8]田锡天，杨海成.Fichtner 五次插值样条在NC过程链中的应用研究[J]．机械科学与技术，2002，23(11)：75-77.

(编辑谭弘颖)

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Study on spline curve constructing optimization technology

ZHAO Donghong①②,LU Zhangping①

(①School of Mechanical Engineering,Jiangsu University,Zhenjiang 212013,CHN; ②Yangzhou Polytechnic Institute,Yangzhou 225127,CHN)

This paper is against the issue on poor fitting accuracy and insufficient smoothness of spline fitting. More adaptive spline curve constructing technology is developed, of which "multi-arced smooth curve" merges the advantage of arc curvature fairing. Compared with common fairing after cubic or quintic spline interpolation, "multi-arced smooth curve" has more curvature continuity and less approximation error and effectively control the tool path fluctuation during CNC machining. "Bridging smooth curve" not only makes bridging curve easy to operate, but also significantly improves the smoothness of the curve. In industrial design, reverse engineering and digital manufacturing, the method has great practical value.

freeform； spline interpolation；fitting accuracy；bridging curve

TH164

A

10.19287/j.cnki.1005-2402.2016.08.011

赵东宏，男，1967年生，博士生，副教授、高级工程师，长期从事数字化设计与制造方面的工作，在工业设计和软件编程方面具有多年一线工作经验，已发表专业论文十余篇，拥有发明专利6项和实用新型专利6项。

2016-03-29)

160822

* 教育部博士点基金项目: “基于意向认识的产品创新设计与评价方法研究”( 20113227110007)