变速箱同步器齿毂挤齿加工工艺仿真分析
张学忱 王 风 李占国② 史尧臣②
(①长春理工大学机电工程学院,吉林 长春 130022;②长春大学机械工程学院,吉林 长春 130022)
变速箱同步器齿毂挤齿加工工艺仿真分析
张学忱①王风①李占国①②史尧臣①②
(①长春理工大学机电工程学院,吉林 长春 130022;②长春大学机械工程学院,吉林 长春 130022)
针对中型卡车变速箱同步器齿毂齿面减薄加工要求,采用挤齿加工方法。基于滑移线场方法求解了齿毂挤齿加工过程中齿面应力,利用ANSYS瞬态动力学模块对齿毂挤齿成形过程进行动力学仿真分析,得到了挤齿加工过程中的齿面应力、应变分布,并系统研究了挤齿力和转速对齿毂齿面应变的影响规律,为同步器齿毂挤齿加工工艺研究提供了理论依据和仿真分析方法。
同步器齿毂;挤齿加工工艺;仿真分析
同步器齿毂是变速箱中的关键部件,作用是在汽车变速换挡时,使转速不等的两个齿轮在达到相同转速时进行相互啮合,使换挡过程更加平顺方便,减缓换挡过程中齿轮间的碰撞冲击。因此,将同步器齿毂的工作表面进行减薄处理来达到顺畅啮合的作用[1]。齿毂减薄加工工艺可采用插齿法、铣齿法、挤齿法等加工工艺,插齿法加工精度比较高,但是应用此方法会产生毛刺翻边问题,影响产品的质量与精度;铣齿法加工出的工件精度较低,粗糙度较差,很难保证同步器齿毂工作时正常运行;挤齿法也称精挤齿或齿轮的精整加工,它是一种将挤轮(滚模)与工件(经过滚齿或插齿粗加工的齿轮)施加径向力后强制啮合的加工方法,属于近净成形技术,其优点主要是生产率高、成本低,无切屑,加工后的齿面粗糙度较好[2]。所以同步器齿毂采用挤齿加工方法。
目前国内外对挤齿加工技术进行了一系列的试验与研究。2008年王明福、付建华等人对花键轴挤齿加工过程进行了理论分析,研究了花键轴挤齿成形过程中金属流动规律,并利用DEFORM软件对花键轴挤齿成形过程进行了数值模拟。最终得出挤齿加工出的工件表面粗糙度可达Ra0.3 μm[3]。目前,美国的KINEFAC CORPORATION公司已研制出可加工模数为3 mm,压力角为30°的花键轴三轮挤齿机[4]。
1 齿毂挤齿塑性成形原理
在齿毂(工件)挤齿加工过程中,应用两个齿轮的啮合原理,对挤轮施加恒定的径向力使工件与挤轮强制啮合,进而使工件齿面产生塑性变形以达到加工目的。求解金属材料塑性变形的方法有:滑移线场法、初等解析法、上限法等[5]。滑移线场法在计算塑性材料应力应变问题时,有助于建立更符合实际情况的挤齿模型,它在数学上比较严谨、理论计算上比较完整,计算精度也较高[6]。
挤齿加工过程中,挤轮齿廓与工件齿廓接触区域发生塑性变形,设z轴为工件的轴线方向,y轴为挤轮中心与挤轮齿顶齿宽中点连线方向,x轴则为与两轴均垂直的方向,y′轴为齿面法线方向。
挤齿加工时,工件与挤轮齿侧渐开线接触,在此接触区域内可简化为两圆柱体的接触形式。本文同步器齿毂为正变位的短齿齿形,因此,以齿毂(工件)与挤轮啮合挤齿时刻的节圆与渐开线齿廓交点处的切线AB替代工件齿廓渐开线来简化接触区域,工件齿部不接触的自由边界将其简化为直线BC。由各区域的边界条件可绘制挤齿时的滑移线场如图1所示。
在滑移线场ABE中,其滑移线为直线场;在滑移线场BDE中,其滑移线为扇形场;滑移线场BCD为自由边界的滑移线场。
在自由边界BC取一点b,AB边界取一点a,并保证a、b两点在同一条滑移线上。根据滑移线性质可知,ba线为β线,ae线为α线。a、b两点的应力图如图2所示,a点最大切应力方向与接触面成φa角,y′轴方向的应力及切应力分别为σy′、τx′y′;b点最大切应力方向与自由表面成ωb角,其第一与第三主应力分别为σb1、σb3。

挤齿时接触区域的摩擦条件符合库伦摩擦定律,且摩擦系数μ满足条件:
(1)
式中:φa为a点滑移线与接触面夹角;α为压力角。
由式(1)可得出a点的滑移线与接触面夹角与摩擦系数μ的关系。
a点的滑移线方向角ωa为
(2)
根据亨盖应力方程得出a点的平均应力σma为
σma=σmb-2K(ωa-ωb)
(3)
式中:σmb为b点平均应力;ωb为b点滑移线方向角;K为最大切应力。
b点处符合自由边界条件,所以:
(4)
式中:σb1为b点第一主应力。
由屈雷斯加屈服准则可得b点第三主应力σb3为
σb3=-2K
则b点的平均应力σmb为
(5)
由式(3)及式(5)整理得:
(6)
在工件与挤轮接触区:
(7)
式中:σy′为沿y′轴方向齿面应力;Fn为沿y′轴方向所受的力;Fr为径向力;A为接触面积。
由此可得x′方向的应力σx′为:
σx′=2σma-σy′
(8)
2 同步器齿毂挤齿加工过程仿真分析
2.1同步器齿毂与挤轮三维模型建立
挤齿加工过程中,使齿毂工作表面的齿厚减薄0.25~0.35 mm,沿齿宽方向保留原长度15.7±0.2 mm。加工参数如图3所示。
同步器齿毂与挤轮的各项参数如表1所示。
利用CATIA软件建立齿毂与挤轮的三维模型,导入到ANSYS软件中,如图4所示。
表1齿毂与挤轮参数表

齿毂挤轮模数/mm2.52.5齿数4049压力角/(°)2020齿顶圆直径/mm104.5123.46齿根圆直径/mm99115.2变位系数+0.80

2.2材料设置
设定齿毂材料为20CrMnTi,密度为7 800 kg/m3,杨氏模量207 GPa,泊松比0.25,屈服极限835 MPa,切变模量80 GPa。挤轮材料为高速钢,施加材料的密度为7 850 kg/m3,杨氏模量300 GPa,泊松比0.3,屈服极限2 000 MPa,切变模量90 GPa。
2.3网格划分
网格划分采用multiple多域扫略方法,网格为六面体,单元大小设为1 mm,单元数为261 886个,节点数为1147 978个,轮齿网格如图5所示。

2.4施加约束条件、载荷及时间步
模拟实际工况,齿毂(工件)为主动轮,挤轮为从动轮,在挤轮端面处施加径向挤齿力,使挤轮齿面与齿毂齿面接触,在挤压力的作用下,使齿毂齿面产生塑性变形。
仿真中,限制同步器齿毂(工件)沿x、y、z方向的移动及绕x、y轴的转动;限制挤轮沿y、z方向的移动及绕x、y轴的转动。设定载荷步时,在Analysis settings中设定时间步为3步,每一步的参数设置如表2所示。
表2参数设置表

时间/s挤齿力/kN转速/(r/min)一步0~10~700~250二步1~270250三步2~2.570~0250~0
2.5仿真结果分析
当挤齿力为70 kN时,齿面所受的最大应力为4 648.8 MPa,如图6所示;齿面产生的最大塑性变形为0.029 807 mm,如图7所示;应用于实际加工中同步器齿毂(工件)转9~11转即可达到加工要求。


(1)挤齿力对塑性变形的影响分析
当齿毂(工件)转速为250 r/min,挤齿力分别为30 kN、50 kN、70 kN时。同步器齿毂齿面处的塑性变形动态曲线如图8所示,当挤齿力为70 kN时,最大塑性变形量为0.029 807 mm,当挤齿力为50 kN时,最大塑性变形量为0.019 898 mm,当挤齿力为30 kN时,最大塑性变形量为0.013 004 mm。
取仿真中一个挤齿周期齿毂单个齿面的塑性变形量,如图9所示,单个齿由啮合到脱开的时间为0.006 s,当齿毂齿面刚进入啮合区域,挤齿力为30 kN时齿面的塑性变形量为0.003 47 mm,挤齿力为50 kN时齿面的塑性变形量为0.004 69 mm,挤齿力为70 kN时齿面的塑性变形量为0.00 573 mm;当齿毂齿面完全进入啮合区域,挤齿力为30 kN时齿面的塑性变形量为0.011 5 mm,挤齿力为50 kN时齿面的塑性变形量为0.015 8 mm,挤齿力为70 kN时齿面的塑性变形量为0.024 4 mm;当齿毂齿面即将脱离啮合区域,挤齿力为30 kN时齿面的塑性变形量为0.004 27 mm,挤齿力为50 kN时齿面的塑性变形量为0.005 35 mm,挤齿力为70 kN时齿面的塑性变形量为0.007 48 mm。可看出齿毂齿面由开始啮合到脱离的过程中,其齿面塑性变形量先逐渐增大,然后逐渐减小,此规律符合齿轮啮合传动规律。并由仿真数据可得出同步器齿毂齿面的塑性变形量随挤齿力的增加而增大。


(2)转速对塑性变形的影响分析
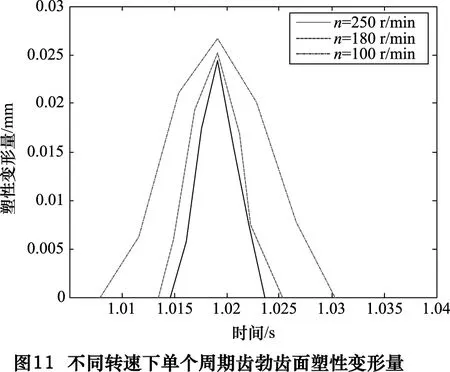
当挤齿力为70 kN,转速分别为100 r/min、180 r/min、250 r/min时,齿毂齿面处的塑性变形动态曲线如图10所示。当转速为100 r/min时,最大塑性变形量为0.034 229 mm;当转速为180 r/min时,最大塑性变形量为0.031 mm;当转速为250 r/min时,最大塑性变形量为0.029 807 mm。

取仿真中一个挤齿周期齿毂单个齿面的塑性变形量,如图11所示。由图可看出此时齿毂齿面塑性变形规律同样符合齿轮啮合传动规律。由仿真数据可得,齿毂齿面的塑性变形量随转速的增加而逐渐减小。
3 结语
本文针对中型卡车变速箱同步器齿毂塑性成形技术,采用齿毂挤齿加工方法。并对齿毂挤齿加工过程进行了如下研究:
(1)基于滑移线场法建立了齿毂挤齿加工过程时齿面应力的计算方法。
(2)应用CATIA软件建立了同步器齿毂与挤轮的三维模型,应用ANSYS瞬态动力学对齿毂挤齿加工过程进行动力学仿真分析,得出齿毂挤齿过程中齿面应力及塑性变形分布云图。
(3)通过仿真分析得到了挤齿力、转速对齿毂齿面塑性变形的影响规律。当转速为250 r/min,挤齿力分别为30 kN、50 kN、70 kN时,齿毂齿面塑性变形量随挤齿力的增加而增大;当挤齿力为70 kN,转速分别为100 r/min、180 r/min、250 r/min时,齿毂齿面塑性变形量随转速的增加而减小。
[1] 郭增刚,吴宗利. 新一代同步器开发与应用[J]. 汽车工程师,2011(2):58-60.
[2] 李延斌,郑鹏. 硬齿面齿轮精密热滚挤加工方法[J]. 沈阳工业大学学报,2002,24(6):457-460.
[3] 王明福,付建华. 花键冷滚压成形过程有限元分析[J].锻压技术,2010,35(4):155-159.
[4] 聂兰启. 谈谈国内花键轴轴向挤压的发展方向[J]. 精密成形工程,2013(1):41-46.
[5] 倪坤. 弧形刻刀的主刃半径对中阶梯光栅槽型的影响研究[J]. 现代制造工程,2011(1):74-77.
[6] 秦小琼,刘德学. 杯形件反挤压变形力的滑移线场数值分析解[J]. 山东大学学报, 2011(12):67-69.
(编辑汪艺)
如果您想发表对本文的看法,请将文章编号填入读者意见调查表中的相应位置。
Gear extrusion machining process simulation analysis of gearbox synchronizer gear hub
ZHANG Xuechen①, WANG Feng①, LI Zhanguo①②, SHI Yaochen①②
(①College of Mechanical and Electrical Engineering, Changchun University of Science and Technology, Changchun 130022, CHN;②College of Mechanical Engineering, Changchun University, Changchun 130022, CHN)
For medium truck gearbox synchronizer gear hub tooth thinning processing requirements, the idea of extrusion processing is put, and based on the slip line field method, the gear hub tooth surface stress of technical process is solved. The dynamic analysis of the gear hub tooth profile precision molding process is made by the ANSYS transient dynamics module, the tooth surface stress and strain distribution in the extrusion process are obtained, and the influence law of gear extruding force and speed on the tooth surface of the gear hub strain is studied, and provides the theoretical basis and the simulation analysis method for synchronizer gear hub crowded teeth processing technology research.
synchronizer gear hub; tooth crowded processing; simulation analysis
TG376.3
A
10.19287/j.cnki.1005-2402.2016.08.005
张学忱,女,1963年生,博士,教授,研究方向为机械精密加工技术、数字化设计与制造。
2016-01-26)
160816

