双轮错距缩径旋压力测量平台设计*
吴 磊 刘 彬
(①中山火炬职业技术学院装备制造系,广东 中山 528437;②华南理工大学机械与汽车工程学院,广东 广州 510641)
双轮错距缩径旋压力测量平台设计*
吴磊①刘彬②
(①中山火炬职业技术学院装备制造系,广东 中山 528437;②华南理工大学机械与汽车工程学院,广东 广州 510641)
为了提高加工效率,提出了双轮错距缩径旋压工艺。采用八角环测力计测量了旋压三向力,设计并通过理论计算验证了八角环测力计的准确性;通过应变分析,设计了应变片的贴片位置。在不同加工参数下,利用动态应变仪及八角环测力计对三向旋压力进行测定,对试验数据进行滤波处理,并最终得到三向旋压力的数据。
错距缩径旋压;旋压力;八角环
目前,缩径旋压是单一旋轮进行加工[1-2],当加工直径变化较大的毛坯时,由于直径单次变化过大会引起毛坯加工缺陷[3-4],因而往往需要规划旋轮的加工路径,分多道次加工完成,其加工效率会相对较低。为了提高加工效率,借鉴用于强力旋压的错距旋压[5-6],本文提出双轮错距缩径旋压工艺。双轮错距缩径旋压工艺加工示意如图1所示,毛坯在主轴夹头的夹持下高速旋转,旋轮在轴向错位,分为前旋轮和后旋轮,相对于后旋轮,前旋轮的径向进给量较小,两个旋轮沿轴向同时同速度进给,因而可以在一道次完成两个下压量,是单轮旋压工作效率的两倍,该旋压工艺可以有效地提高旋压效率。
旋压力是工程设计人员旋压机结构设计以及电动机选型的重要参数[7-8]。旋压力属于三向力,需要使用三向测力计。目前市面上的三向测力计为压电式三向测力计,其主要应用于车削力的测量[9-10],成本高昂且若应用于旋压力的测量还需设计结构将旋轮安装于测力计上。

文献[11]给出了利用八角环测量三向力的方法,该方法结构简单,成本低。本文在前人的基础上结合双轮错距旋压工艺特点设计试验平台。
1 平台设计
平台设计如图2所示,平台在车床的拖板平面上增加一组十字平台组件,及八角环传感器,十字平台可以微调轴向和径向的旋压错距。假设旋轮受到的径向力、摩擦力、轴向力分别F、f、P。为了方便计算八角环的受力,将径向力设计在八角环的对称面上,假设旋压接触面到八角环上半部分中性面的距离为l1,旋压接触面到八角环中间对称面的距离为l2,如图2所示。

2 八角环传感器受力应变分析
八角环是根据圆环在受力时存在应变节点的原理设计的,尺寸参数如图3所示,其中,r为八角环的等效半径。

2.1八角环传感器受径向力及轴向力的应变分析
对该八角环的受力分析可以等效成圆环的受力分析,由于八角环受到径向力、轴向力、摩擦力作用在各截面时,其所产生的截面应力是相同的,即应变相同,因此只考虑各力在截面处产生的弯矩。又由于径向力产生的弯矩与轴向力产生的弯矩在同一平面内,而摩擦力产生的弯矩与前两者垂直,因此分析前两者产生的应变时,可以忽略摩擦力的影响。先分析各截面受径向力与轴向力产生的弯矩作用下的应变。先忽略轴向力等效时产生的弯矩,当八角环受到径向力和轴向力作用时,该结构的受力分析如图4所示。

假设圆环某一截面与竖直方向的夹角为θ,根据该结构的受力为超静定结构,各文献均已给出在单独的径向力F或轴向力P作用时,圆环的截面所受到的弯矩为:
(1)
Mθ P= 0.5Prcosθ
(2)
因此当θ为39.5°时,F产生的弯矩为零,当为90°时,P产生的弯矩为零。但由于此圆环是由八角环等效而成,文献[11]指出八角环结构满足r/L=0.4时,θ为45°时,F产生的弯矩才为零。目前的八角环测力原理大都是根据上述公式进行贴片,但是该结构的尺寸要求比较严格。现根据本实验装置的结构特点,推导分析公式,从而提出另一种测力方案。
当图2的受力情况向图4的受力情况简化时,轴向力P的等效忽略了产生的弯矩,因此需要额外再增加弯矩这一选项。现对该弯矩单独作用在此结构进行受力分析,如图5a所示。由于结构对称,且加载的外载荷反对称,因此,该结构受力可以简化为图5b。其中I1为八角环弧线部分的惯性矩,I2为八角环直线部分的惯性矩,根据本次尺寸设计得到I2=16I1。

弯矩MP的大小为:
MP=Pl1
(3)
根据力平衡方程可以得到:
FA=X1
(4)
MA=MP/2+X1L
(5)
因此AB段截面受到的弯矩如下:
BC段截面受到的弯矩:
卡式定理得:
(6)
由式(6)得到:
其中,K=L/r,本次结构设计,取K=2。因此,AB段截面受到的弯矩为:
(7)
故由式(1)、(7)得:
在AB段,θ为90°的截面外沿线:
F产生的应变:
(8)
P产生的应变:
(9)
在AB段,θ为90°的截面内沿线应变与内沿线相应力产生的应变符号相反。
在AB段,θ为45°的截面外沿线:
F产生的应变:
(10)
P产生的应变:
(11)
在AB段,θ为135°的截面外沿线:
F产生的应变:
(12)
P产生的应变:
(13)
由此,根据式(8)~(13),通过在相应的位置合理地布置应变片即可求出相应的力。
2.2八角环传感器受摩擦力的应变分析
摩擦力与轴向力和径向力垂直,选取的应变测试点与前两者应变测试点的选取原则相同,应选取为八角环中间部分的上下端点。这样可以尽可能地减小轴向力和径向力的影响。八角环传感器受摩擦力的应变可以等效成一个梁受到摩擦力的应变。其中八角环中间部分的惯性矩为:
(14)
摩擦力弯矩在八角环中间部分上下两端产生的应变为:
(15)
3 八角环传感器贴片位置及电路设计
八角环传感器贴片位置如图6所示。

由于各应变点所在截面的轴向应力产生的应变相同且很小可以忽略不计,因此,在设计电桥时忽略轴向应力产生的应变,各点由于弯矩产生的应变如表1所示。
表1各点受弯矩产生的应变

测试点F产生的应变P产生的应变f产生的应变总应变1εF90εP900εF90+εP902-εF90-εP900-εF90-εP903εF90εP900εF90-εP904-εF90-εP900-εF90+εP905εF90εP900εF90+εP906-εF90-εP900-εF90-εP907εF90εP900εF90-εP908-εF90-εP900-εF90+εP90900εfεf1000εfεf1100-εf-εf1200-εf-εf13εF45εP450εF45+εP4514εF45-εP450εF45-εP4515εF135εP1350εF135+εP13516εF135-εP1350εF135-εP13517εF45εP450εF45+εP4518εF45-εP450εF45-εP4519εF135εP1350εF135+εP13520εF135-εP1350εF135-εP135
根据表1可以设计出图7所示电路,采用全桥电路。

其中图7a测出F产生的应变εF与相应力的关系,从而测出力F;图7b测出P产生的应变εMP与相应力的关系,从而测出力P;图7c测出f产生的应变εf与相应力的关系,从而测出力f。
4 八角环传感器的标定
为了更加准确地知道八角环所测的力学数据,需要对其进行标定。针对3个方向的受力载荷大小,分别采用不同的方式进行标定。
根据旋轮所受径向力的方向以及位置,八角环径向力标定实物图如图8a所示,拉伸机所施加的压缩力通过铜柱传递至八角环。通过施加不同载荷采集,进行拟合的数据结果如图8b所示。
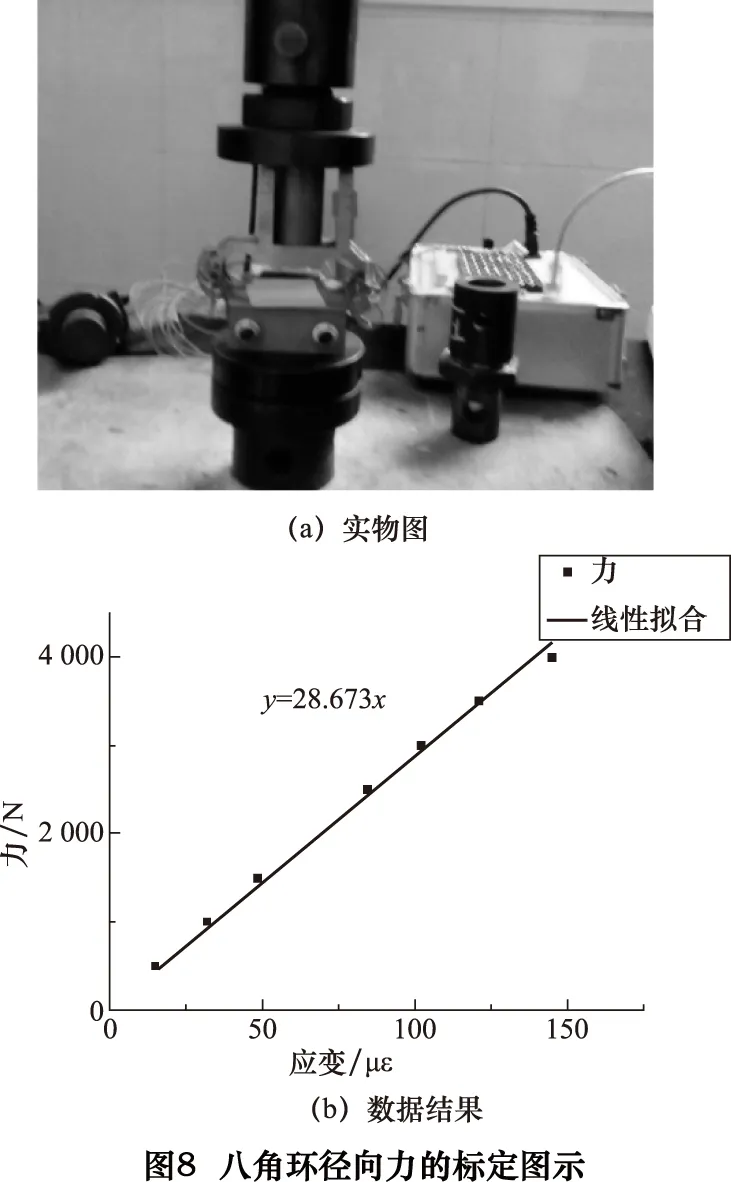
与径向力标定类似,根据旋轮所受轴向力的方向以及位置,依次施加载荷对八角环标定。八角环所受旋压轴向力、切向力与桥路输出应变的数据采集结果分别如图9、图10所示。


5 试验数据处理与结果
5.1试验数据处理
试验过程中,由于机床的振动会带动八角环的振动,从而影响数据的采集。如图11所示,为应力应变仪在50 Hz的采集频率下采集到的径向力随时间变化点。由于多种振动信号的干扰,无法在此原始数据中读取准确的旋压力,因此需要进一步的数据处理。此次数据采集由于受到机床高频率振动信号的影响,因此需要利用Origin进行过滤。

最终经过低频滤波器处理后数据曲线如图12所示。根据加工阶段,可以将全程分为五个阶段:阶段Ⅰ由于旋轮未与管坯接触,旋压力为零,阶段Ⅱ旋轮与管坯开始接触,并且随着进给量的增大,接触部分缓慢增多,因此旋压力也从零开始逐渐增大;阶段Ⅲ旋轮与管坯的接触面积增加到大最大值,此时旋压力基本保持不变,此时读数即为所测旋压力;阶段Ⅳ旋轮逐渐远离管坯,旋压力逐渐减小;阶段Ⅴ旋轮与管坯完全脱离,因此旋压力恢复至零。
其他两个方向的旋压力与径向力数据的处理方法相同,因此不再赘述。
5.2试验数据结果与分析
对不同工艺参数下的三向旋压力进行测量,试验的管坯为紫铜管,外径28 mm,壁厚1.2 mm,分别对单旋轮旋压时的轴向进给量、径向进给量、主轴转速,双旋轮错距旋压时的径向进给量、轴向错距量等对旋压力的影响进行了测量,具体如下:

(1)单旋轮旋压时,轴向进给量设定为0.394 mm/r,径向进给量设定为1 mm,在不同转速下,三向旋压力试验结果如图13所示。

从试验测量数据看,在不同转速、同一轴向进给量、径向进给量的条件下,其三向力的幅值变化不大,基本保持恒定。这表明在轴向进给量恒定的前提下,三向旋压力的大小与管坯转速无关。
(2)单旋轮旋压时,轴向进给量设定为0.394 mm/r,转速恒为375 r/min,在不同径向进给量下,三向旋压力的变化情况,如图14所示。

图14表明三向旋压力均随径向进给量的增加而增大,三向力的关系为:径向力>轴向力>切向力。
(3)单旋轮旋压时,径向进给量设定为1 mm,转速恒为375 r/min,在不同轴向进给量下,三向旋压力的变化情况,如图15所示。
图15表明三向旋压力均随轴向进给量的增加而增大,三向力的关系亦为:径向力>轴向力>切向力。

(4)双轮错距旋压时,轴向错距量恒为4 mm,轴向进给量为0.394 mm/r,转速恒为375 r/min,两旋轮的总的径向进给量为2 mm,在不同前轮径向进给量下,前后两旋轮三向旋压力的变化情况,如图16所示。

在总的径向进给一定的前提下,图16表明,前轮的三向旋压力随着前轮径向进给量的增加而增大,后轮的三向旋压力随着前轮径向进给量的增加而减小。
6 结语
(1)由于单轮缩径旋压加工效率较低,本文提出了双轮错距缩径旋压工艺,并采用八角环测力计测量了旋压三向力。设计并通过理论计算验证了八角环测力计的准确性,通过应变分析,设计了应变片的贴片位置。
(2)在不同加工参数下,利用动态应变仪及八角环测力计对三向旋压力进行测定,对试验数据进行滤波处理,并最终得到三向旋压力的数据。从测量数据来看,可以得出如下结果:①旋压三向力关系如下,径向力>轴向力>切向力;②在轴向进给量恒定的前提下,旋压力基本不会随着管坯转速的变化而变化;③旋压力随着径向进给量、轴向进给速度的增加而增大;④在总的径向进给一定的前提下,前轮的三向旋压力随着前轮径向进给量的增加而增大,后轮的三向旋压力随着前轮径向进给量的增加而减小。
[1]程秀全, 陈家华, 夏琴香. 无芯模缩径旋压力的有限元数值模拟及试验研究 [J]. 塑性工程学报, 2007,14(5):38-42,47.
[2]王锋. 无模缩径旋压工艺的力学分析与数值模拟 [D].西安:西北工业大学, 1999.
[3]Iguchi T, Yoshitake A, Irie T, et al. Numerical simulation and development of tube spinning process for exhaust system components of motor vehicles[C].Proceedings of the Materials Processing & Design: Modeling, Simu, F, 2004.
[4]Ge T, Wang J, Lu G-D, et al. A study of influence of interference phenomenon on stagger spinning of thin-walled tube [J]. P I Mech Eng B-j Eng, 2014:1-19.
[5]李永华, 张宁, 檀雯. 不锈钢筒形件错距旋压过程的缺陷研究[J].锻压技术, 2009,34(6): 32-34,58.
[6]夏琴香, 张鹏, 程秀全. 筒形件错距旋压成形工艺参数的正交试验研究[J].锻压技术, 2012(6): 42-46.
[7]程秀全, 许业华, 夏琴香. 框架式三旋轮错距旋压成形装置的研制[J].锻压装备与制造技术, 2005(6): 31-35.
[8]赵升吨, 赵承伟, 王君峰. 现代旋压设备发展趋势的探讨[J].中国机械工程, 2012(10): 1251-1255.
[9]张铁. 三向压电式车削测力仪的性能研究与结构设计[D].大连:大连理工大学, 2007.
[10]尚永艳. 刀柄式压电切削测力仪研究 [D].大连:大连理工大学, 2014.
[11]王成和, 刘克璋. 旋压技术 [M].北京; 机械工业出版社,1986.
(编辑孙德茂)
如果您想发表对本文的看法,请将文章编号填入读者意见调查表中的相应位置。
Design for measurement of spinning force on stagger neck-spinning with double rollers
WU Lei①, LIU Bin②
(①Equipment Manufacturing Department, Zhongshan Torch Polytechnic, Zhongshan 528437, CHN; ②School of Mechanical & Automotive Engineering, South China University of Technology, Guangzhou 510641, CHN)
To improve the efficiency, stagger neck-spinning with double rollers is presented in this paper. An octagonal ring transducer is designed for measuring the spinning forces in three directions. The validity of the octagonal ring was verified by the theoretical calculations, and the positions of strain gauges were designed by strain analysis. The spinning force in different process parameters was measured by octagonal ring transducers and a dynamic stress-strain instrument. The data of forces was obtained after filtering.
stagger neck-spinning; spinning force; octagonal ring
TG3
A
10.19287/j.cnki.1005-2402.2016.08.009
吴磊,男,1979年生,研究生,副教授,主要从事CAD/CAM技术、机械设计研究。
2016-04-05)
160820
* 中山市科技攻关项目(2014A2FC277)

