FVS-MSVM方法在机器人建模与辨识中的应用

李 军， 张观东

(兰州交通大学 自动化与电气工程学院，兰州 730070)

对于机器人轨迹跟踪控制系统设计而言，建立准确且可靠的系统模型，有利于改善控制的动静态品质[1]。但是在实际工程中，由于机器人是一个非线性和不确定性系统，难以获取其精确的数学模型。因此，实际中常采用神经网络[2-3]和模糊系统[4]等方法对机器人建模与辨识，以实现对机器人的高精度跟踪控制。近年来，SVM[5-7]、ELM(Extreme Learning Machine)[8-9]等新的计算智能方法在一般非线性系统辨识、机器人建模与控制方面也已取得成功应用。

SVM方法在算法实现中将优化问题的求解转化对偶的全局二次凸优化问题，LS-SVM作为SVM的延伸，仅涉及到求解KKT线性方程组问题，但都存在随着训练数据规模的增加而引起的核矩阵运算困难等问题。另外一类如KPCA[10]等方法也存在着求解过程中内存消耗较大的类似问题。文献[11]提出一种FVS方法，它将输入数据通过核技术映射至高维特征空间，从特征空间上的训练数据集中选取相关的数据向量构成特征空间的一个基底，称之为特征子空间，再将训练数据投影至子空间，应用经典的线性判别或线性回归方法建立分类或回归模型，在基准分类及回归问题上取得了很好的效果。文献[12]将FVS与支持向量数据描述(SVDD)方法结合，成功应用于TE化工过程监控中。

另一方面，考虑到标准SVM方法不能处理多输出的问题，通常仅考虑对系统的每一输出单独应用单输出的SVM方法进行辨识或控制，但这忽视了系统多输出之间的耦合性，具有一定的应用局限性。文献[13]给出了一种多输出SVM方法，并成功应用于超光谱图像的遥感生物物理学参数估计中。多输出SVM方法保持了在ε不敏感损失函数下具有紧凑与稀疏解的优点。鉴于FVS与MSVM方法的各自优点，针对复杂的机器人系统非线性辨识问题，本文提出一种FVS-MSVM方法，通过应用于液压驱动机器人油压辨识、6 自由度(Degree Of Freedom，DOF)工业机器人PUMA 560逆向运动学辨识及7 DOFSARCOS仿生机器人逆向动力学辨识的实例中，还与现有的其它辨识方法及相关文献的结果在同等条件进行比较，以验证本文方法的有效性。

1 FVS方法

FVS方法在高维特征空间选取相关的数据，即特征向量，形成特征子空间的基底，从而抓住了特征空间中全部数据向量的几何结构特性。

给定数据{x∈Rn,yi∈RQ}，i=1,2,…,M，变换至特征空间F上， 即有x→φ(x)∈RN。 定义X={φ(x1)φ(x2)…φ(xM)}， 核函数k(xi,xj)=φ(xi)Tφ(xj)， 简记为ki,j， 则有核矩阵K=XTX， 其元素为ki,j。

对核矩阵可进行中心化处理， 特征空间的数据φ(xi)简记为φi， 则有数据均值

(1)

式中：bj=1/M。 因此，核矩阵中心化后为

(2)

式中： 单位矩阵IM∈RM×M， 矩阵BM的列向量为b=(b1,…,bM)T。

(3)

式中：ΦS={φS1,…,φSL}， 权系数向量ai∈RM×L。

(4)

(5)

为了使δi取得最小值， 则需将式(5)对ai求偏导， 可得

(6)

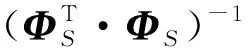
(7)

因此，

(8)

针对FV的内积， 可定义核矩阵KSS及核函数向量kSi如下：

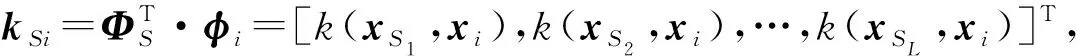
式(8)可变形为

(9)

针对F中所有数据xi(i=1,2,…,M;xi∈Rn)为找到满足最小化式(9)的特征子空间S， 则有

(10)

由式(10)针对给定的集合S， 可分别定义局部适应度(local fitness)JSi与全局适应度(global fitness)JS，即有

(11)

(12)

由式(11)与式(12)可知，求解式(10)可转化为

(13)

注意，一旦全体φ(xi)∈S， 式(12)的最大值为1， 式(4)的δi值为0。 因此， 随着L的增加， 仅需使用(M-L)个余下的数据计算选取式(13)。

FVS方法是一种前向顺序选择FV的迭代方法。在第一次迭代时，选择具有最大全局适应度的数据作为FV， 即使得JS为最大。 与此同时，基于局部适应度JSi选择下一个候选基向量， 对于目前的基向量而言， 该JSi的值最小， 即在几何结构上，候选基向量与当前基向量之间夹角θi最大。 除第一次迭代之外，算法实现过程中用最小的JSi选择新的基向量， 也就是特征向量(FV)并计算全局适应度。JS是单调递增的， 因为新的FVs与前一次的FVs一样，可以重构出所有的数据。随着迭代过程的进行，所选择的FVs近似于正交，最终使得数值解满足要求且稳定。

另外，在每次迭代时，均需计算新的全局适应度，与此同时，还需再次用局部适应度寻找下一个最好的候选FV。为避免计算矩阵的逆，从降低计算复杂度方面考虑，可采用分块求逆法，仅当KSS不再是数值可逆时，终止该操作。

为完成算法的递推实现过程，在第L次迭代过程中，也即选择第L个FV时， 需由式(11)计算第个局部适应度， 式(12)分子项可表示为

(14)

式中：S(L)={S1,…,SL}表示第L次迭代时的基向量集合， 因此它包含了L个已选择的FVs。为递推计算的方便，定义：

(15)

则式(14)等价于

(16)

且有

(17)

式中：kS(L)i∈RL是第(L-1)次迭代时向量kS(L-1)i的增广， 即第L次迭代时增加了所选择的FV=SL， 这也表明

S(L)=S(L-1)∪{SL}

(18)

考虑到核矩阵KS(L)S(L)的分块求逆， 由式(16)及式(17)，式(15)变换为

(19)

式中：cL=ψS(L-1)SL-kSLSL为标量，hS(L)i∈RL。

算法的停止条件是JS达到设定值，或者FV达到预置数目。FVS方法的算法具体实现步骤如下：

步骤1设置迭代终止参数： 全局适应度JS的上界maxFitness， 及应选择FVs的数目N并且置迭代次数L=0及特征子空间S为空， 适应度变量fitness=0，由式(2)对核矩阵K中心化。

步骤4判断是否达到终止条件，若未达到则重复执行步骤3，否则，选取FV的过程结束，S={S1,…,SL}。

第一次迭代时，涉及到全部数据的核矩阵计算，所以计算复杂度为O(M2)，L>1的迭代过程由于使用递推计算，其计算复杂度为O(ML2)。

FVS方法中的核函数可以选取常见的高斯核函数，其形式为

k(xi,xj)=exp{-‖xi-xj‖2/(2δ2)}

(20)

2 FVS-MSVM方法

特征子空间S被选定后， 所有数据可投影至该特征子空间中。考虑以点积形式计算xi在S中的投影zi时，zi应为

(21)

考虑以正交投影形式计算xi在S中的投影zi时，zi应为

(22)

考虑到SVM方法在建模方面的优势，将FVS方法看作数据预处理，可以与SVM方法组合，形成一类新的建模方法。

所有训练数据点xi均由式(21)经点积投影至特征子空间，变换后数据集为(zi,yi)。 由于标准的单输出ε-SVM无法处理多输出问题，核岭回归(KRR)可处理多输出问题但失去了解的稀疏性。在单输出ε-SVM的基础上， 可给出多输出ε-SVM方法， 此时需考虑每一单独输出之间的耦合关系，可能会获得更精确的结果。设MSVM的权值矩阵W=[w1,…,wQ]， 偏置b=[b1,…,bQ]， 需对如下所示的目标函数进行最小化优化求解，即有

(23)

受KRR方法的启发， 可使用L2范数的ε不敏感损失函数，各维输出能在唯一的限制条件下产生单一的支持向量。因此，式(23)中的ε-损失函数L(u)为

(24)

为了不增加计算复杂度，式(23)的优化求解可通过迭代重加权最小二乘(IRWLS)[13]算法进行， 直至找到最优解。 令k为迭代次数，Wk，bk为当前解。 首先，对式(23)中的L(u)进行一阶泰勒展开， 式(23)的近似表达为

(25)

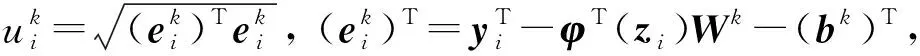
此时，可对式(24)进行二次逼近，即

(26)

式(26)表明它是一个加权最小二乘问题，权值与考虑yi各个输出的先验知识的上一次求解有关。为优化式(23)，可通过优化式(25)求得其下降方向，然后用基于线性搜索算法计算下一步的解。因此， IRWLS算法的具体实现步骤如下：

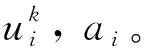
步骤2由式(25)的解求得WS，bS， 定义式(23)的下降方向为

(27)

步骤3计算下一步的解，即

式中：ηk为步长，它的计算可应用文献[14]提出的反向跟踪算法。

求解WS，bS时，由于各维输出之间无耦合，故可令式(26)的梯度方程为零，即

(28)

式(28)可表示为线性系统方程，即

(29)

式中：yj=[y1j,…,yMj]， (Da)ij=[aiδ(i-j)],δ为脉冲函数，Ψ=[φ(z1),…,φ(zM)]T,a=[a1,…,aM]T，I为所有元素为1的列向量。

(30)

式中： (K1)ij=k1(zi,zj)。 对于单输出的ε-SVM， 则有

(31)

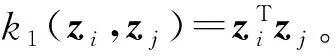
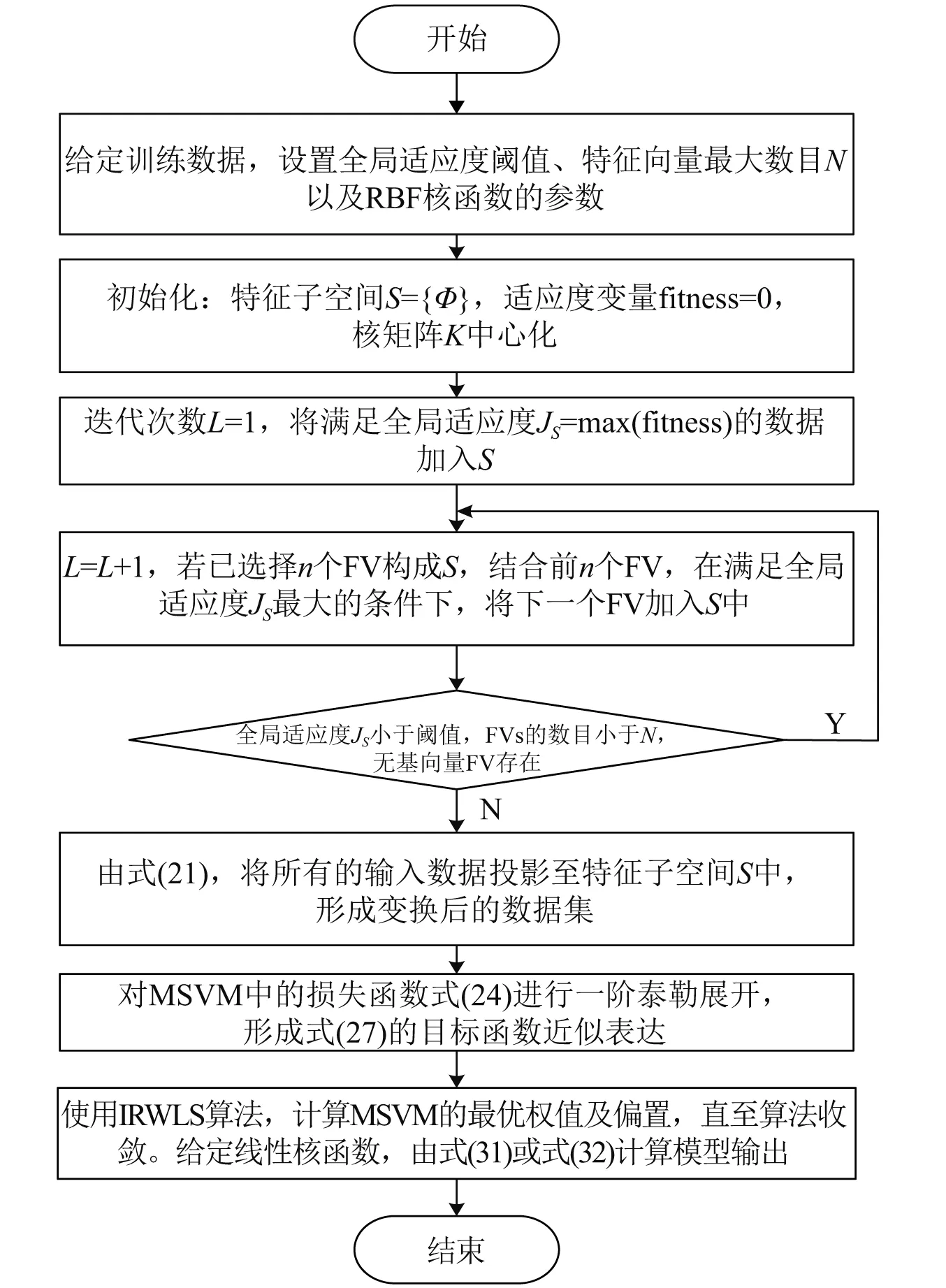
图1 FVS-MSVM方法的流程图Fig.1 Flowchart of FVS-MSVM method

3 FVS-MSVM在SISO机器人辨识中的应用

液压驱动机器人(hydraulic actuator)由液压驱动器中油压实施控制，即通过液压驱动器阀门开度位置u控制油压y的大小，阀门燃油进入驱动器给机器人臂供能。因此，通过控制阀门的开度u，可控制油压y的大小，进而可控制机器人臂的所处位置。数据来源于文献[16]，实际采集过程中，阀门的开度位置u为输入，油压y为系统输出，共获取1 024组数据。图2给出了阀门开度位置u与油压y的实际测量值波形，由图可知，当阀门开度位置u呈现阶跃变化时，由于机械共振现象，油压测量值显现出震荡行为。

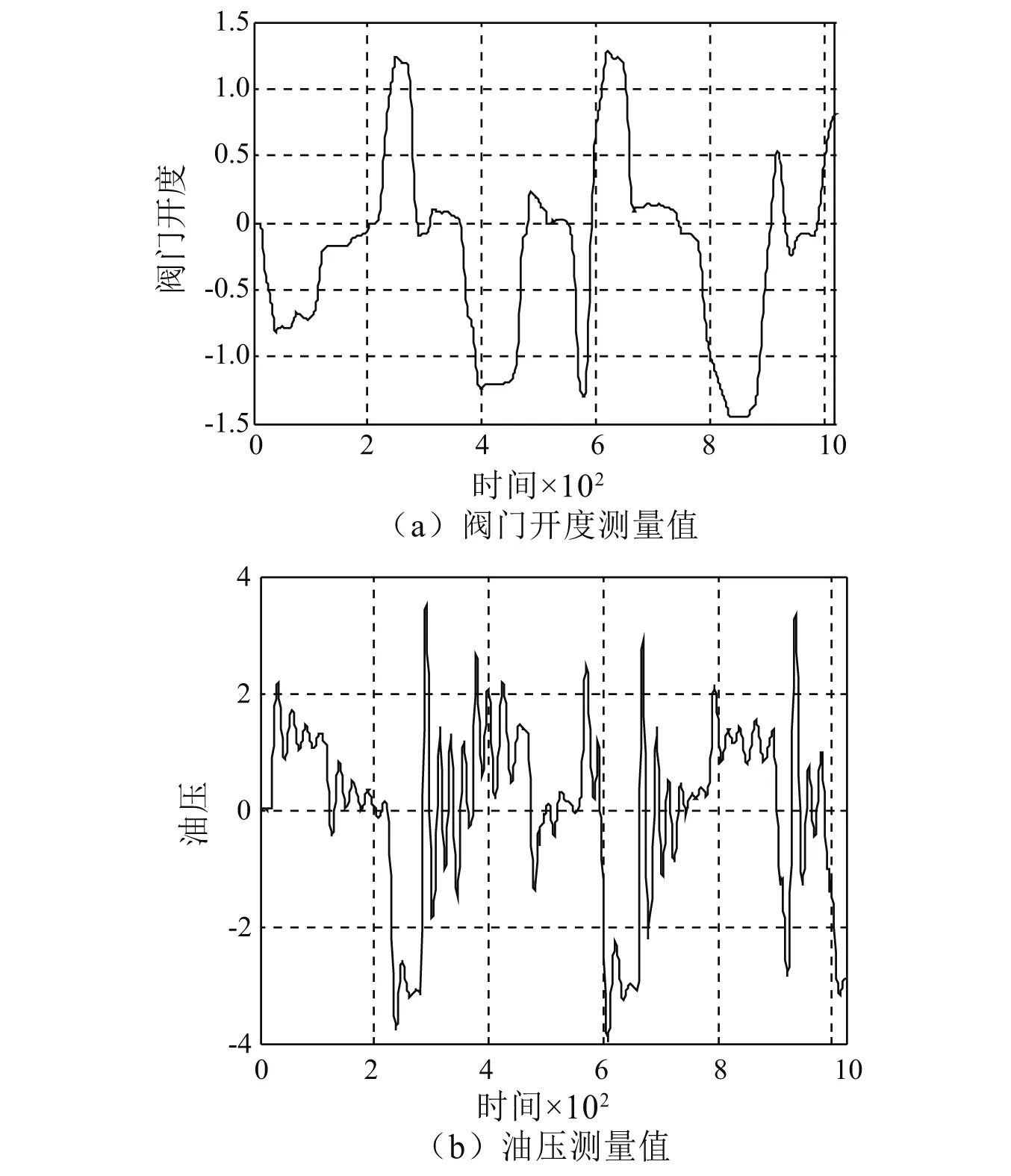
图2 阀门开度与油压测量值的时间序列Fig.2 Measured values of opening and pressure

对于液压驱动机器人油压系统，其辨识模型可表示为

(32)

式中：ny,nu分别为模型输出及输入的阶次。实验中前一半为训练数据，余下部分为测试数据。取辨识模型的ny=3,nu=2。 FV的最大数目N=50， 全局适应度阈值JS=0.989， 式(20)中的δ=2。

图3(a)给出了基于FVS-MSVM液压驱动机器人油压在线辨识结果，图中黑色实线为期望输出，黑色虚线为FVS-MSVM实际输出，图3(b)给出了全局适应度JS与FV数目之间的变化关系曲线，随着FV数目的增加， 当JS=0.989时， FV的数目为34。由图3可见，所提方法可呈现出较好的辨识效果。

表1进一步给出了FVS-MSVM方法与其它不同方法的训练时间对比，及在测试数据集的辨识结果数值比较。其中，基于文献[17]的AR-SOM神经网络方法， 选取13×14的二维网络结构， 邻域宽度σ0=5.65,σT=0.01； 在ELM方法中，隐含层节点考虑可加性节点，节点数目为30，隐含层节点参数在[-1,1]之间随机确定；KPCA-SVM方法中，取非线性主元为8。由表1可知， FVS-MSVM方法在训练时间及辨识精度上均具有明显的优势。

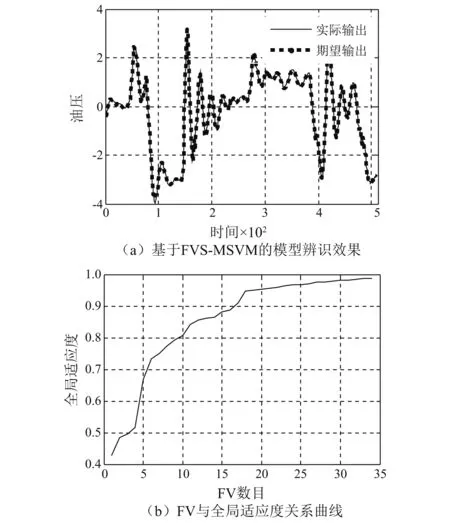
图3 油压输出的辨识结果Fig.3 Identification result of oil pressure output

本文方法还与文献[16]采用小波神经网络方法的结果进行了对比。其中，文献[16]的RMSE=0.467， 本文方法的结果明显占优。

表1 不同方法的性能指标对比Tab.1 Evaluation of performance indicator for different method

4 FVS-MSVM在MIMO机器人辨识中的应用

采用FVS-LR/SVM实现了对6 DOF工业机器人PUMA 560逆向运动学系统的辨识以及7 DOF SARCOS仿生机器人动力学系统建模。实验中，针对不同的辨识对象，分别选取不同的全局适应度阈值与特征子空间基向量数量N等参数，所有辨识对象FVS均使用高斯核函数。

4.1 PUMA 560工业机器人逆向运动学

本节实验选择FVS-MSVM方法对复杂的PUMA 560工业机器人的运行轨迹进行建模与重现，PUMA 560工业机器人具有6有自由度，其所有关节均为旋转关节，文献[18]给出PUMA 560机器人D-H (Denavit-Hartenberg)参数及详细的工作过程。这个任务的目标是在执行可能包含重复状态的任一轨迹时，估计PUMA 560机器人手臂的关节角度。因此，描述末端执行器的轨迹的笛卡尔空间 (任务空间)坐标x(t)∈R3为输入变量，6个关节角θ(t)∈R6为输出变量。完成这一任务的逆向运动学辨识模型为

(33)

式中：nx、nθ分别为模型输入及输出的阶次。

实验中，使机器人末端执行器在任务空间内执行“figure-eight”路径任务，使用文献[19]的Matlab robotics toolbox，可获取数据{x(t),θ(t)}。共收集700组数据，其中600组为训练样本，余下部分为测试样本。

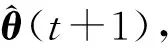
实验中，选取FV的最大数目N=300，全局适应度JS的阈值0.99， 式(20)的δ=5。 令辨识模型中的nθ=9，nx=1。 图4(a)给出了在测试数据集上对PUMA 560机器人6个关节角的模型估计值与实际值的对比结果，图中的实线为关节角的实际输出，虚线为FVS-MSVM模型的估计输出。图4(b)给出了FV 与全局适应度JS之间的关系曲线， 当JS达到阈值时， FV等于14，此时，算法停止。图4(c)则给出了末端执行器在笛卡尔空间内再生轨迹与实际的“figure-eight”轨迹对比的效果图，图中的符号“。”为末端执行器轨迹的实际输出，“*”为FVS-MSVM的模型估计输出。由图4的结果看出，针对MIMO机器人任务空间的辨识，FVS-MSVM方法具有很好的应用效果。

表2进一步给出了FVS-MSVM方法与其它不同方法的训练时间对比，以及在测试数据集的辨识结果数值比较。其中，基于AR-SOM神经网络方法， 选取34×36的二维网络结构，邻域宽度σ0=3.5,σT=0.01； 在ELM方法中，隐含层节点考虑可加性节点，节点数目为30，隐含层节点参数在[-1,1]之间随机确定；KPCA-SVM方法中，取非线性主元为12。由表2可知， FVS-MSVM方法无论在训练时间上还是在辨识精度方面均具有明显的优势。

图4 PUMA560机器人逆向运动学辨识结果Fig.4 Identification result of inverse kinematics for PUMA 560

表2 关节角6辨识结果对比Tab.2 Comparison of identification results for angular trajectories of joint 6

4.2 SARCOS机器人的逆动力学建模

本节实验考虑具有7 自由度(DOF)的SARCOS仿生机器人臂的逆动力学建模问题。数据集取自文献[20]，由48,933输入-输出数据对构成。建模任务是为规划机器人的轨迹由某个起始状态至规定状态，需要在每一时刻确定机器人的关节位置、速度及加速度，由此计算出为实现这一轨迹所需要的关节力矩，这是一个逆动力学建模问题。模型输入的第1～7维为关节位置，8～14维为关节速度，15～21维为关节加速度，模型输出则为7个关节转矩，即由21维输入映射至7维输出。由机器人在任务空间中运动约7.5 min，以50 Hz的采样频率可获得数据。实验选取第20 000～30 000个数据对，其中95%为训练数据集，余下数据为测试集。

考虑到训练数据的规模使得计算核矩阵时易导致内存溢出等问题，将数据分区，然后对每个区域内的数据子集进行特征向量选取，最终进行合并，形成一个特征子空间。将训练数据按5个分区分别选取特征向量，每个分区的FV最大数目均为N=500,JS的阈值为0.999 98， 核参数δ=2。

图5仅给出了基于FVS-MSVM 方法对关节转矩2与关节转矩4的建模效果与实际值的对比，图中实线为关节转矩的实际输出，虚线为模型的估计输出。由图5看出本文方法具有较好的建模精度。图6给出了训练时，数据分区1至分区4的FV与其全局适应度之间的关系曲线。由图6可知，当各分区的JS达到预先设置的阈值时，分区1的FV为136，分区2的FV为141，分区3的FV为197，分区4的FV为128，分区5的FV为130。因此，总的FV数目为737。

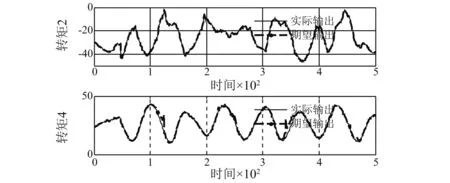
图5 基于FVS-MSVM转矩2与转矩4辨识结果Fig.5 Comparison of identification results for torque 1 and torque 4 using FVS-MSVM method

图5仅给出了基于FVS-MSVM 方法对关节转矩2与关节转矩4的建模效果与实际值的对比，图中实线为关节转矩的实际输出，虚线为模型的估计输出。由图4看出本文方法具有较好的建模精度。图6给出了训练时，数据分区1至分区4的FV与其全局适应度JS之间的关系曲线。由图6可知，当各分区的JS达到预先设置的阈值时，分区1的FV为136，分区2的FV为141，分区3的FV为197，分区4的FV为128，分区5的FV为130。因此，总的FV数目为737。

表3进一步给出在测试数据集上，针对关节转矩1，本文方法与其他方法的建模结果对比。其中， AR-SOM神经网络方法，选取16×22的二维网络结构， 邻域宽度σ0=80,σT=0.001； ELM方法的隐含层节点考虑可加性节点，节点数目为40，隐含层节点参数在[-1,1]之间随机确定；KPCA-SVM方法中，取非线性主元为100。由表3可知， FVS-MSVM方法在训练时间及建模精度上均具有较明显的优势。

图6 FV与全局适应度关系曲线Fig.6 FV and global fitness relationship curve

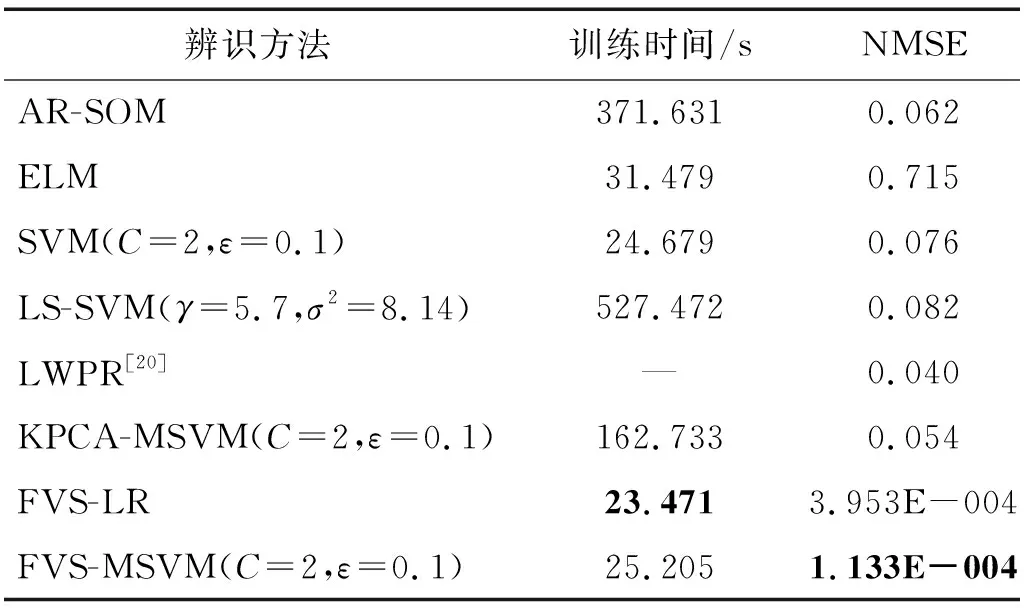
表3 转矩1辨识结果对比Tab.3 Comparison of identification results using different method for torque1

5 结 论

针对复杂的机器人非线性建模与辨识问题，鉴于FVS与MSVM方法的各自优点，本文提出一种FVS-MSVM方法。FVS方法具有对数据包含的内在特征进行预提取的优点，对映射至高维特征空间的数据，考虑几何结构，由核技术提取相关的数据向量，张成高维特征空间的一个基底，所选择的特征向量形成一个特征子空间。在此基础上，可将训练数据投影至该特征子空间上，基于MSVM方法建立辨识模型，MSVM方法保持了基于标准ε不敏感损失函数的单输出SVM方法所具有的紧凑与稀疏解特性。

为验证FVS-MSVM方法的有效性，应用于液压驱动机器人的油压辨识、PUMA 560工业机器人逆向运动学辨识、SARCOS仿生机器人逆向动力学建模中。在同等条件下与AR-SOM、SVM、LS-SVM、ELM、KPCA-SVM及FVS-LR方法进行了比较。结果表明，所提方法具有很好的建模与辨识精度，模型的泛化性能好。进一步的研究是探讨不同核函数对建模精度的影响，以及延伸应用非线性系统控制中。