涂敷硬涂层的整体叶盘振动特性与阻尼解析分析
高 峰, 孙 伟
(1. 东北大学 机械工程与自动化学院,沈阳 110819;2. 东北大学 航空动力装备振动及控制教育部重点实验室,沈阳 110819)
整体叶盘能够有效提高推重比和气动效率,刚性好,平衡精度高[1],已成为第四、五代战机的必选结构。但是,整体叶盘在真实工况下对失谐具有更高的灵敏度,会促使局部振动超标,严重威胁发动机的可靠性与飞行安全[2]。相关统计表明,叶片的振动疲劳失效而引发的故障要占发动机振动故障的70%以上[3]。因此,叶盘结构的有效减振具有非常重要的实际价值和意义。
对于传统的榫接叶盘,一般利用摩擦阻尼器的摩擦耗能来降低结构的振动应力。Laxalde等[4]利用附加摩擦环实现了对轮盘的振动控制,单颖春等[5]利用凸肩干摩擦实现了对叶片的振动控制,陈俊杰等[6]利用叶冠干摩擦实现了对传统叶盘的振动控制。而对于一体化结构的整体叶盘,干摩擦阻尼减振实施起来比较困难。表面涂层技术主要是通过对结构表面进行性能优化,提高材料表面性能,实现结构性能的大幅提高。由金属基、陶瓷基或两者的混合制成的硬涂层具有较高硬度同时又具有耐高温、耐摩擦、耐腐蚀的能力,被广泛应用在汽车、航天等领域。近年来发现,硬涂层颗粒之间的内部摩擦还能够增加系统阻尼,降低构件的振动应力[7-10],而且刚度可设计[11-12],形成硬涂层振动控制研究的新方向,其振动特性分析已成为复合材料领域中非常重要的研究课题。Giulian等[13]研究了在PWAl484超耐热合金上沉积镍衣铝粉扩散强化的Pt薄膜在高温下的阻尼性能,结果表明,镍衣铝粉扩散强化的Pt薄膜提高了超耐热合金的在所有温度下的阻尼,在高温时效果尤其明显;Yen等[14]利用磁力涂层来提高涡轮机叶片的阻尼特性,结果显示磁力涂层对能量消耗的影响与应力紧密相关,而与振动频率无关。因此,本文通过对叶片涂敷硬涂层来提高整体叶盘的结构阻尼,从而实现整体叶盘的振动控制。
对于这类涂层复合结构,由于硬涂层的材料损耗因子虽大于但并非远远大于基体的材料损耗因子,所以在对其进行动力学分析时必须同时考虑基体与硬涂层的能量耗散。由于传统的实模量理论无法满足这一要求,所以国内外众多学者广泛使用复模量理论进行研究。例如,Kung等[15]求解了黏弹性复合叶片的谐响应,Zheng 等[16]推导了约束阻尼梁的振动方程并对其进行了振动分析及阻尼性能分析,齐飞等[17]获得了黏弹性自由阻尼薄板的动力学方程并求解了固有特性。此外,对于边界条件与连续条件复杂的结构,里兹法被广泛用来求解结构振动特性的近似方法。例如,Omprakash等[18]利用循环对称性与里兹法求解了谐调叶盘的固有频率,Yang等[19]创建了单转子系统模型,并分析了轴的扭转模态、叶片的弯曲模态与轴-叶盘的耦合振动影响, Lee等[20]创建了预设叶片弯曲的轴-叶片-刚性轮盘系统模型,研究了扭转模态与轴-叶盘的耦合振动影响。
本文展开对涂敷硬涂层的整体叶盘固有特性的分析。首先,利用Oberst梁理论,推导了涂敷硬涂层的叶片的等效材料参数表达式。其次,利用复模量理论与里兹法分别求解了复合结构的能量方程与特征方程,求解了复合结构的固有特性。最后,选取了叶片单面涂敷NiCoCrAlY+YSZ硬涂层的具有18个扇区的整体叶盘为研究对象,求解了复合结构在理论上的固有特性,并与其实验数据进行了对应比较和讨论,从而验证了本文解析分析的有效性。此外,通过对整体叶盘在涂敷硬涂层前、后的固有特性的比较和讨论,探究了硬涂层对整体叶盘固有特性的具体影响,尤其是硬涂层涂敷厚度与面积对整体叶盘阻尼性能的影响规律。结果表明,硬涂层不会对整体叶盘的固有频率造成较大变化,但是对其损耗因子有着非常明显的影响,说明硬涂层可以显著增强整体叶盘的阻尼能力。此外发现,如果涂层厚度或面积增加时,复合结构的阻尼性能也随之逐步增强,但是增强的幅度并不是均匀变化的,而是有一定的变化规律。
1 复合结构的分析模型
图1所示为叶片涂敷硬涂层的整体叶盘复合结构连续参数模型,即板(轮盘)梁(叶片)模型,并且根据结构特点创建了合理的分析坐标系:在轮盘结构建立了以Qd为中心的圆柱坐标系(r,θ,z),在涂敷硬涂层的叶片结构建立了以Ob为中心的笛卡尔坐标系(xp,yp,zp)。Ω表示复合结构的转速;φ表示涂敷硬涂层的叶片结构的安装角;Ri、Ro与h分别表示轮盘结构的内径、外径与厚度;涂敷硬涂层的叶片结构沿着轮盘外缘均匀间隔分布,扇区弧度为2π/P,其中P表示整体叶盘的扇区数目,Lb、Wb与h0分别表示它的长度、宽度与厚度;wd与wbp分别表示轮盘结构与涂敷硬涂层的叶片结构在圆柱坐标系z方向和笛卡尔坐标系zp方向上的位移。
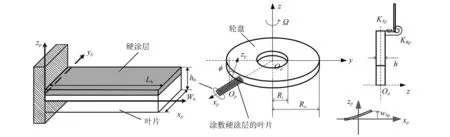
图1 涂敷硬涂层的整体叶盘示意图Fig.1 Sketch map of the hard-coating blisk
此外,为了充分考虑轮盘结构与涂敷硬涂层的叶片结构之间的耦合影响,在两者之间引入具有平移刚度KTp与旋转刚度KRp假想气动弹簧。
2 复合结构的理论分析
图2所示为涂敷硬涂层的叶片结构的简化梁模型。其中,hb与hc分别表示叶片(梁)的厚度与硬涂层的厚度,而且满足条件hb+hc=h0。
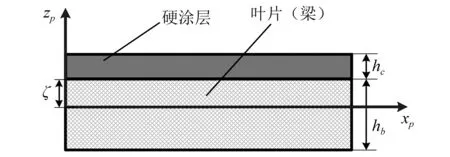
图2 复合叶片的简化梁模型Fig. 2 Oberst beam model of the composite blades
2.1 涂敷硬涂层的叶片材料参数等效
对于这类涂层复合结构,直接进行分析通常造成计算的复杂性,为此,一般对其进行参数等效化处理,即可以解决模型计算量过大的难题[21]。在同时考虑基体与硬涂层材料损耗因子的情况下,根据复模量理论可以得到叶片结构与硬涂层的复模量表达式分别为
(1)
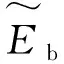
当仅考虑涂敷硬涂层的叶片发生弯曲变形的情况下,复合叶片的平衡方程[22]可以表示为
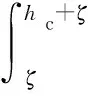
(2)
则可以得到复合叶片接触面与中性面的距离ζ为
(3)
(4)
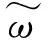
(5)
将式(2)代入式(5),整理可得
(6)
(7)
式中:Ecb与ηcb分别表示复合叶片的等效杨氏模量与等效损耗因子,且能具体表示为
(8)
此外,假设ρbd和ρhc分别表示未涂敷硬涂层的整体叶盘结构的密度与硬涂层的密度,则可得到涂敷硬涂层的叶片结构的等效密度ρb,即
(9)
2.2 复合结构的能量方程
假设▽2表示拉普拉斯算子,v表示未涂敷硬涂层的整体叶盘结构的泊松比,则涂敷硬涂层的叶片结构的应变能Sb与轮盘结构的应变能Sd可以分别表示为
(10)
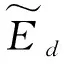
(11)
式中:ρd表示轮盘结构的密度;Ab表示单个涂敷硬涂层的叶片结构的体积。
当复合结构以固定转速Ω旋转时,耦合假想弹簧的势能Us可以表示为
(12)
涂敷硬涂层的叶片结构的势能Ub可以表示为
(13)
轮盘结构的势能Ud可以表示为
(14)
其中,u表示轮盘结构的径向位移,且有
(15)
2.3 复合结构的固有特性
当复合结构自由振动时,涂敷硬涂层的叶片结构的位移wbp与轮盘结构的位移wd可以分别表示为
(16)
而且满足
(17)
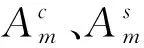
将能量表达式(10)~(14)代入拉格朗日方程,可以得到复合结构的总势能Π,即
Π=Tb+Td-(Sb+Sd+Us+Ub+Ud)
(18)
根据最小势能原理,求解式(18)的最小值Πmin可以得到复合结构的特征方程,即
(19)
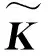
随后,根据复特征值的定义[23],可得到复合结构在第j阶的固有频率fj和模态损耗因子ηj,即
(20)
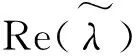
(21)
进一步,可得涂敷硬涂层的整体叶盘频响函数为
(22)
3 研究实例
3.1 基本参数
图3所示为涂敷硬涂层的整体叶盘连续参数模型,具有18个扇区,硬涂层涂敷在整体叶盘叶片的单侧,涂敷厚度为0.3 mm,涂敷面积为100%。
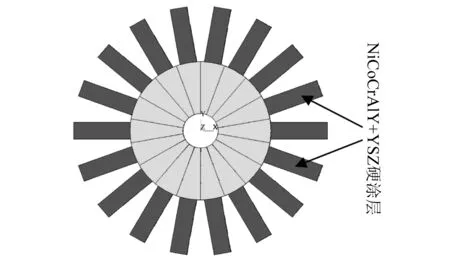
图3 涂敷硬涂层的整体叶盘连续参数模型Fig.3 CPM of the hard-coating blisk
图4为涂敷硬涂层的整体叶盘实验流程及关键设备,主要包括模态力锤,固定夹具, B&K-4517轻质加速度传感器,信号采集的端控制器与移动工作站及专业测试软件LMS Test.lab。实验基本测试流程如下:首先由模态力锤按顺序依次锤击126个(18×7)测试点来激发涂敷硬涂层的整体叶盘,轻质B&K-4517加速度传感器固定在叶根位置,负责将测试信号传递至数据采集前端控制器,随后由移动工作站及LMS Test.lab完成数据分析工作,并由PolyMAX模块的稳态图提取固有频率与结构阻尼比。此外,为了提高数据的准确性,对每个测试点均需要连续锤击两次。
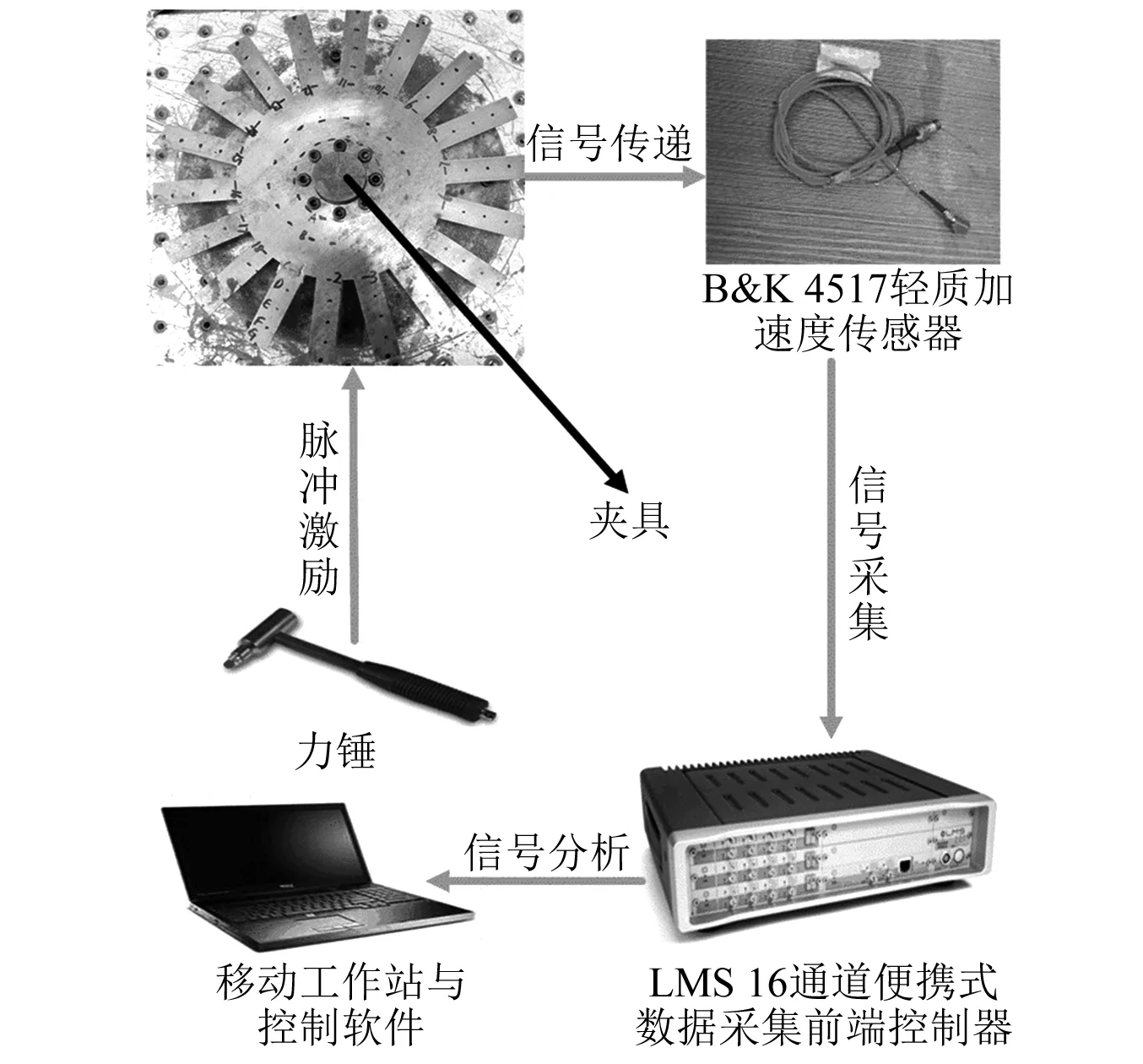
图4 模态测试实验流程Fig.4 Experimental process of modal test
表1与表2所列分别为涂敷硬涂层的整体叶盘的几何与材料参数。其中,整体叶盘的材料参数由机械设计手册获得;在室温下,通过热机械动力学分析获取NiCoCrAlY+YSZ硬涂层的杨氏模量与材料损耗因子。
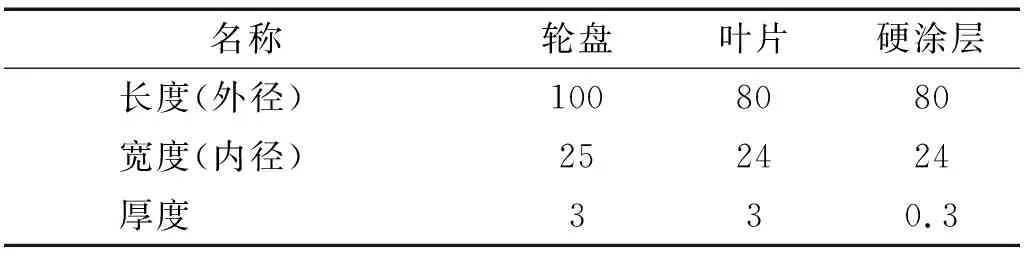
表1 涂敷硬涂层的整体叶盘几何参数Tab.1 Geometry parameters of the hard-coating blisk mm
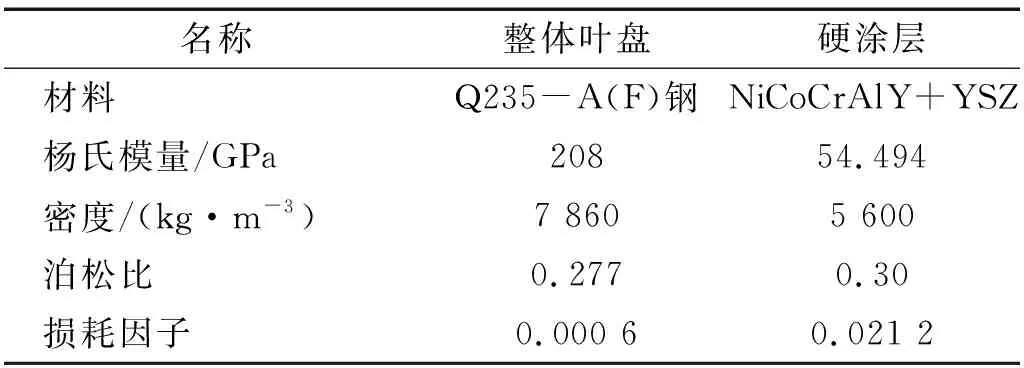
表2 涂敷硬涂层的整体叶盘材料参数Tab.2 Material parameters of the hard-coating blisk
3.2 振动特性计算及分析
图5所示是通过解析法与实验测试得到的涂敷硬涂层的整体叶盘前10阶固有频率。从内容上看,由解析分析得到的固有频率与实验测试得到的固有频率是不同的,这是因为不理想的实验环境与测试方法造成的,但是它们的数据偏差是较小的。从总体趋势上来看,两种方法得到固有频率的变化趋势是非常相似的。
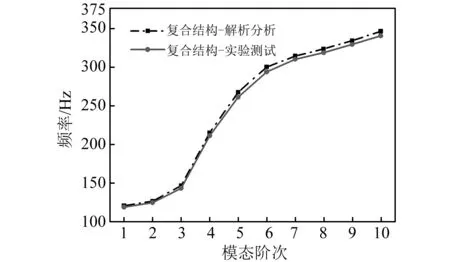
图5 由解析分析与实验测试得到的复合结构固有频率/HzFig.5 Natural frequencies of the blisk with hard coating obtained by analytical analysis and experimental test /Hz
图6所示是通过解析法与实验测试得到的节径n=3的前两阶模态振型。其中,解析分析的数据是轮盘与单个叶片的数据表示。区域A代表此处位置的振幅接近于0,区域B与区域C代表此处位置具有很大的振幅,区域D的振幅介于三者中间。可以发现,理论分析与实验测试振型的区域分布是非常相似的,而且耦合振动是整体叶盘振动的主导类型。
3.3 硬涂层对振动特性的影响
表3所列为由解析分析与实验测试得到的整体叶盘在涂敷硬涂层前、后的前10阶固有频率。从理论分析数据中可以直观的看到,整体叶盘在涂敷硬涂层后的固有频率较涂敷前的固有频率均普遍变小,但是其变化量并不大,变化率绝对值大约在1.61%~2.61%内。而且可以发现,实验测试的固有频率与解析分析的固有频率具有比较相似的变化规律,其变化率绝对值大约在1.73%~3.31%内。这就共同说明了硬涂层不会对整体叶盘的固有频率造成比较明显的影响。
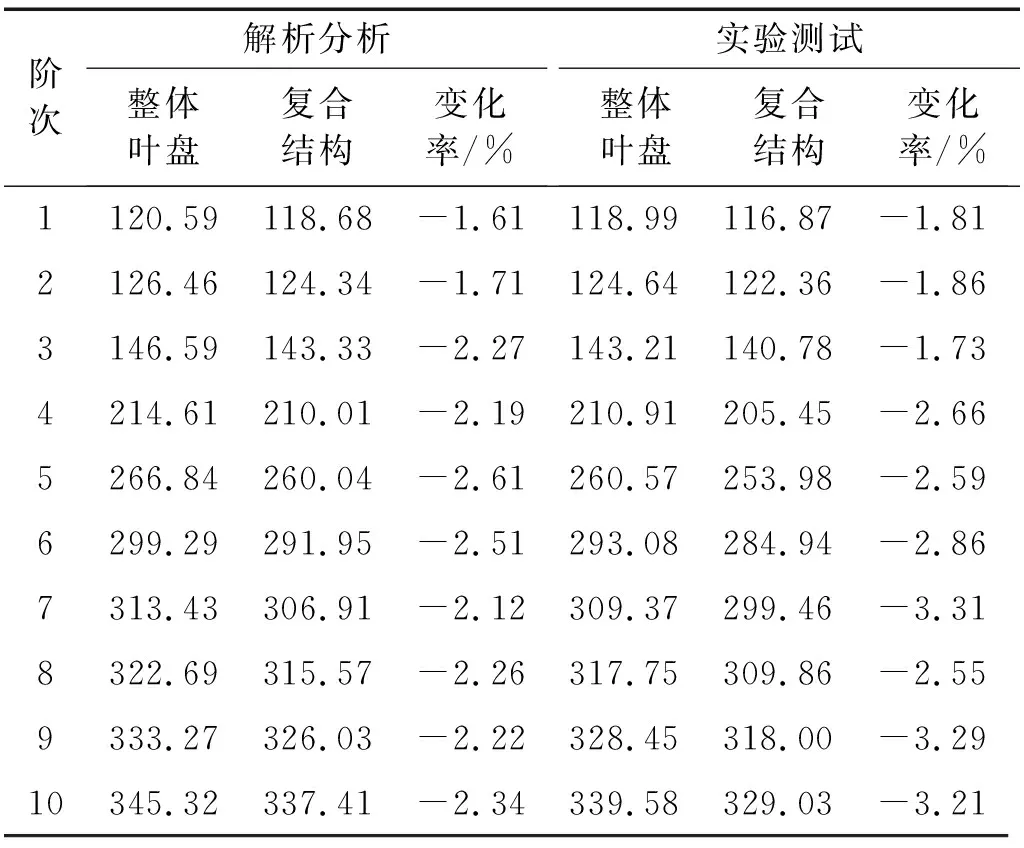
表3 涂敷硬涂层前后的整体叶盘固有频率Tab.3 Natural frequencies of the blisk with or without hard coating Hz
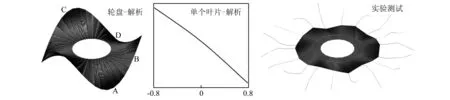
(a)第1阶模态振型
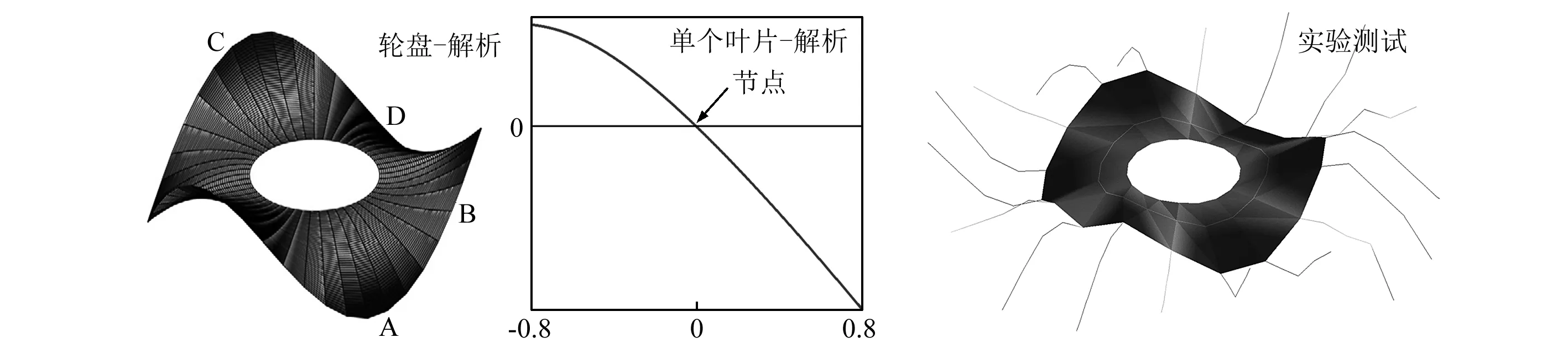
(b)第2阶模态振型图6 由解析分析与实验测试得到的涂敷硬涂层的整体叶盘模态振型Fig.6 Mode shapes of hard-coating blisk obtained by analytical analysis and experimental test
图7所示是通过解析法与实验测试得到的整体叶盘在涂敷硬涂层前、后的前10阶模态损耗因子。可以明显发现,由于实验中受到外部多种因素的干扰,所以实验测试得到的模态损耗因子都普遍大于解析分析得到的模态损耗因子,即a2>a1, b2>b1。更重要的是,无论在解析分析还是实验测试中,整体叶盘在涂敷硬涂层后的模态损耗因子较涂敷前的模态损耗因子全都显著增大了6倍左右,即b1≈6a1, b2≈6a2,这说明硬涂层能够显著增强整体叶盘的阻尼能力。
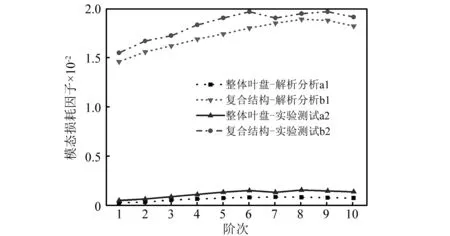
图7 由解析分析与实验测试得到的涂敷硬涂层前后的整体叶盘模态损耗因子Fig. 7 Modal loss factors of the blisk with or without hard coating obtained by analytical analysis and experimental test
图8所示为通过解析法得到的整体叶盘在涂敷硬涂层前、后的整体叶盘在节径时和0~3 000 Hz范围内的频响函数。可以清晰地看到,整体叶盘的频响函数在共振区域的幅值全都明显减小,这就说明整体叶盘在共振区域的振动响应得到显著抑制。
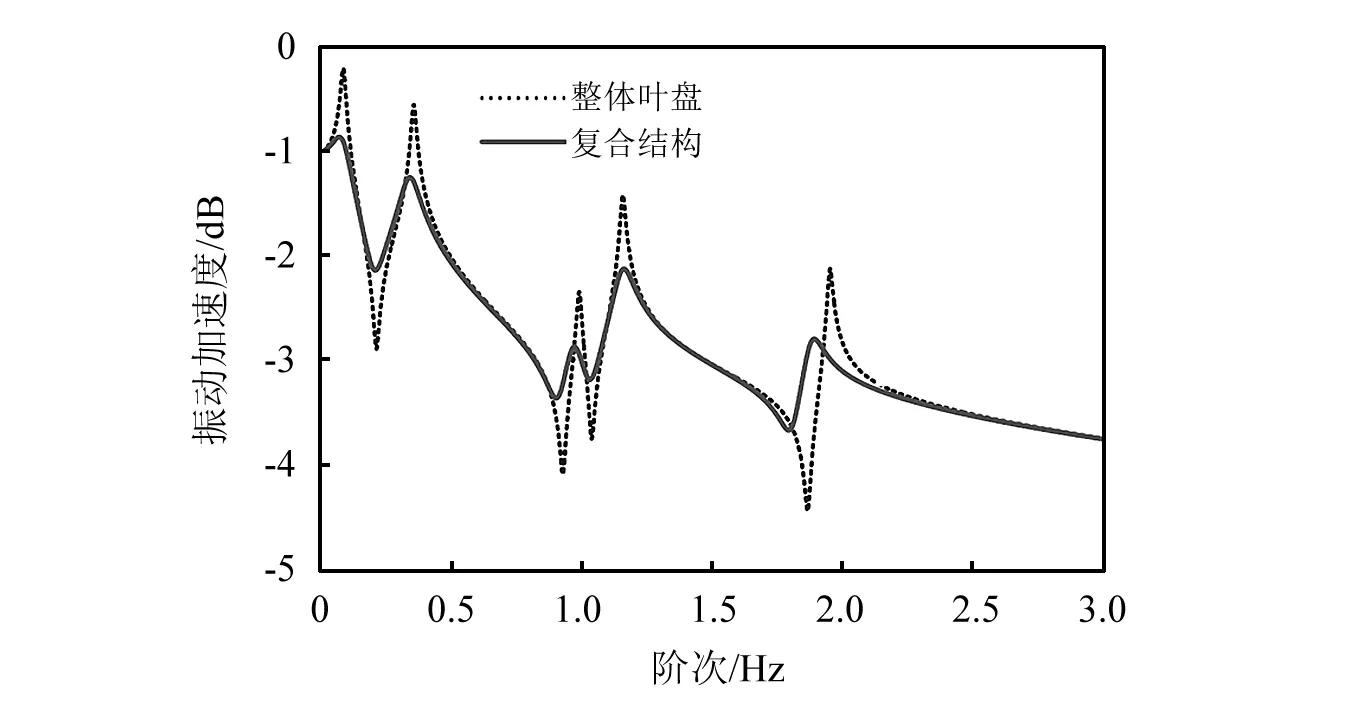
图8 由解析分析得到的涂敷硬涂层前后的整体叶盘频响函数Fig.8 Frequency response functions of the blisk with or without hard coating obtained by analytical analysis
4 涂层参数对阻尼性能的影响
在实际工程应用中,提高系统的阻尼能力是实施阻尼减振的重点,而调整整体叶盘阻尼性能灵活有效的途径就是改变硬涂层的涂敷参数。为此,本文通过解析分析分别探究了硬涂层的涂敷厚度与面积对整体叶盘模态损耗因子的具体影响规律。
图9所示为硬涂层涂敷厚度在0.1~0.5 mm的整体叶盘模态损耗因子。可以发现,随着硬涂层涂敷厚度的增加,模态损耗因子也随之增加,但是其变化梯度却不是稳定的常数,而是在逐渐减小的。当硬涂层涂敷厚度为0.3 mm,即叶片厚度/涂层厚度约等于10%时,整体叶盘的模态损耗因子变化梯度的变化率最大。
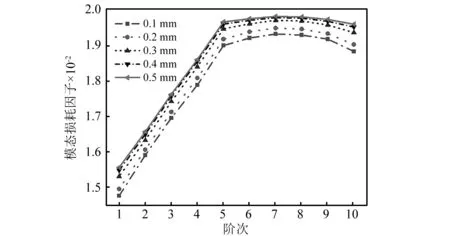
图9 不同硬涂层涂敷厚度的整体叶盘模态损耗因子Fig.9 Modal loss factors of the bliskwith different coating thickness
图10为硬涂层面积在10%~100%范围内的整体叶盘模态损耗因子(硬涂层从叶根位置开始涂敷)。可以发现,模态损耗因子会随着硬涂层面积的增加而增大,而且其变化梯度并不是常数,而是在逐渐变大,当硬涂层逼近叶尖位置时,模态损耗因子变化梯度的变化率取最大。由此知道,硬涂层应从叶尖位置开始涂敷,并逐渐向叶根拓展涂敷面积。
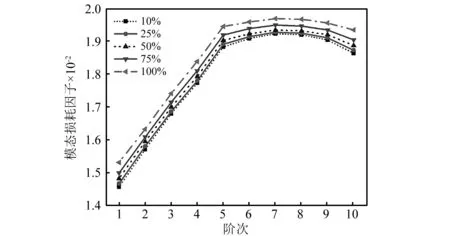
图10 不同硬涂层涂敷面积的整体叶盘模态损耗因子Fig.10 Modal loss factors of the blisk with different coating area
5 结 论
(1)利用对叶片涂敷硬涂层的方法来实现整体叶盘的振动控制,创建了复合结构的连续参数模型,并利用Oberst梁、复模量理论和Ritz法推导了涂敷硬涂层的整体叶盘的特征方程与频响函数。
(2)NiCoCrAlY+YSZ硬涂层会引起整体叶盘固有频的率略微变化,变化率大约3%,但会使整体叶盘的模态损耗因子提高了至少6倍,即有效增强整体叶盘的阻尼性能,实现叶盘结构振动的有效控制。
(3)研究了涂层厚度与面积对整体叶盘固有特性的影响。结果发现,当硬涂层的涂敷厚度与叶片厚度之比约等于10%时,模态损耗因子变化梯度的变化率有最大值,而且硬涂层应首先从叶尖开始涂敷,并根据实际需求向叶根拓展涂敷面积。

