纤维铺层角度对复合材料薄壁圆管轴向压溃吸能特性影响研究
解 江, 马骢瑶, 霍雨佳, 周 建, 牟浩蕾, 冯振宇
(中国民航大学 民航民用航空器适航审定技术重点实验室, 天津 300300)
由于具有比模量高、比强度大、质量轻及优异的吸能特性等,复合材料自20世纪80年代开始在航空航天领域得到广泛应用[1]。近年来,碳纤维增强树脂基复合材料在民用航空器中的应用比例越来越大,尤其是大量应用到机身这样的主承力结构上,如波音787和空客A350。由于复合材料结构与金属结构在失效模式和坠撞吸能机理上的显著不同,复合材料结构的使用为航空器结构适坠性设计、验证及适航审定带来了极大的技术挑战。
以民用运输类飞机为例,当发生应急着陆或坠撞时,飞机客/货舱地板下部结构能起到缓冲吸能的作用,以减少传递给机上乘员的载荷并保证客舱结构完整性,从而确保乘员的生命安全[2]。目前民用运输类飞机客/货舱地板下部主要采用重量轻、刚度高的典型薄壁结构,如果突破复合材料的失效吸能机理和设计技术,复合材料薄壁结构具备成为一种高效吸能结构的潜力,从而保证航空器的坠撞安全。2005年开始,波音公司对B787复合材料机身框段结构进行坠撞分析与设计,并从2007年起,对B787机身结构进行了3次实验:客舱地板下部结构的压缩实验;客舱地板下部结构倒置冲击实验;3 m长的机身下部结构9.14 m/s的坠撞实验。同时,FAA联合华盛顿大学等,针对B787机身下部复合材料缓冲吸能结构也开展了大量的试验方法、分析方法与吸能结构优化研究[3-6]。为B787下部结构的适坠性设计提供了重要依据。
与此同时,国内外学术界对薄壁吸能结构的吸能机理及吸能特性也进行了深入研究。Farley[7]通过压溃试验证明复合材料吸能能力是金属材料的5倍~10倍。Kindervater[8]对不同截面形状的复合材料管件吸能特性进行研究,发现方管的比吸能低于圆管,前者为后者比吸能的0.5倍~0.6倍。Farley[9]和Keal[10]研究了玻璃纤维/聚酯树脂圆管随纤维铺层角度改变对比吸能的影响,研究发现,对该材料而言,当纤维铺层角度小于65°时,比吸能与铺层角度成正比,高于65°时比吸能与铺层角度成反比。Hull等[11]研究了[±θ]铺层成型的玻璃纤维增强聚酯基圆管,发现铺层角度在35°~65°范围时,吸能能力随着角度增大而增加,在65°~90°范围时吸能能力随着角度的增大而降低。另外,国内部分研究机构及学者也针对薄壁吸能结构(圆管、方管、波纹板、复合材料增强铝管等)的吸能特性做了大量研究[12-18]。考虑到影响复合材料圆管破坏行为的因素多且复杂,需要进一步深入研究其吸能特性,进而为薄壁吸能结构设计及有限元建模提供支持。
本文针对典型航空碳纤维增强树脂基复合材料体系,考查复合材料薄壁圆管在轴向压缩载荷下的破坏吸能特性。采用LS-DYNA中的54号增强复合材料损伤模型建立了复合材料薄壁圆管有限元模型,通过对比峰值载荷及比吸能等,验证了复合材料圆管有限元模型和分析方法,基于验证的有限元方法,分析不同纤维铺层角度对复合材料薄壁圆管轴向压溃吸能特性的影响规律。
1 试验研究
本文研究的碳纤维增强的树脂基复合材料为T700/3234,其中碳纤维含量为64.3%。按照GBT1447—2005、GBT1448—2005、GBT1450.1—2005、HB7402—1996开展材料力学性能测试,获得T700/3234的主要力学性能参数,如表1所示。
复合材料薄壁圆管试验件由12层T700碳纤维增强环氧树脂层合而成,铺层角度为[±45/0/0/90/0]s,试验件高度L=100 mm,内径为D=50 mm,厚度t=1.5 mm,顶端采用45°外倒角进行削弱,从而降低初始峰值载荷便于诱导圆管发生渐进压溃,试验件如图1所示。图中θ为纤维方向与圆管轴线的夹角,本文将θ角定义为复材圆管的铺层角度。

表1 T700/3234力学性能Tab.1 Mechanical properties of T700/3234
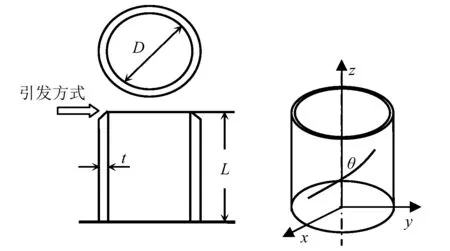
图1 试件外形几何尺寸Fig.1 Specimen dimension diagram
本文主要采用比吸能、峰值载荷、平均压溃载荷和载荷效率等指标对吸能特性进行定量分析。这些指标的具体定义如下:
(1)比吸能(Specific Energy Absorption,SEA)是指在有效破坏长度(l)内,结构单位质量(m)吸收的总能量(EA),是衡量元件吸能能力的重要参数。在压溃过程中结构所吸收的总能量可由压溃力(F)在压溃距离上的积分得到。
(1)
式中:ρ为材料密度;A为薄壁管有效横截面积。
(2)峰值载荷(Fmax)是结构被压溃破坏的门槛值,用于评价结构在外力作用下发生破坏吸能的难易程度,是载荷-位移曲线的初始峰值。
(3)平均压溃载荷(Fmean)是整个压溃过程的载荷平均值。
(2)
式中:F为压溃载荷;s为压溃位移;S为整个压溃过程的压溃总位移。
(4)载荷效率(AE)是平均压溃载荷(Fmean)与峰值载荷(Fmax)的比值。
(3)


图2 试件压溃试验前后形态以及破坏模式示意图Fig.2 Comparison of the shape before and after the test and Schematic diagram of failure mode
图2(a)和(b)给出了铺层角度为[±45/0/0/90/0]s的复合材料薄壁圆管压溃前后形态。Farley等通过试验将复合材料圆管压溃过程归纳为横向剪切、层束弯曲和局部弯曲等3种破坏模式。从图2(b)中可以看出,[±45/0/0/90/0]s复合材料薄壁圆管的压溃过程为横向剪切破坏模式,在诱发阶段,有大量短的层间裂纹和纵向层内裂纹萌发并扩展,同时分裂的层束会受到横向剪切作用,在层束基部形成弯矩,当超过材料的拉伸强度时,层束发生断裂,最终通过层束的断裂和层内裂纹的扩展来吸收能量,如图2(c)所示。对此试验件进行了两次重复试验,得到两次试验的载荷-位移曲线如图3所示,从图中可以看出,两次试验的载荷-位移曲线变化趋势吻合性较好。通过将两次重复试验的结果进行对比分析,如表2所示,可以看出,两次试验的峰值载荷偏差为9.14%,平均载荷的偏差为7.71%,比吸能的偏差为2.5%,考虑到复合材料力学性能和加工工艺的分散性[12-13],试验的重复性相对较好。

图3 复合材料薄壁圆管准静态压溃载荷-位移曲线Fig.3 Experimental load-displacement curve

表2 试件1与试件2试验数据对比Tab.2 Comparison of test data on specimen 2 and specimen 3
上述试验件的制备、力学性能测试以及圆管的压溃试验均在中航工业北京航空材料研究院完成。
2 复合材料薄壁圆管有限元模型建立与验证
2.1 有限元模型及材料参数
根据复合材料薄壁圆管试验件尺寸,采用单层壳单元有限元建模方法,建立复合材料薄壁圆管有限元模型及刚性压板模型。通过对壳单元厚度逐渐递增的方式来模拟圆管顶端45°外倒角的诱发方式,如图4所示。有限元模型采用LS-DYNA环境中的Belytschko-Tsay壳单元,54号增强复合材料损伤材料模型,T700/3234碳纤维复合材料的力学性能参数及应变失效参数如表3和表4所示。圆管上方刚性压板采用MAT 20_Rigid刚体材料,其材料参数如表5所示。有限元模型共有4 378个壳单元,4 497个节点,圆管壳单元特征长度为2 mm。

图4 复合材料薄壁圆管有限元模型Fig.4 Finite element model of the composite tube

表3 T700/3234单层板的材料参数Tab.3 Material properties of the T700/3234 lamina

表4 T700/3234单层板的失效参数Tab.4 Failure parameters of the T700/3234 lamina

表5 刚性墙材料参数表Tab.5 Material parameters of rigid wall
2.2 复合材料失效准则
在LS-DYNA的54号增强复合材料损伤材料模型中[19],材料在弹性范围内的应力-应变关系如下:
(4)
(5)
(6)
式中:σaa为纵向(纤维方向)失效应力;εaa为纵向(纤维方向)失效应变;Ea为纵向(纤维方向)弹性模量;σbb为横向(基体方向)失效应力;εbb为横向(基体方向)失效应变;Eb为横向(基体方向)弹性模量;Gab为面内剪切模量;νba为次泊松比;α是非线性剪切应力项的加权因子。当材料超出了弹性范围,MAT54材料采用Chang-Chang准则来判定铺层的失效行为,如方程(7)~(10)所示。
1)纤维拉伸模式(纤维断裂):
(7)
式中:β是在纤维拉伸模式下剪切项的加权因子,0≤β≤1.0。
当纤维断裂引起铺层失效后,Ea=Eb=Gab=νba=νab=0。
2)纤维压缩模式(纤维屈曲或扭转):
(8)
当纤维屈曲或扭转引起铺层失效后,Ea=νba=νab=0。
3)基体拉伸模式(在横向拉伸和面内剪切下的基体开裂):
(9)
当基体开裂引起铺层失效后,Ea=νba=0→Gab=0。
4)基体压缩模式(在横向压缩和面内剪切下的基体开裂):
(10)
当基体开裂引起铺层失效后,Ea=νba=νab=0→Gab=0。
在上述公式中,ef、ec、em和ed称为历史变量,分别代表纤维方向的拉伸和压缩强度以及基体方向拉伸和压缩强度的变化过程。Xt是纤维方向拉伸强度,Xc是纤维方向压缩强度,Yt是基体方向拉伸强度,Yc是基体方向压缩强度,Sc是单向层的剪切强度。剪切应力加权因子β用于定义在拉伸失效模式下剪切行为的影响。这些输入参数可以通过单向层合板试验测量得到。需要注意的是文中所有参数都是假定a方向是纤维方向,b方向是基体方向,c方向是厚度方向。
2.3 边界条件和接触定义
复合材料薄壁圆管底端固定,顶端承受刚性压板的轴向压缩载荷,以5 000 mm/s的速率匀速加载。刚性压板与圆管之间的摩擦系数设置为0.3。为防止变形过程中刚性压板和圆管之间发生穿透,在刚性压板和圆管之间设置点-面接触。
2.4 模型验证研究
图5给出了复合材料薄壁圆管的渐进失效模式图,可以看出圆管的失效行为表现为稳定的单元逐行消去,是一个渐进失效过程,但是单层壳单元模型不能模拟微观的层间裂纹及层束断裂等。从图6的压溃仿真与试验的载荷-位移曲线对比图以及表6的压溃仿真和试验的结果中可以看出,与试验结果对比,仿真结果的峰值载荷偏差为7.18%,平均载荷偏差为2.14%,比吸能偏差为-4.06%,载荷效率偏差为-4.71%。仿真与试验的载荷-位移曲线吻合度较好,从而验证了本文建模方法及复合材料薄壁圆管仿真模型的有效性。
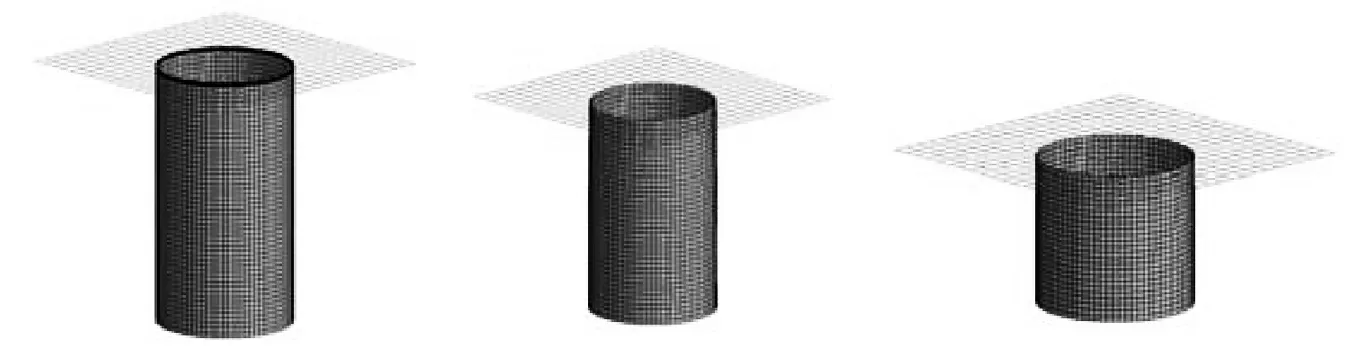
t=0 mst=4 mst=10 ms图5 复合材料圆管溃缩过程仿真Fig.5 Compression process simulation of the thin-walled composite tube
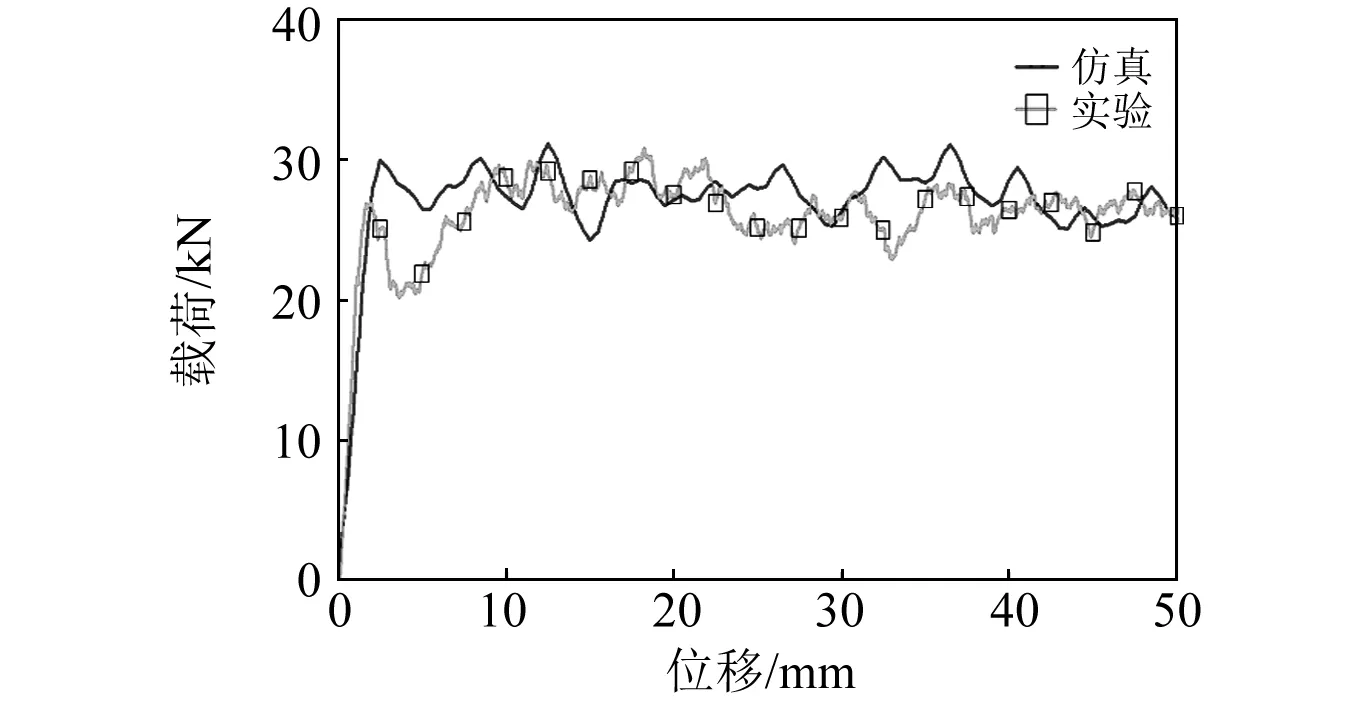
图6 复合材料圆管轴向压缩的载荷-位移曲线Fig.6 Load-displacement curve of the composite tube subject to axial compression

表6 仿真结果与试验结果对比Tab.6 Comparison between experimental results and numerical results
3 不同纤维铺层角度对圆管压溃结果影响分析
3.1 正交各向异性材料偏轴弹性特性研究
由于复合材料具有各向异性特征,实际使用过程中,单层材料的主方向与总坐标系x-y不一致,为了在统一的x-y坐标中计算材料的刚度,需要知道单层材料的圆管结构在非主方向上的弹性系数(偏轴向弹性系数)与材料主方向弹性系数之间的关系。
工程上常采用工程弹性常数来表示材料特性,在复合材料力学研究中,常采用4个沿轴常数,分别为E1,E2,υ12,G12。本文有限元模型中所使用的材料常数如表7所示。

表7 有限元模型中所使用的材料常数Tab.7 The material constants used in the finite element model
按照复合材料宏观力学基础理论,其中偏轴弹性模量为Ex,Ey,Gxy。
(11)
(12)
(13)
在此次研究中,所采用的碳纤维增强复合材料Ex,Ey,Gxy三个偏轴工程常数随着θ变化,如图7所示。

图7 材料的偏轴工程常数与θ的关系Fig.7 Relationship between off-axis engineering constants and θ
图中可见θ为0°时,Ex有极大值;θ为90°时,Ey有极大值;θ在为65°左右时,Ex趋于极小值。为了进一步说明曲线的趋势,对函数1/Ex求导:
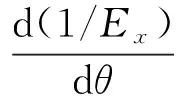
(14)
得出θ=67°。说明当铺层角度为67°时,Ex有极小值,此时复合材料薄壁圆管沿轴向的刚度最弱,最易发生破坏吸能。通过计算反映了偏轴工程常数Ex,Ey的变化特性。而Gxy关于45°对称分布。
3.2 不同纤维铺层角度圆管吸能特性仿真研究
基于验证的复合材料圆管有限元模型,考虑不同纤维铺层角度[±15°]6、[±25°]6、[±35°]6、[±45°]6、[±55°]6、[±65°]6、[±75°]6、[±90°]6,进行轴向压溃仿真,所用材料参数及加载工况同上,见表3~表5。
图8是为碳纤维/环氧圆管压溃比吸能随纤维铺层角度变化的规律,可见,当纤维铺层角度从15°增加到90°,在准静态轴向压溃下薄壁圆管的比吸能先增大,75°之后会有一定程度减小,但比吸能值仍然相对较大。产生这一变化规律的主要原因是由于纤维铺层角度不同,进而引起复合材料薄壁圆管轴向及径向刚度不同,由此在轴向加载情况下导致圆管产生了不同的破坏模式。
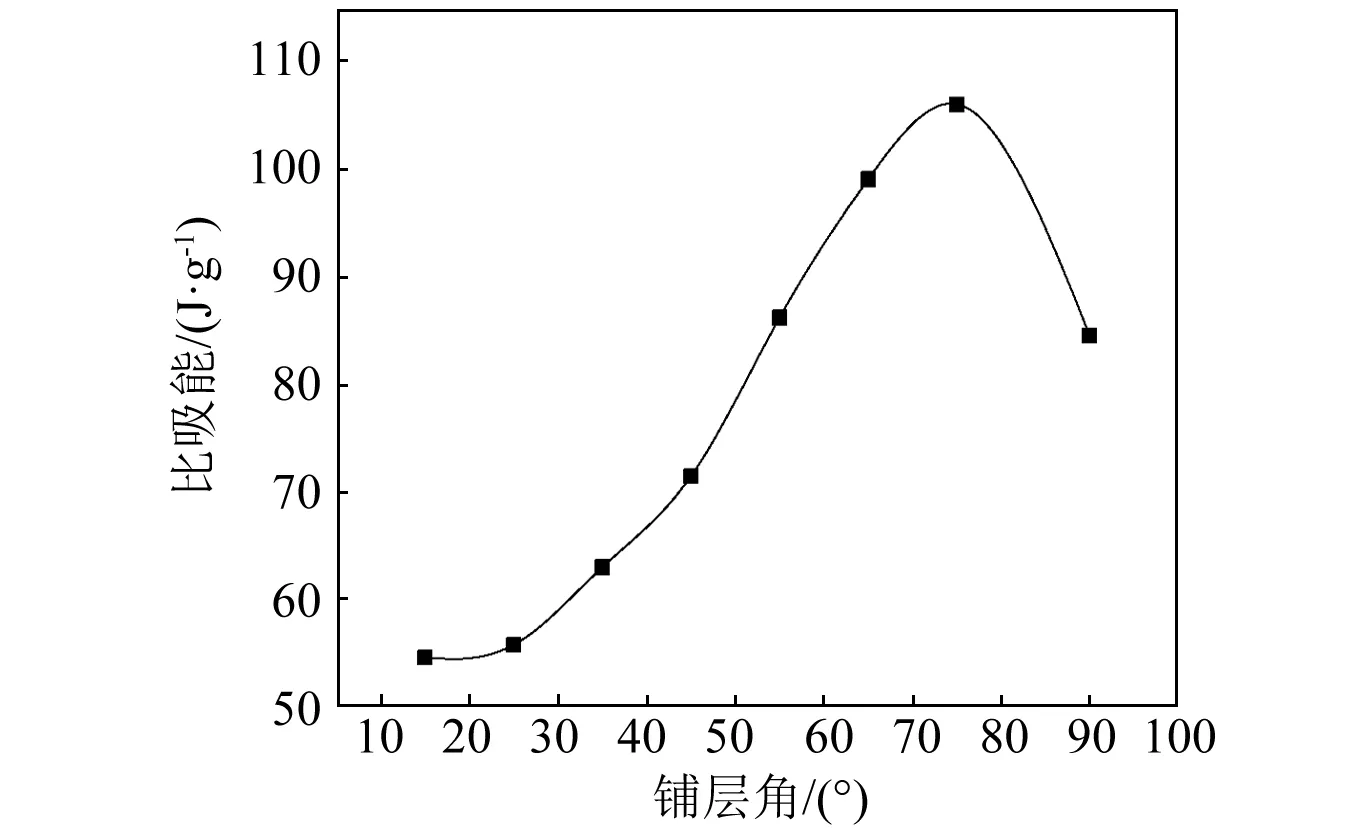
图8 不同纤维铺层角度对比吸能的影响Fig.8 Effect of different ply orientations on SAE
结合复合材料各向异性偏轴理论,当铺层角度小于45°时,纤维在圆管中主要起轴向增强作用,大量裂纹首先在强度较低的周向生成,并随着压溃进行,管壁内大量平行纤维方向的基体裂纹在单层或相邻层内沿纤维方向扩展,纤维铺设角度越靠近0°,基体越容易周向开裂使纤维沿周向开裂成分离的层束,因而比吸能值越低。
当铺层角度大于45°时,使得圆管周向刚度和强度增加,在压溃过程中,纤维与基体共同发生作用,并且随着铺层角度增加,周向纤维所占比例增加,当铺层角度为75°附近时,随着周向的开裂,导致大量纤维被拉断,断裂成细小片段,从而吸收大量能量,比吸能值增大;随后,随着铺层角度的增加,轴向刚度明显减弱,圆管在压溃过程中,容易发生失稳,导致比吸能开始减小。
另外,当结构用于缓冲吸能元件并保护乘员安全时,初始载荷峰值Fmax是能量吸收装置关系到乘员安全的重要性能指标,若初始峰值载荷过大,乘员承受的过载可能超过人体的安全极限,从而给乘员造成一定的生命安全。由于峰值载荷具有一定的分散性,所以将峰值载荷以散点图的形式表示,如图9所示,可以看出,随着纤维铺层角度的变化,初始峰值载荷在55°左右之前,基本保持在40 kN以下,45°时峰值载荷最低。之后随着角度的增大,初始峰值有了很大程度提高。这是因为,当纤维铺层角度较小时,圆管的周向刚度较弱,导致圆管容易在周向开裂,并发生破坏,从而使得压溃进程比较容易进入渐进破坏吸能阶段,所以初始峰值较低。

图9 不同纤维铺层角度对初始峰值载荷的影响Fig.9 Effect of different ply orientations on Fmax
与此同时,由于结构和空间的限制,要提高试件的耐撞性及其吸能能力,必须使其能够持续渐进压溃,那么,就需要尽量提高持续压溃平均载荷Fmean。从图10中可以明显看出,平均压溃载荷随着角度的变化趋势与图8中比吸能的变化趋势比较类似,这进一步说明,在压溃过程中,压溃平均载荷Fmean与试件的吸能能力有很大的相关性。

图10 不同纤维铺层角度对平均载荷的影响Fig.10 Effect of different ply orientations on Fmean
根据载荷效率的计算公式,如果平均压溃载荷(Fmean)与峰值载荷(Fmax)越接近,即载荷-位移曲线与坐标轴围成的区域越接近矩形,则载荷效率越接近100%,这是理论上最大的能量吸收效率。图11给出了不同纤维铺层角度对载荷效率的影响曲线,可见,±45°铺层的载荷效率最高,约为60%。另外,从图7计算偏轴刚度可发现铺层角度在45°附近时Ex、Ey交叉,此时试件在轴向与周向的刚度非常接近,在压溃过程中,达到峰值载荷之后,进入渐进破坏过程,峰值下降较少,因而载荷效率最高。
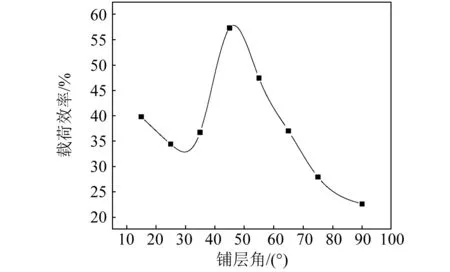
图11 不同纤维铺层角度对载荷效率的影响Fig.11 Effect of different ply orientations on LE
4 结 论
(1)通过将两次重复试验的结果进行对比分析,两次试验的峰值载荷偏差为9.14%,平均载荷的偏差为7.71%,比吸能的偏差为2.5%,表明此次试验的重复性较好。然后,采用chang-chang失效准则,建立单层壳有限元模型,将仿真计算结果与试验结果进行对比分析,仿真结果与试验的峰值载荷偏差为7.18%,平均载荷偏差为2.14%,比吸能偏差为-4.06%,载荷效率偏差为-4.71%。表明仿真与试验的载荷-位移曲线吻合度较好,从而验证了本建模方法及复合材料薄壁圆管仿真模型。
(2)基于验证的有限元模型,改变纤维铺层角度,建立[±15°]6、[±25°]6、[±35°]6、[±45°]6、[±55°]6、[±65°]6、[±75°]6、[±90°]6复合材料薄壁圆管有限元模型,结果表明:在准静态轴向压溃作用下,随着纤维铺层角度的增大,薄壁圆管比吸能先增大,在75°之后减小。纤维角度为±45°时,初始峰值载荷最低,载荷效率最高,圆管更容易进入渐进破坏吸能阶段。研究结果可为复合材料纤维铺层角度设计及复合材料薄壁结构有限元建模提供参考。

