基于响应面法的槽形梁结构噪声优化研究

刘林芽， 秦佳良， 雷晓燕, 刘全民， 宋 瑞,2

(1.华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌 330013;2.南昌工程学院 土木与建筑工程系，南昌 330029)

桥梁在列车动载作用下会向周围环境辐射噪声，其中主要以20～200 Hz频段的低频噪声为主[1]。这种低频噪声由于其波长较长，在传播过程中不易衰减，而且采用传统的声屏障还难以有效控制这种低频噪声[2]，并且对人体健康还有较大的不利影响[3-4]。而且随着我国轨道交通的不断发展，轨道交通桥梁的应用也越来越多，人们对轨道交通结构低频噪声的投诉倾向也在增多[5]。因此，对轨道交通桥梁减振降噪的研究是一个亟待解决的问题。

目前，国内外学者对桥梁减振降噪做了大量的研究，Zhang等[6-7]基于车-线-桥耦合振动理论和声学边界元理论，建立了箱梁结构噪声预测的混合有限元-边界元法，分析得出增加板厚将使箱梁结构噪声降低，且增加顶板厚度最为有效。韩江龙等[8]采用模态叠加法求解列车-轨道-桥梁动力响应，再采用模态声传递向量法求解桥梁结构噪声，分析了板厚和加肋对槽形梁结构噪声的影响。Bewes[9]对混凝土桥、钢筋混凝土桥和钢桥研究表明：增加桥梁某些结构组件的厚度，可以降低这一组件的结构噪声，但同时会增加其它组件的结构噪声。

虽然国内外学者对桥梁减振降噪做了大量的研究，但对桥梁结构声学最优截面的研究却很少，仅研究了单一板厚对结构噪声的影响。而且大多数都采用单一场点的声压级来评价桥梁降噪的效果，并不能体现出空间声场的整体降噪效果。因为同一板件对不同场点的声学贡献量是不一样的，有可能增加一个板件的厚度会降低某一个点的声压级，但却会增加另一个点的声压级。所以本文将声功率作为桥梁结构噪声优化的评价指标能避免这个问题。这是因为声功率表示的是单位时间内声源向外辐射噪声的能量多少，与距离声源的远近无关，所以在优化过程中不需要选取特定的场点。本文以轨道交通30 m简支槽形梁为研究对象，将响应面法和声学响应计算相结合，建立了以槽形梁结构辐射噪声的声功率级为目标及以槽形梁质量为约束的声学优化模型，再利用序列二次规划法进行求解，最终找出了槽形梁结构声学最优的截面尺寸，为轨道交通槽形梁的减振降噪提供了一定的依据。

1 槽形梁结构声学响应计算

1.1 轮轨激振力的获取

首先利用有限元软件ANSYS和多体动力学软件SIMPACK，建立精细化的车桥耦合空间动力学分析模型。在SIMPACK中建立车辆分析模型，车辆系统的多体动力学模型通过铰接、刚体、力元、约束以及轮轨接触模型等来形成一系列的动力学方程。一节车辆可以认为由一个车体、两个转向架、四个轮对等七个刚体构成，其中连接这些刚体的部件还可分为一、二系弹簧、横向减振器、垂向减振器，抗蛇行减振器、抗侧滚扭杆、牵引拉杆、横向止挡等。其中每个刚体考虑伸缩、横摆、浮沉、点头、侧滚、摇头6个自由度，由于左右轮上各有一个约束，所以车辆共34个自由度。

在ANSYS中建立桥梁模型，并对其进行子结构分析和模态分析处理，得到SIMPACK中有限元FEMBS可以识别的文件，再利用SIMPACK中柔性轨道模块，实现车辆模型和桥梁模型的共同求解。其中，把车辆模型和桥梁模型分别作为两个系统，它们之间通过轮轨接触点实现力、位移等的交换。然后分别轮流迭代，最终计算出轮轨之间的相互作用力，实现车桥耦合分析模型的求解。本文只考虑2节地铁A型车通过该槽形梁结构。计算速度取为80 km/h，钢轨不平顺根据ISO3095—2013标准中的不平顺限制谱生成。图1所示为车桥耦合分析模型。

图1 车桥耦合分析模型Fig.1 The model of vehicle-bridge coupling analysis

1.2 槽形梁振动响应计算的有限元法

振动是噪声的来源，所以要计算槽形梁的结构噪声必须先计算出槽形梁的振动响应。本文采用瞬态动力学分析桥梁结构的动力响应。瞬态动力学分析也称为时间历程分析，其基本运动方程为：

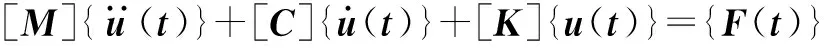
(1)

在求解槽形梁振动响应时，将列车在运行过程中产生的连续的轮轨力简化为一系列随时间移动的集中力荷载，采用节点加载的方式，将这些移动的集中力荷载加载到轨道-槽形梁有限元模型中的钢轨上，图2所示为轨道-槽形梁的有限元模型。然后对其进行瞬态动力学分析，即可计算出在列车荷载作用下槽形梁在时域内的振动响应[10]。

图2 轨道-槽形梁有限元模型Fig.2 Finite element model of track-trough girder

1.3 槽形梁结构声学响应计算的边界元法

理论上任意形状的振动结构在外部流体介质场Q中任意点P的稳态声压p(r)可由Helmholtz积分公式计算得

(2)

槽形梁表面可以被认为是具有小振幅运动的不渗透边界，满足Neumann边界条件

∂p/∂n=-iωρv

(3)

式中：n为槽形梁表面边界外法线向量；v为边界表面的法向振动速度向量；ρ为流体密度。

槽形梁结构噪声辐射在声场无穷远处不存在反射波，因此还要满足Sommerfield条件

(4)

式中：p为声压向量；r为声场中场点距源点的距离；Γ为距离源点为r处的波阵面；SΓ为波阵面面积。利用加权残值法，选用式(1)的基本解自由空间格林函数G(r,rS)，使用加权残值法可求得：

(5)

式中：R=|r-rS|；k=ω/c为波数；c为流体介质中的声速。

当式(2)中的r趋近于rS时，可得到Helmholtz表面积分方程：

(6)

其中：

C(rS)称为表面角系数。

结构的辐射声功率可通过下式求得：

(7)

式中：v*为的共轭复数。

在建立槽形梁声学分析模型时，为准确计算结构噪声，在最小波长内要有6个单元[11]，也就是最大单元的边长要小于计算频率最短波长的1/6。本文分析频率为20～200 Hz，所以最大单元的边长要满足如下表达式

(8)

槽形梁的边界元网格可以由有限元网格转化得到，所以槽形梁的有限元网格划分也应该满足式(8)。然后将列车荷载作用下轨道交通槽形梁在时域内的振动响应，通过FFT将其变换为频域内的结果，再把频域的振动响应结果作为声学计算的边界条件，导入到LMS Virtual.lab软件中，采用边界元法来计算轨道交通槽形梁结构辐射噪声的声功率。

2 响应面法介绍及原理

由于槽形梁的形状是不规则的，所以很难用显式表达式来计算槽形梁的辐射声功率。而且结构声学优化是一个反复迭代的过程，单次计算过程通常就需要花费大量的计算资源和时间，需要多次调用仿真分析软件。在优化过程中，设计变量的变化可能导致单元计算产生问题，优化迭代过程会因为单次仿真的失效而使整个优化过程无法进行。针对以上问题，本文将响应面法引入到槽形梁结构声学优化设计当中，用响应面模型代替复杂的，具有多自由度的槽形梁结构声学仿真模型。

响应面法可以采用多项式函数代替难以显式化的状态函数，通过多次迭代调整，一般都能满足实际工程精度，具有较高的效率，很有使用价值，是一个很有发展前景的计算方法，也是处理优化问题时常用的方法之一。华洪良等[12]就利用响应面法对不同结构的优化问题做了研究。响应面法是将合理的实验设计得到相关的数据采用回归方程来拟合，得到设计变量与目标函数之间的近似函数关系。利用响应面法来构造近似模型时，首先要确定近似函数的形式，然后运用统计的试验设计方法在空间内选取足够多的设计点，然后确定响应面模型多项式的次数，运用最小二乘法原理对试验设计点的结果进行拟合得到响应面模型。

结构的性能值y关于变量x的函数关系表达式f(x)往往不能用显式表达，但是只要给定了变量值就可以通过数值试验得到相应的响应值，那么就可以用拟合出来g(x)的去替代f(x)，即

y=f(x)≈g(x)

(9)

式中：g(x)表示的曲面为响应表面。

由于性能响应与变量之间函数关系未知，因此事先必须选择函数g(x)的形式。选择好的函数会使近似更精确，而且会使适合使用的设计空间域更宽广。实际中根据工程经验，通常选取二次多项式的形式，其表达式为

(10)

式中：α0为常数项待定系数；αi为一次项待定系数；αij为二次项待定系数。

为了确定待定系数，需要做m次独立试验，其中m≥k=(n+1)(n+2)/2，n为设计变量的个数。每次试验变量的取值不同，得到个样本点对应的响应值y(i)(i=0, 1, …，m-1)，由最小二乘法原理可以得出

β=(XTX)-1XTy

(11)

其中

将试验设计的变量X和对应的响应值y代入式(11)，即可求出响应面模型中的待定系数，从而得到多项式的响应面模型。

3 槽形梁声学优化的响应面模型建立

3.1 设计变量及试验设计

城市轨道交通槽形梁的翼缘板的面积很小，槽形梁也主要由底板和腹板组成，而且槽形梁的结构噪声也主要由这两部分引起的[8]，所以把槽形梁的底板厚度和腹板厚度作为响应面法的设计变量，分别用和表示。根据《地铁设计规范》(GB50157—2013)中的相关要求，底板厚度和腹板厚度的初始值及其变化范围，如表1所示。

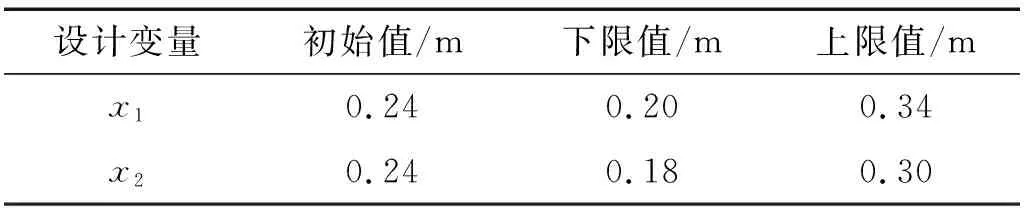
表1 槽形梁结构设计变量初始值和变化范围Tab.1 The initial value and the variation range of the design variables of trough girder

建立高精度响应面模型较大程度上取决于对设计空间的采样技术。试验设计为利用数理统计学与正交性原理，从大量试验点中选取合适的有代表性点。用正交表合理安排试验的设计方法。为保证响应面模型的精度和试验设计的次数，用中心组合设计法对设计空间采样。声功率表示的是结构向外辐射噪声的能力大小，所以把槽形梁辐射噪声频率在20～200 Hz内的总声功率级作为目标响应值，表2中列出了每次试验的变量取值及响应值。

3.2 响应面模型的建立及误差分析

根据试验设计的结果，本文采用最小二乘法对设计变量和响应值进行拟合，得到槽形梁结构辐射总声功率级关于槽形梁底板厚度和腹板厚度的二次多项式函数，其表达式为：

表2 试验仿真次数和结果Tab.2 The simulation times and the resules

(12)

为了考察得到的槽形梁结构声学优化的响应面模型能否用于后续的优化分析，需要对其进行误差分析以检验模型的拟合精度。工程中常用复相关系数R2对响应面模型进行检验，并根据统计学原理对响应面模型进行显著性检验。经过计算得，复相关系数R2=0.955>0.9，显著性检验中的p=0.031<0.05，说明本文建立的响应面模型的拟合精度高，拟合得到的响应面模型是可靠的，可以用来后续的优化设计。

4 槽形梁结构声学优化的结果

针对实际问题，为了保证优化后的槽形梁具有足够的刚度，并且考虑成本的因素，优化后的槽形梁质量应该不高于初始质量的15%，所以把槽形梁的质量变化作为约束函数，则槽形梁结构声学优化的数学模型可以表示为：

(13)

式中：m0为槽形梁结构的初始的质量；Δm为在优化过程中槽形梁结构质量的改变量；其表达式为Δm=260.78x1+211.09x2-113.25。

由式(13)可知，该优化问题属于典型的不等式约束的非线性最小优化问题，序列二次算法是求解这类优化问题最有效的算法之一，编制相应的算法程序，寻找槽形梁声学最优的截面尺寸，优化后的结果如表3中所示。槽形梁的质量从149.48 t增加到171.34 t，质量增加了14.6%，满足约束函数的条件。优化后槽形梁辐射的总声功率级为101.48 dB，而优化前总声功率级为104.92 dB，降低了3.44 dB，优化结果表明有效的降低了槽形梁在列车荷载作用下向周围环境辐射噪声的总能量。

表3 设计变量取值Tab.3 Design variable value

为了验证响应面模型优化的正确性，把槽形梁结构声学优化后的底板和腹板厚度代入槽形梁结构分析模型中，利用有限元法和边界元法计算出槽形梁辐射噪声频率在20～200 Hz内的总声功率级，将响应面模型与数值仿真的计算结果相对比，如表4所示。利用优化后的设计变量计算出的总声功率级为100.93 dB，与响应面模型的优化结果误差仅为0.54%，这也说明槽形梁结构声学优化的响应面模型具有一定的准确性。

表4 各模型计算结果Tab.4 Calculation results of each model

为分析槽形梁声学优化后的实际降噪效果，图3和图4分别给出了优化前后在整个分析频率范围内的槽形梁辐射声功率级的频谱图和面声场总体声压级的整体降噪效果图。

图3 优化前后槽形梁辐射声功率级Fig.3 Sound power level of trough girder before and after the optimization

图4 优化前后面声场总体声压级差值Fig.4 The overall sound pressure level difference of surface sound field before and after the optimization

由图3可知，在整个分析频率范围内，槽形梁辐射噪声的声功率级都有不同程度的降低，说明优化后槽形梁向外辐射噪声的能量也减少了。而且由图4可以发现，槽形梁经过声学优化后，面声场中各场点的总体声压级都有不同程度的降低，最大可降低4 dB左右。由此可知，把槽形梁辐射声功率作为评价指标是可行的，因为槽形梁优化后面声场总体声压级的降噪效果还是比较显著。

5 结 论

本文基于车桥耦合分析模型，利用有限元法和边界元法计算轨道交通30 m简支槽形梁的辐射声功率，将响应面法与辐射声功率计算相结合，建立了以槽形梁辐射结构噪声在分析频率范围内的总声功率级为目标及以槽形梁质量为约束的声学优化模型，再利用序列二次规划法进行求解，最终找出了槽形梁结构声学最优的截面尺寸。优化后槽形梁底板厚度为0.34 m，腹板厚度为0.22 m。计算结果表明，利用响应面法可以有效的对槽形梁进行声学优化，而且优化后的降噪效果还是比较显著的。