考虑风屏障效应的车桥系统三分力系数风洞试验研究
王玉晶, 郭薇薇,2, 夏 禾,2, 张 楠,2, 张 田
(1. 北京交通大学 土木建筑工程学院,北京 100044; 2. 北京市结构风工程和城市风环境重点实验室,北京 100044; 3. 大连海事大学 交通运输工程学院,辽宁 大连 116026)
随着高速铁路的迅速发展,列车在强侧风作用下的倾覆事故时有发生,风荷载作用下的行车安全问题变得愈加突出[1]。提高强风作用下列车安全性的措施主要有:优化车辆外形、通过强风监测系统控制列车运行速度和设置风屏障[2]。但是列车的降速或者停运会影响运营效率,造成一定的经济损失。而风屏障可以为列车提供一个较低风速的风环境,进而有效提高列车行车安全性。因此,对于已有车辆来说,设置风屏障更加行之有效。
近年来,很多学者通过现场实验、数值模拟与风洞试验等方法对风屏障的防风性能进行了研究。结果表明[3-5]:在路基上设置风屏障可以大大提高列车的运行安全性,但对于桥梁来说,风屏障在减小列车运行区域风速的同时增大了桥梁的迎风面积,使桥梁的风荷载加大,这是不利的。因此,人们采用孔隙式风屏障来降低桥梁风荷载。郭文华、李永乐、何旭辉等[6-9]采用风洞试验和数值模拟的方法研究了雷诺数、风攻角、风屏障参数(高度和透风率)对车桥系统气动特性的影响,并给出了风屏障高度和透风率的建议取值。
列车的气动力不仅受风屏障高度和透风率的影响,还与线路结构形式、风屏障的安装位置和行车位置有关。本文采用风洞实验的方法,对高速铁路32 m简支箱梁和16 m T梁的截面三分力系数进行了测试,对比分析了列车在不同梁型上的气动特性,并与其在平地路基上的结果进行了对比;分析了风屏障安装位置和行车位置对车桥系统气动力系数的影响;选取一种工况进行了数值模拟,并与实验结果进行对比,解释了风屏障-车-桥系统气动绕流机理;最后,对不同线路结构形式和风屏障安装位置时车辆的行车安全性进行分析。
1 试验概况
试验在北京交通大学风洞实验室进行。该风洞是一座双试验段回流大型多功能边界层风洞,风洞试验段尺寸为:3.0 m×2.0 m×15.0 m(宽×高×长)。试验风速为8~10 m/s,风场湍流度小于0.5%。
1.1 试验模型与测点布置
制作了风屏障-列车-箱梁、风屏障-列车-T梁和风屏障-列车-路基三种风洞试验模型,如图1所示。综合考虑列车和桥梁的几何尺寸、风洞高速段截面尺寸和阻塞度要求,模型(含风屏障、桥梁、列车等)的几何缩尺比为1∶32,最大阻塞比为10.5%。

图1 试验模型Fig.1 Test models
列车模型是CRH2型高速列车的中间车,忽略了转向架、轮对和门把手等细部结构,外形上与实物保持一致,以尽可能真实的模拟实际气流的绕流。箱梁模型和T梁模型的长度为2.6 m,车辆模型长度为2.4 m。箱梁和车辆模型均以钢管为骨架,外壳采用ABS板制作,以保证模型具有足够的刚度和强度,在试验中不变形且不出现明显的振动以保证测试的精度。T梁模型采用薄钢板直接冲压而成,用木质板模拟路基。风屏障模型是长度为2.6 m的圆孔式ABS板,通过三角支撑固定在线路结构表面,保证其在试验过程中不发生变形。箱梁模型和T梁模型距地面1.0 m,路基模型距地面0.5 m,车桥间距为0.02 m。

图2 测点位置及编号Fig.2 Pressure taps on vehicle surface
本试验采用压力积分法计算作用在车辆上的气动力,因此在沿列车长度方向在车体表面布置5个测压断面。为排除洞壁的气动干扰效应,将其中2个测压断面布置在车辆两端。如图2(a)所示,在列车中间对车布置3个测压面,数据分析时取中间3个截面计算结果的平均值。图2(b)所示为每个测压面的测点布置,考虑测量结果的准确性、车辆横截面尺寸和车辆模型内的走线情况,每个测压面上布置40个风压测点,共200个风压测点。
1.2 测试仪器
试验分为两部分:桥梁刚性模型的静力实验和车辆模型的测压实验。
静力实验是通过连接于桥梁模型两端的杆式五分量测力天平测得系统整体的气动力。测力天平可以测得横桥向、竖桥向两个方向的力及横桥向、竖桥向和纵桥向三个方向的力矩分量。梁体通过测力天平与转盘相连,并通过电机驱动转盘来精确控制来流与试验模型的夹角,即风攻角α。
测压试验的测试对象是车辆,在测试时通过螺栓将车辆固定在桥梁或路基的表面,采用美国PSI公司的电子压力扫描阀测试车辆表面的风压。压力采集设备为美国PSI公司生产的4个ESP-64HD微型压力扫描模块,可实现256个点的高速同步测压。采样时长是80 s,采样频率为312.5 Hz。
试验中,车辆和桥梁相接触。通过测压试验得到车辆的三分力,通过测力试验得到车桥系统整体的三分力,最后通过力的合成定理计算得到作用在桥梁上的三分力。
1.3 实验工况
选用CRH2型高速列车和大风区常用的箱梁、T梁和路基作为研究对象,测试风屏障对提高列车安全性能的影响。参考文献[10],选取高度为3.5 m、透风率为30%的圆孔式风屏障,分析不同工况下车辆和桥梁的气动力,表1所列为试验的工况安排,按照不同的线路架构形式、风屏障位置、立车行车位置、风攻角、风速等,共设计了318个吹风工况。

表1 试验工况Tab.1 Test cases
2 试验结果与分析
2.1 三分力系数
不同风攻角下作用在模型上的气动力可用三分力描述,即侧力FD(α)、升力FL(α)和力矩M(α),M(α)作用在模型的几何形心,三分力系数计算如式所示
(1)
式中:CD(α)、CL(α)、CM(α)分别是风轴坐标系下的侧力系数、升力系数和力矩系数;α为来流攻角(°);U为来流风速(m/s);ρ为空气密度(ρ=1.225 kg/m3);H、B和L分别为节段模型的高度、宽度和长度(m)。
2.2 线路结构形式的影响
箱梁、T梁和路基的存在会不同程度地影响列车周围的风场,因此将箱梁、T梁和路基三种不同线路结构形式下车辆的气动力进行对比。
表2所示为风攻角α=0°时,不同线路结构形式下的车辆三分力系数测试结果。可以看出:①风速分别为8 m/s、9 m/s和10 m/s时,相同线路结构形式上车辆的三分力系数都比较接近。即当风速在一定范围内变化时,其对车辆气动力特性的影响较小,可以忽略。因此,可取不同风速下车辆三分力系数的均值进行分析。②车辆在不同线路结构上的力矩系数都很小,对车辆影响可以忽略,车辆安全性主要由侧力系数和升力系数控制。对比侧力系数和升力系数可知,当车辆在路基上运行时最安全。而车辆在不同线路结构形式上的力矩系数都很小,接近零。
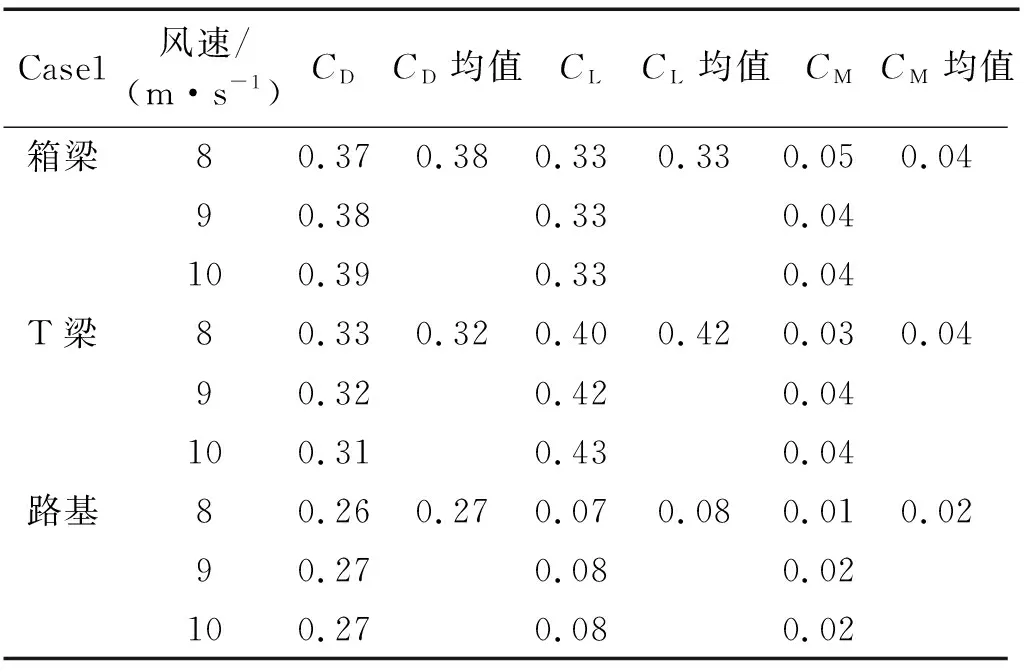
表2 车辆三分力系数Tab.2 Tri-component coefficients of vehicle
图3给出了箱梁和T梁上车辆三分力系数随风攻角的变化规律。从侧力系数上看,列车在箱梁和T梁上时侧力系数随风攻角先减小后增大。但车辆在箱梁上时,CD的最小值出现在α=-2°,而在T梁上时,CD在α=+2°时最小。升力系数CL随风攻角的增加而线性减小,在-2°附近相等。但是由于箱梁和T梁的截面形状不同,当风攻角大于-2°时,箱梁上车辆的CL减小更迅速。与升力系数相反,力矩系数随风攻角的增加而增加,且在-2°附近时两者最为接近。箱梁的力矩系数增加了161%,T梁的增加了77.6%。
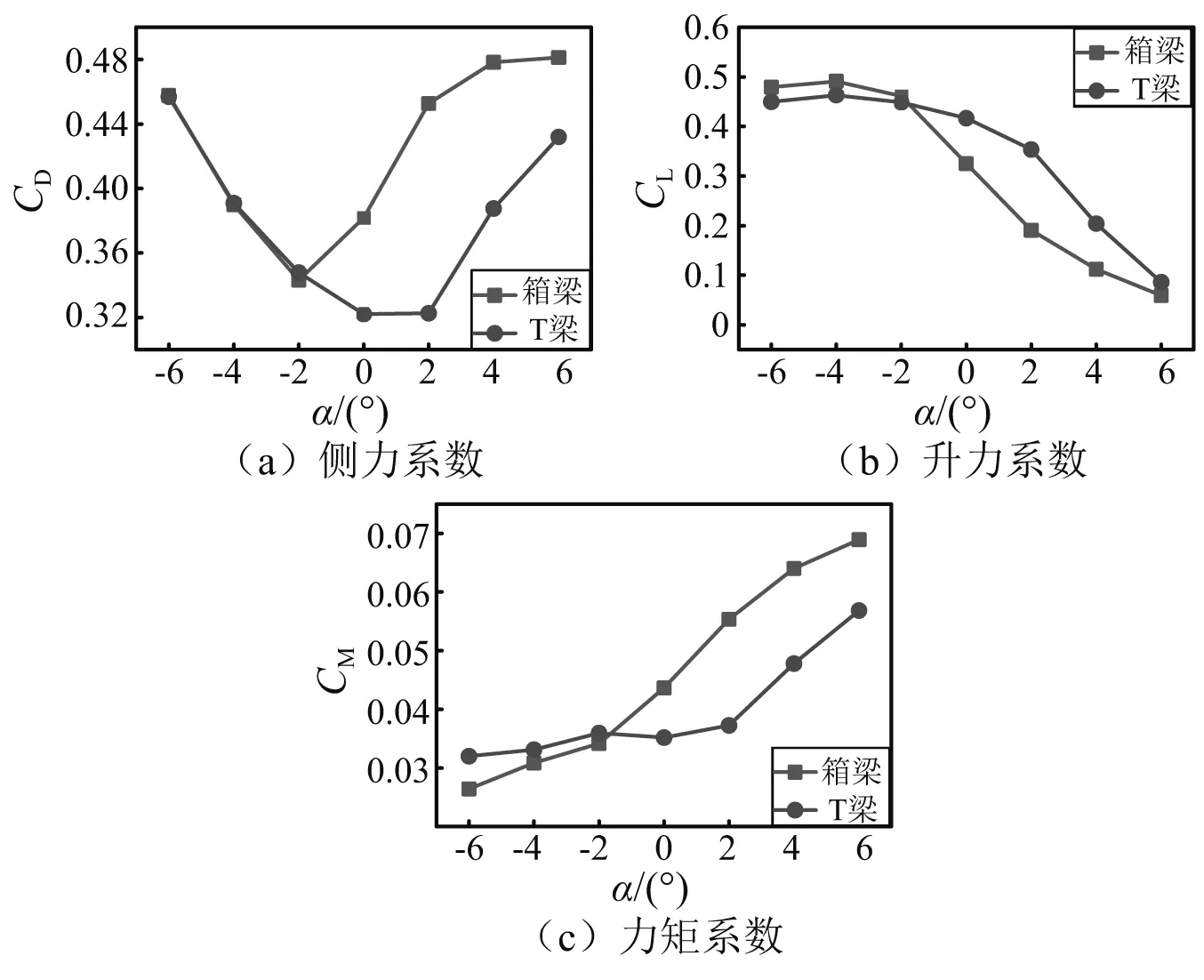
图3 车辆在不同梁型上的三分力系数Fig.3 Tri-component coefficients of vehicle at different bridges
2.3 风屏障位置的影响
选取箱梁这一典型的结构形式,分析车辆位于迎风侧和背风侧时,风屏障安装位置(在迎风侧安装单侧风屏障和安装双侧风屏障)对车桥系统气动特性的影响。
图4(a)给出了不同风攻角下箱梁上安装单侧风屏障和双侧风屏障时迎风侧车辆三分力系数的变化规律。对比可知,风屏障安装位置不同时,车辆的气动力系数都很接近。只有风攻角在-2°~+4°范围内且安装双侧风屏障时的CL略小于安装单侧风屏障时的CL。这是由于当来流经过迎风侧的风屏障时,只有部分气流穿过,其余气流在风屏障顶部和桥梁底部发生绕流,而作用在车辆表面的气流在车顶和车体迎风面的交界处又发生二次绕流,因此经过迎风侧风屏障和列车的双重阻挡作用后,位于背风列车区域的风场已经较弱。在背风侧安装孔隙式风屏障对此区域流场的影响较小。因此,安装双侧风屏障对车辆气动力影响很小。
图4(b)给出了不同风攻角下背风侧车辆三分力系数的变化规律。对比可知,安装双侧风屏障后背风侧列车的CD都大于安装单侧风屏障时的值,而CL在-6°~+2°范围内也都大于单侧风屏障的情况,风攻角为+4°和+6°时,安装单侧风屏障时较大,分别比安装双侧挡风屏时大37.4%和23.1%。在任何风攻角下,两者的CM很接近,安装背风侧风屏障对力矩系数的影响可以忽略。这是由于背风侧风屏障的存在使得列车下游的风场减弱,而对迎风侧风屏障和列车之间的风场影响很小。
图5(a)给出了在不同位置安装风屏障且车辆位于迎风侧时桥梁三分力系数随风攻角的变化规律。可以看出,桥梁的侧力系数随风攻角的增加持续增加,且安装双侧风屏障时的CD一直大于安装单侧风屏障时的CD。α在-2°~+6°时,双侧风屏障时桥梁的升力系数小于单侧风屏障时的升力系数。力矩系数基本相等,且数值随风攻角变化较小,但风攻角从-6°到+6°时,单侧风屏障和双侧风屏障时桥梁的CM增幅都很大,分别为96.7%和159%。背风侧风屏障的存在增大了桥梁的迎风面积,但由于迎风侧风屏障和车辆对侧风的双重阻挡作用,作用在背风侧风屏障上的力明显减小。

图4 车辆三分力系数Fig.4 Tri-component coefficients of vehicle
图5(b)给出了车辆位于背风侧时桥梁三分力系数随风攻角的变化规律。可知,α在-2°~+6°时,桥梁的三分力系数均比较接近。而在-6°~-4°时,安装双侧风屏障的CD和CM偏大,而CL偏小。由于背风侧风屏障距离背风侧列车较近,因此列车位于背风侧时,背风侧风屏障的存在对风场的影响较小,只是在某些风攻角下对桥梁的气动特性有所影响。
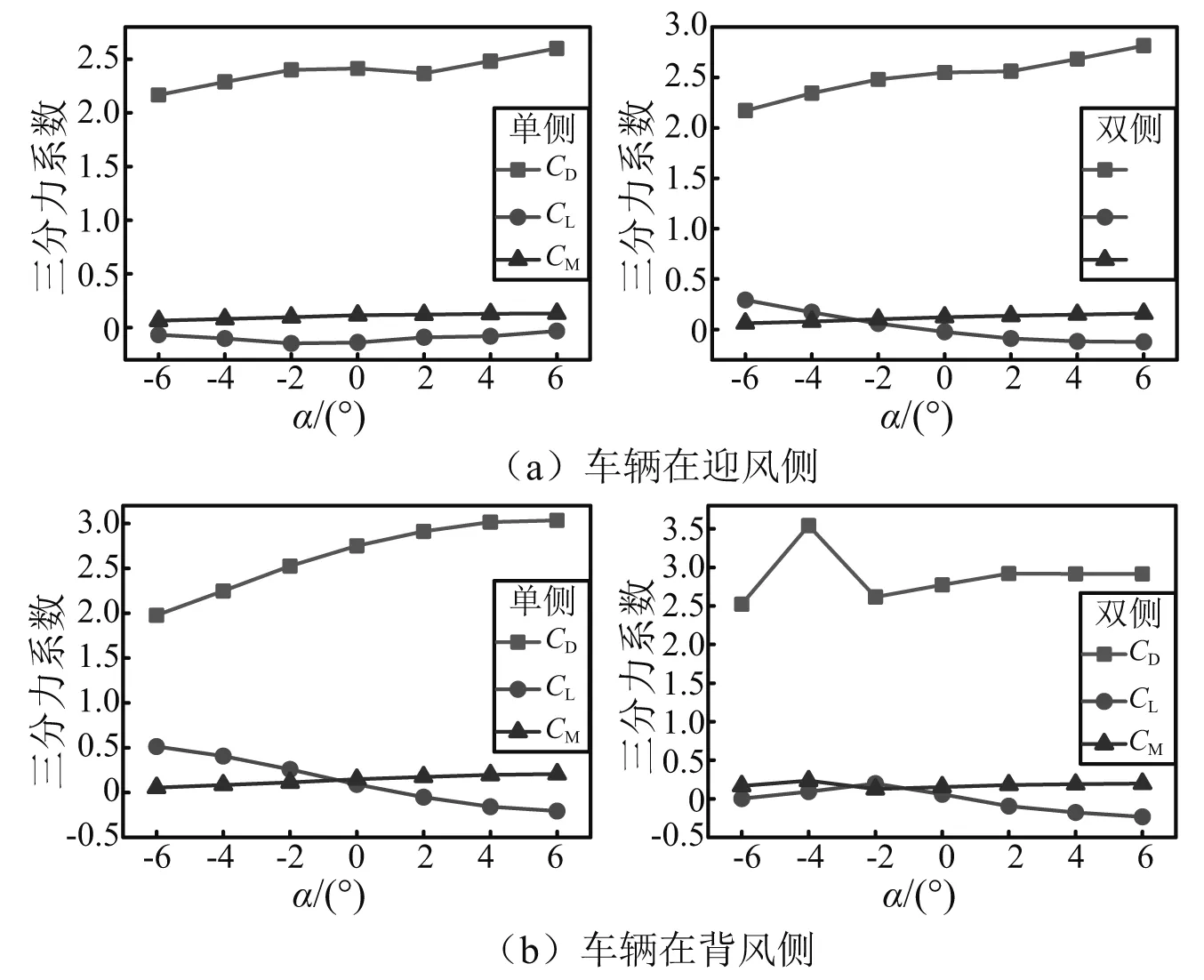
图5 桥梁的三分力系数Fig.5 Tri-component coefficients of bridge
2.4 行车位置的影响
双线铁路一般会存在双车的情况,迎风侧车、背风侧车和桥梁之间存在不可忽略的气动干扰效应。以安装单侧风屏障的箱梁为分析对象,单车(包括迎风侧车和背风侧车)和双车时车桥系统的气动力系数如表3所示。
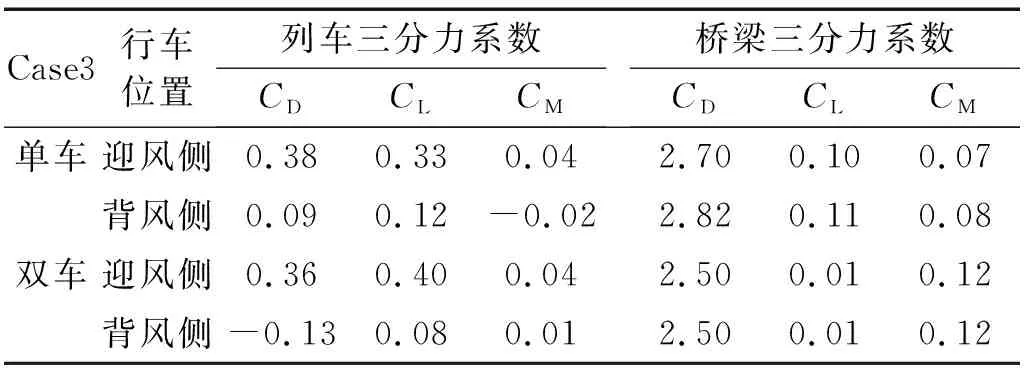
表3 不同行车位置时的车桥三分力系数Tab.3 Tri-component coefficients of train-bridge system α=0°
从表3中可以看出,单车时,迎风侧车的气动力系数都大于背风侧车,而桥梁的气动力系数都略微偏小。双车存在时,迎风侧车的气动力系数仍然大于背风侧车,桥梁的气动力系数基本不变。背风车的存在使得迎风侧车的CD减小了5.3%,但CL增加了21.1%。迎风车的存在使得背风侧车的CD和CL分别减小了244.4%和33.3%,而CM增加了33.3%。
图6(a)所示为单车和双车时迎风侧车的三分力系数随风攻角的变化规律。可见,有无背风侧列车时,车辆的气动力系数随风攻角的变化趋势一样,数值也基本相同。这是由于迎风侧车的下游区域风速较小,背风侧车对迎风侧车的气动干扰较小,亦即背风侧车的存在对迎风侧车的气动特性影响较小。
图6(b)所示为单车和双车时背风侧车的三分力系数随风攻角的变化规律。可看出,迎风侧车对背风侧车的三分力系数影响较大,尤其明显的是侧力系数。双车存在时,背风侧车的侧力系数明显减小,甚至有负数的情况,这是由于迎风侧车的遮风效应减小了背风侧车上的风荷载,以至受到“吸引”作用。在所有风攻角情况下,背风侧车的升力系数也小于双车时。
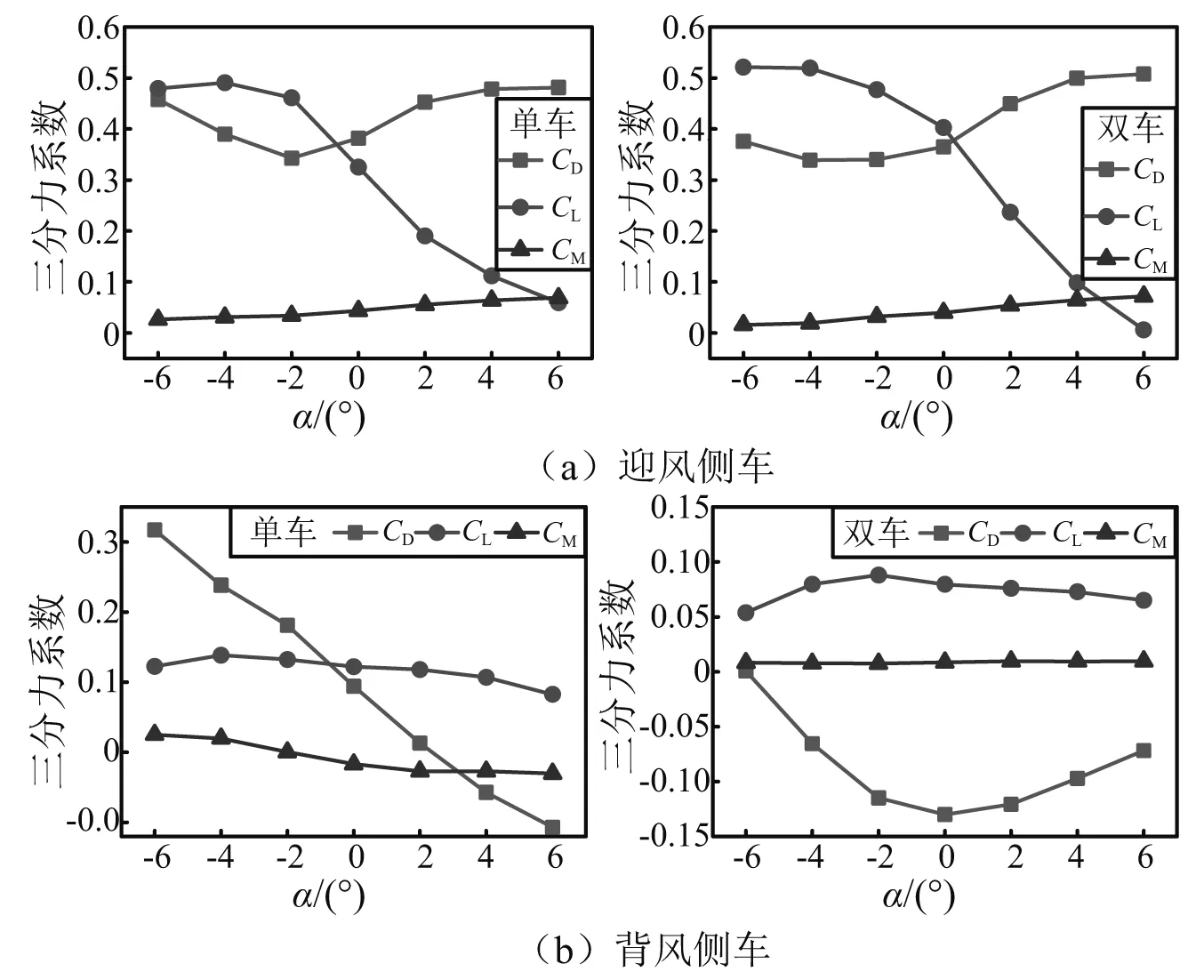
图6 车辆三分力系数Fig.6 Tri-component coefficients of vehicle
图7所示为单车(迎风侧车和背风侧车)运行和双车3种工况下的桥梁三分力系数。可以看出,随着风攻角的增大,桥梁的侧力系数和力矩系数也都随之增大,相反升力系数随之减小。当风攻角大于-2°时,背风侧行车的桥梁CD和CM最大,而迎风侧行车时最小;在-6°~-2°时,三种行车工况下桥梁的CD和CM较为接近。三者的CL在+3°附近相等,当风攻角大于+4°时,迎风侧行车时桥梁的升力系数又成为最大值。这是由于风攻角改变后,迎风侧车和背风侧车与桥梁之间的流场发生改变,气动干扰效应也发生相应变化。

图7 桥梁的三分力系数Fig.7 Tri-component coefficients of bridge
3 CFD数值模拟
对风洞缩尺模型的测试精度进行对比验证,选取安有单侧风屏障的车-桥系统进行CFD数值模拟,车辆分别位于迎风侧和背风侧。建立三维数值模型,数值模型的尺寸与风洞试验中模型的尺寸相同,计算域的尺寸为8.4 m×4.4 m×0.4 m,网格采用六面体网格形式,数量为1 042万。采用RNGk-ε湍流模型,设定来流面为速度入口边界条件,出口为静压为零的压力出口边界条件,上表面为滑移壁面,地面为无滑移壁面,风速取为10 m/s,计算结果列于表4中。
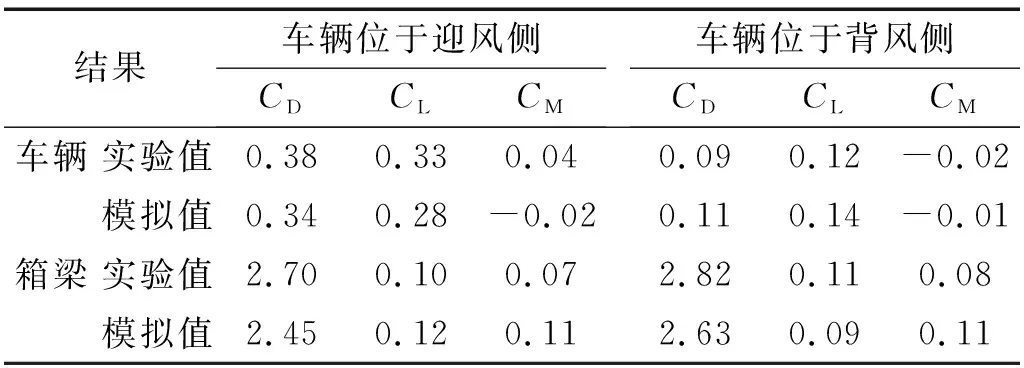
表4 风洞试验与数值模拟结果对比Tab.4 Comparisons ofresults from tests and simulation
从表4知,数值模拟与试验得到的CD和CL较为接近,挡风屏后风场复杂且CM本身较小,因此差别稍大。
图8所示为车桥系统的压强分布云图。从图中可知风屏障的存在改变了车桥系统周围的流场,侧风直接作用在风屏障上,风屏障无孔处的压强最大值为70 Pa左右,而在开孔位置气流流速加快,使得列车迎风面的压强成为负值。风屏障和列车迎风面之间的涡流变化复杂,压强最小值出现在列车迎风面和上表面交界处,约为-140 Pa。且在车桥系统的下游出现了较大漩涡,漩涡不断地脱落。
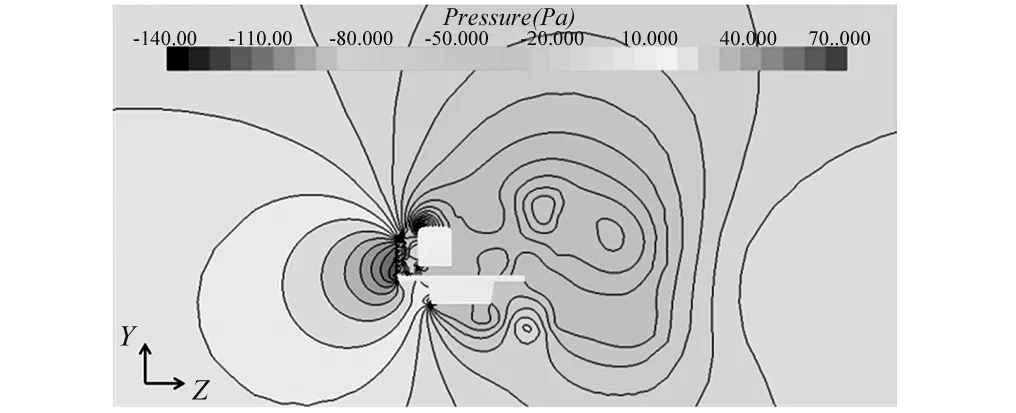
图8 压强分布云图(Pa)Fig.8 Contour of pressure distribution (Pa)
4 列车安全性分析
高速列车在强侧风下发生倾覆,主要是高速列车的侧力、升力和二者共同产生的侧倾力矩过大造成的,其中侧倾力矩是衡量列车横风稳定性最重要的指标,为便于分析,转换成侧倾力矩系数[11]。如图9所示,将实验得到的作用于列车几何形心的三分力转换到作用于左右轮轨接触轴线上的力矩Ml和Mr,再进行无量纲化,即可得到CMl和CMr。
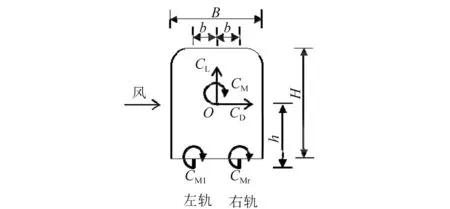
图9 侧倾力矩系数Fig.9 Rolling moment coefficient
左右轨线上侧倾力矩系数的计算如式(2)所示
(2)
式中:CD、CL、CM分别为相对于车辆形心的侧力系数、升力系数和力矩系数;b为车辆形心至轨道的水平距离(m);h为车辆形心至轨道的垂直距离(m)。
在不同线路结构形式和风屏障位置下,左右轨线上的侧倾力矩系数,如表5所示。
由表5可知,右轨线上的侧倾力矩系数总是大于左轨上的侧倾力矩系数。在不同线路上时,列车的CMl基本相同,而在箱梁上时CMr最大,而在路基上的侧倾力矩系数最小。相对于单侧风屏障的情况,安装双侧风屏障并没有有效改善列车的抗侧倾能力,相反却使列车相对于右轨线的侧倾力矩系数略微增大。

表5 车辆的侧倾力矩系数Tab.5 Rolling moment coefficients of vehicle
5 结 论
针对高速列车在箱梁、T梁和路基三种不同结构形式上运行的系统模型进行节段模型风洞试验。对实验结果进行分析可以得出如下结论:
(1) 当风速在一定范围内变化时,风速对车辆三分力系数的影响较小,可以忽略。较于箱梁和T梁,列车在路基上运行时的侧力系数、升力系数和力矩系数均最小,行驶较安全。
(2) 安装单侧风屏障和双侧风屏障时,车辆的气动力系数都很接近。只有风攻角在-2°~+4°范围内且安装双侧风屏障时CL略小于安装单侧风屏障时的CL。背风侧风屏障的存在增大了桥梁的迎风面积,但是由于迎风侧风屏障和车辆的遮风效应,作用在背风侧风屏障上的气动力明显减小。
(3) 双车存在时,迎风侧车的下游区域风速较小,背风侧车对迎风侧车的气动干扰较小,而迎风侧车对背风侧车的气动特性影响较大。在不同行车工况下,桥梁的侧力系数和力矩系数也都随风攻角增大而增大,相反升力系数随之减小。
(4) 数值模拟与实验得到的CD和CL较为接近。风屏障的存改变了作用于迎风侧车周围的风场,并且在车桥系统下游产生较大漩涡。
(5) 车辆对右轨线的侧倾力矩系数总是大于对左轨线的侧倾力矩系数。在不同线路上时,车辆的CMl基本相同,而CMr在箱梁上时最大。安装双侧风屏障并没有明显改善列车的抗侧倾能力。

