基于脊线信息增强与特征融合的瞬时转频估计
江星星, 吴 楠, 石娟娟, 沈长青, 李 川, 朱忠奎
(1.苏州大学 城市轨道交通学院, 江苏 苏州 215131;2.重庆工商大学 制造装备机构设计与控制重庆市重点实验室, 重庆 400067)
阶次跟踪是变工况设备故障诊断常用分析方法之一[1],其关键在于准确地获取等角度重采样的时刻,将时域内的非平稳信号转化为角度域内的平稳或循环平稳信号。硬件阶次跟踪[2]和计算阶次跟踪[3]是两种传统的基于转速计阶次跟踪方法,但转速获取装置的成本及安装制约着这些方法的使用范围。基于时频分布的无键相阶次跟踪方法是近年来提出的新的阶次跟踪技术,其依靠从设备动态信号的时频分布中提取出参考轴的转频信息,进而实现等信号的角度域重采样[4-5]。
时频分布提供了设备信号的时间-频率联合信息,能够全面地描述信号频率随时间变化的关系。为此,可以基于特征频率的分布特性提取转频。许多学者基于信号时频分析提出了相关的瞬时转速识别方法。如彭富强等[6]采用线调频小波路径追踪算法估计瞬时转频;Wang等[7]采用Wigner-Will变换对轴承振动信号进行时频分析,然后基于相对互信息原理对故障特征频谱进行自适应提取;Shi等[8]利用广义逐步解调变换和同步挤压算法增加时频聚集性,提高了瞬时频率的提取精度;Urbanek等[9]首先通过时频分布粗糙估计转频,然后对重采样带通滤波信号反采样获取精确瞬时转频。以上研究为提取变速机械设备转速信息提供了新的途径。需要指出的是,一些新的时频分析方法虽然可以提高信号时频表示的可读性,但是会带来算法计算复杂,时效性欠佳等问题[10-11]。而短时傅里叶变换(Short Time Fourier Transform, STFT)、小波变换等时频分析方法虽然可以简单、快速地得到信号的时频分布特征,但是因海森伯格不确定原则以及目标时频脊线能量微弱等原因,造成这类时频分析方法得到的时频表示聚集性差以及峰值搜索等算法对时频表示结果中的转频信息提取不够准确。
考虑到STFT分析方法的简单、快速特性,适用于工程信号分析,本文将建立基于脊线信息增强与特征融合的瞬时转频估计方法,以克服基于STFT提取转速信息方法的缺陷,实现快速、准确地从STFT分析结果中获取设备转速。首先给出幅值累加平方的时频特征增强策略;然后从机械故障信号的低频段、共振频段分别预估计出转频;再建立基于脊线概率分布和局部波动特征的信息融合准则对提取的两类转速相关信息进行融合以准确获取转频。
1 基于STFT的时频表示特征增强
时频分布中时频脊线是转频提取的关键信息,而时频脊线主要由机械系统的转频及其倍频成分组成。强背景噪声干扰下,时频脊线信息往往难以有效提取,且时频脊线的可视化较差,无法预先通过时频脊线对转频信息进行准确评估。考虑到转频及其倍频成分具有确定性,而噪声成分具有随机特点,本文首先建立整数倍幅值累加平方策略来增强目标脊线。
机械设备的转频及其倍频成分可表示为多分量谐波信号x(t):
(1)
式中:M为谐波分量个数;f0为瞬时转频。
x(t)的STFT表示为
(2)
式中:h*(ω)为窗函数的频域形式。
对时频表示结果进行整数倍累加,第k个时频脊线分量的幅值累加结果为
(3)
其中k∈[1,M],(τm,ωn)时频点处的累加幅值为
(4)
此外,假定时频点(τm,ωn)附近处的噪声成分表示为N(τm,ωn′),则时频点(τm,ωn′)处噪声幅值累加结果为
(5)
式(4)和式(5)分别为幅值累加之后目标时频点和噪声点的结果。因为目标时频点与倍频成分之间的确定性关系和随机噪声成分累加后强噪声时频点处会引入能量较弱的噪声分量等因素,所以时频分析幅值整数倍累加之后目标时频脊线的能量增强效果相比于噪声成分更为显著。另外,一般目标时频脊线的能量相对于其附近的随机分量要突出[12]。为此,经过幅值累加操作后满足:
(6)
进一步,幅值累加结果的平方处理为
(7)
(8)
令幅值累加以及幅值累加平方的目标时频点幅值与其附近噪声点幅值之比分别为
(9)
(10)

下面构建一仿真信号来验证幅值累加平方策略对有用信号的增强效果。
仿真信号为x(t)=x1(t)+x2(t)+η(t),其中x1(t)为故障成分,x2(t)为转频同步成分,η(t)为噪声成分。其中x2(t)=cos[2π×(1.25t2+15t)]+0.5×cos[4π×(1.25t2+15t)]+0.4×cos[6π×(1.25t2+15t)];η(t)为高斯白噪声(信噪比为-5 dB)。则仿真信号的转频x(t)为:f=1.25t2+15,设定采样频率为20 K,采样时间3.5 s。
仿真信号的STFT时频分析结果如图1(a)所示。采用幅值累加的时频表示结果如图1(b)所示。采用幅值累加平方策略进行时频增强的结果如图1(c)所示。对比以上结果可以直观地看出,经过幅值累加平方处理的时频表示结果中的转频相关成分与噪声成分之间的能量差异最显著。
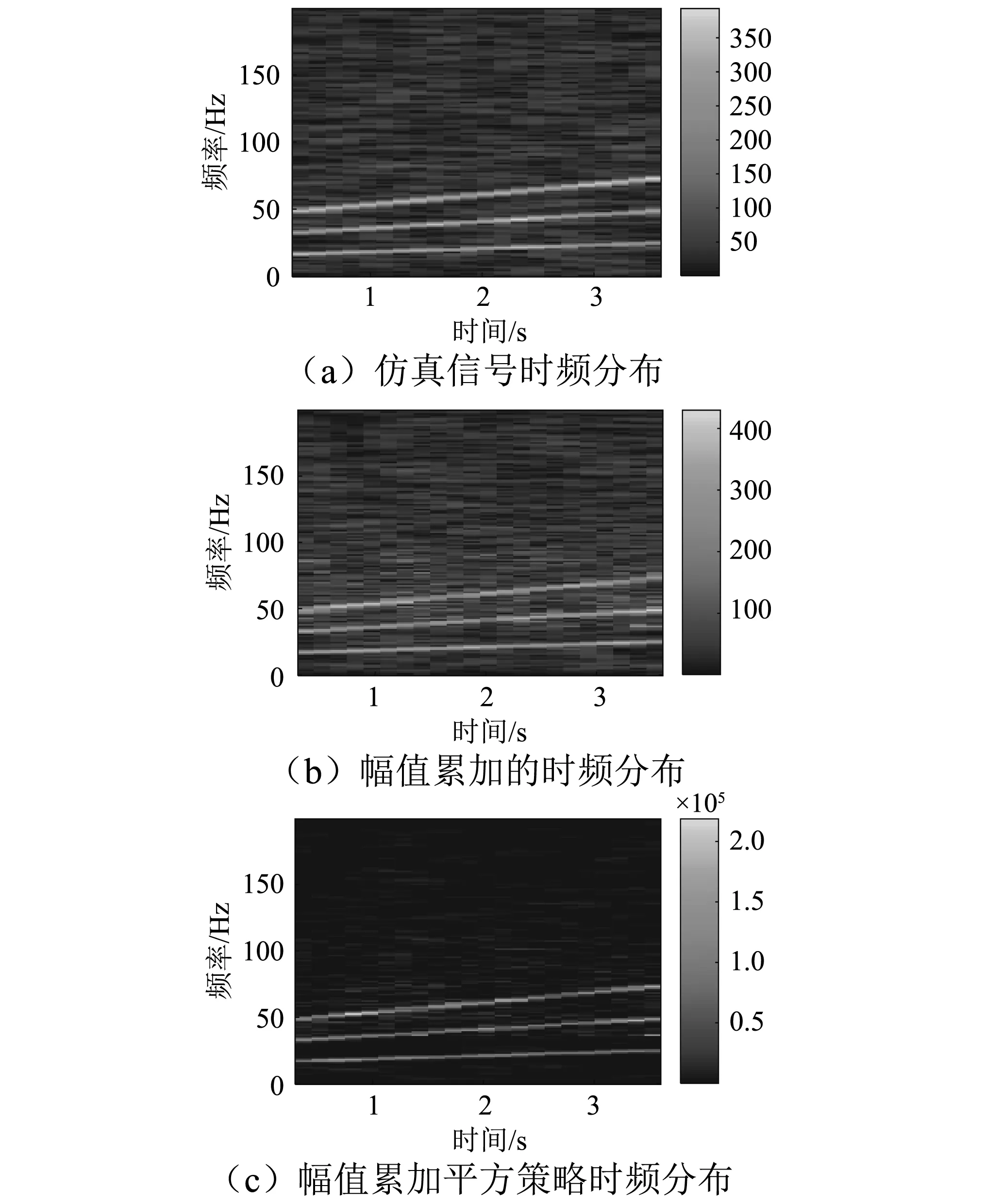
图1 仿真时频表示增强Fig.1 Enhanced TFD of the simulated signal
2 基于概率分布和局部波动特征的融合准则
变工况下,因机械运行状态复杂,设备动态信号中有效成分的能量随时间变化产生波动,尤其在启停及负载变化阶段各种噪声的干扰也变得更加剧烈,导致信号低频区域中与转轴同步的脊线信息被淹没在噪声源中[13],以至于仍难以从增强的时频表示中提取完整的瞬时频率曲线。当设备中的关键部件出现损伤时,局部冲击特征会激励起系统固有频率,相应设备动态信号中包含共振频带,共振解调的包络信号中会包含与转频同步的脊线信息。也即,通过共振解调的包络信号来提取转速信息,可是这种方式提取转速相关的脊线同样容易受到噪声干扰。考虑到信息融合技术具有保留有效信息、去除异常数据的特点,从而将其引入来融合设备动态信号的低频区域脊线和共振解调包络信号中脊线的有效信息,达到提升识别结果准确性的目的。
2.1 瞬时频率预提取与同步化
对于提取低频段中与转轴同步的脊线信息时,只需要对包含转频及其倍频成分的频段进行时频分析;对于提取共振频段中的脊线信息时,则需要先确定所需分析的共振频段范围,然后提取共振解调包络信号中的转频同步脊线信息。具体操作流程如下。
(1)分离振动信号x(t)中的低频段。低频段的频率选取范围为[0,f0]。本文取500 Hz可以涵盖常见工况下旋转轴转频及其倍频信息。
(2)提取振动信号的共振频段[fa,fb]。对于共振频带的选取,可以通过轴承结构参数来确定,然而这样操作需要一定的先验知识,难度较大。在此,引入经典的快速峭度谱方法来高效地识别出共振频带。
(3)利用STFT处理振动信号x(t)的低频段x1(t)和共振频段信号x2(t),得到的时频结果分别为Sx1(τ,ω)和Sx2(τ,ω)。
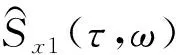
(5)采用峰值搜索算法[11]从增强时频表示结果中搜索与转频同步的脊线。
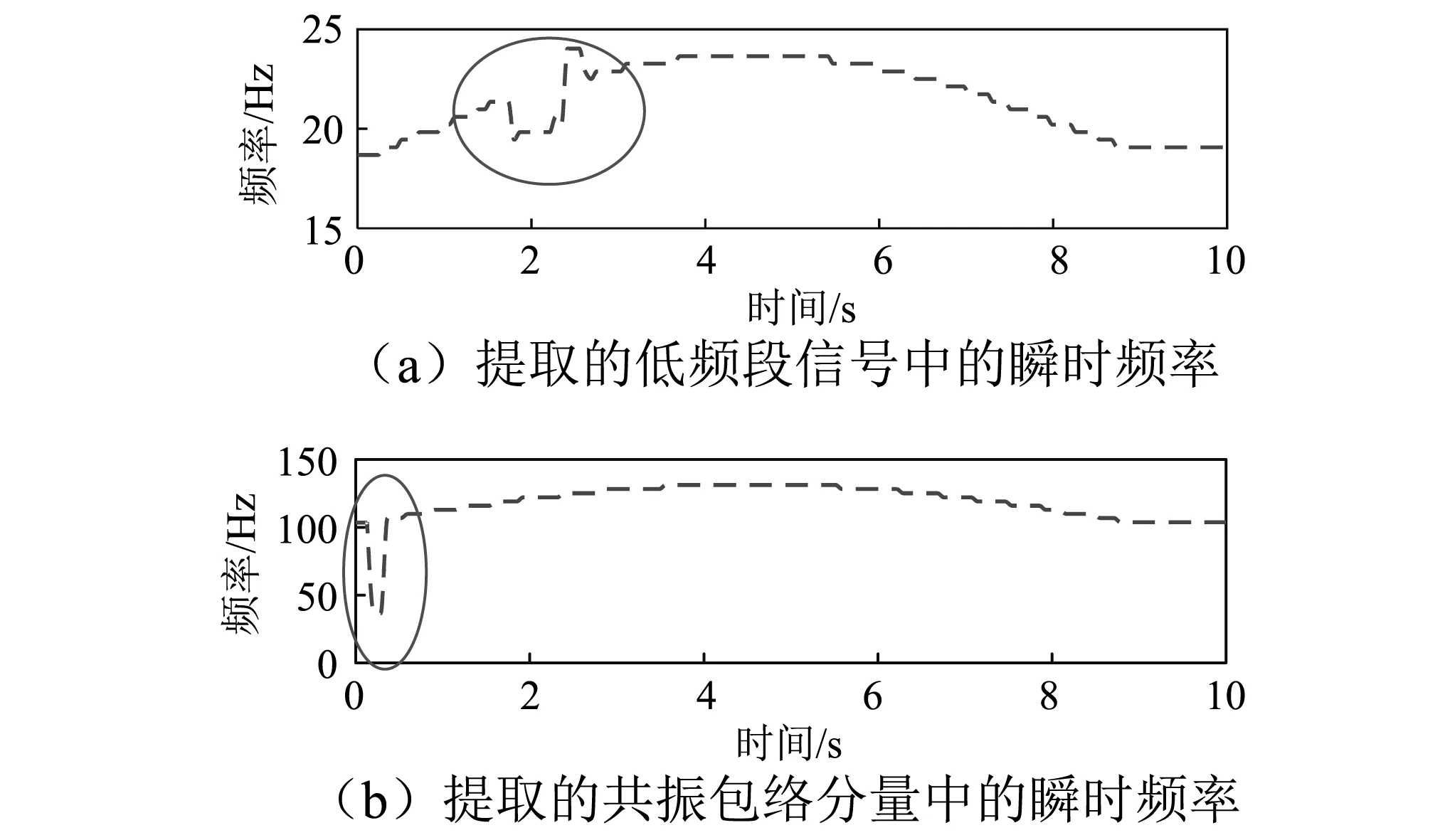
由于旋转机械系统可能存在轴不平衡、不对中等问题,时频分布中与转频同步的脊线信息会成倍频出现,提取出的能量最大的同步脊线不一定是转频曲线。因此在提取低频段转频脊线时,需已知转频大致所在范围,以便对结果进行校正。至此,可以预估计出低频段和共振频段的瞬时频率曲线,分别为Px1(τ,f),Px2(τ,f)。
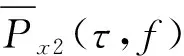
(11)
式中:k为同步化参数。参数k可以依据重合度R来确定
(12)
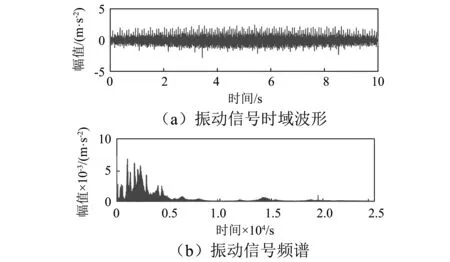
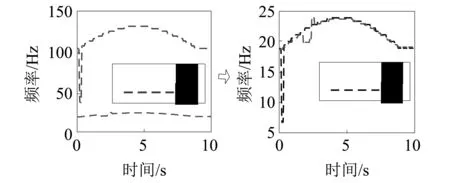
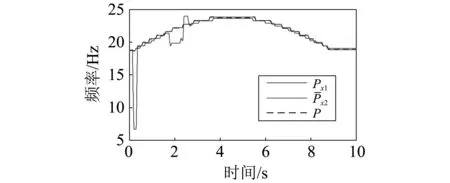
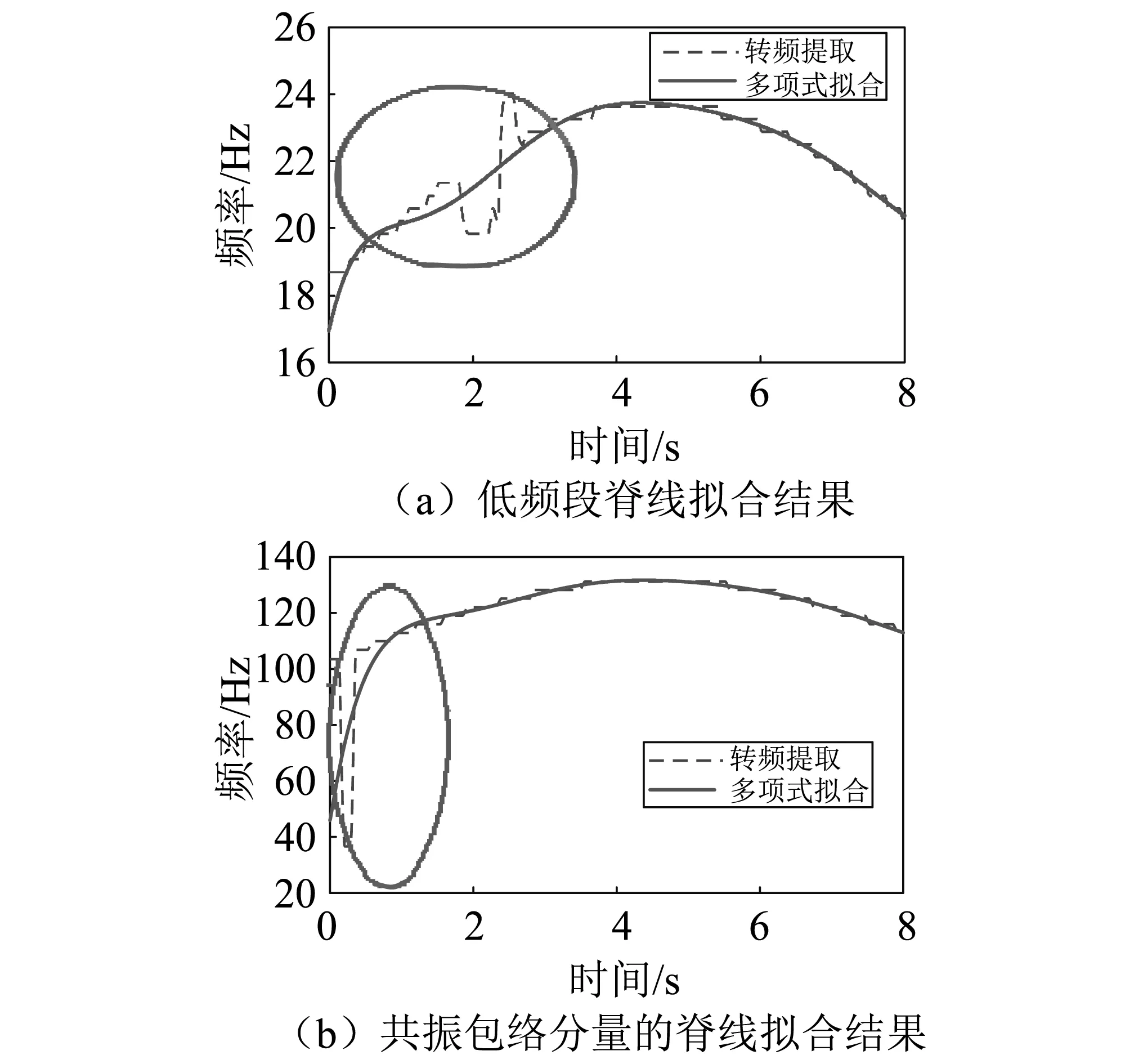
式中:R取极小值时对应的k为所需的同步化参数,且0 由于噪声成分的干扰,从低频段和共振包络信号中提取的脊线结果中部分脊线区间会出现失效现象。融合技术具有保留有效信息的特性。为此,通过对低频段和共振包络信号提取的脊线进行融合,可在一定程度上改善失效脊线的结果。定位异常脊线所在位置是脊线融合的关键点之一。如果脊线不失效,那么同步化后两脊线应该保持一致。因此可以利用脊线的差值信息来反应两者之间的差异,也即差异信息能够指示脊线失效位置。 (13) 理论上,如果提取的脊线为有效结果,那么的值为0。实际上,由于两条脊线都存在一定的失效位置,ΔC(τ)会出现非零值。因此,可以通过ΔC(τ)值的变化来判断异常脊线的位置。 一般脊线出现异常,会以异常区间的形式出现,并且由一对上升沿和下降沿确定。异常区间即为所需融合的区间P(τK,τL)。根据ΔC(τ)的信息来定义融合区间的上升沿τK和下降沿τL位置: τK=τn,if(ΔC(τn)≤ξ)与(ΔC(τn+1)>ξ) (14) τL=τn,if(ΔC(τn)>ξ)与(ΔC(τn+1)≤ξ) (15) 式中:ξ为确定异常区域的阈值。在此考虑采用概率分布的方式来确定阈值ξ。 ξ=ΔC(τ) s.t. max(Pdf(ΔC(τ))) (16) 式中:Pdf(ΔC(τ))表示ΔC(τ)的概率分布。max(Pdf(ΔC(τ)))表示概率统计最大值。也即表明阈值ξ取概率统计最大值位置的脊线差值频率。本文通过概率统计方式确定阈值的优势在于:避免阈值ξ取值过小造成融合区间过多、计算效率下降;避免阈值t取值过大融合不充分,遗漏融合区间;相比人为判定阈值的物理意义更显著。 (17) (18) 至此,得到数据融合后的瞬时转频估计结果。 围绕上述分析,在此建立一种基于脊线信息增强与特征融合的瞬时转频估计方法。该方法的流程图如图2所示。具体内容如下: 1)基于幅值累加平方策略对时频分布特征进行增强; 2)预提取机械故障信号的低频段、共振频段中的时频脊线,并将它们同步化; 3)利用同步化的两类转速相关脊线差值结果的概率分布信息,对异常融合区间进行定位。 4)建立局部波动特征的融合准则对异常融合区间进行融合,以校正预估转频中的异常区间,实现转频的准确获取。 图2 提出的瞬时转频估计方法流程图Fig.2 The flow chart of the proposed method 为检验本文所提方法的有效性,本文将该方法应用于包含轴承局部损伤故障的旋转机械实验信号的瞬时转频提取。试验系统如图3所示[14],驱动电机(SIEMENS, 3~, 2.0HP)通过联轴器连接主轴(Ø30 mm)。轴两端由两个双列球轴承支撑。2个质量盘安装在两支撑轴承间以提供负载。加速度传感器(PCB ICP 353C03)安装在1号轴承座顶部以测取振动信号。支撑轴承型号为SKF 1207 EKTN9/C3,每排滚珠个数Z=15,滚动体直径d=8.7 mm,接触角α=0°,轴承节径D=53.5 mm。利用点火花技术,在图4所示轴承内圈上设置了直径为0.9 mm的点蚀故障。 图5(a)为采集的轴承内圈故障振动信号,采样频率fs=25.6 kHz,采样时间t=10 s。旋转轴的转频fc在15~25 Hz之间波动。图5(b)为图5(a)所示振动信号的频谱。首先通过低通滤波获取低频段信号,滤波频带为[0,500 Hz],再利用快速谱峭度算法提取共振频段成分[14]。由图6可知,共振频段集中在第3层的[12 500,15 600 Hz]频段。然后对该共振频带信号进行包络解调,得到包络信号。进一步,利用STFT方法分析低频段信号和共振解调包络信号,得到如图7(a)和8(a)所示的时频表示结果。原始时频表示的幅值累加平方增强结果如图7(b)和8(b)所示,可以看出特征增强的时频表示中噪声成分得到了有效抑制。再进一步,采用峰值搜索算法[15]对图7(b)和8(b)所示的时频谱进行瞬时频率提取,并根据转频大致所在范围对提取的脊线结果进行校准处理,可以得到如图9(a)和(b)所示的转频同步信息Px1、Px2。图9(a)和(b)中的圆圈位置指示,通过低频段信号和共振解调包络信号得出的转频预估结果出现了异常波动。出现这种现象主要是因为相应时频脊线的能量微弱,且受到噪声干扰,而峰值算法的抗噪性能差,致使未能对有效脊线信息准确提取。 图3 旋转机械实验装置Fig.3 Exprimental set-up 图4 内圈故轴承Fig.4 Inner race defect bearing 图5 采集的实验信号Fig. 5 The collected vibration signal 图6 谱峭度分解结果Fig.6 Result obtained by spectral kurtosis 图7 低频区域信号时频表示Fig.7 TFD of the lower band component 图8 共振解调信号时频表示Fig.8 TFD of the demodulated envelope component 图9 预估计的瞬时频率Fig.9 IF estimation 图10 瞬时频率同步化Fig.10 IF synchronization 图11 融合区间定位Fig.11 Locating the fusion region 为了进一步说明本文方法具有的优势,在此利用曲线拟合方法对低频段和共振频段的转频脊线进行处理,结果如图13中实线所示(虚线表示原始提取转频脊线)。对比图12(虚线)和图13所示结果,可以发现本文提出方法能够有效地对异常数据段进行准确校正,而异常数据段的曲线拟合结果与真实目标脊线存在较大偏差,未能有效校正图中红色圆圈标注的异常数据段。这主要是因为曲线拟合等方法是一种对曲线整体表示的方法,难以兼顾到细节之处,且需要一定的先验知识来选择恰当的拟合阶次。然而,本文提出可以依靠定义的信息融合准则自适应地实现有效信息融合,并保留提取结果的局部细节之处。 图12 转频融合结果Fig.12 The estimated shaft IF 图13 时频脊线的拟合结果Fig.13 Curve fitting result of the time-frequency ridge. 针对传统的基于时频分布转速估计方法的准确性不足等问题,以快速、简单的STFT为基础,提出了基于概率分布与波动特征的旋转机械瞬时转频估计方法,并通过含轴承局部损伤故障的变转速机械试验信号验证了提出方法的有效性。 (1)相对于原始时频分布以及幅值累加时频分布,提出的幅值叠加平方策略获得的信号时频分布可读性更好、聚集性更优。 (2)分别从低频段信号和共振解调包络信号中同步提取瞬时频率信息,并建立了基于局部波动特征的融合准则。将二者进行融合,改善了原始脊线识别结果,提升了转频估计的准确性。 (3)引入了概率分布统计特征,来自适应地定位异常融合区间的阈值,使得提出的脊线融合方法具有自动完成融合过程的优点,以及物理意义更显著。 (4)在实际恶劣工况下,采集的机械信号内容十分复杂、背景噪声强、干扰成分多,会造成在低频带和共振频带预提的目标脊线结果与真实偏差较大、相互之间无法形成互补的优势,那么融合结果无法进行准确校正,需进一步去研究并引入更多元信息进行融合、来对异常段进行校正。2.2 基于概率分布的异常脊线区间定位
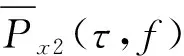
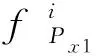
2.3 基于波动特征的脊线异常区间融合
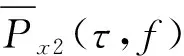
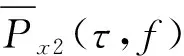
3 基于脊线信息增强与特征融合的瞬时转频估计方法

4 试验验证





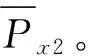

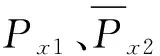
5 结 论

