基于VMD和样本熵的高压断路器故障特征提取及分类

万书亭， 豆龙江， 李 聪， 刘荣海

(1.华北电力大学 机械工程系，河北 保定 071003；2.云南电网有限责任公司电力科学研究院，昆明 650000)

作为电力系统中重要的保护与控制电器，高压断路器性能的可靠性关系到整个电网运行的安全与稳定，其运行维护也是电力部门日常工作的重要内容。目前电力系统多采用定期检修时进行预防性试验的方法来了解断路器的运行特性，这种做法不仅费时费力，而且频繁地操作和过度地拆卸检修会降低断路器的动作可靠性，带来一定的负面影响[1-2]。因此，加强机械故障诊断和在线监测方法的研究，提前发现潜在故障，对提高高压断路器的可靠性以及增强电力系统的安全性、可靠性和经济性具有十分重要的意义。

高压断路器在操作过程中产生的机械振动信号蕴含了丰富的信息，针对其振动信号展开分析可发现断路器操作机构的机械故障信息[3-6]。因此，基于振动信号的状态监测与故障诊断逐渐成为研究热点[7-13]。例如，梅飞等[14]提出了一种基于融合粒子群的模糊核聚类与支持向量机的故障诊断方法。吕超等[15]提出了一种具有在线自学习能力的断路器机械状态分类网络C-aiNet，相对于基于神经网络的故障诊断，分类更为精确。程序等[16]使用因子分析对特征量进行降维优化、支持向量机经粒子群参数寻优后对断路器的状态进行分类，取得了较好的效果。孙来军等[17]将小波包和特征熵相结合构造特征向量，利用BP申请网络进行分类，取得了较为实用的效果。孙一航等[18]提出基于经验模态分解能量总量法与支持向量机理论相结合的断路器振动信号的特征向量提取和故障分类的分析方法，实验结果表明该方法能够识别出振动信号的差别及故障类型。但这些诊断方法仍存在一定的不足，例如，小波包分析方法是预先选定基函数和分解尺度，这样得到的结果是某一固定频带的信号，而频带的范围只与采样频率有关，与信号本身无关；而经验模态分解存在模态混叠的现象，相同尺度出现在不同的本征模态函数中，该问题难以解决。

针对以上问题，本文研究了Dragomiretskiy等[19-21]提出的变分模态分解(Variational Mode Decomposition，VMD)对振动信号进行分解。该方法是一种自适应信号分解新方法，VMD为完全非递归分解模型且运算效率高，具有良好的抗噪性，克服了经验模态分解(Empirical Mode Decomposition，EMD)和局部均值分解(Local Mean Decomposition，LMD)在递归模式分解过程中的模态混叠、对频率相近的分量无法正确分离、受采样频率影响等不足。VMD分解模态稳定性好，能够很好地反映信号的奇异性特征，具有鲁棒性高的特点。

本文将变分模态分解和样本熵相结合，提出了一种应用在高压断路器振动信号特征提取的新方法。针对断路器的缓冲弹簧无效、分闸弹簧力减小、基座螺丝松动等故障进行模拟实验表明该方法能快速有效地提取断路器故障振动信号的特征向量并能正确地进行状态识别和分类，获得了较好的诊断效果。

1 变分模态分解

1.1 理论支撑

变分模态分解是Dragomiretskiy 等提出的一种信号处理的新方法，其核心思想是变分问题。该方法在获取IMF分量时不同于EMD 和LMD 算法所使用的循环筛分剥离的信号处理方式，而是将信号分解的过程转移到变分框架内，通过迭代搜寻变分模型最优解来确定每个分量的频率中心及带宽，从而能够自适应地实现信号的频域剖分及各分量的有效分离，突出了数据的局部特征，表现出更好的噪声鲁棒性，同时具有良好的采样效应。

VMD的分解过程即变分问题的求解过程，包括变分问题的构造和求解，其中变分问题具体构造步骤如下：

①通过Hilbert 变换，得到每个模态函数uk(t)的解析信号，目的是得到其单边频谱;②对各模态解析信号混合一预估中心频率e-jωkt，将每个模态的频谱调制到相应的基频带；③计算以上解调信号梯度的平方L2范数，估计出各模态信号带宽，受约束的变分问题如下：

(1)

式中：{uk}={u1, …,uk}为分解得到的K个模态分量，{ωk}={ω1, …，ωk}为各模态分量的中心频率。

为求取上述变分问题，引入二次惩罚因子α和拉格朗日乘法算子λ(t)，将约束性变分问题变为非约束性变分问题，其中二次惩罚因子可在高斯噪声存在的情况下保证信号的重构精度，拉格朗日算子使得约束条件保持严格性，扩展的拉格朗日表达式如下:

L({uk},{ωk},λ)=

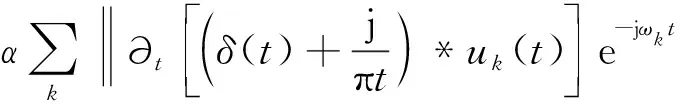
(2)

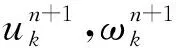
(3)

(4)

VMD实现过程如下:

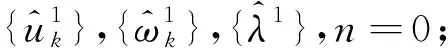
2)根据式(3)和式(4)更新uk和ωk;

3)更新λ:

1.2 基于VMD的仿真信号分析

为了验证VMD算法的优越性，对断路器理论仿真信号进行分析验证?断路器的振动信号由多个瞬态非稳定衰减振动事件组成，每个振动事件相当于一个IMF根据相关学者的研究成果[12]，理想的断路器振动信号模型如下:

(5)

式中:Ai为第个振动事件的最大振幅；αi为衰减系数；fi为振动频率；ti为起始时间；u(t)为单位阶跃信号。通过MATLAB仿真生成由振动事件组成的断路器振动信号，采样频率为10 kHz，各振动事件的参数如表1所示，波形如图1所示。

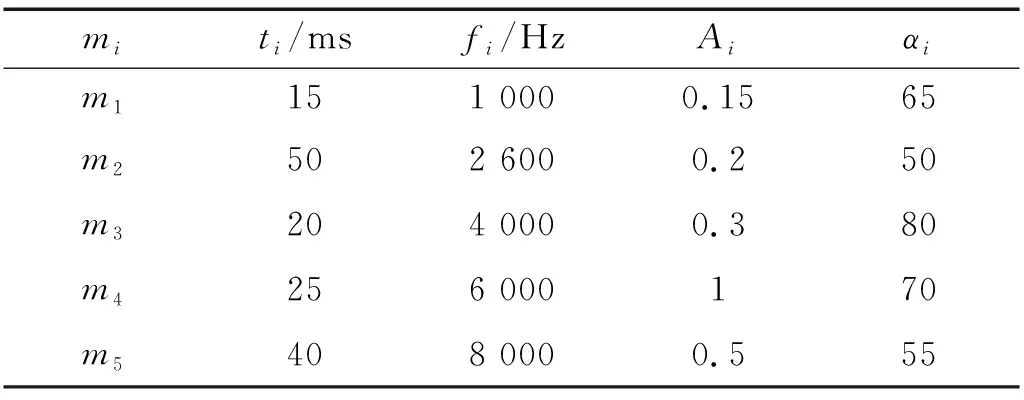
表1 仿真信号参数Tab.1 Parameters of the simulation signal

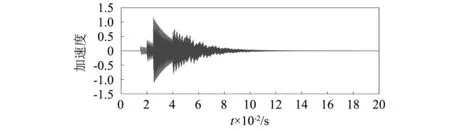
(a)仿真信号

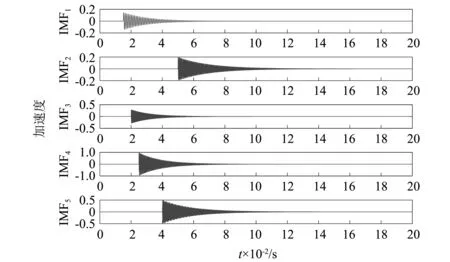
(b)仿真信号各成分分量图1 仿真信号Fig.1 Simulation signal

分别采用EMD和VMD对理论仿真信号进行分解，如图2所示。对比图1(b)和图2(a)可以发现，VMD将理论仿真信号分解为5个IMF，并且每个IMF和信号的原始分量基本一致，包括振动信号幅值和振动时刻起始点等信息，相当准确的将信号中所包含的振动事件信息有效的提取了出来。而图2(b)中，EMD分解得到了13个IMF，不但增加了迭代次数还出现了虚假模态，不利于特征信号分量的提取。因此，VMD对于处理瞬态非周期性的振动信号具有良好的分解特性。

2 样本熵

样本熵(Sample Entropy, SpEn)是由Richman和Moorman提出的一种新的时间序列复杂性的度量方法，Richman等[22]中对其详细计算过程进行了解释说明。

样本熵是对近似熵(Approximate Entropy, ApEn)算法的改进，旨在解决近似熵自身匹配引起偏差的问题。相对于近似熵而言，样本熵是条件概率的严格自然对数，因此它的计算不依赖数据长度，与已知的随机部分有更加紧密的一致性，样本熵是一种与现在的近似熵类似但精度更好的方法。

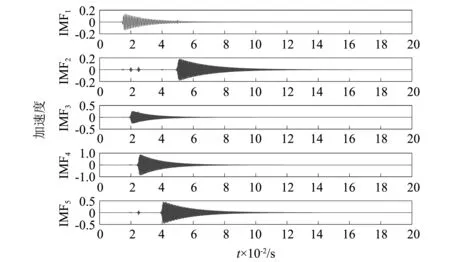
(a) VMD分解分量

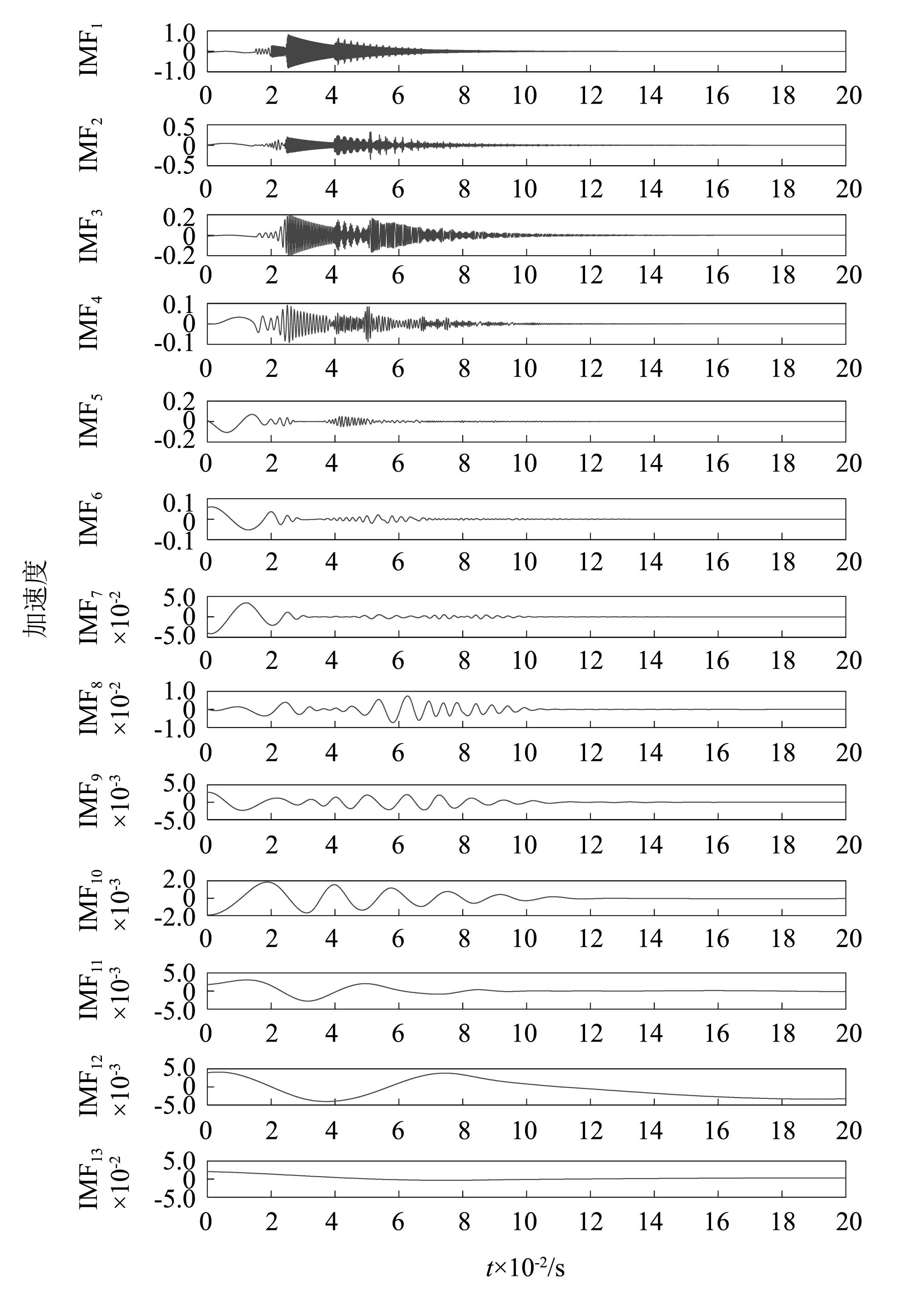
(b) EMD分解分量图2 VMD和EMD分解结果对比Fig.2 Comparison between the results of VMD and EMD decomposition

3 基于VMD和样本熵特征提取及分类

针对断路器振动信号具有冲击性、非平稳的特点，本文提出了一种基于VMD和样本熵的故障诊断方法，首先将滤波后振动信号经VMD分解成多个固有模态函数，对分解得到的固有模态函数分别求取其样本熵，完成断路器故障特征的表达，构造断路器故障特征向量；将断路器故障特征向量输入SVM进行训练，将待测样本输入训练好的SVM，完成断路器的故障识别。故障诊断流程图，如图3所示。

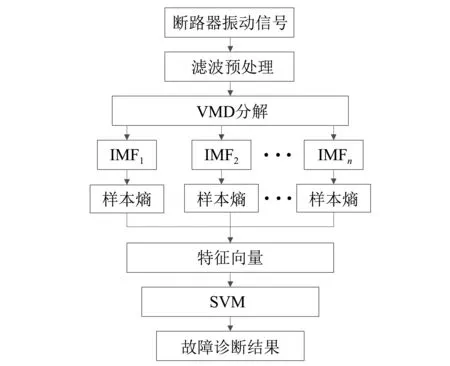
图3 故障诊断流程图Fig.3 Flowchart of fault diagnosis

4 实验应用分析

4.1 实验模拟

本文以某开关厂35 kV户外高压SF6断路器为实验对象，采用江苏东华测试公司的DH131E型加速度传感器，该传感器量程为0～5 000 m/s2。经过实验研究，将传感器安装在断路器操作机构基座上能更好地获取操作机构的振动信号。在断路器无载的情况下，除了松动基座螺丝模拟传统的基座螺丝松动故障外，还对分闸弹簧力减小与缓冲弹簧无效两种新的故障进行了实验模拟，具体做法是摘除缓冲弹簧模拟缓冲弹簧无效故障。调节分闸弹簧张紧力模拟分闸弹簧力减小故障，故障模拟，如图4所示。

图4 故障模式模拟试验Fig.4 Simulative experiments of fault patterns

为了保证采集信号的可对比性，以合闸线圈电压信号作为触发源，因断路器控制电路和实验设备处理速度问题，实验中发现在采集到触发信号时已有振动发生，故设置了负延时采集。在正常状态下和三种故障状态下分别操作20次，设置采样频率为10 kHz，数据采集器在断路器动作时采集6 000点，共得到80组数据。操作机构运动过程中典型振动信号如图5所示。从图5中可以看出，在时域内观察四种状态下断路器振动信号没有明显的差异与变化规律，因此需采取合适的方法从差异较小的振动信号中提取故障特征参数进而对其进行状态识别与分类。

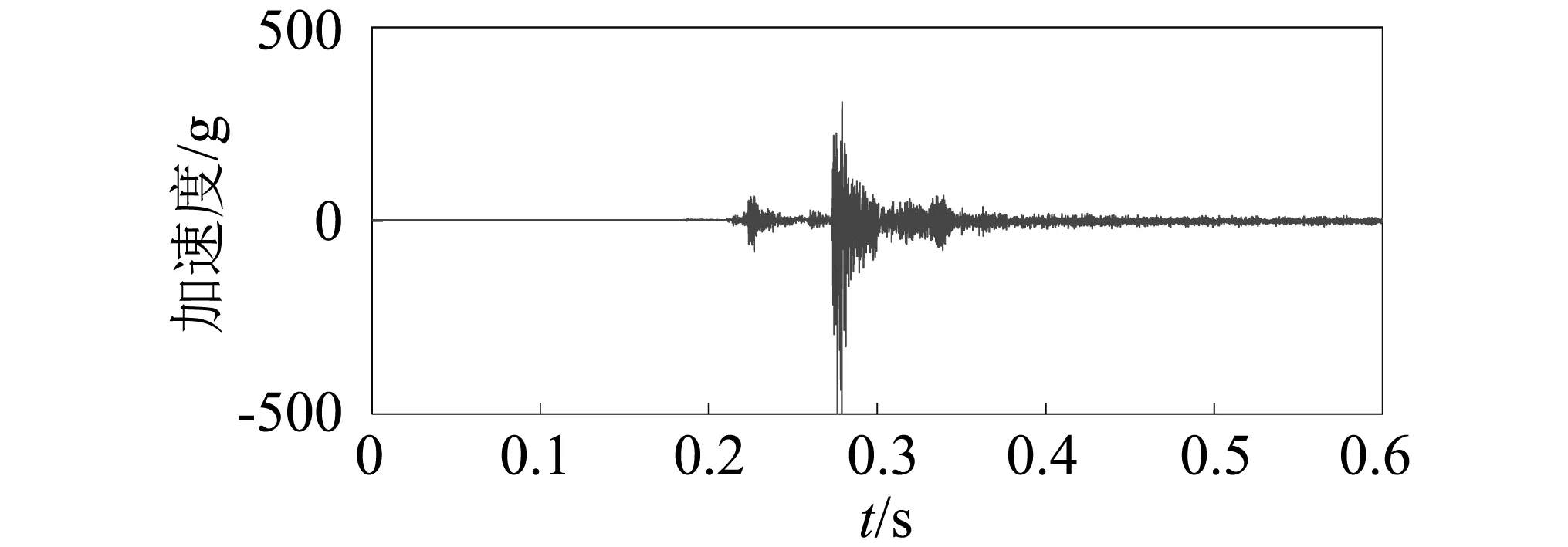
(a)正常状态

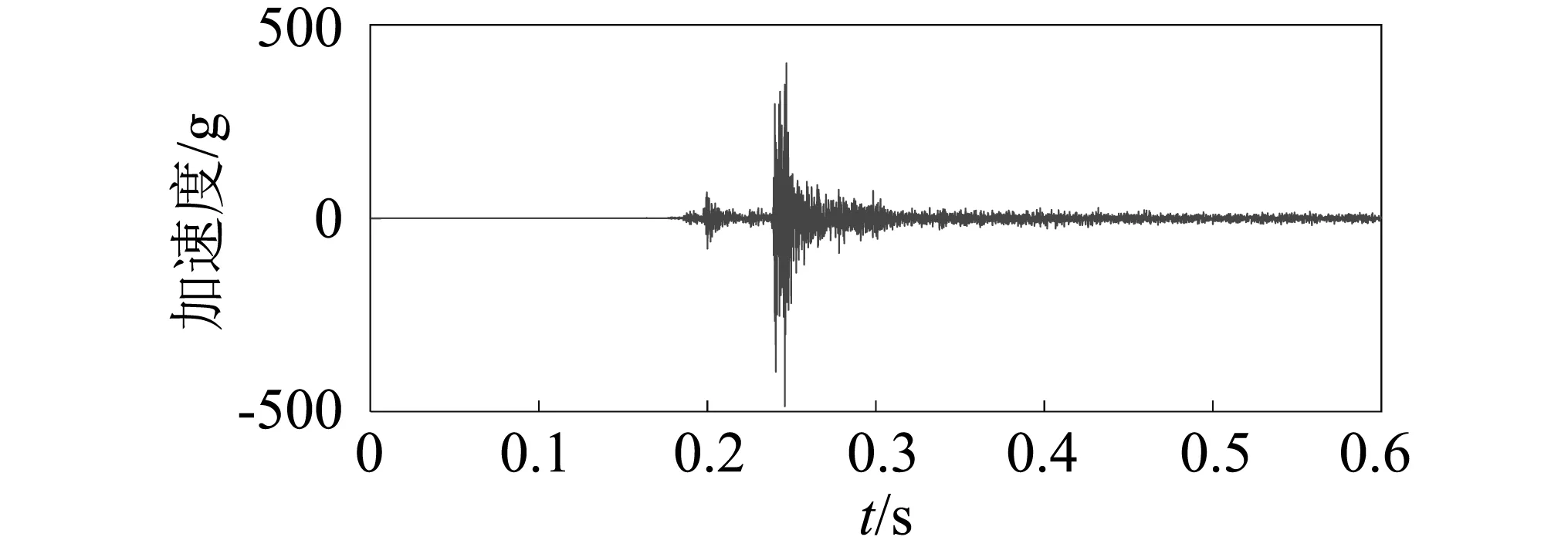
(b)分闸弹簧力减小

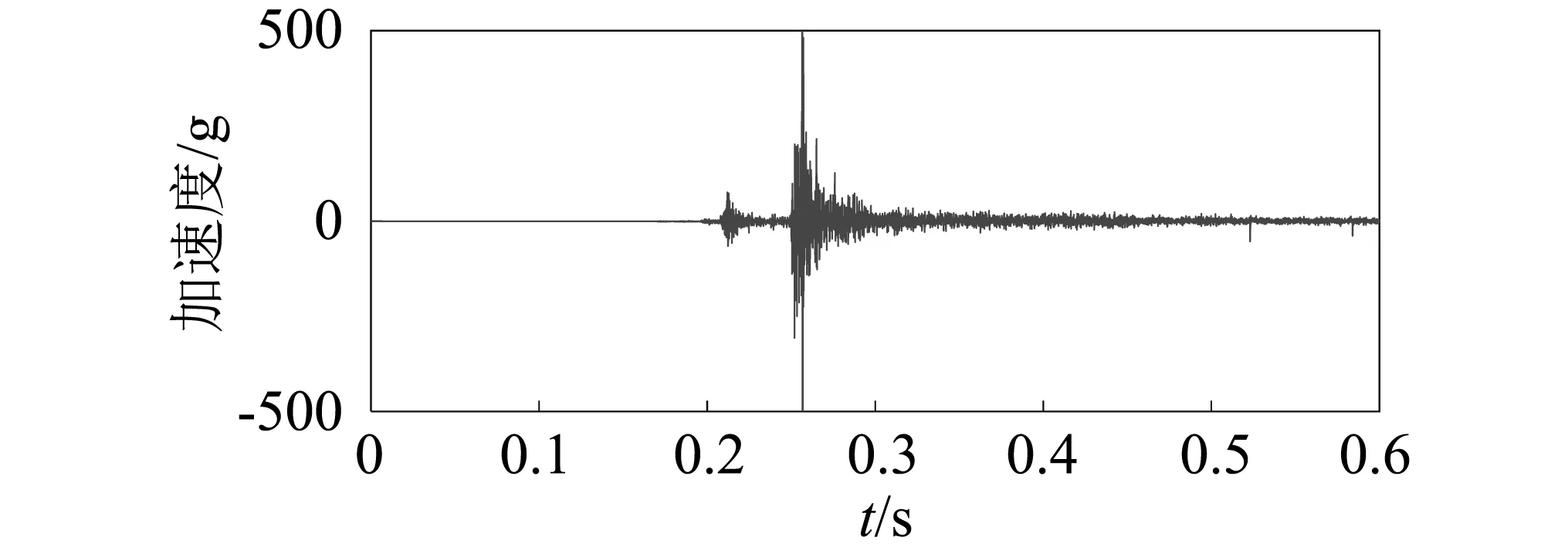
(c)基座螺丝松动

(d)缓冲弹簧无效图5 高压断路器振动信号Fig.5 Vibration signal of high voltage circuit breaker

4.2 特征参数提取

首先对采集数据进行默认阈值去噪处理，得到去噪后重构的振动信号；后对各组去噪后的信号进行VMD分解，对分解得到的固有模态函数分别求取其样本熵，完成断路器故障特征的表达，构造断路器故障特征向量。本次实验以前56组数据作为训练集，后24组实验作为测试集。部分训练集样本熵如表2所示，表中状态标签1、2、3、4分别代表断路器正常状态、分闸弹簧力减小、基座螺丝松动、缓冲弹簧无效。

4.3 模式识别与分类

断路器本身的工作特性决定了断路器不能频繁地操作，实际实验采集的测试数据量有限，测试样本数较少不利于故障识别训练。传统使用的神经网络方法需要大量的测试样本，样本越多，最终识别越准确。支持向量机却是一种基于小样本训练的识别方法[23]，更适合于断路器故障识别与分类。这里使用开放源码的支持向量机工具libsvm 3.21最新版，分类采用“一对其余”策略，将正常状态下的样本与其余故障状态样本组合成4种状态，训练时依次把某个类别的样本归为一类，其他剩余的样本归为另一类，这样4个类别的样本就构造出了4个SVM，每个SVM分别将某一类别从其它类识别出来，最终形成四组“一对三”的两类分类器。这种方法只需要训练4个SVM，分类函数较少，分类速度相对较快。

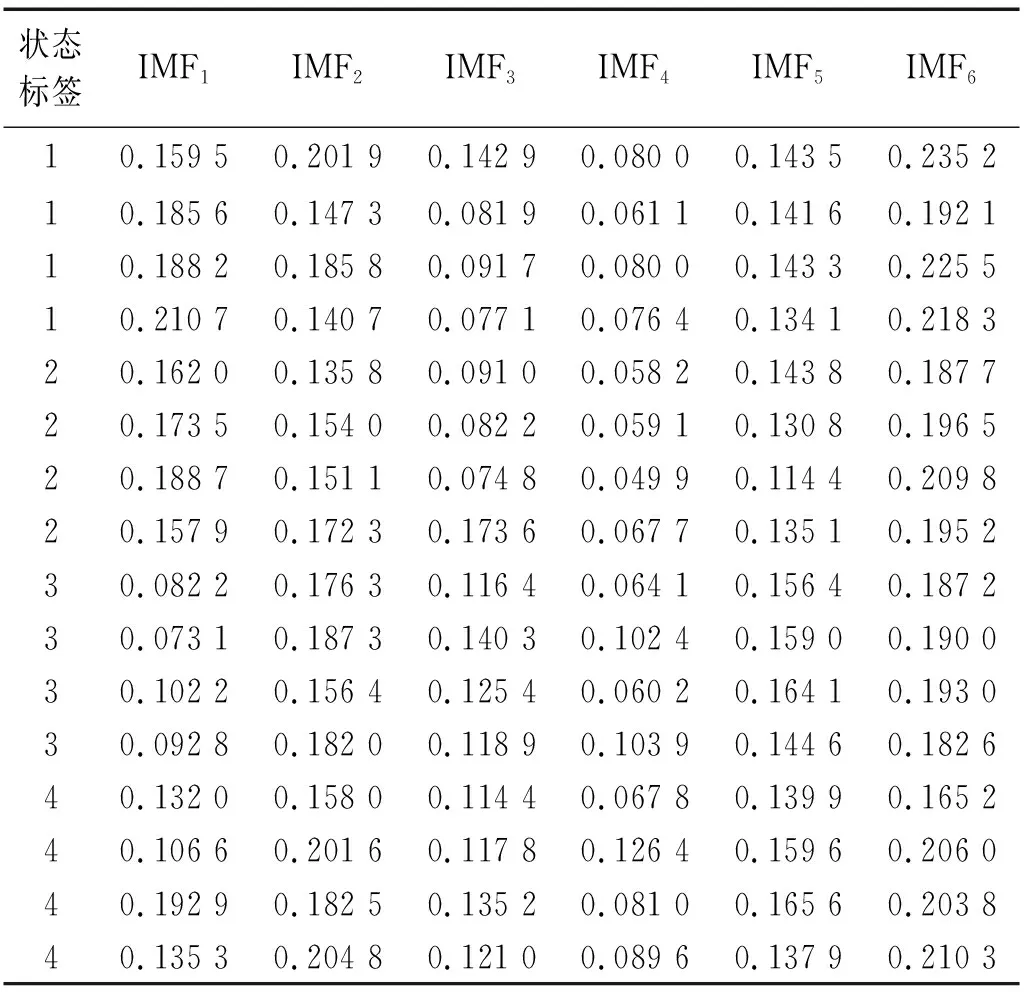
表2 训练集样本熵Tab.2 Sample entropy of training set

支持向量机最重要的一个参数就是核函数，考虑到径向基函数模型简单。参数少，选择径向基函数作为核函数，在此核函数下，用训练集样本训练支持向量机，然后使用训练好的支持向量机对测试集样本进行分类测试，测试集总共24组数据，每种状态6组数据，与训练集数据不重叠。部分测试集样本熵如表3所示，测试结果，如图6所示。

图6 实际分类与预测分类对比图Fig.6 Comparison chart of actual classification and prediction classification

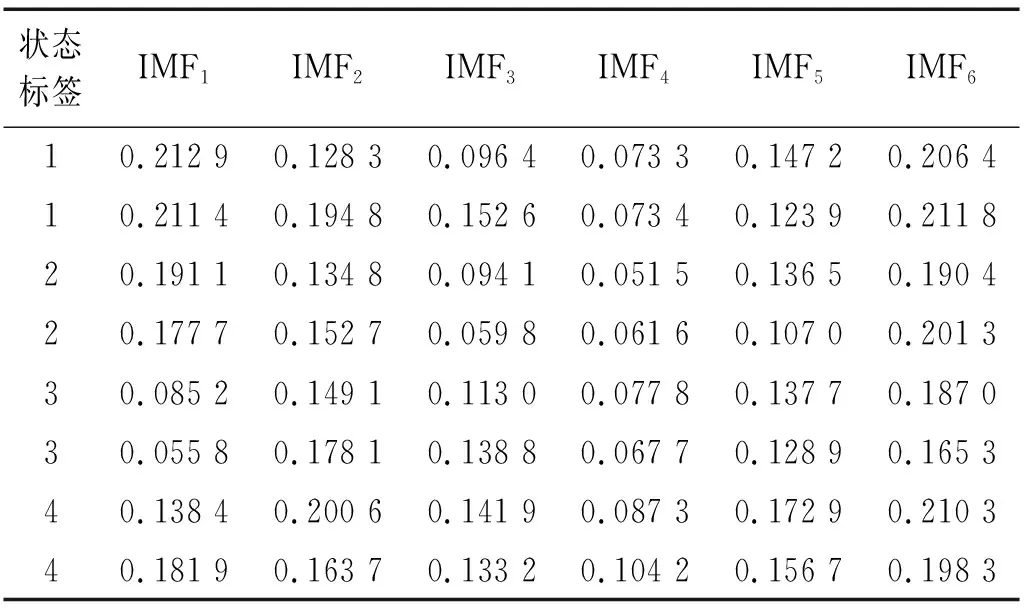
表3 测试集样本熵Tab.3 Sample entropy of test set

从图6中可以看出，测试集中24组数据分类结果与实际类别一致，说明利用测试好的SVM对测试样本进行分类测试，测试结果全部分类正确。

为了对比验证，利用EMD对振动信号进行分解，并计算分解得到模态的样本熵值；利用VMD对振动信号进行分解，计算分解得到模态的样本熵值、近似熵值和模糊熵值；与此同时计算信号本身的样本熵值，分别以VMD样本熵(VMD-SpEn)、VMD近似熵(VMD-ApEn)、VMD模糊熵(VMD-FuEn)、EMD样本熵(EMD-SpEn)和信号本身SpEn五种方法作为断路器故障状态的特征向量，对SVM进行训练和分类测试，表4为不同故障特征提取方法识别率比较结果。

表4 不同故障特征提取方法识别率比较Tab.4 comparison of classification in different feature extraction methods

由表4可知，基于VMD-SpEn方法得到的特征向量的正确识别率高于EMD-SpEn和信号本身的SpEn方法得到的特征向量的正确识别率?这是因为相对于其他分解算法，VMD具有更好的鲁棒性，能有效的提取出具有不同中心频率的模态成分，具有良好的分解特性。与此同时，基于VMD-SpEn方法得到的特征向量的正确识别率高于基于VMD-ApEn和VMD-FuEn方法的识别率，说明样本熵具有良好的特征提取能力，组成的特征向量差异明显，故具有更高的状态识别率。

该结果表明采用VMD分解。样本熵特征值提取。网格参数优化和支持向量机分类在内的信号处理和诊断方法应用在断路器振动信号分析中，能够准确地实现断路器故障试验中各种状态的分类。

5 结 论

为了识别高压断路器的故障类型，本文首次采用变分模态分解法对断路器振动信号进行分解，并从理论角度验证了其分解的优越性；然后计算各IMF样本熵作为特征向量，并以此作为SVM的输入向量进行分类训练；最后将测试样本信号故障特征输入训练好的SVM，在SVM核函数参数进行网格算法优化的基础上进行状态识别及分类。研究得出以下结论:

(1)将VMD和样本熵相结合的方法首次应用在高压断路器振动信号的分析中。利用VMD良好的噪声鲁棒与样本熵相结合，有效提取出了断路器在不同运行状态下的特征向量。

(2)对于断路器测得振动信号，采用VMD分解得到的各模态样本熵作为特征向量，与其它方法得到的特征向量相比，有更高的故障类型识别正确率。

(3)实验结果表明，本文算法能快速有效地提取断路器故障振动信号的特征向量并能正确地进行状态识别和分类，提高了分类精度，获得了较好的诊断效果，为断路器故障诊断技术提供了较为实用的解决方案。