一类高阶拟线性波动方程整体解的指数衰减

叶子青，叶耀军

(浙江科技学院 理学院，杭州 310023)

引 言

本文研究以下高阶拟线性波动方程的初边值问题：

(1)

u(x,0)=u0(x)，ut(x,0)=u1(x)，x∈Ω，

(2)

(3)

当m=a=1，b=0时，式(1)是具有耗散项的非线性波方程，许多人用不同的方法和技巧对此类方程的Cauchy问题或初边值问题进行了研究，得到了整体解的存在唯一性及衰减估计，并建立了解的爆破性质，如文献[1-4]。在a,b>0的情况下，Ikehata[5]证明了如果初值{u0,u1}属于稳定集，并且足够小，则式(1)～(3)存在整体强解。

当m>1,a,b>0时，式(1)具有明确的物理背景，它描述了受Kelvin-Voig型内部材料阻尼项和线性阻尼项μut影响的Woinowsky-Krieger型振动梁模型[6-7]。若a=0,b>0，Li[8]和Ye[9]研究了带有非线性耗散项的式(1)的初边值问题，并得到了如下结果：r>2时解整体存在；r<2时对于任意的负初始能量，解在有限时间内发生爆破。之后，Messaoudi等[10]改进了文献[8]中的结论，并且证明了当初始能量有上界时与文献[8]有相同的结果。同时，Galaktionov等[11]证明了μ=0时，式(1)的Cauchy问题整体解的存在性和不存在性。然而，他们的处理方法不能应用于式(1)～(3)。文献[12-15]研究了更广泛的Kirchhoff型方程及方程组的初边值问题，证明了其局部解和整体解的存在性与不存在性，并建立了整体解的长时间行为。

1 预备知识

定义式(1)～(3)解的能量如下：

(4)

初始总能量为

引理3令u(t)是式(1)～(3)的解，则t>0时，E(t)是非增函数，且

E′(t)=-μ||ut||2≤0。

(5)

证明：在式(1)的两边同乘以ut，并在Ω×[0,t]上积分，由分部积分得

(6)

由此可知，E(t)是可积函数的原函数，故对于任一正则解u(t)，能量E(t)关于t绝对连续且满足式(5)。因此，由稠密性原理知，结论成立。

定理1～2给出式(1)～(3)局部解和整体解的存在性结果，其证明过程参见文献[5]。

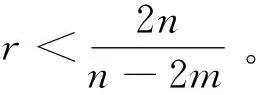
此外，下式成立

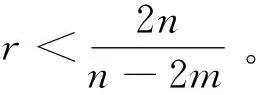
2 指数衰减估计

引理4对研究式(1)～(3)整体解的指数衰减估计起着重要的作用。

引理4[18]令F:R+→R+是非增函数，并假设存在常数L>0使得

本文主要结果叙述如下。

定理3在定理2的假设条件下，式(1)～(3)的整体解有如下指数衰减估计：

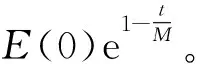
式中M>0是常数。

证明：令E(t)=E(u(t))，如果能够证明整体解的能量满足下列估计

则由引理4可得定理3的结果。

(7)

(8)

由式(8)知

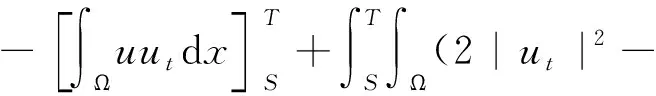
(9)

根据式(4)、式(7)和式(9)得

(10)

由式(4)和式(7)知E(t)>0。联合引理1，式(4)和Cauchy-Schwarz不等式有

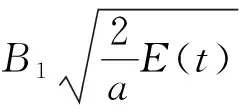
(11)

应用式(11)和引理3有

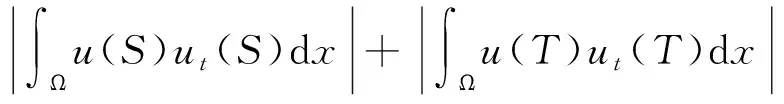
(12)

由式(10)和式(12)得

(13)

从式(4)、式(5)和引理2可推出

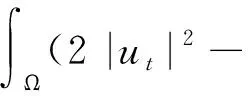
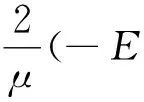
(14)

因此，由式(14)知

(15)

由式(13)和式(15)得

(16)

选取ε足够小使得ε<2，则由式(16)知

(17)

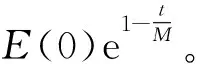
定理3证毕。

3 结 论

本文研究了式(1)的初边值问题，在式(1)～(3)解的局部存在(定理1)和整体存在(定理2)的前提条件下，应用Komornik的积分不等式(引理4)、Cauchy-Schwarz不等式及能量估计方法，得到了式(1)～(3)的整体解能量的指数衰减估计(定理3)。