基于分位数回归模型的债务违约损失预测

吴建华 张颖 王新军

(1.济南大学数学科学学院，山东 济南 250022；2.山东大学经济学院，山东 济南 250100)

引言与文献综述

随着我国宏观经济低位运行和供给侧结构性改革步入深水区，各个行业企业被迫转型发展，这导致了国内商业银行不良资产余额和不良率持续上升。公开数据1显示，截至2017年第一季度，国内商业银行不良贷款规模约1.58万亿元，不良贷款率为1.74%，不良贷款规模保持稳步上升趋势。分机构看，我国各类银行机构的不良贷款余额的绝对数在不断增加，农村商业银行不良贷款率在五类机构中最高，截至一季度为2.55%，然而同期的外资银行不良率则明显较低为0.89%。以上数据表明相比外资银行，国内商业银行在信用风险量化和控制能力方面有待进一步提高。在这种背景下，研究银行贷款的违约损失率及其影响因素，对进一步防范出现和处置不良贷款有重要的现实意义。根据Basel II/III对信用风险的经济资本的要求，实施内部评级高级法的商业银行需违约概率和违约损失率等重要的参数。中国银监会也于2012年6月在Basel Ⅲ的基础上公布了《商业银行资本管理办法(试行)》，办法规定采用内部评级法计量信用风险加权资产的商业银行需要估计违约概率(PD)、违约损失率(LGD)、违约风险暴露(EAD)、相关性(Cor)和有效期限(M)。其中最关键也是最难估计的两个参数就是PD和LGD。实际上，除了资本监管要求之外，PD和LGD的准确预测也是商业银行进行贷款风险调整定价、经济资本计算和资产支持证券或者信用衍生品定价的基础。

然而，从早期的相关研究来看，学界主要关注违约概率PD的估计，较少关注违约损失LGD的估计，随着2004年Basel II协议的推出，学界和业界对于LGD的研究开始大量增长。从理论研究层面来看，国外对LGD的研究最早始于1990s年代中期，随后陆续出现了一些关于LGD的理论和实证的研究。从现有的研究来看，基本思路主要是采用某种统计方法分析LGD的影响因素和对LGD进行拟合和预测。

在分析LGD的影响因素方面，比如Hibbeln and Gürtler(2011)[5]等研究发现，债务结构(抵押/保证及清偿优先级别)、债务人的信用质量或者违约概率、清偿过程、债务人所属行业和宏观经济状况对LGD的影响较为显著，但对于企业规模、贷款规模和贷款期限等因素对LGD的影响的结论并不一致。国内的相关研究可以参考陈光忠等(2010)[15]、曹萍(2015)[14]和吴建华等(2016)[18]等代表性文献。

从LGD拟合和预测中所采用的统计学方法来看，由于LGD数据具有典型的非正态性和双峰的U型分布，而标准的线性回归无法有效的对LGD拟合和预测，为此需要利用其他的回归技术进行处理。Cribarineto(2004)[4]利用了贝塔分布拟合LGD的分布，它不需要正态性假设和同方差假设，所以适用范围广泛。Bellotti and Crook(2007)[1]利用比例响应回归FRR对LGD进行拟合。Yashkir and Yashkir(2013)[13]对比研究了几个最为流行的LGD模型(LSM，Tobit，三层Tobit，贝塔回归，膨胀贝塔回归，截断伽马回归)的预测绩效。最近陈暮紫等(2015)[16]基于预期效用分布理论框架下，构建了违约回收率的贝塔分布修正模型。

纵观以上已有的LGD研究，无论是采用参数方法还是采用非参数方法，本文发现其中的分析基本结果大都是对LGD的均值预测，要么直接进行均值回归，要么最终的结果以均值的形式体现。众所周知，均值只是对概率分布的基本特征的描述，它无法刻画完整的概率分布，尤其是对于LGD的非正态、偏斜和双峰分布特征来说，问题更严重。然而，无论是从资本监管要求和信用风险量化，还是从各种信用产品的定价来看，都需要对LGD的完整分布的估计和预测。

实际上，在统计学理论研究的领域，针对均值回归不能完整描述响应变量的分布这一缺点，Koenker and Bassett(1978)[7]提出了分位数回归(QR)模型。自从分位数回归被提出以来，分位数回归得到了大量的研究，并获得了广泛的应用，其应用领域包括医学、环境科学、生物学、经济和金融领域等。特别是在金融风险量化研究中，分位数回归被广泛用于估计市场风险中的在险价值，比如Wong and Ting(2016)[12]等将分位数回归技术应用于市场风险中的各种在险价值模型，发现分位数回归具有显著的优势。

不过，以上这些研究大都集中于利用QR来量化市场风险。在信用风险量化中，尤其是在LGD估计中运用QR的研究非常少，比如Sopitpongstorn et al.(2016)[10]提出了利用非参数分位数回归和部分线性附加分位数回归来模型化平均违约回收率RR的思路。然而，从国内的相关研究来看，在这方面的研究几乎是个空白。

不同于以上的研究，本文不是利用QR估计最终的平均LGD，而是直接模型化LGD的整个分布。基于不同的分位数，区分了协变量对极低、适中和极高LGD的影响。利用HMI和HWMI两个指标来进行模型对比，然后通过样本内和样本外的对比分析以评估LGD的整个分布的拟合性。这样，本文就从一个全新的视角量化了协变量对LGD的全面的影响。

本文首先简要介绍分位数回归方法，通过模拟试验验证分位数回归刻画具有非正态、偏斜和双峰分布的适用性。然后，对实证分析的数据进行描述统计，并根据分位数回归模型实证分析的结果，对比其他几个不同模型的样本内和样本外的预测绩效，最后得出结论。

模型构建及其估计

根据上述文献综述可知，LGD具有非正态性、极端偏斜和双峰U型分布的特征，而且在信用风险资本监管中计算非预期损失时，需要完整的损失分布。而现有的关于LGD的估计的方法中大都是均值回归，均值只能刻画分布的平均特征，而不能完整的描述LGD的分布，尤其是对于LGD的具有U型分布设定来说问题更严重。本文试图利用分位数回归解决以上的问题。

一、分位数回归模型

下面首先给出分位数回归的简要概述，然后通过随机模拟验证分位数回归在刻画非正态、极端偏斜和双峰分布设定中的适用性。

沿用Koenker(2005)[7]提出的分位数回归思路，假设随机变量Y的分布函数为

Y的第τ分位数的定义为满足F(y)≥τ的最小的y值，即

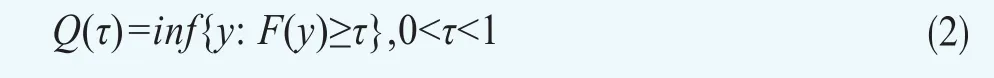
回归分析的基本思想是使样本值与拟合值之间的距离最短，那么样本分位数回归就是使加权误差绝对值之和最小。具体来说，对于Y的一组样本{y1,…,yn}，需要求出满足下式的ξ

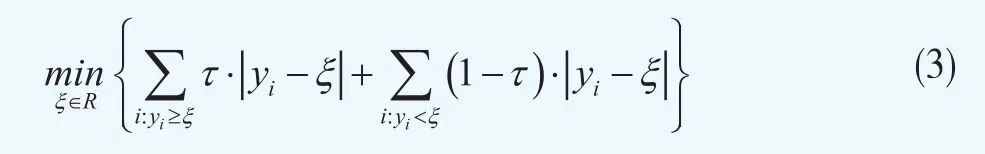
其中τ为分位数权重，ξ为目标拟合值。上式可以等价的表示为：

其中，ρτ(u)=(τ-I(u＜0))u，I(z)为指示函数，z是条件关系式，当z为真时，I(z)=1；当z为假时，I(z)=0。以上基于Y的一组样本{y1,…,yn}，估计ξ的过程就被称为是分位数回归。

假设因变量Y可以由k个自变量组成的矩阵X线性表示。

其中误差u满足非自相关假设。设(X,Y)的一组随机样本为{(x1, y1),…,(xn ,yn)}，那么，Y的第τ分位数的样本条件分位数函数为

其中x，βτ都是k×1阶列向量。那么，估计Y的第τ分位数回归方程系数βτ的方法是，使得下面的目标函数或者说加权误差绝对值之和最小的系数，即

以上基于(X,Y)的一组样本{(x1, y1),…,(xn ,yn)}估计βτ的过程被称为是条件分位数回归。为了表达的方便，在不引起歧义的情况下，本文不区分“分位数回归”和“条件分位数回归”，而是统一称为分位数回归。

由于目标函数(7)是不可微的，传统的对目标函数求导的方法不再适用，因此需要采用线性规划方法来估计分位数回归方程参数比如单纯形算法、内点算法和平滑算法等。许多常见的计量经济和统计软件都可以实现对分位数回归模型的估计和假设检验。本文在分位数回归模型分析中主要采用统计软件R语言进行处理。

二、分位数回归在LGD量化中的适用性分析

值得一提的是，在分位数回归模型设定中，对于误差u来说，除了非自相关假设外，没有更多的模型假设，因此可以处理较高水平的误差异质性。相对于最小二乘法，加权最小绝对离差和法的假设条件更为宽松。显然，对于LGD分布的非正态性、偏斜和双峰特征，都可以利用分位数回归容易处理。

下面通过数值模拟试验检验分位数回归QR在处理LGD分布的非正态性、偏斜和双峰特征方面的适用性。

为了生成LGD分布所具有的非正态、偏斜和双峰特征，给定如下的数据生成过程，yi=β1τi+β2τixi+ui，其中自变量xi来自N(0,0.01)中的随机抽样，为了模拟数据的双峰特征，令β1τi=zτi，β2τi=zτi－0.5，zτi=B(0.2)，设误差项u是高斯分布，即u～N(0,0.04)。重复以上的模拟过程5000次，可以得到5000模拟个样本点。图1给出了模拟的结果的散点图和直方图。

下面利用QR估计数据生成模型的参数。图2给出了模拟数据的QR参数估计，同时也给出了OLS估计作为对比，其中的置信区间是基于95%的置信水平给出的。

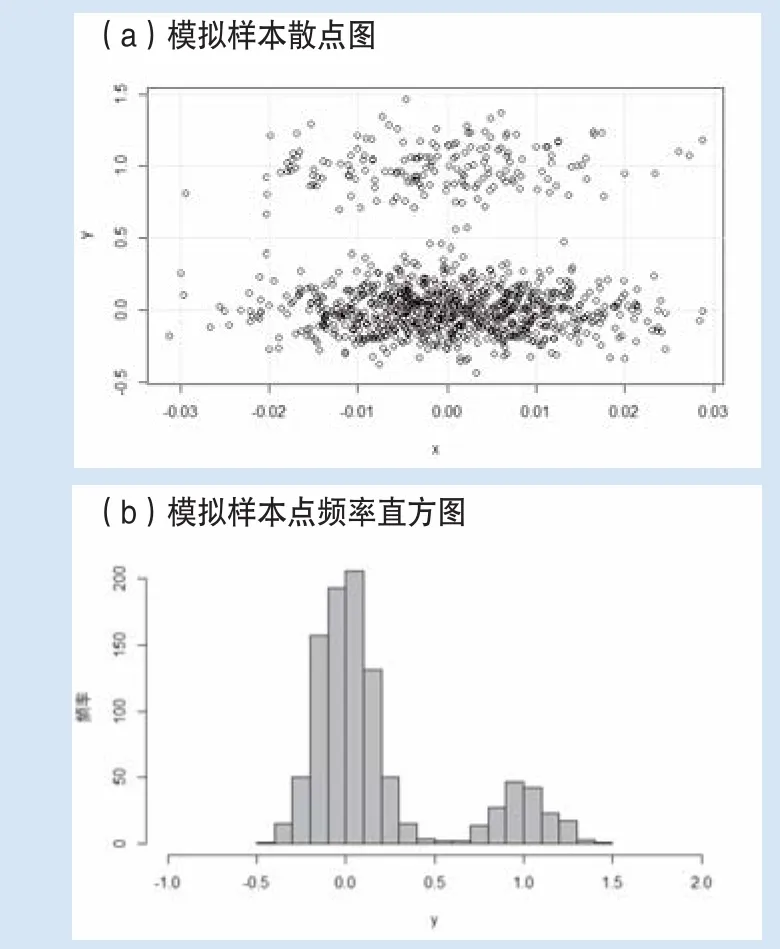
图1 模拟数据

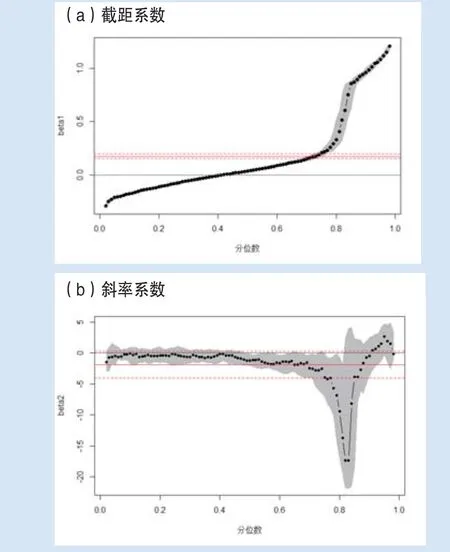
图2 模拟数据的参数估计

从图2中可以看出，对于截距项和斜率系数来说，普通最小二乘估计估计给出了常数估计，而分位数给出的截距项和斜率系数估计是变动的，它随着不同的分位数而变化，它全面的反应了随机变动的截距和偏斜的信息。显然，普通最小二乘估计既不能捕获非常数的截距项，也不能捕获协变量的显著的作用。这会导致对截距项和斜率的错误估计。相反，分位数能够捕获较低和较高分位数的差异。对于水平和正态分布误差项来说，截距项包含了两个显著不同的取值。我们所估计得到的斜率，是具有可变影响的统计显著的协方差。

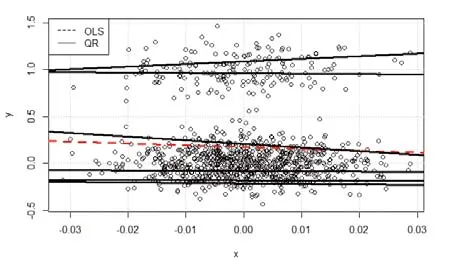
图3 OLS和QR的样本内预测

对于数据生成过程来说，图3展示了基于5000个独立模拟的观测值的分位数回归(实线)和普通最小二乘估计(虚线)的样本内预测直线，显然，从图3可知，普通最小二乘法回归只能生成一条拟合曲线，显然完全不能拟合具有双峰特征的数据，而分位数回归用多条分位数直线，能够更好的拟合双峰数据。

综上所述，上面的模拟试验表明，对于非正态，偏斜和双峰特征的数据来说，分位数回归可以有效的进行参数估计和拟合。实际上，由于不同分位数下的回归系数估计量通常是不同的，即解释变量对不同水平被解释变量的影响不同，所以分位数回归能够更加全面的描述被解释变量条件分布的全貌。而且与最小二乘估计相比，“加权最小绝对离差和法”的估计结果对离群值则表现的更加稳健。此外，分位数回归对误差项没有很强的假设，因此分位数回归估计更适合于估计非正态分布假设下的模型。显然，对于LGD分布的非正态性、偏斜和双峰特征，都可以利用分位数回归容易处理。

三、分位数回归估计的检验方法选择

传统的LGD模型和校验方法重点关注均值的预测。已有的文献中使用了标准的可决系数R2和平均绝对值MAE或者根均方误差RMSE。这些测度指标侧重于检验依赖变量的均值的绩效，而无法捕获依赖变量的完整分布的行为。为此，在评估整个分布的拟合度时，我们采用了其他的测度。沿用Wagenvoort(2006)[11]的思路，下面给出Harmonic Mass Index(HMI)和Harmonic Weighted Mass Index(HWMI)两个指标作为均值绝对和均值平方差，如下：

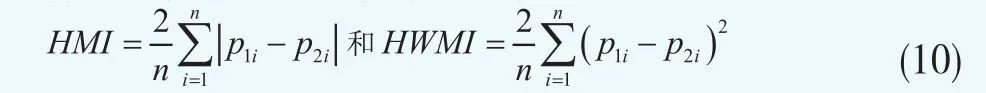
另一个绩效测度指标是Kolmogorov-Smirnov (KS)检验，原假设是数据服从回归方法对应的被估计的分布。检验统计量D、关键值c和显著性水平α，如下给出

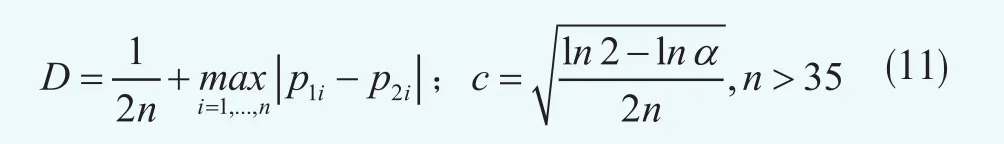
KS的取值越高，表明拟合效果越差。KS检验校验了最大偏差，但是不是整个的拟合优度。结果应该被谨慎的对待。

在后面的估计检验中，我们将利用拟合优度R2、HMI、HWMI和KS这四个测度指标，从样本内和样本外两个角度，对比QR与其他的4个模型。

实证结果与分析

一、变量筛选与样本数据的处理

本文所使用的数据为山东省某城市商业银行在2009年7月～2015年8月处置完毕的全部不良贷款数据。针对可能存在的数据异常点问题，参照Betz et al.(2016)[2]提出的选择准则以确保数据的一致性。考虑了所有的现金流之和为未结清的违约暴露的90～110%之间的贷款，贷款的支付为未结清的处理暴露的-10%到120%之间。通过对数据进行筛选和清洗，最终得到信息比较完整的贷款7155笔及其违约之后2年的清收处置资料。数据指标包括：贷款期限、信用评级、保证、抵押和企业所属行业。在债务追偿方面，通过数据实录，获得了债务违约时间、核销金额、追偿金额、追偿持续时间、追偿成本等。其中追偿成本包括基本追偿费用(短信、电话和信函等方式)和专项追偿费用(登门追偿、司法追偿、处理抵押物等方式)。有关违约暴露及追偿费用的描述统计如表1所示。

本文采用银行业实践中常用的清收违约损失率公式计算实际发生的LGD，计算公式如下∶

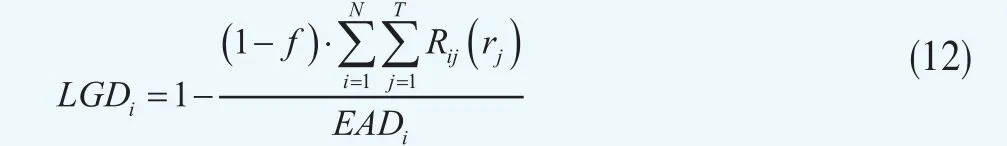
其中，f为衡量单位回收金额所支付的费用，Rij(r)为第i笔贷款以贴现率rj计算的第j期贷款回收额的现值，EADi为为第i笔违约贷款的风险暴露(包括违约贷款余额和欠息金额)，N为贷款的总笔数，T为自违约起直到清偿终结时的时间跨度。

显然，实际LGD计算中的一个困难是清收过程中形成的各种成本f的确定。比如与特定资产相联系的各种抵押品的评估费用等，在贷款清收过程中需要支付的清偿部门的各种管理费用等。此外，在我国银行业实践当中，不良贷款的清收往往需要多个部门相互协调才能完成，这就加大了成本核算和分摊的难度，造成难以测算回收违约债项的直接与间接成本。本文对相关清收费用进行了实际统计，并以此为基础测算了单位回收金额所花费的平均成本作为f的代替。

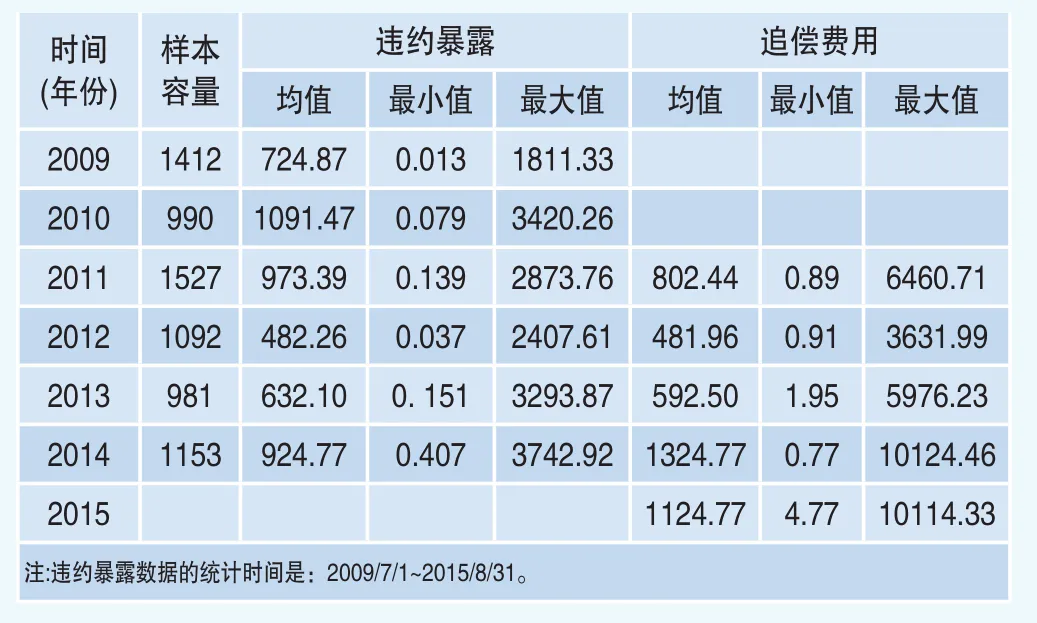
表1 违约暴露及追偿费用的描述统计 (单位：万元)

对于回收金额Rij的构成。本文使用贷款余额差额法来确定主要回收金额，即计算违约时点与T年后相同时点贷款余额之差作为现金回收部分，再加上以物抵债、债务转移回收部分，并减去新发放贷款部分。

对于贴现率rj的设定。采用在回收期限上与违约贷款相对应的贷款利率作为贴现率比较合理。因此在后面的实证分析中，本文采用中国人民银行公布的不同期限的贷款基准利率作为相应的贴现率。

对于的贷款的清偿持续时间T的设定。根据贷款回收的历年数据统计分析确定清偿持续时间T的取值是一个比较合理的方法。本文利用获取的贷款回收的历年数据统计分析可知，贷款回收额在违约后1年内占全部回收额的65%，2年内占比达到83%，第三年仅占8%，因此，将违约后2年作为清收的终结时间是一个较好的近似。

通过(9)式，我们可以计算得到所有的7155笔贷款的实际LGD。图4给出了最终LGD数据的频率分布直方图。

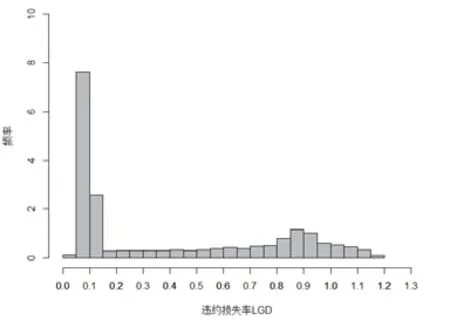
图4 实际LGD的分布

从图4可以看出，大多数LGD几乎分布在0和1的附近。整体上看，它具有双峰特征，违约损失率较低(5%左右)或违约损失率较高(90%左右)的债项较多，大多数违约损失率较低的债项位于这两者之间。从两个典型的位置统计指标来看，均值为0.41，中位数为0.11，即LGD是高度偏斜的。显然，大多数标准的统计回归方法都不能充分的捕获双峰和偏斜的特征分布的这些性质，因此本文尝试利用分位数回归来处理这些数据。另外，值得一提的是，本文结果与杨军等(2009)[29]和陈荣达等(2014)[26]的研究结果有某些相似之处，这表明，国内商业银行LGD分布大都是近似的“U”型分布。不过值得一提的是，本文测算的实际LGD的最大值超过了1，这说明，在债务清收过程中所存在的各种管理成本、法律成本、清算费用或者手续费和佣金以及较高的担保回收成本是不能忽略的。

已有的研究文献表明影响LGD的因素大致包括三类：债务人因素、债项因素和宏观经济因素。对于债务人来说，所处的行业和信用等级等因素会直接影响后期的债务偿还。从债项因素来看，期限、担保和逾期时间对后期的违约损失都具有显著的影响。此外，逾期时间显然会直接影响到债务回收的结果，追偿过程持续的时间越长，债务的LGD越大。

结合以上的讨论，选择了七类指标：违约暴露、贷款期限、信用、担保、抵押、行业和宏观金融变量作为分位数回归中的协变量。表2给出了五个分类变量的实际LGD的均值和分位数以及相应的样本容量。

在表2中，我们根据贷款是否在1年以内，区分了短期和其他期限，相比短期债项，其他期限的债项隐含着更高的LGD。例如，短期项的实际平均LGD是0.22，而其他期限的债项的实际LGD的均值为0.34。高级的债项对于损失起着重要的作用。平均来说，AAA级信用贷款的LGD为0.17，A,AA级信用贷款的LGD为0.27，而其他级别的信用贷款的LGD为0.51。我们也区分了有无保证的贷款，即是否对贷款有额外的保证。从均值来看，对于是否有保证的贷款来说，LGD的差距较小。然而，从中位数来看，有保证的贷款为0.16，没有保证的贷款为0.07。这种反常的现象可以被解释为，虽然保证可能会降低未来的损失，但是它给出了非对称的信息问题，比如道德风险，这会导致更高的损失。此外，我们区分了城市房产抵押、非城市房产抵押、机器设备抵押和其他抵押的贷款。具有城市房产抵押和非城市房产抵押的贷款的平均LGD差距不大，分别为0.17和0.19，而机器设备抵押的贷款的平均LGD较高为0.44，其他的非实物抵押具有更高的平均LGD为0.52。对于大多数行业来说，平均LGD大都分布在0.15～0.45之间。最大值对应着农林牧渔为0.46，最小值对应着建筑行业为0.16。建筑行业较低的平均LGD也能解释目前我国商业银行的贷款很大一部分流向房地产行业的现象，商业银行更愿意把贷款发放到违约损失率较低的行业。

表2 各种变量下LGD的均值和分位数 (单位 ：%/笔)

已有的研究也表明，宏观经济和金融状况对LGD也有显著的影响。本文选择GDP的年度增长率作为宏观经济状况的代理变量。Chava et al.(2011)[3]研究发现10年和3个月的国库券收益率之间的绝对期限价差可以作为驱动LGD的显著变量。沿着这个思路，本文利用基于3个月期的国库券收益率的期限价差刻画未来金融和货币状况的预期的显著的变量。

二、实证分析结果和解释

1.参数估计结果

由于上面所分析的影响LGD因素中，除了两个宏观金融变量GDP增速和期限价差之外，其他的都是定性因素，为了在回归分析中反映这些定性因素对LGD产生的影响，本文通过设置虚拟变量来反映定性因素中所包含的信息：贷款期限(其他期限)、信用(其他级别)、保证(无保证)、抵押(无抵押)和行业(金融保险)，然后引入到分位数回归模型中。这些虚拟变量的设置规则如下：

松嫩平原是一个潜水普遍分布的大型蓄水盆地，东部高平原和西侧的大兴安岭山前倾斜平原，既是山区基岩裂隙水的排泄区，又是中部承压水盆地的主要补给区。

(1)贷款期限(其他期限)。贷款的期限会显著影响到违约以及违约损失率。期限越长违约概率越大，反之亦然。考虑到处理的方便，本文区分了短期和其他期限的两类贷款期限。本文以1年期为参照设置了虚拟变量“贷款期限”：如果期限在1年及以内，则贷款期限取值为1，否则取值为0。

(2)信用(其他级别)。对于企业来说，信用评级通常包括A类级(AAA级、AA级、A级)，B类级(BBB级、BB级、B级)，C类级(CCC级、CC级、C级)和D类级。从实际的违约状况来考虑，本文以B类级及其以下为参照，设置了两个虚拟变量“信用”：。如果贷款企业属于“AAA级”或者“A,AA级”则信用相应的取值为1，否则取值为0。

(3)保证(无保证)。根据贷款有无保证，贷款可以分为有保证贷款和无保证贷款。本文以无保证为参照，设置了一个虚拟变量“保证”：如果有房产抵押，则保证取值为1，否则取值为0。

表3 分位数回归模型和OLS的参数估计结果

(4)抵押(无抵押)。根据贷款的抵押品类型大致包括：城市房产，非城市房产，机器设备，非实物抵押和无抵押。考虑到抵押的金额的大小和处理的方便，本文以房产抵押为参照，设置了一个虚拟变量“抵押”：如果有房产抵押，则抵押取值为1，否则取值为0。

(5)行业(金融保险)。根据行业实践来看，相比其他的行业，金融保险行业是一个特殊的行业，其违约率相对较低。本文以金融保险为参照，设置了八个虚拟变量“行业”：如果行业属于农林牧渔、煤炭矿产、建筑房产、机械制造、交通通讯、批发零售、医药卫生和电力油气中的任何一个，则信用相应的取值为1，否则取值为0。

表3给出了针对以上的变量进行的第0.05, 0.25, 0.50,0.75和0.95分位数的估计结果和相应的OLS估计结果。括号中的标准误是利用核估计方法计算的。

从表3的结果可以看到，参数估计的水平和显著性依赖于各种的分位数。截距项表示了协变量为零时的LGD的演变方式。对于较低的分位数来说，截距项几乎是完全收敛到零，而且在中位数之前呈现单调递增的趋势，直到在更高的分位数上达到总损失的最大值。

在分布的左尾部分(即0.05和0.25分位数)，只有如下的较小的影响可以被观测到：短期债务影响系数为-2.3%和-2.4%。AAA级信用贷款的LGD影响较小会降低4.7～5.9个百分点。有趣的是，保证的存在会提高损失2.3到3.1个百分点，这或许是有额外的管理成本导致的，因为此时保证人会变得很积极。在中位数的情形中，该影响会更大，会上升5.7个百分点。

大多数的控制变量在中位数和第三分位数上表现出了显著的影响。这里，短期债务给出的最低的LGD影响，其他贷款具有最高的LGD影响。根据0.75分位数，债务类型会导致8个百分点的波动。AAA级贷款在很大程度上决定了中位数。A、AA级的贷款可能会创造出61个百分点，与同等级别的其他债务相比，它是在中位数情形中的更高的损失。在第三个四分位点，相比同等级别的其他债务，AAA级贷款会降低损失18.6个百分点。

关于信用质量因素，这里可以看到QR的优势：OLS提供了24.5个百分点的变动，它没有区分分位数的高级别。相反，QR所表现出的变动范围是56.5个百分点，事实上，在第50个分位数上，有7.5 (AAA级)+49.0(A,AA级)=56.5。

另外，我们证实了抵押是影响可违约贷款的回收的重要的因素。房产抵押会降低LGD高达51.7个百分点。其他的抵押类型会降低26.8个百分点。OLS会有超过50个百分点的低估影响，为13.5和23个百分点。

本文观测到了主要在第三个四分位数处的行业的影响。不同的行业之间的影响程度的差距最高可达40.8的百分点，其中煤炭矿产行业具有最低的LGD影响系数为-0.1902，批发零售和服务行业具有最高的LGD影响系数为0.2177。相反，OLS会得到错误的结论，因为煤炭矿产行业的行为没有被识别为统计学显著的不同于金融保险行业。

对于宏观经济变量，在中位数情形有一个GDP增长率的降低，系数为-0.0818，即表明经济增长的较差的发展，损失显著的上升。对于第三个四分位数，只有期限价差影响是显著的系数为0.0724，更高的期限价差也生成了较高的损失。再一次，OLS低估了宏观金融协变量的影响，系数分别为-0.0463和0.0131。而对于极端的分位数，模型没有识别任何宏观经济的影响。

总之，QR的参数估计会因分位数的不同而不同，并且估计结果与OLS十分的不同。显然，从更为综合的视角来看，分位数回归QR拓展了标准的回归的结果。协变量的影响会在分位数之间显著的变化，这是对控制变量经济学影响的新启示。

2.模型结果检验

为了检验分位数回归在估计LGD方面的优势，本文在对分位数回归模型进行检验的同时，也将在同样的检验测度指标下，对比分位数回归模型与其他四个模型的绩效，即标准的OLS模型、Beta回归模型(BRM)、分数响应模型(FRM)和有限混合模型(FMM)。

由于Beta回归模型(BR)和分数响应模型(FRM)都有一个潜在的假设：依赖变量是一个比率，即位于0和1之间。而对于实际的LGD，由于存在管理费用，法律成本和清偿费用或者财务费用(费用和佣金)以及较高的抵押回收，因此实际LGD通常要超出0和1范围。为了在对比中运用模型BRM和FRM，我们将实际的LGD变换到了0和1区间中，具体的变换公式为如下

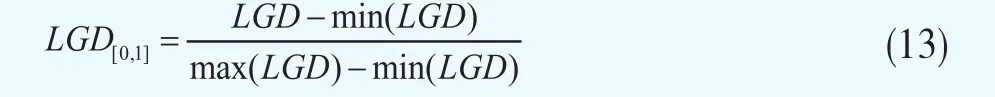
实际的LGD经过转换之后，LGD[0,1]近似服从正态分布。实际上这种转换类似Perraudinand Hu(2006)[9]所采用的逆正态回归转换，其中利用正态分布的逆累积密度函数对LGD进行了转换。

利用模型BRM和FRM基于LGD[0,1]实施估计之后，我们将会对被预测的估计值重新进行再变换，使之回到实际LGD的刻度上来。

对于标准的OLS模型和有限混合模型(FMM)来说，我们没有对实际的LGD进行转换，而是使用了原始的数据来实施估计和对比。事实上，这两类模型没有依赖变量属于[0, 1]的假设，它们可以直接模型化取值确切为0或者1的数据，此时数据变换反而会降低模型的拟合优度。

下面在拟合优度R2、HMI、HWMI和KS这四个测度指标下，从样本内和样本外两个角度，对比QR与其他的4个模型。我们没有仅仅局限于分析均值，而是分析了整个分布的拟合状况。

(1)样本内对比检验

首先，我们检验了全样本的拟合优度。基于整个时期的全样本数据，我们估计了所有模型的样本内取值。表4给出了所有模型的样本内拟合度的四个测度指标值。此外，表4也报告了所有模型的p-值，如果p-值较低，则表明对分布充分拟合的原假设的拒绝。

从表4可知，所有的模型的R2取值都较低，介于0.077和0.101之间，这是由于LGD的双峰特征所决定的。

在所有的模型中，只有QR给出的HMI和HWMI的取值最低，其中HMI=0.0030，而HWMI=0，两个指标都低于0.001的显著性水平，而其他的模型的两个指标的取值分别为0.0480～0.1644和0.0020～0.0179都超过了0.001。

根据KS检验，在0.05显著性水平下，除了QR之外，基于全样本计算的KS检验拒绝了其他的四个模型的原假设，这表明分位数回归QR的拟合效果最好。

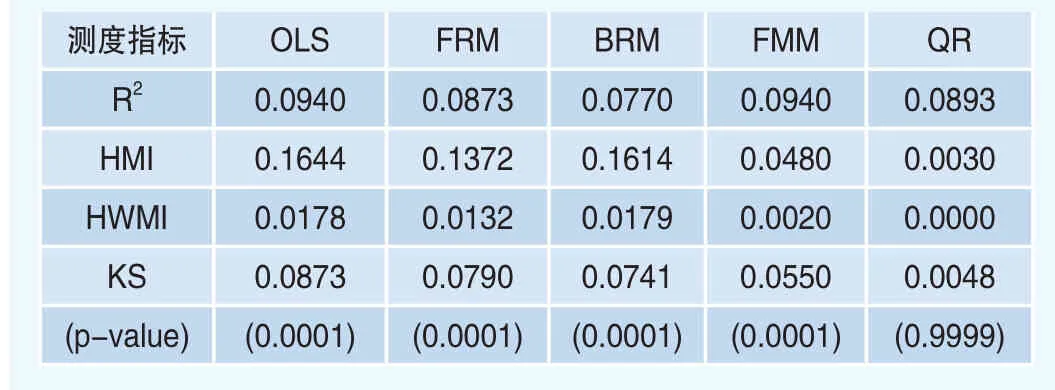
表4 模型样本内检验的结果

另外，也可以利用Michael(1983)[8]提出的P-P图直观的展示分布拟合的精确水平，它可以对比理论分位数和经验分位数，PP曲线越靠近对角线表明理论分位数同经验分位数相匹配程度越高。图5给出了五个模型的P-P图。

从图5的各个模型的PP曲线与对角线的靠近程度可以看出，分位数回归QR估计的LGD的理论分位数和实际LGD的经验分位数几乎是完全拟合的，而其他的四个模型的PP曲线，都表现出了在尾部或中部的系统性的偏倚。显然，根据PP图给出的信息，模型几乎拟合了每一个分位数的样本内的数据，所以说分位数回归QR的样本内拟合几乎是完美的，这正是分位数回归模型相比其他的均值回归模型的优势所在。

综上所述，从对LGD的均值拟合来说，分位数回归QR会导致一个相对适中的样本内拟合。然而，如果考虑到LGD所服从的整个分布，分位数回归QR则表现出了显著的优势，因为样本内拟合优度表明，每一个分位数都几乎被确切的拟合了。

(2)样本外对比检验

为了实施样本外检验，我们把所有的数据划分成用于估计的训练样本和用于预测的检验样本。训练样本包括2000～2009年的子样本数据，该子样本大约是全部数据的60%。检验样本是从剩余的2010～2013年的数据中随机抽取了10000次，所构成的子样本组合，其中每一步中都包含300个可违约贷款，它在我们的数据集合中近似为每年违约的平均次数。

首先基于训练样本我们估计了所有的模型，然后基于检验样本计算了每个子组合的拟合优度，并且汇报了所有10000次步骤的数据的均值，见表5。

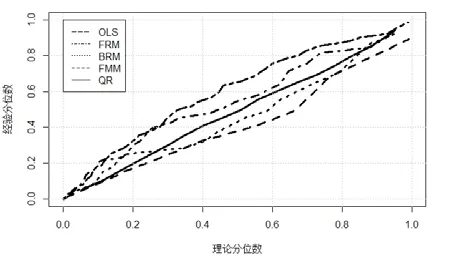
图5 样本内拟合的P-P

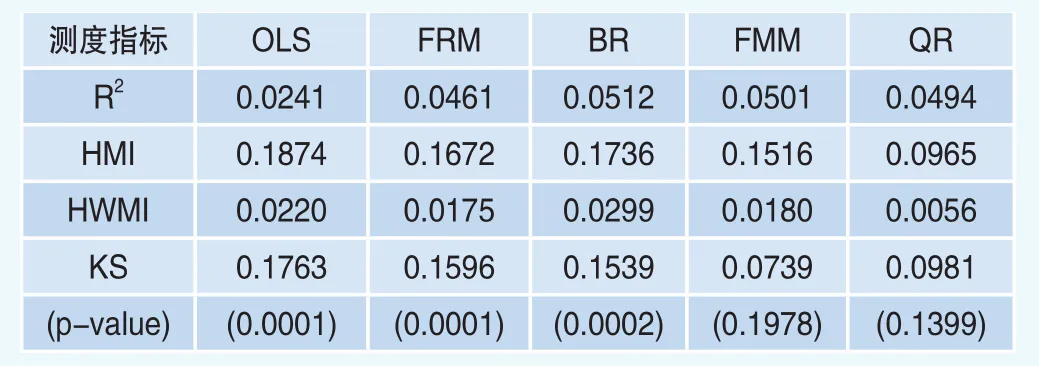
表5 模型样本外检验的结果

表5所示，QR给出了均值的较为适中的拟合，其可决系数R2为0.0344，而基于其他四个模型计算得到的R2取值介于0.0241和0.0512之间。对于测度指标HMI和HWMI来说，QR的取值是分别为0.0965和0.0056，而对于其他的方法来说，取值位于0.1516～0.18748和0.0175～0.0220。显然，分位数回归QR的取值是最佳的。对于KS检验来说，除了FMM和QR大于5%之外，其他的三个方法的平均p值都要低于1%。事实上，在KS检验中，基于三种显著性水平10%，5%和1%，对于FMM的拒绝率为55.7%，41.4%和18.8%，对于QR的拒绝率为89.0%，81.6%和57.3%。

3.违约损失率分布预测

在理论上，应估计每一笔贷款的模型并进行预测，但因为协变量的特定选择会影响到贷款LGD的分布，所以本文仅选择其中某个行业的典型的短期贷款，债务人全部来自煤炭行业。宏观经济和金融状况被选为中间性的场景，即GDP增长率假设为6%，期限价差为2.63个百分点。其他的协变量是从煤炭行业的典型情形中选择的。

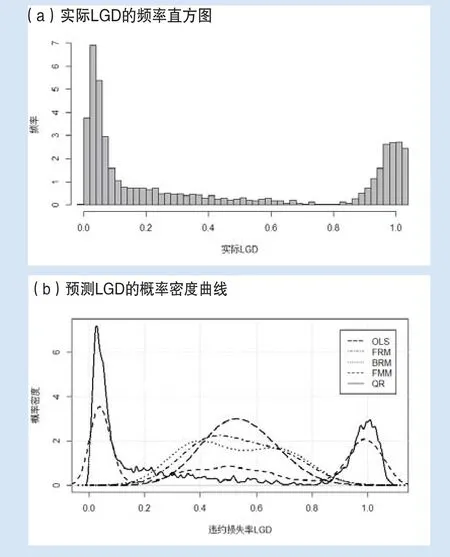
图6 实际LGD与预测LGD的分布

首先利用全样本数据进行了模型的参数估计，然后针对该典型贷款的相应的协变量，对LGD进行了预测。图6(a)给出了该典型贷款的实际LGD的频率直方图，图6(b)给出了该典型贷款的LGD的概率分布密度曲线的预测。

从图6可以看出，标准的OLS模型和分数响应模型FRM都不能捕获LGD的非正态性。虽然这两个方法预测到了分布的中部和尾部的较多的概率，但是对于总的损失来说过小。贝塔回归模型BRM虽然捕获了非正态性，但是也不能捕获已实现的极端的双峰形状。

有限混合模型FMM给出了较为灵活的密度形状。它捕获了双峰特征，并且预测到了在零和1附近的极端值的情形。不过，对于较为稀少的中间部分却给予了太多的概率。

分位数回归QR看起来给出了最佳的预测。较好的拟合了左右两个尾部和中间部分的形状。最小值和最大值意味着较为准确的分布密度的估计。0和1附近的尾部拟合的较好，非常极端的值较少，相比尾部，中间部分的预测也是较为充分的。

结论和进一步研究的方向

已有的各种损失模型主要关注均值预测。然而贷款损失数据表明违约损失率LGD具有强烈的变异特征，而且损失分布具有极端的偏斜和双峰特征。但是，大多数现存的模型和均值预测的校验都没有解释这种行为。为此，本文提出了基于分位数回归的LGD建模方法。它考虑了协变量对LGD的影响随着LGD的整个分布的不同范围而变化，并且反映了损失的较强的不确定性。我们的结论表明，较低的LGD对具有信用级别、保证和抵押个具有较高的敏感性。在中位数情形下，LGD会额外的受到抵押类型，财务类型，还有行业和宏观经济环境的影响。而较高的LGD则没有受到任何协变量的影响。这表明总损失的剩余的尾部风险不能被银行实践或者监管者所控制。此外，我们也使用了校验模型预测绩效测度的新的测度指标。样本内和样本外的分析表明，同大多数现有的模型方法相比，QR优于其他信用风险模型。另外，研究发现宏观经济和金融状况的影响会随着LGD分位数的不同而变化。

基于本文提出的量化LGD的分位数回归模型，可以构建一套完整的贷款违约损失率估计和违约风险预测体系，为商业银行进行贷款风险调整定价、经济资本计算和资产支持证券或者信用衍生品的定价提供重要的借鉴。从而提高我国商业银行在贷款的违约损失率的计量科学性，有助于防范和处置不良贷款问题。另外，本文的模型也有助于金融监管部门在制定信用风险加权资产等规则方面提供新的方法启示。

本文的不足之处在于，限于数据可得性，只是使用了某家城市商业银行的部分数据，而没有对更大范围的数据验证本文模型的有效性，从而无法校验“区域性特征”对LGD的影响程度，而“区域性特征”可能是中国银行业在贷款发放时经常考虑的一个重要因素。因此下一步研究思路就是利用更大范围的数据样本检验模型的适用性。

注释