机械臂神经网络控制优化与仿真

许洋洋,王 莹,薛东彬

(1.郑州工业应用技术学院 机电工程学院,郑州 451150; 2.河南工业大学 机电工程学院,郑州 450007)

机械臂涉及机械、电子、控制、传感器及计算机等多学科发展方向,是衡量一个国家智能化发展的重要依据[1-2].企业采用机械臂进行自动化生产,具有以下优点:① 提高生产率;② 降低生产成本;③ 提高产品质量.机械臂广泛应用于医疗、海洋、航空等领域.由于传统机械臂大多执行简单重复劳动,对运动轨迹控制要求不高,致使机械臂在运动过程中,其轨迹运动的稳定性得不到保证.一旦遇到紧急情况或执行特殊任务,机械臂运动轨迹就会产生较大的偏差,特别是在高速、高负载运动时,运动轨迹产生误差更大,甚至出现严重的抖动现象.因此,研究机械臂高精度、高稳定性控制方法,对于促进整个社会的发展具有重要意义.

随着机械臂应用领域的拓展,机械臂控制要求也在逐步提高,对机械臂控制方法的研究也在不断改进.文献[3-5]研究了柔性机械臂滑模控制方法,创建柔性关节机械臂模型,设计了干扰观测器,引用了滑模控制器,通过仿真验证机械臂输出误差和系统输出的稳定性,从而提高机械臂运动轨迹的反应速度和跟踪精度.文献[6-8]研究了机械臂径向基函数(Radial Basis Function，RBF)神经网络控制方法,建立机械臂柔性模型,给出系统的动力学方程式,设计了机械臂末端RBF神经网络控制器,解决机械臂控制输出的强耦合问题,通过仿真验证机械臂RBF神经网络控制器输出精度,从而提高了柔性机械臂关节运动的稳定性.但是,机械臂末端连杆在复杂环境条件下工作时,其输出轨迹不能按照理想要求进行跟踪.对此,本研究创建了机械臂三连杆运动简图模型,根据拉格朗日方法给出了机械臂动力学方程式,引用了RBF神经网络控制方法,采用混合算法优化RBF神经网络控制器,将改进的RBF神经网络控制器用于机械臂末端连杆运动轨迹跟踪控制.通过Matlab软件对机械臂末端连杆运动轨迹跟踪效果和输入转矩控制进行仿真实验,并与RBF神经网络控制器控制效果进行对比分析,为提高机械臂末端连杆运动精度研究提供了参考价值.

1 多连杆机械臂模型

本文采用多连杆中的三连杆机械臂为研究对象,三连杆简图模型如图1所示.

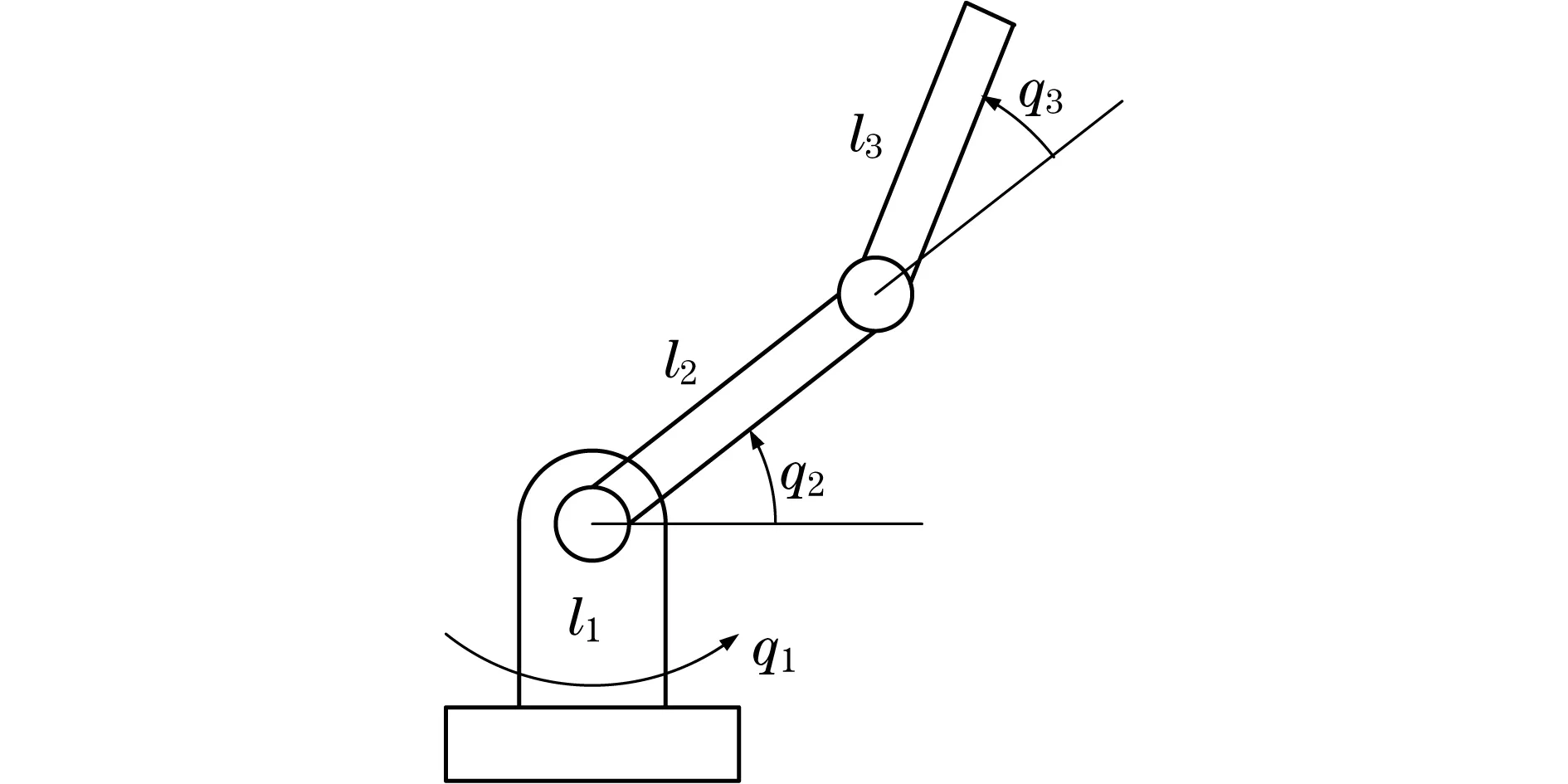
图1 三连杆机械臂平面简图Fig.1 Planar diagram of three link manipulator

在图1中:q1,q2,q3分别为连杆1、连杆2、连杆3的角位移;m1,m2,m3分别为连杆1、连杆2、连杆3的质量;l1,l2,l3分别为连杆1、连杆2、连杆3的长度;g为重力加速度.

根据拉格朗日定律,可以推导出三连杆机械臂动力学方程式[9]如下:

(1)

式中:H(q)为机械臂的惯性矩阵;C(q,q′)为机械臂的离心力和哥氏力组成的矩阵;F(q′)为摩擦力组成矩阵;G(q)为重力组成矩阵;τ为控制力矩组成矩阵;τd为环境干扰矩阵.

2 RBF神经网络控制器

2.1 RBF神经网络结构

RBF神经网络结构如图2所示,主要由3层网络结构组成,输入、输出层之间的映射通过非线性连接,而中间、输出层之间的映射是线性的.RBF网络中的函数采用的是高斯基函数,可加快学习速度,避免出现局部极小值问题,同时，能够提高设备控制系统的位置精度.

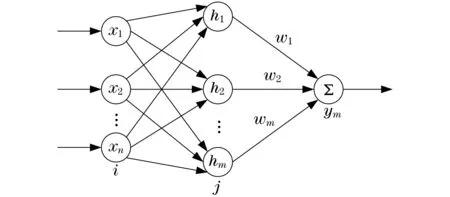
图2 RBF神经网络3层输出结构Fig.2 Three layer output structure of RBF

2.2 RBF算法

在RBF神经网络结构中,高斯基函数[10]为

(2)

式中:X=[x1,x2,…,xn]T为神经网络输入向量;cj=[cj1,cj2,…,cjn]为第j个节点的中心矢量;bj为节点j的基宽度参数.

神经网络的权向量为

(3)

RBF神经网络的输出方程式[10]为

(4)

RBF神经网络的控制目标函数为

(5)

采用梯度下降法,可以得到RBF神经网络控制参数的迭代算法[10]为

式中:η为学习速率;α为动量因子.

根据式(2)可知,高斯函数的性能与参数bj,cj的取值有关.bj影响高斯函数的宽度,bj越小,高斯函数越窄,网络输入覆盖范围越小,敏感性越强,反之敏感性就越差.cj影响高斯函数中心点的坐标,cj与网络输入值相差越小,网络输入敏感性就越好,反之就越差.

因此,采用RBF神经网络对设备输出进行控制和辨识时,中心位置cj和基宽参数bj的选取对神经网络输出控制性能影响较大,如果参数值选取不当,导致高斯基函数无法得到有效映射,从而造成RBF神经网络无效.

3 改进RBF神经网络控制

3.1 约束主导原理

在约束的目标函数中,为了区别可行解和不可行解,定义一个约束主导原理.在满足一定条件情况下,解xi可以主导另外解xj,有3种情形:①xi为可行解,xj为不可行解;②xi,xj都为不可行解,但是,xi总体约束超出值小于xj;③xi,xj都为可行解,且xi适应值大约xj.

为了求解每个解的不可行程度,定义一个数学模型[11]:

(11)

式中:gj(xi)为不等式约束,gj(xi)<0;hk(xi)为等式约束;J为不等式约束个数;n为等式约束个数;xi为获得的解.

为了缩小搜索可行解范围,在进化中选择模拟退火的概率突跳机制,比较个体的不可行度和阀值,决定是否采用.不可行度阀值[11]为

(12)

式中:tm为模拟退火温度;m为循环次数,Npop为种群个数.

3.2 混合粒子群算法

粒子群优化算法采用一群粒子通过一定速度在D维搜索空间中飞行,每个粒子的飞行速度、位置通过比较个体和群体进行更新,其速度和位置更新方程式[12]为

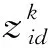
标准粒子群算法在搜索过程中,容易陷入局部最优解,搜索全局最优解相对困难.因此,在粒子群算法中引入交叉算子、变异算子和模拟退火机制.模拟退火具有概率突变的能力,可以避免搜索过程中产生局部最优解.利用遗传算法的交叉和变异保持种群的多样性.

3.3 改进RBF神经网络控制

(1) 对模拟退火温度[11]进行初始化

(15)

式中:pworst,pg分别为种群最差和最优个体;pa为可接受概率.

(2) 交叉生成新的个体

(16)

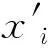
(4) 如果用子粒子替换母粒子,则子粒子飞行速度[11]为

(17)

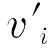
(5) 变异生成新的粒子群

(18)

式中:G(u,σ)为高斯随机分布;u为期望;σ为标准差.

(6) 通过指数降温方法,设置模拟退火衰减控制参数λ,使温度变化为tm+1=λtm;转到步骤(2),如果进化迭代次数达到最大或满足结果要求,则停止运算.

步骤(2)采用交叉概率pc,可以维持种群个体的多样性.步骤(3)根据约束可行性判别方法,采用模拟退火算法进行个体突跳选择,避免粒子群算法出现局部最优解,从而搜索到全局最优解.对于机械臂末端控制一般采用两个神经网络,其中一个为在线辨识,而另一个作为控制器,机械臂运动轨迹输出误差作为神经网络控制输出,混合算法优化RBF神经网络控制结构如图3所示.

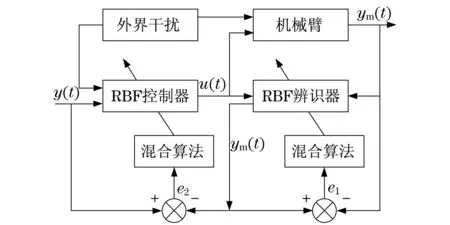
图3 机械臂改进RBF神经网络控制器结构Fig.3 Improved RBF neural network controller

4 仿真效果分析

三连杆机械臂末端连杆运动时,连杆1运动驱动连杆2带动连杆3.因此,连杆3执行任务时,会产生一定的误差.本文采用软件Matlab对机械臂连杆3运动效果进行仿真,运动参数设置为:机械臂连杆3假设角位移曲线为方波,初始角位移为q(0)=[0 0 0]T,外界干扰为τd=10sin(2πt),机械臂连杆长度为l1=l2=l3=1.0 m,机械臂连杆质量为m1=m2=m3=1.0 kg,重力加速度为g=10 m/s2,网络学习参数α=0.05,η=0.35,仿真时间为t=4 s.假设在无干扰情况下,采用RBF神经网络控制器和改进RBF神经网络控制器跟踪效果如图4所示,采用RBF神经网络控制器和改进RBF神经网络控制器输入转矩如图5所示.假设在有干扰情况下,采用RBF神经网络控制器和改进RBF神经网络控制器跟踪效果如图6所示,采用RBF神经网络控制器和改进RBF神经网络控制器输入转矩如图7所示.

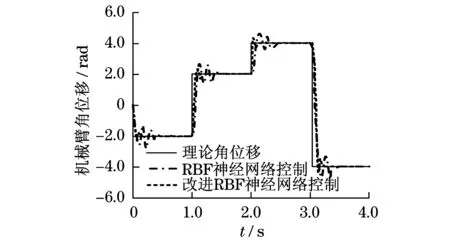
图4 连杆3角位移(无干扰)Fig.4 Third link angular displacement (no interference)

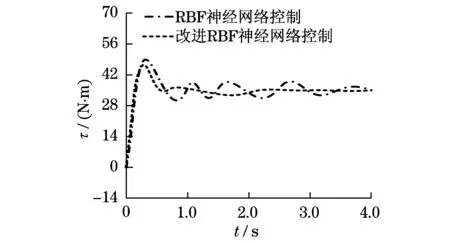
图5 连杆3转矩(无干扰)Fig.5 Third link torque (no interference)

在无干扰情况下,根据图4和图5可知:机械臂连杆3采用RBF神经网络控制器和改进RBF神经网络控制器所产生的跟踪误差相差不大,但RBF神经网络控制器输入转矩较大,跟踪速度较慢,系统存在较大的抖动现象.在有干扰情况下,根据图6和图7可知:机械臂连杆3采用改进RBF神经网络控制器跟踪误差低于RBF神经网络控制器,且改进RBF神经网络控制器输入转矩变化不大,系统运动相对稳定,表现较强的抗干扰性.因此,采用改进RBF神经网络控制器能够提高机械臂运动精度.

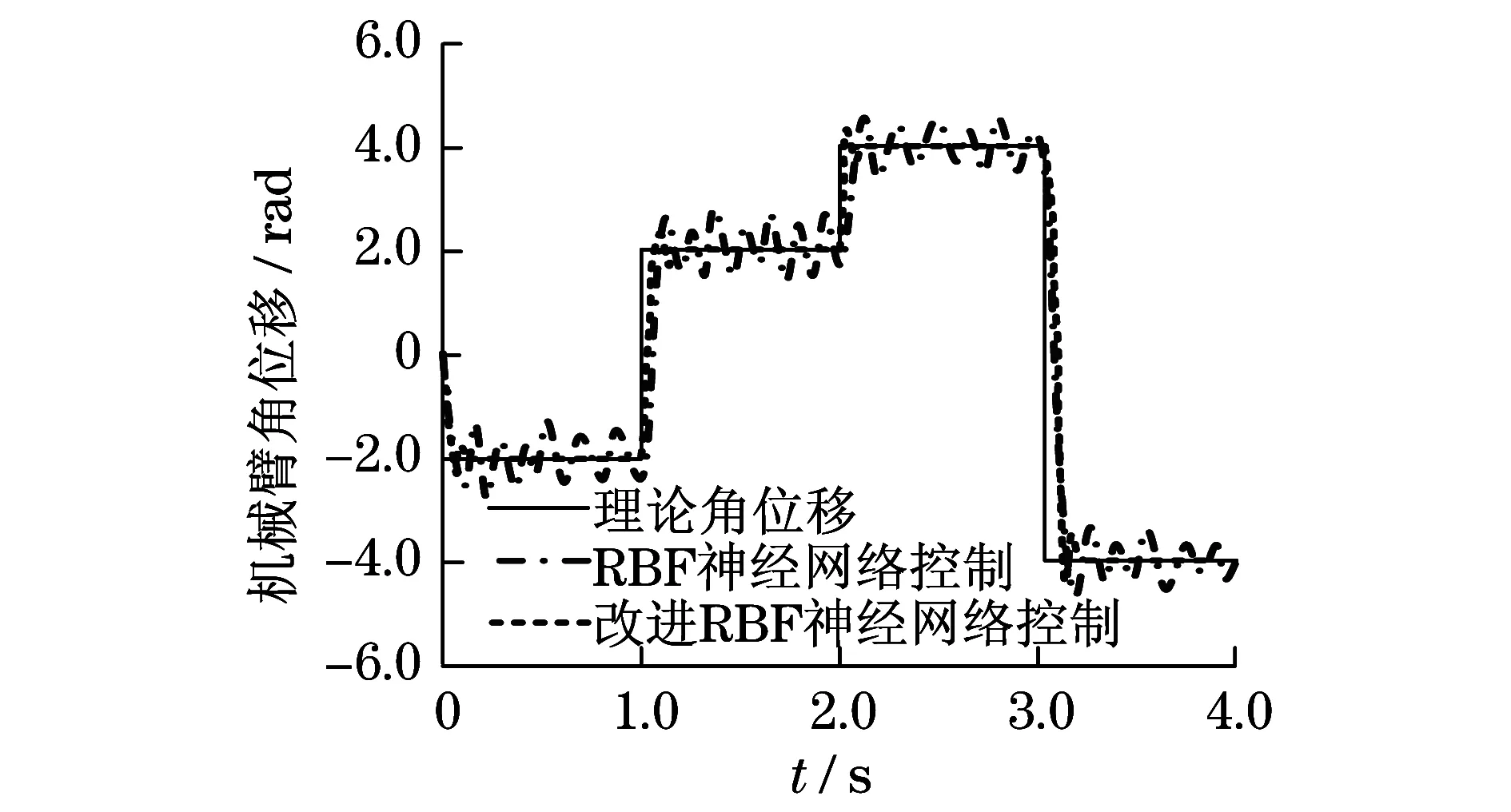
图6 连杆3角位移(有干扰)Fig.6 Third link angular displacement (with interference)

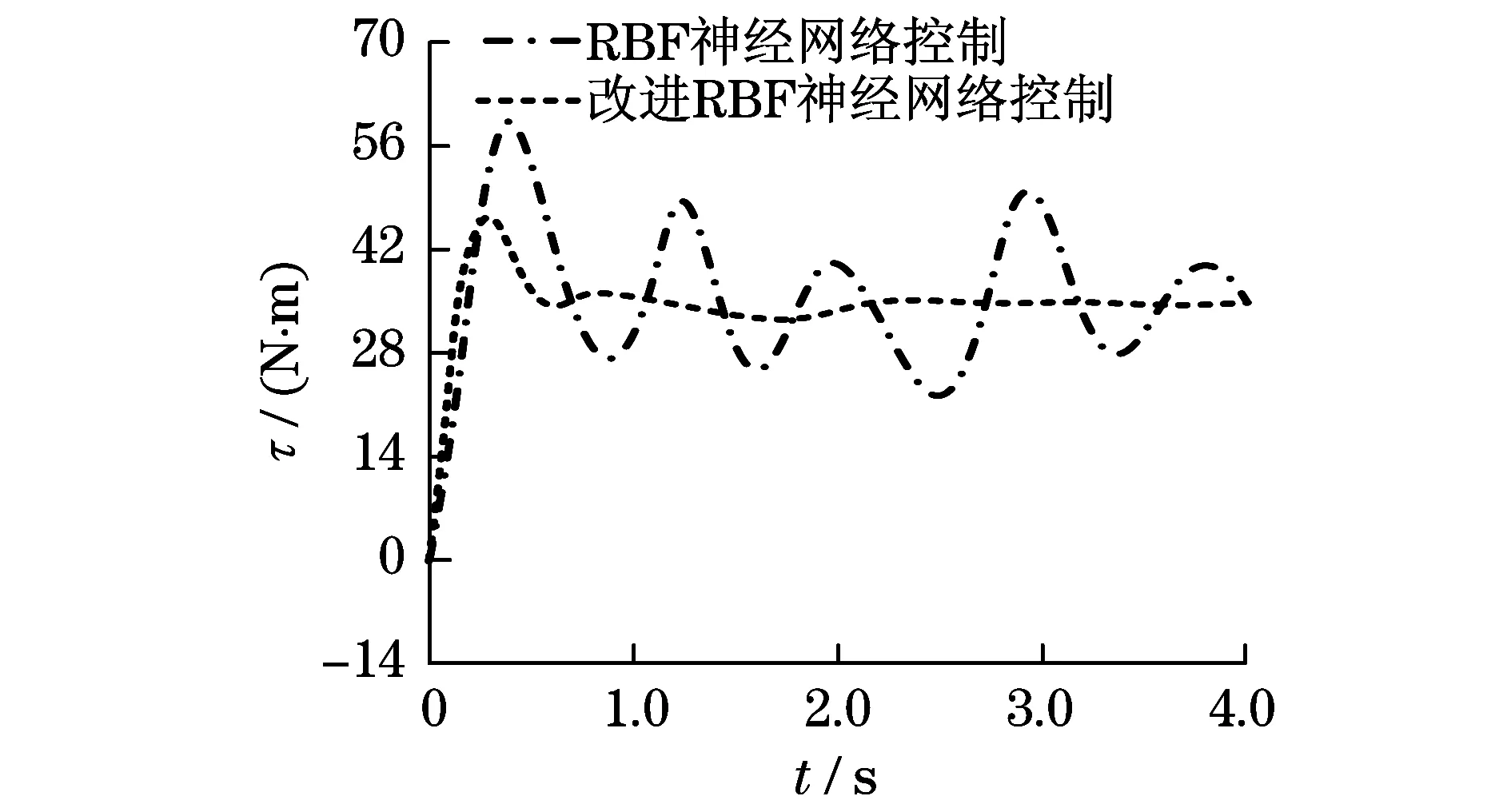
图7 连杆3转矩(有干扰)Fig.7 Third link torque (with interference)

5 结论

针对机械臂末端连杆运动控制问题,采用了改进改进RBF神经网络控制方法,主要结论如下:① 改进RBF神经网络控制器能够抗击外界因素干扰,降低系统输出误差,跟踪速度较快,有效削弱系统振动现象;② 混合粒子群优化算法能够避免局部最优解快速搜索到全局最优解,不仅可以用于机械臂末端连杆RBF神经网络控制器,也可用于机械领域其他目标函数的优化.