叶轮不同叶片对离心泵内流道流场的影响

齐凤莲,刘冠诚,Horia Abaitancei,王永章

(1.沈阳建筑大学 机械工程学院,沈阳 110168; 2.布拉索夫特兰西瓦尼大学 汽车实验室，罗马尼亚 布拉索夫 500001)

离心泵是重要的能量转换和流体传输装置,其工作性能由内部流场内反映出来,被广泛应用于工业、农业以及航天领域.但由于目前国内的离心泵在图纸绘制方式、理论设计方法、性能预测与内部流场分析等方面的研究,远远落后于发达国家，因此,提高离心泵的运行效率,改善离心泵内部流体的稳定性与提高离心泵运行的安全性是各相关领域亟待解决的问题.数值模拟法是优化离心泵的重要手段之一,已有不少学者对其进行了研究[1-4].在国内,大多数采用雷诺时均(Reynolds Averaged Navier Stokes,RANS)法进行数值模拟[5],如有学者[6]利用该方法研究了叶片个数对离心泵的内部流场的影响以及离心泵自身的性能.虽然已经有不少有关离心泵蜗轮盖叶片数对流场影响的数值模拟,但绝大部分停留在RANS法模拟流场的涡型.由于RANS法需要对边界进行网格划分,网格的精细程度影响仿真结果,而且涡型的改变对结果影响很大[7-8].相比于雷诺时均法,大涡模拟(Large Eddy Simulation,LES)由于剔除了小尺度涡旋,虽然其计算结果在空间上的准确度没有直接模拟高,但是它可以获得比RANS模拟更多、更详细的流动信息[9-10].而直接模拟法数据量又非常大,仿真时间长[11]，因此,LES变得越来越有优势,在不久的将来LES将会应用于更多的工程实际[12-13].

本文采用LES的三维数值模拟法对离心泵进行了全流场的模拟,得到了相应的参数化数值,并通过实验对仿真数据进行了合理性的验证.文中展示了离心泵流场的相对速度分布图和静压分布图,分析了蜗轮盖上不同叶片数对离心泵内部流场的分布影响,用进出口压力差计算了不同叶片对扬程高低的影响,通过中心面涡形图分析了流场湍流强度和流场稳定性的关系,同时，探讨了离心泵内失稳较高的区域与解决思路.

1 仿真模型

本文仿真研究以IHF150-125-250为参照对象,以其叶片木模图和轴面投影图为建模参考量,采用CATIA建模软件对泵叶片进行曲面造型(该叶片为扭曲型叶片),并进行阵列得到需要的均布叶片个数.本次数值分析叶轮个数从3至7.图1和图2分别为单个叶片的叶片木模图和扭曲型叶片轴面投影图,图3为扭曲六叶片蜗轮盖的三维模型.

图1 叶片木模图Fig.1 The wood model diagram of blade

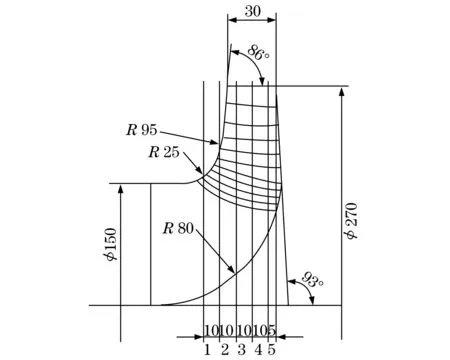
图2 扭曲型叶片轴面投影图Fig.2 The axial projection diagram of twisted blade

图3 扭曲六叶片蜗轮盖三维模型Fig.3 Three-dimensional model diagram of twisted

图4和图5分别为蜗壳的水力模型图、蜗壳断面图，其中T为蜗壳二维截面直线的相切点，H为截面直线的长度.图6为蜗壳水体的三维模型.

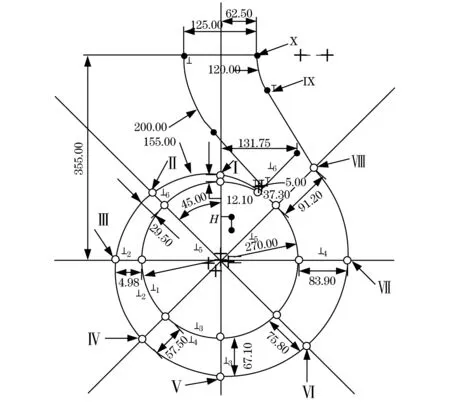
图4 蜗壳水力模型图Fig.4 The hydraulic model diagram of volute

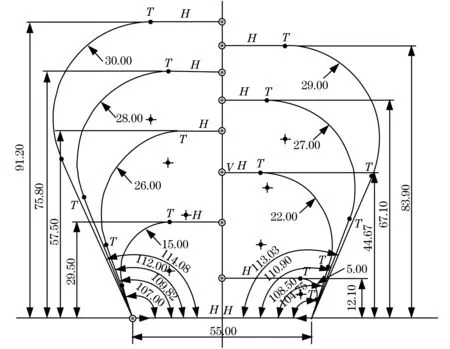
图5 蜗壳断面图Fig.5 Volute cross-section diagram

图6 蜗壳水体三维模型Fig.6 Three-dimensional model diagram of

2 模拟方法

本文模拟方式采用大涡模拟LES，其模拟思路为直接数值模拟大尺度紊流运动，利用次网格尺度模型模拟小尺度紊流运动对大尺度紊流运动的影响.LES控制方程组在RANS方程组的基础上进行无量纲化和滤波，进而得到LES的优化方程组.在复杂流动的模拟仿真中，基于离散相模型的LES可以得到很多基于多流体模型的RANS方法无法获得的流场细微结构和流动图像.

2.1 条件设置

对小流量、设计流量、大流量等不同流量进行模拟,蜗轮转速为1 450 r/min.LES不需要手动进行网格的划分,更接近于直接数值模拟.入口边界采用速度流入,出口边界采用自由流动.

2.2 控制方程

常见的三维可压流的RANS方程组包含3组方程：3个分速度的动量方程、质量方程和能量方程.本文在RANS方程组的基础上进行量纲化，再对其量纲化方程组进行滤波，得到了LES的控制方程组：连续方程、动量方程和能量方程.

连续方程

(1)

且有

(2)

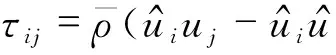
动量方程

(3)

能量方程

(4)

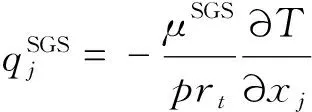
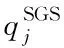
3 仿真模拟合理性验证

在详细仿真之前需要验证仿真的准确性.由于设备的限制,通过“仿真-实验”法仅对六叶片蜗轮的离心泵进行仿真的准确性验证.对比相同工况下的实验数据,当仿真数据在误差允许的范围内,则证明仿真数据合理准确.

图7为清水介质的额定流量工况下，离心泵整机流道内流场的速度矢量图和静压图.从图7(a)的速度矢量图可以看出：在整机流道范围内，叶轮进口处相较流道其他区域流体流速最低，但流动较为均匀，各方向速度梯度均比较小，此处发生水力损失也较小；待流体进入叶轮通道后，其速度在不断增加，特别是沿着叶轮直径的方向，速度值增加明显，直到流体从叶轮出口处流入蜗壳流道内；流体进入蜗壳后，顺着叶轮旋转方向流向蜗壳出口，在此过程中流体的速度在不断减小；虽然叶轮截面关于旋转轴中心对称，但是其内部流场却存在非轴对称性，此时泵的水力损失增加；蜗壳内流体基本上是沿着叶轮的旋转方向在流动，速度逐渐地减小，除在隔舌附近位置之外蜗壳内速度分布比较均匀，沿着叶轮径向的方向，速度均匀性越强；流体到达蜗壳出口位置时，速度分布更为均匀且大小与进口速度大致相等.从图7(b)的静压图可以看出：流体在进入叶轮之后，静压值在不断的增加，从叶轮流道进入蜗壳后，静压值依旧在增加，但是增加幅度较小，原因是叶轮内静压迅速增加是由于叶轮对流体的做功作用，而蜗壳内静压的增加主要是动能向静压能的转化，并在出口截面完成能量的转化使静压最大.从对离心泵整机流道内速度矢量场、压力场的联合分析可以看出，数值模拟结果基本上符合离心泵内流体的真实流动[14-16].

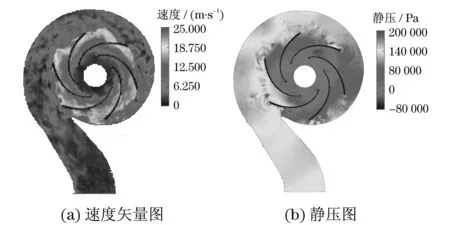
图7 整机流道内的绝对速度矢量图和静压云图Fig.7 Absolute speed vector diagram and static pressure

通过仿真与实验的对比来验证仿真的合理性.图8为仿真与实验条件下的扬程-流量(H-Q)对比图.从图8中可以看出：大于400 m3·h-1流量下扬程偏差低于3%，在所有流量条件下扬程偏差不大于5%，均在误差允许范围内.

图9为仿真与实验条件下效率-流量(η-Q)对比图.从图9中可以看出：仿真条件下与实验条件下效率在不同的流量下数值接近，且仿真数值略高于实验数据，符合实际情况，并且两条曲线走势相同.

因此，本次仿真数据有效可靠,可进行详细的数据处理和分析.

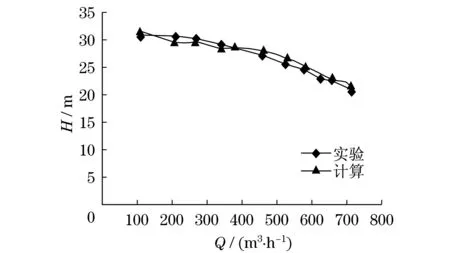
图8 H-Q对比图(n=1 450 r·min-1)Fig.8 H-Q comparison curves(n=1 450 r·min-1)

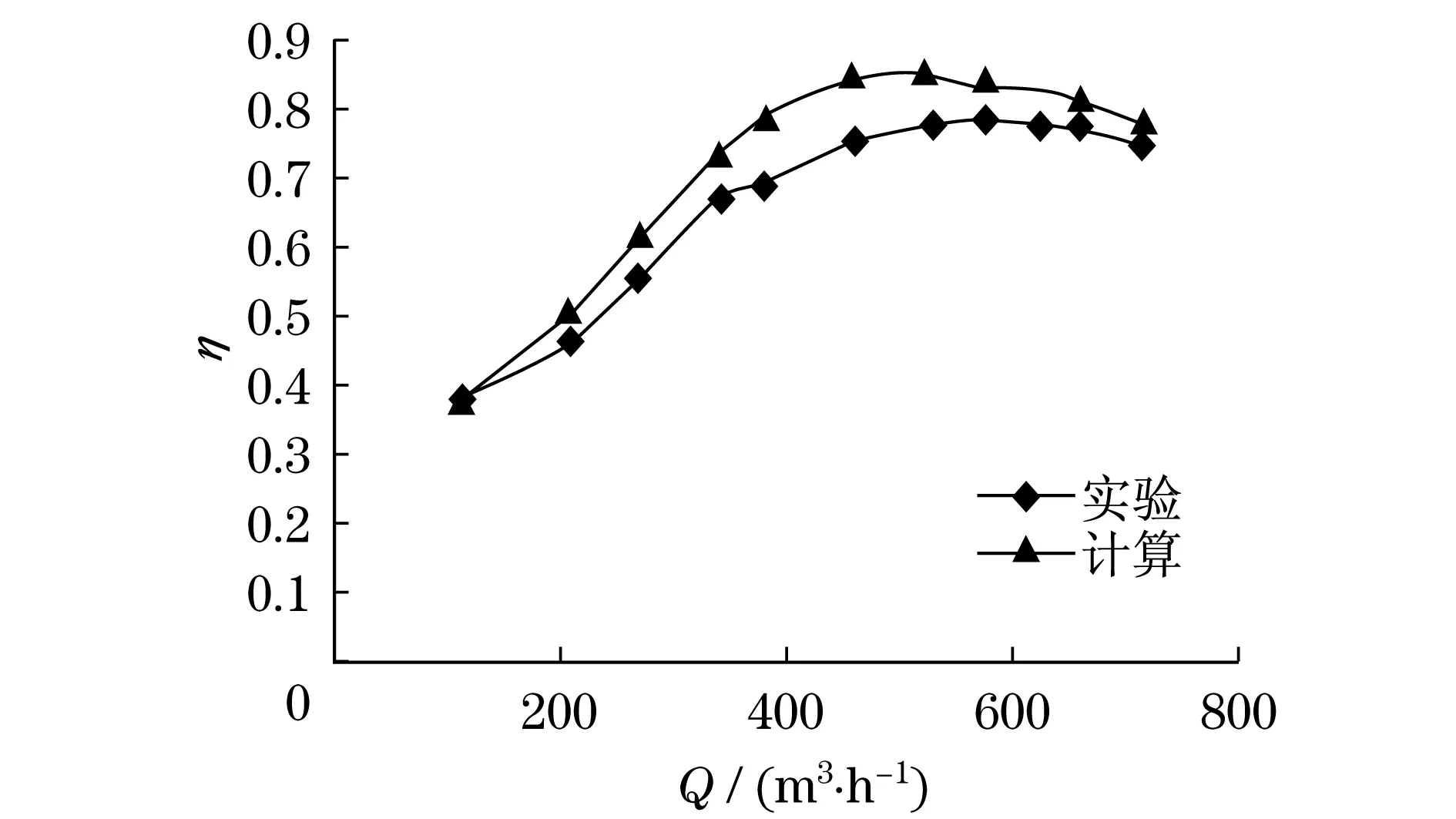
图9 η-Q对比图(n=1 450 r·min-1)Fig.9 η-Q comparison curves(n=1 450 r·min-1)

4 仿真结果分析

从计算域组成的角度来看，离心泵内流场的流动情况主要由蜗壳、叶轮等过流部件的几何形状及结构尺寸所决定.叶轮是离心泵的核心部件，离心泵整机流道内的流体运动形式、流场状态受叶轮形状和运动形式影响最大，并且叶轮中的流体运动形式为复杂的复合运动.因此，结合速度场、静压场来分析泵内流体的流动情况对泵的优化设计及高效运行都具有重要的意义.以下将结合数值模拟的结果重点对扭曲叶片叶轮内流场的速度和压力进行分析.

4.1 离心泵H-Q特性分析

图10为叶片数3,4,5,6,7,8下离心泵的H-Q对比曲线.从整体来看，不同叶片下扬程曲线走势相近.但在不同叶片下，扬程的数值有较大不同.在小流量下，流量对扬程影响较小，曲线的斜率较为平缓.在设计流量下，5，6，7，8叶片下的扬程反而出现了正向斜率.在大流量情况下，斜率变化较快，但扬程不是随着叶片数的增加而增高，叶片数为7的扬程值反而低于叶片数为5和6的扬程值.究其原因，流体在叶片3到5离心泵中做的功大于叶片表面和泵壳摩擦力损失的能量，叶片在3到5的区间内总能量随叶片增加而增加，扬程随之增加.叶片在5和6区间内，液体做的正功和摩擦力损失的负功基本一致，在此区间内总功基本不变，扬程也基本不变.在6到8叶片区间内，由于叶轮的叶片数量增加，叶片的表面积总和增大，受叶片表面粗糙度所做的负功大于液体所做的正功.在此区间内总功随叶片数增加而减小，导致扬程降低.

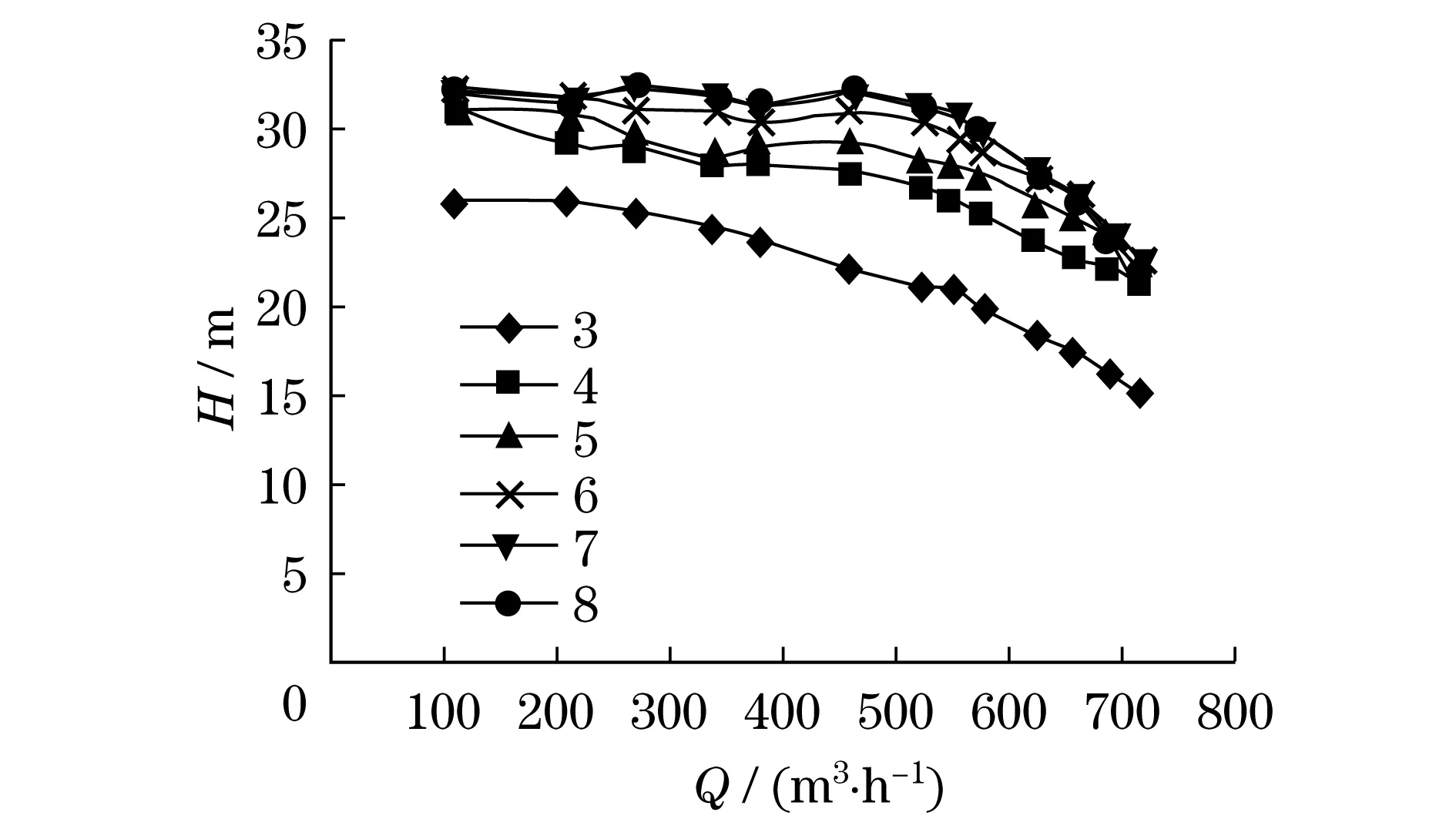
图10 不同叶片数离心泵H-Q对比图

图11为叶片数3,4,5,6,7,8下离心泵的η-Q对比曲线.从整体来看,不同叶片下效率曲线走势相近,尤其是在小流量情况下,不同叶片的效率值几乎相同.因此,在小流量条件下,叶片数的不同对运行效率影响不大.随着流量增加,运行效率出现了不同的变化.叶片数为3的运行效率最不稳定,波动幅度较大,曲线曲率变化较大.大流量下,运行效率不是随着叶片数增加而增加,叶片数为5时效率最高,叶片数为4,6,7,8时效率反而降低,且叶片为6,7,8时在效率达到最高点后随流量增加效率降低越来越快.总体来说,不论小流量还是大流量,叶片数为5时效率最好,而且在不同流量时效率变化平稳,没有波动性.由于小流量时不同叶片效率差距很小,过度分析没有太大的意义.本文着重分析大流量下不同叶片对离心泵内流道流场的影响.

4.2 离心泵内流道速度分布分析

图12是不同叶片下离心泵内流道中心平面上的速度分布图.内流道中压力面到吸力面速度变化越平缓，表明流体流动越平稳.从图12中可以看出：叶片数Z=7时，压力面到吸力面速度变化较明显，说明流动相对不平稳；叶片数Z=4，5的流道蜗舌附近可看到明显的射流-尾迹现象，但在叶片数Z=6，7的流道内射流-尾迹现象不明显；叶片数增多，流道内的射流-尾迹现象得到一定的改善；蜗舌与流道的相对位置对射流-尾迹的强弱有一定的影响；叶片数增多，有助于减小离心泵中因射流-尾迹而带来的损失，但当叶片数太多时，相对速度从压力面到吸力面的变化较明显.

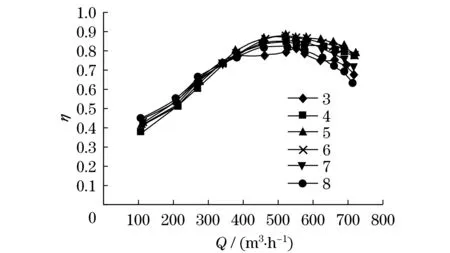
图11 不同叶片数离心泵η-Q对比图(n=1 450 r·min-1)Fig.11 Centrifugal pump η-Q comparison curves of

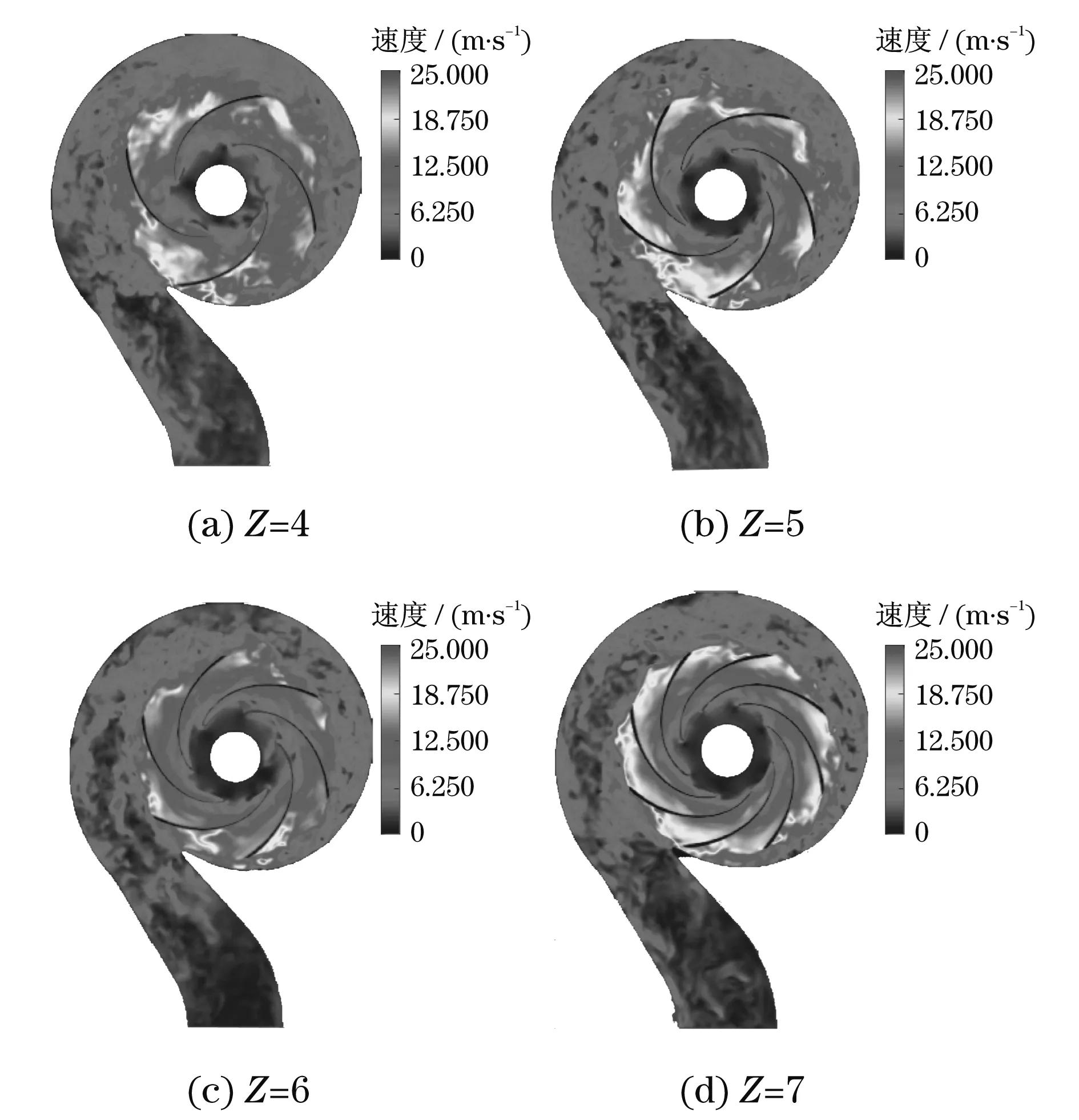
图12 不同叶片中心平面速度流场分布图Fig.12 Center plane velocity flow conditions

4.3 离心泵内流道压力分布分析

图13是不同叶片下离心泵内流道中心平面上的压力分布图.从图13中可以看出：吸力面区域出现了低压区，这是易发生空化的区域；对于不同叶片的离心泵内流场均存在低压区，但相比而言，叶片数Z=5，6的内流场低压区面积相对较小，低压程度较轻；叶片数Z=4的内流场低压程度较重，负压值较大，更易发生空化；叶片数Z=7的内流场低压区面积较大，低压程度相对较重，也更易发生空化.因为叶轮入口处低压区的产生是由于水流流经叶片头部时流体加速转弯，流速加快，导致流体在叶片进口处形成低压区，随后由于叶轮旋转使得叶轮通道内的水流随半径的增大而逐渐增多，压力逐渐增大.同时，随着叶片数的增加，低压区的面积也在增大，故叶片数对离心泵的空化有一定影响.

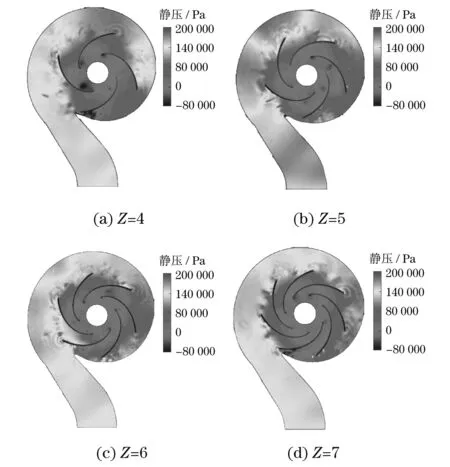
图13 不同叶片中心平面压力流场分布图Fig.13 Center plane pressure flow conditions

流道中压力面和吸力面的压力分布应该分布越均匀越好，且两者之间的压差也是越小越好，如果压力差较大，会使得流体从压力面一侧流向吸力面一侧，会产生回流和漩涡，并造成能量的损失.图13(b)，13(c)，13(d)中叶片数Z=5，6，7的叶轮叶片压力面和吸力面一侧的压差较小，这可能是因为叶片数的增加，使得流道变窄，叶轮内部的流动情况得到了一定改善.随着叶片数的增加，压力面一侧的逆压梯度在不断增大，逆压梯度会导致叶片表面出现逆流，使得流体做负功，降低了离心泵的运行效率.同时受逆流影响，流场漩涡增多，在一定程度上也增大了振动幅度，降低了运行的平稳性，这说明叶片数并不是越多越好.综上，随着叶片数的增加，叶轮部分流道压力分布情况有所改善，但叶片数并不是越多越好.当叶片数Z=5时，流道中压力面和吸力面之间的压差较小，逆压梯度适中，流动性能相对较好.

4.4 离心泵内流道涡形分布

图14是大流量下不同叶片下离心泵内流道中心平面上的涡量流场分布图.图14中浅色区域是流道内涡较大的区域，涡的颜色越浅，则表明湍流强度越大，流体在内流道流动的稳定性越差.从图14中可以看出：不同叶片的离心泵内流场中浅色区域分布规律相似；叶片数Z=4时浅色区域分布较广，颜色深度较为深，流动稳定性一般；叶片数Z=6，7时，浅色区域面积随叶片数逐渐增大，颜色逐渐变浅，说明随叶片数增加湍流强度越来越大，流动稳定性越来越差；流道中不稳定区域主要位于吸力面，这说明在叶轮流道中，流动是最先从流道出口的吸力面开始失稳的，且越靠近蜗舌，流动就越复杂，更容易产生涡；叶片数Z=5时浅色区域较少，颜色深，湍流强度低，流动稳定性好.总之，叶片数Z=5时离心泵湍流强度最小，流场稳定性最好.通过仿真控制涡形的湍流强度，可改进离心泵和叶轮机械的设计.

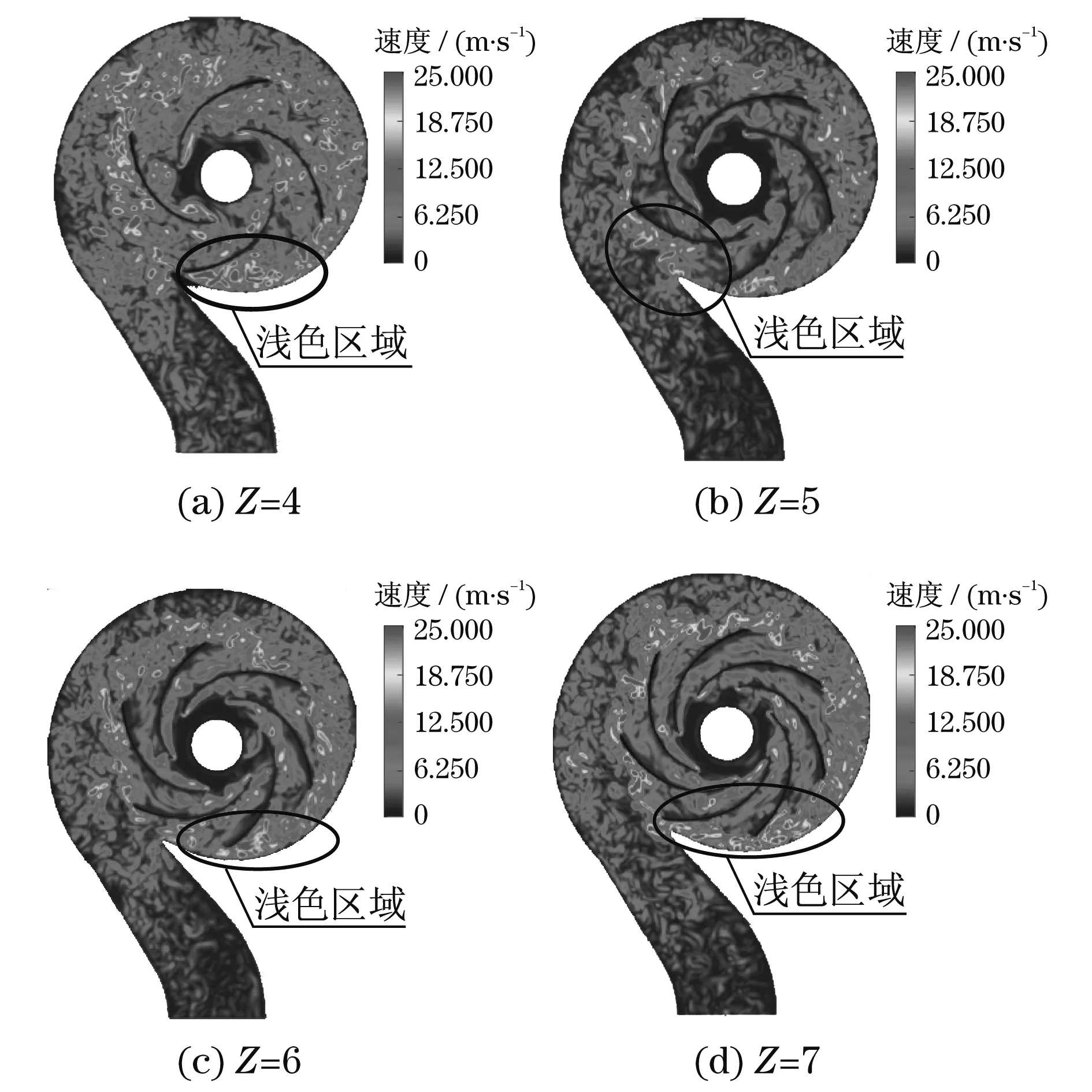
图14 不同叶片中心平面涡形流场分布图Fig.14 Center plane scroll flow conditions

5 结论

本文对离心泵内流体的流动特性进行了三维数值模拟.通过“仿真-实验”法验证了离心泵内流场仿真的准确性，六叶片叶轮离心泵内流场仿真得到的离心泵H-Q特性、η-Q特性与实验结果吻合较好.仿真得到了全流场的参数分布与全流场的涡形分布.主要结论如下：① 随着叶片数增多，压力面和吸力面的压差有所减小，流道内的射流-尾迹现象也有所改善.但当叶片数大于5时，流道增加，流道内部损失也相应增大，流体获得的总功减少，从而引起扬程和效率下降.② 在大流量下，不同叶片数离心泵中心平面上涡量分布规律相似.从涡形分布可知，叶轮部分流道出口部分吸力面附近的湍流强度较大，流动失稳先从叶轮出口部分的吸力面开始.③ 本文所研究的离心泵，在大流量下，当叶片数为5时，效率最高，稳定工作区域大.而在小流量下，叶片数的影响不明显.本文研究结果为揭示离心泵内复杂流动现象的作用机理提供了参考，对离心叶轮机械失速研究、实施流动控制、湍流的理论研究和工程应用都具有重要意义.