小球式旋转直驱压力伺服阀动态特性分析优化
陆亮,夏飞燕,訚耀保,*,原佳阳,方向
1. 同济大学 机械与能源工程学院,上海 200092 2. 南京机电液压工程研究中心 航空机电系统综合航空科技重点实验室,南京 210061
20世纪80年代末期,电机出现了混合励磁同步结构,其输出效率高、力矩大,应用广泛[1-3]。基于高功率密度电机的发展,同期,出现了一批旋转直接驱动伺服阀的专利[4-6],通过运动转换机构将电机的旋转运动转换成阀芯的直线运动,其目的是取消传统两级阀中复杂的前置级。直接驱动电液压力伺服阀拥有结构简单、抗污染能力强等优势,可应用在紧凑型液压系统中替代传统的两级电液伺服阀,其应用优势逐渐体现出来,如在飞机电子防滑刹车系统中取代传统的喷嘴挡板阀作为压力控制元件,避免易发的油液污染颗粒堵塞喷嘴口而使压力控制失效的问题。
近年来,直接驱动的电液压力伺服阀发展迅速。1993年日本学者Urai等[7]提出采用磁致伸缩材料提供阀芯直接驱动的动力,通过通电线圈产生磁场,处于磁场中的磁致伸缩材料发生变形,进而推动阀芯,此种结构的阀结构紧凑,阶跃响应快,但对温度变化敏感。MOOG公司提出以直线力矩马达直接驱动阀芯的直动阀结构,如D633/644系列[8],该系列现已形成产品,其动静态特性良好,但它将直线力矩马达与阀芯同轴布置,结构不够紧凑。2006年以PARK公司为首的音圈驱动[9]单级阀开始发展,将阀芯与通电线圈相连,在外加磁场作用下,线圈带动阀芯移动,同时在线圈上内置位移传感器,用于检测阀芯位置,由于线圈无支承,其惯量小、无摩擦,整阀响应线性度高,但是由于线圈位移有限,其可控的输出流量或压力较小。2016年西安交通大学[10]提出一种转阀结构,在阀芯和阀套上对应开槽,通过阀芯与阀套的相互转动开启或闭合对应的通槽,从而控制输出的流量或压力。这种结构使得污染颗粒难以在阀内堆积,抗污染能力强,且阀芯转动阻尼相对滑动阻尼小,动态特性较优。
伺服阀作为飞机刹车系统中的压力控制元件,其动态特性的好坏,直接影响刹车系统的控制效果[11]。2002年Yuan和Li[12-13]先后提出通过减小滑阀阻尼长度的方法来增加其响应速度,通过在滑阀节流边开槽,将滑阀变为负阻尼可以有效地改善滑阀的动态特性。2009年吴泊宁等[14]根据模态截断的相关理论,推导了闭环系统在不同模态叠加过程中的稳定性变化,得出了伺服阀系统在高频阶段失稳的结论。2014年黄澄等[15]通过时域仿真结合频域分析证明了飞机液压刹车系统管路会影响压力伺服阀的输出特性,两者相耦合会引发伺服阀振荡失稳。2016年逯九利等[16]利用AMESim仿真验证了飞机刹车压力控制系统谐振的原因,并优化选取了管路、系统背压及压力控制阀参数。从系统控制的角度来看,压力伺服阀作为控制系统关键环节,在参数不匹配的情况下,极易形成振荡、失稳问题[17-19]。
针对一款具有开发应用价值的紧凑型旋转直接驱动电液压力伺服阀,在动态特性测试过程中出现的控制压力超调量大、响应调整时间长等现象,建立了闭环系统从输入电信号至输出压力的数学模型,分析传递函数中影响该阀动态特性的重要结构参数和电控方法,优化选取参数及改进电控方法后,通过实验验证整阀的动态响应效果。
1 小球式旋转直驱阀的工作原理及框图
1.1 工作原理
小球式旋转直接驱动电液压力伺服阀(Ball-type Rotary Direct Drive Pressure Servo Valve, BRDDPSV)由有限转角电机、小球-柱形孔运动副、功率滑阀副及反馈传感电子电路组成,如图1所示。
该旋转直驱阀采用有限转角电机驱动,将电机输出轴上偏置的小球插装在阀芯末端等径的柱形孔中,使电机的旋转运动转换成阀芯的水平运动和绕轴线的转动。其中,阀芯的水平运动可控制输出压力,而绕轴线的转动仅为了避免运动干涉。正开口滑阀副为两凸肩、三通的结构形式,滑阀阀芯两端接通回油,阀芯左右两腔压力p1、p2均为0,负载口置于供油口和回油口之间,负载口中的控制压力由阀芯滑动位移来调节:滑阀位移在供油口和回油口间形成联动的节流作用,从而使中间的负载口输出可控的压力[20]。同时,反馈电机转角和控制腔中的压力至输入信号,构成闭环控制。

图1 BRDDPSV结构示意图Fig.1 Structure diagram of BRDDPSV
1.2 数学模型
根据该旋转直驱压力伺服阀工作原理,可建立该阀的数学模型。
经典控制理论为闭环非线性系统提供了线性化处理方法:若系统中的非线性因素较弱,可直接忽略次要的非线性部分;若系统中的变量只是在工作点附近发生了微量偏移,可以应用切线法取其中的线性主要部分,即在工作点线性化。线性化后,以成熟的经典控制线性理论分析问题。
1.2.1 电 机
有限转角电机采用单向绕组,不需要整流电路,转角限制在±30°内。电机转子动力学方程为
(1)
式中:Jr为电机转动惯量;α为电机转角;Tem为电机输出力矩;Br为转动阻尼;TL为负载力矩。
实测电机的输出电磁力矩Tem和转角α的关系曲线为抛物线,采用二阶函数模型对该曲线进行拟合得
Tem=kti0-kmα2
(2)
式中:kt为电流-力矩系数;km为转角-力矩系数;i0为电机输入电流。
在电机转角较小时,输入电流与输出力矩近似呈线性关系
Tem=kti0
(3)
1.2.2 小球-柱形孔运动转换机构
小球-柱形孔运动转换机构存在两处偏心:一是小球球心偏离电机轴线e0;二是小球球心偏离阀芯轴线h0,如图2所示,建立图示坐标系。电机绕轴线Y的旋转运动通过该转换机构传递给阀芯,使阀芯产生两个方向的运动:一是沿X轴线的水平运动xv;二是绕X轴线的转动βv。
由于该压力伺服阀阀芯位移较小(最大值仅为0.1 mm),所需的电机转动角度α也较小(小于6°),则有sinα=α,cosα=1-α2/2,驱动接口运动学方程可以简化为
xv=e0sinα≈e0α
(4)
式中:αx为马达转子的任意工作点;kβv为阀芯绕轴线的转角变化系数。
电机所受的阻力矩为

图2 运动转换机构示意图Fig.2 Structure diagram of movement conversion mechanism
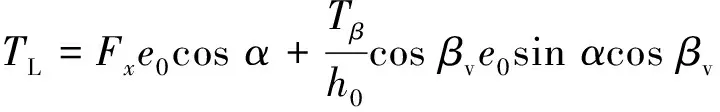
(5)
式中:Fx为小球对阀芯X方向的作用力;Tβ为小球对阀芯绕轴线转动的力矩。
1.2.3 正开口滑阀
由图1可知,滑阀采用二阀肩三通的正开口结构。正常工作时,进、回油口处同时节流,以控制位于进、回油口中间的控制腔中的压力,由阀腔内液体流动的连续性可得控制压力随阀口开度变化的表达式为
(6)
式中:Cd为流量系数;W为节流窗口面积梯度,W=πD;D为阀肩直径;ps为系统压力;pL为整阀控制压力;U为正开口滑阀预开口量;ρ为油液密度;V为负载容腔体积;E为油液体积弹性模量。
在负载容腔体积较小(10 mL)时,忽略油液可压缩性,则控制压力与阀芯位移的关系可表示为
(7)
在任意工作点线性化可表示为
pL=kpxv
(8)
式中:kp为控制压力增益系数。
阀芯在运动过程中受驱动力、稳态液动力作用,正开口滑阀稳态液动力可表示为
Fs=2CvCdWcosθ[xv(ps-pL)-(U-xv)pL]
(9)
式中:Cv为流速系数;θ为射流角。
稳态液动力与滑阀开度有关,可将其视为弹性力,由式(7)~式(9),有
(10)
式中:ks为稳态液动力刚度。
正开口滑阀所受驱动力和驱动力矩的表达式为
(11)
式中:m为阀芯质量;Bv为阀芯沿轴线滑动阻尼系数;Jβv为阀芯绕轴线转动的转动惯量;Bβv为阀芯绕轴线转动阻尼系数。
将式(2)~式(11)代入式(1)可得等效在电机转子上的输出力矩与电机转角的关系:
(12)
式中:JM、BM、KM为伺服阀中机械运动部件等效到电机转轴上的转动惯量、阻尼系数和弹性系数。
1.2.4 电子控制电路
将实际输出的控制压力pL与输入指令电流i的偏差信号进行比例kp、积分ki运算(PI),输出电机的控制信号i0。同时小闭环还反馈电机转角α以增加电机刚度,提高系统的抗扰动性能。压力反馈系数及电机转角反馈系数分别为kf1、kf2。
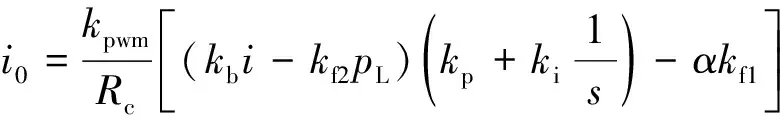
(13)
式中:kpwm为功率放大系数;Rc为电机电阻;kb为指令电流放大系数;s为Laplace算子。
1.3 整阀框图
根据线性化模型式(1)~式(13),可得整阀框图如图3所示。i为伺服阀输入指令信号;ui为调制后的指令信号;u0为输入电机的电压信号。
该阀的动态响应测试结果表明:现有结构和电控方案下,控制压力超调量大,响应调整时间长,即该阀稳定性较差。由整阀框图可知,系统响应与结构参数及PI控制方法均有关系。可通过理论分析获得结构参数及控制方法的影响规律。

图3 BRDDPSV在任意工作点线性化框图Fig.3 Block diagram linearized at any operating point of BRDDPSV
2 结构参数的影响及优化
为分析结构参数对整阀动态特性的影响,去除PI控制器。由框图3可知,整阀的传递函数如式(14)所示:它表示无控制器状态时,输出控制压力和输入电流之间的关系
(14)
式中:ωn为该阀的无阻尼自然频率;ξ为该阀的阻尼比;k为该阀的闭环增益。
2.1 结构参数的影响及优化
根据式(14)可以看出,电机转动惯量、滑阀阀芯质量的增加将导致整阀的惯量增大,会降低系统响应带宽,使整阀响应变慢;而电机力矩系数的增加,提高了整阀的自然频率,降低了阻尼比,整阀动态响应变快。
由式(10)可计算得出不同阀芯直径时的稳态液动力刚度曲线,如图4所示。由计算结果可知,滑阀在运动至全行程的一半附近时,液动力会出现负刚度,不利于阀芯运动的稳定。而减小滑阀直径可以有效减小系统负向的刚度值。因此,选择小直径的阀芯利于削弱液动力对系统稳定性的影响。
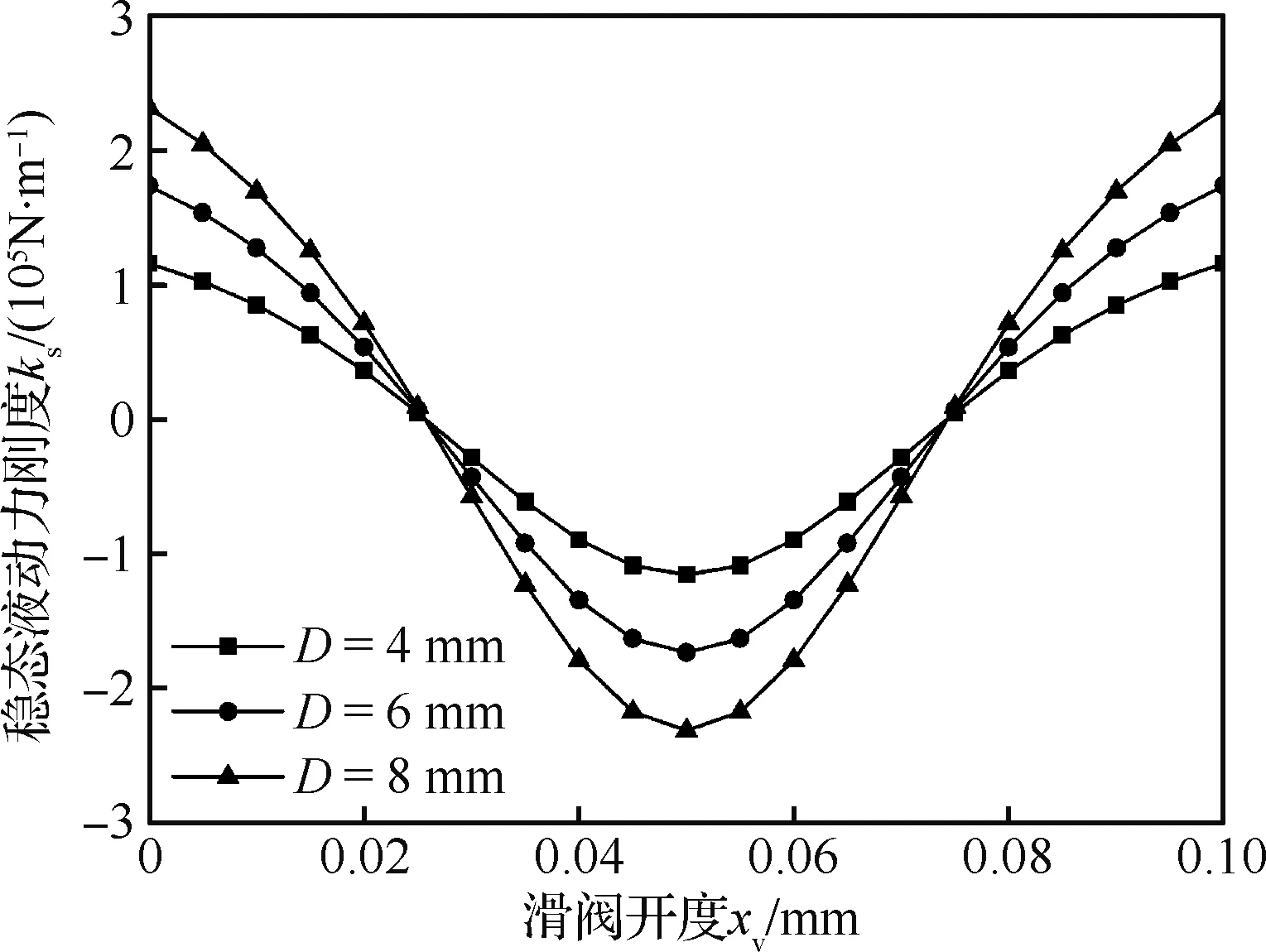
图4 阀芯直径对稳态液动力刚度的影响Fig.4 Effect of spool diameter on steady flow force stiffness
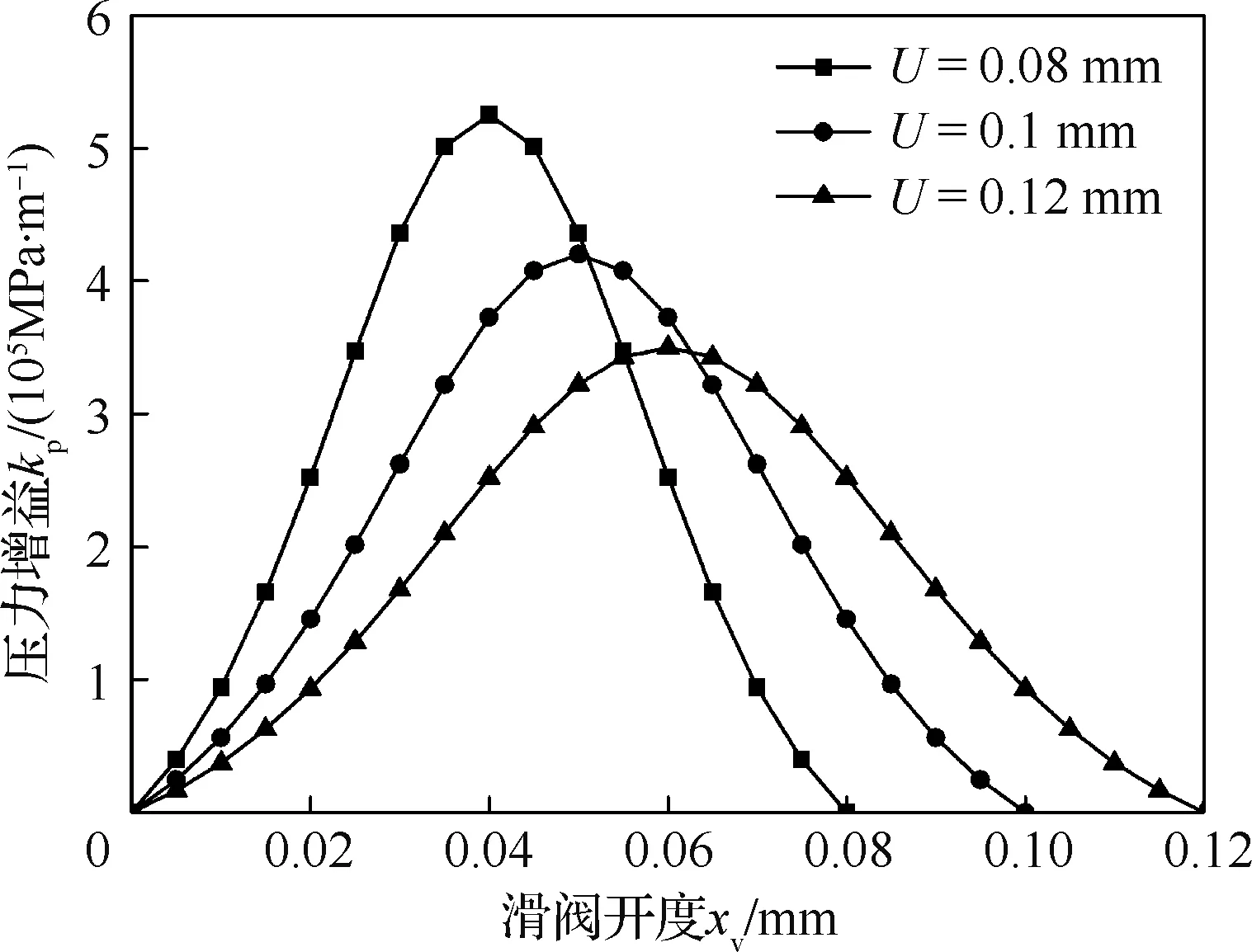
图5 滑阀预遮盖量对压力增益的影响Fig.5 Effect of sliding valve pre-cover on pressure gain
压力伺服阀采用正开口滑阀结构,负遮盖量的大小直接影响滑阀的压力增益kp,如图5所示。从图5中可以看出,压力增益kp随阀口负遮盖量的减小而增大。根据式(14)可知,压力增益的增加能够加大整阀的开环增益,提高控制压力响应的速度,利于改善整阀的响应性能。因此,在条件允许下应尽量减小正开口滑阀的负遮盖量。
2.2 驱动接口的影响及优化
由于安装或加工误差,会造成驱动接口处存在微小的间隙或过盈配合,将造成电机转动过程中的空行程或过大的摩擦力。驱动接口配合偏差如图6所示,间隙量记为Δx。
1) 间隙量Δx>0
Δx>0时,会造成电机转动的一段空行程。则电机空转的最大角度为
(15)
若Δx=0.05 mm,则Δα=2.05°(e0=1.4 mm)电机转角产生了2.05°的死区。
由于电机转角的死区,造成了旋转直驱阀动态特性的改变,如图7所示,为Δx>0时的整阀动态特性。
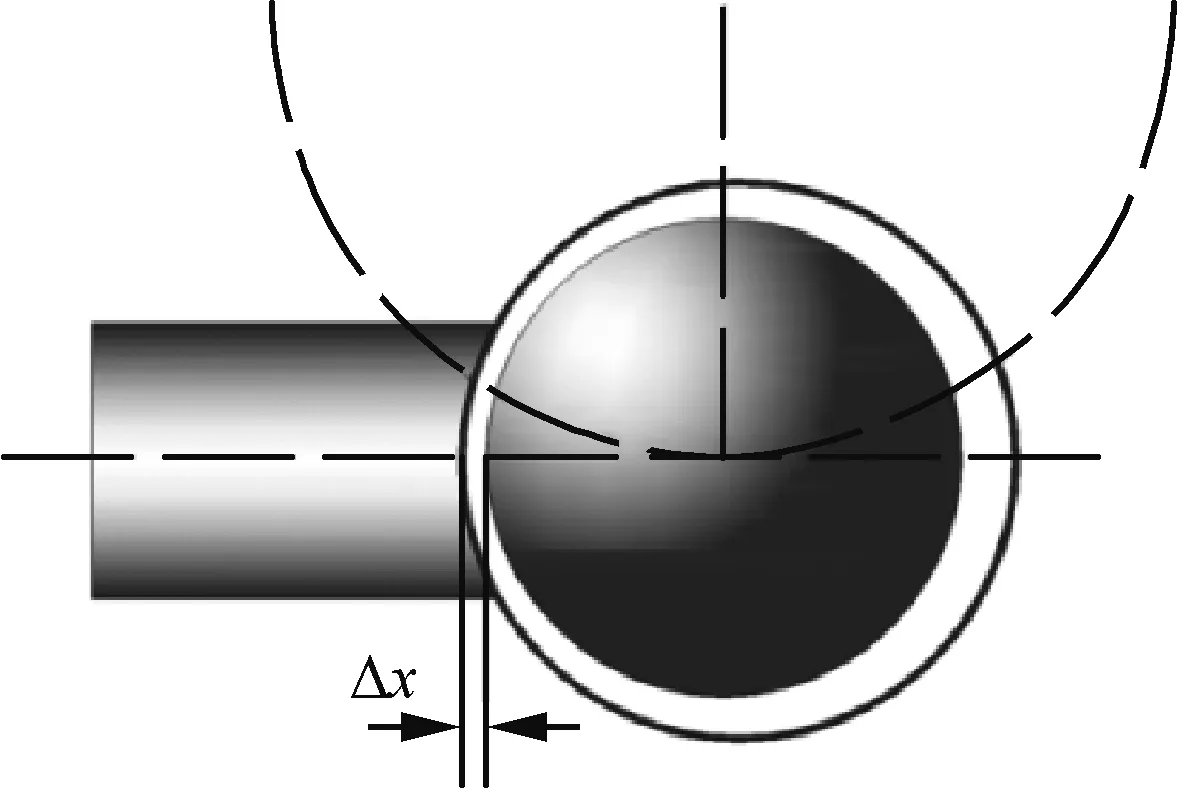
图6 驱动接口配合偏差Fig.6 Deviation of driven interface
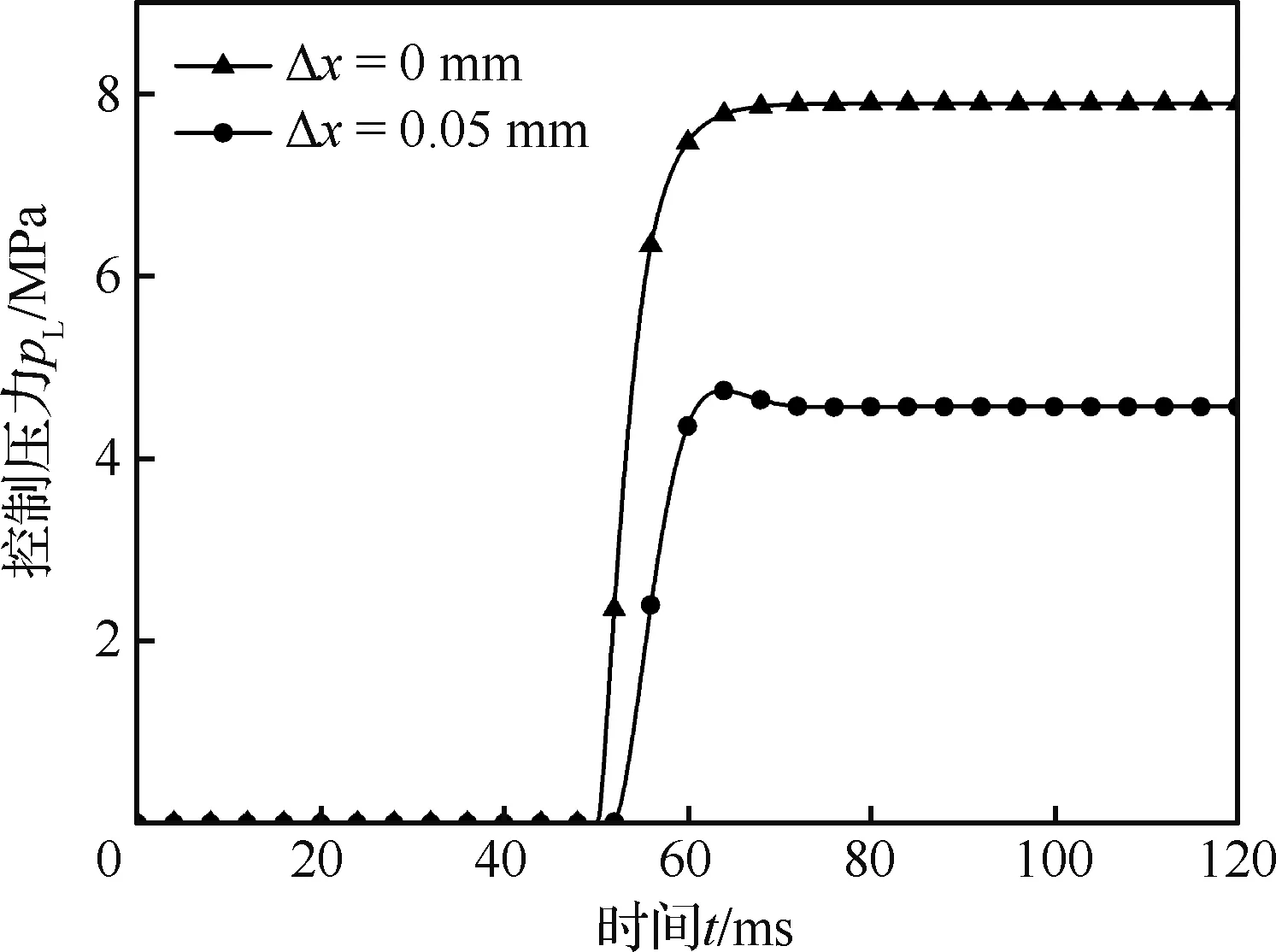
图7 Δx>0时的整阀动态特性Fig.7 Valve dynamics at Δx> 0
可见,驱动接口处的间隙会造成旋转直驱阀的上升过程死区增大,同时其额定压力从8 MPa降低为4.57 MPa。这是由于接口处的间隙造成工作过程中实际推动阀芯的电机转角减小,导致滑阀驱动力下降,从而造成滑阀位移减小,旋转直驱阀的控制压力降低。此外,在驱动小球越过间隙后,会以一定的速度与柱形孔相碰,将使整阀稳定性下降,如图7中间隙为0.05 mm的阶跃响应曲线所示。
2) 间隙量Δx<0
Δx<0表示驱动接口处存在较大的应力和摩擦力。这里假设摩擦力为常数,设摩擦力产生的阻力矩Tf′=0.01 N·m。如图8所示为摩擦力矩对旋转直驱阀动态特性的影响。与正间隙不同,当存在摩擦力时,阀在阶跃响应时不存在死区。这是由于在这种情况下,驱动小球仍然与柱形孔壁接触,电机不存在空转。仅仅由于阻力矩增加,驱动力相对不足,稳态值发生了变化。
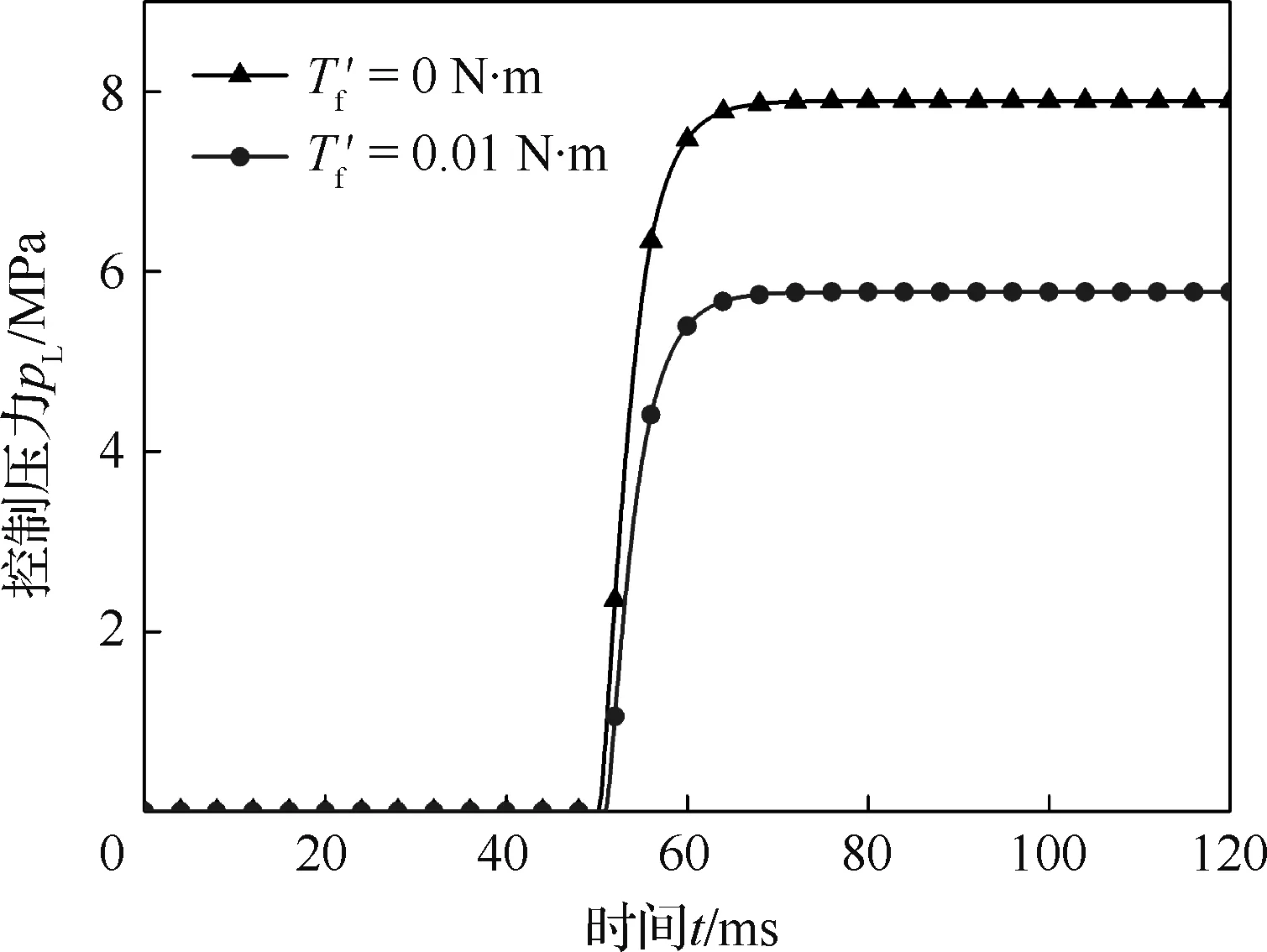
图8 摩擦力矩对整阀动态特性的影响Fig.8 Effect of frictional torque on dynamic characteristics of valve
由于稳态值的静差可通过积分作用消除,通过分析可知,驱动接口处的间隙容易引发阀芯运动的不稳定,因此,驱动接口处应选择小过盈配合,即Δx<0。
2.3 控制策略的优化
旋转直驱电液压力伺服阀通过电机旋转带动滑阀平动,从而实现压力控制。控制策略和控制参数的选择是否合理将直接决定旋转直驱伺服阀动态特性是否符合使用预期要求。
2.3.1 积分分离处理
PID控制器中的积分环节的作用是消除稳态值的静差,保证系统输出的精度。但对于飞机刹车系统中压力控制伺服而言,在启动、停止或大幅度增减设定值时,系统在短时间内输出有很大的偏差,积分环节的累积作用会使系统控制压力出现大幅变化,即表现出超调量大的特征。因此,考虑采用积分分离式PI控制,如图9所示为旋转直驱伺服阀的控制框图。
积分分离可认为是在积分运算前添加开关环节,在指定阈值条件时启动或关闭积分运算[21]。其主要作用是当输入值变化量较大时,即系统输入的指令值与系统实际输出值的偏差大于该积分分离阈值时放弃积分,反之,进行积分消除静差。设e(k)为偏差值,ε为阈值(ε>0),则积分分离可用分段函数表示,β为积分项前的系数:
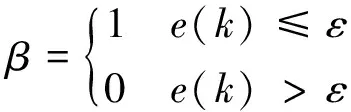
(16)
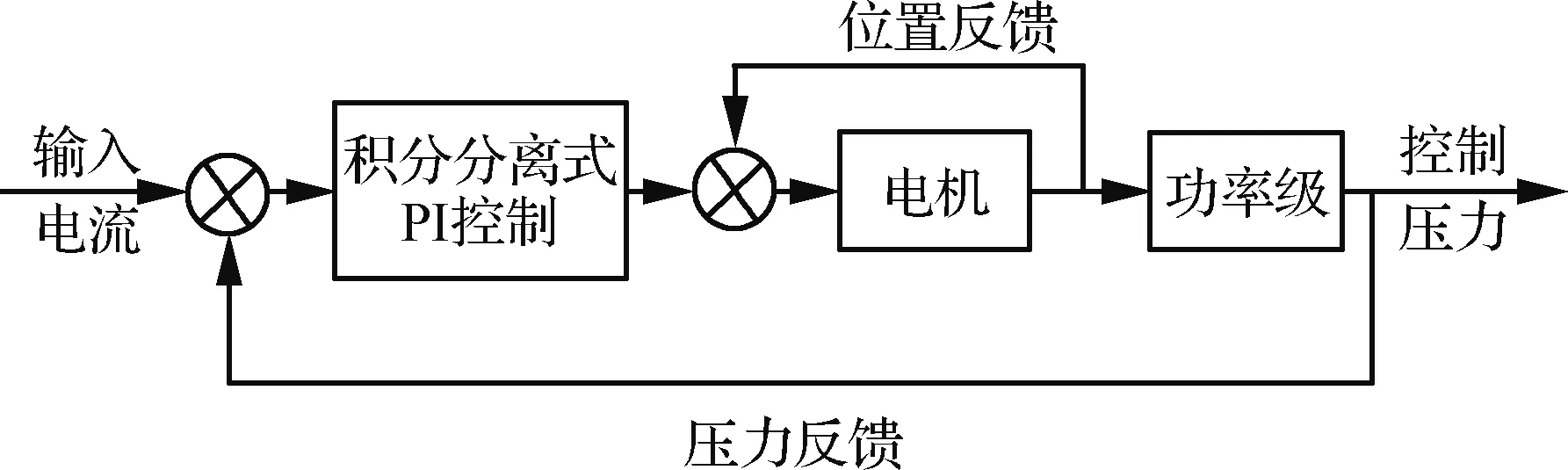
图9 电反馈控制框图Fig.9 Block diagram of electric feedback control
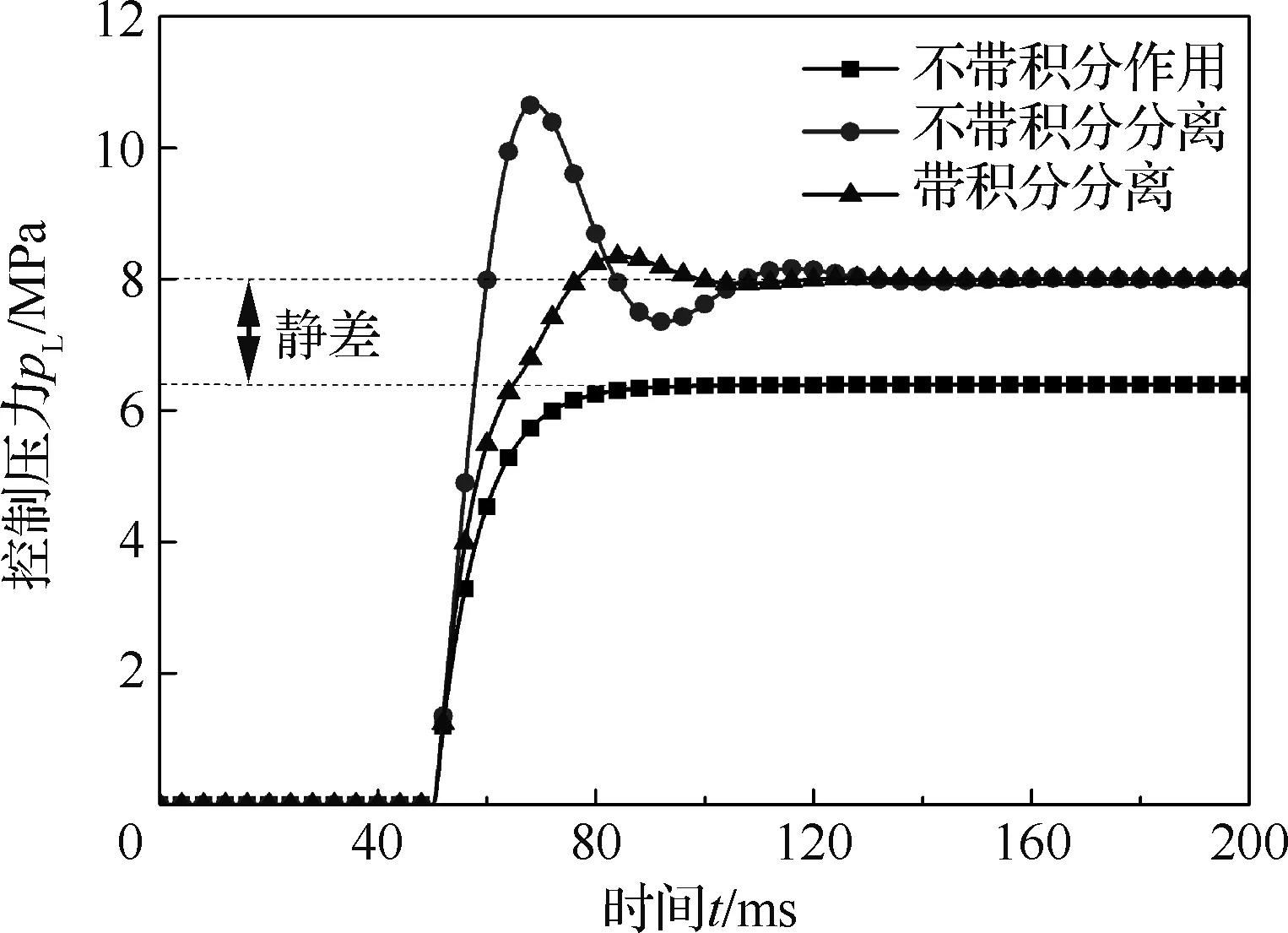
图10 带与不带积分分离的阶跃响应曲线(ε=2 mV)Fig.10 Curve of step response with and without integral separation (ε=2 mV)
将上述积分分离式PI控制器加入仿真模型中,可得图10所示的阶跃输入情况下RDDPV伺服阀动态响应。从图10中可以看出,无积分作用时,稳态值偏离设定值,静差无法消除;持续积分作用时,虽然稳态值无静差,响应速度较快,但会有较大的压力超调。采用积分分离后,合理的积分阈值可以使控制器在压力超调处停止积分,避免控制压力的大幅持续增加,同时达到消除稳态值的静差的目的。
2.3.2 设置动压反馈
为了缩短动态响应的调整时间,考虑增设动压反馈校正来进一步增大RDDPV伺服阀的阻尼,以提高系统稳定性。如图11所示的电控框图,在控制压力的反馈环节并联加入了控制压力的微分项(du/dt)。
动压反馈的输入为压力传感器的采集信号UpL,反馈至输入端之后,其传递函数为
G=kf3s
(17)
因此,压力传感器的输出电压修正为
UpL=kf2(1+kf3s)pL
(18)
式中:kf3为动压反馈系数。
将上述动压反馈模型加入所建仿真模型中,可得图12所示的阶跃输入情况下RDDPV伺服阀的动态响应。可见,动压反馈将控制压力的变化率进行反馈,避免了控制压力的大幅波动,有效缩短了系统响应的调整时间,提高了系统的稳定性。
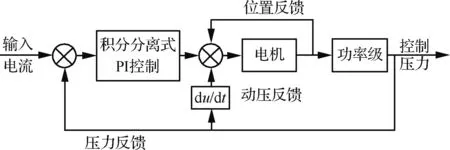
图11 采用动压反馈校正的电控框图Fig.11 Block diagram of electric feedback control with dynamic pressure correction
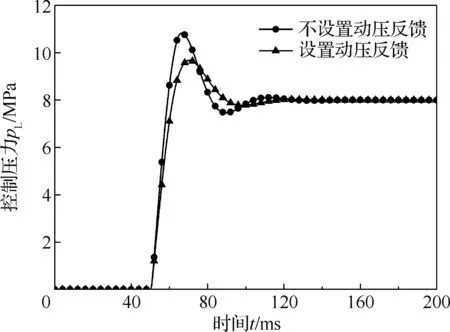
图12 带与不带动压反馈的阶跃响应曲线(kf3=0.000 5 mV·MPa/s)Fig.12 Curve of step response with and without dynamic pressure correction (kf3=0.000 5 mV·MPa/s)
3 优化验证实验
3.1 半物理实验台及实验环境
为免去调试电控参数时频繁搭建模拟电路的繁琐过程,本实验采用半物理仿真平台进行。所谓的半物理即实验台架采用硬件结构,而电控部分采用软件编写。旋转直驱压力伺服阀测试台架如图13所示。图13中右侧的性能测试设备包括测试PC机和信号发生器,内置伺服阀动态特性测试软件;左侧的数字控制PC为便携式笔记本;控制PC机通过信号采集、输出及放大设备与伺服阀和信号发生器相连。测试时输入3.2 mA的阶跃电流信号。采用15#液压油,介质温度为25 ℃±1 ℃。

图13 BRDDPSV测试台架Fig.13 Test bench of BRDDPSV
3.2 动态特性测试结果
根据结构和控制策略的分析,优化后的参数选取如表1所示。电控参数在半物理仿真平台上进行调试获得。
根据表1中优化后的结构和电控参数进行阶跃响应的实验曲线如图14所示,阶跃响应动态指标如表2所示。可见,该阀为欠阻尼系统,优化前,整阀开启时的响应超调量大(超调量约为25%稳态值)、调整时间较长(约75 ms),稳定性较差。优化后,控制压力阶跃响应的超调量明显降低,约为6.25%稳态值,调整时间缩至30 ms左右。虽然控制压力阶跃响应的上升时间有所增加,但可以控制在20 ms以内,基本可以满足飞机刹车压力控制阀的使用需求。
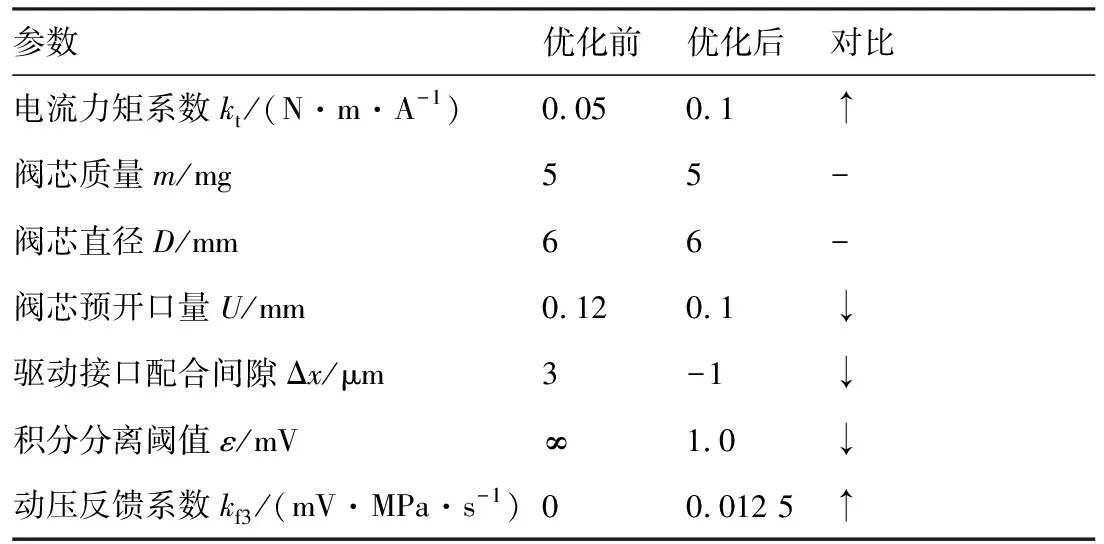
表1 BRDDPSV的优化参数Table 1 Optimization parameters of BRDDPSV
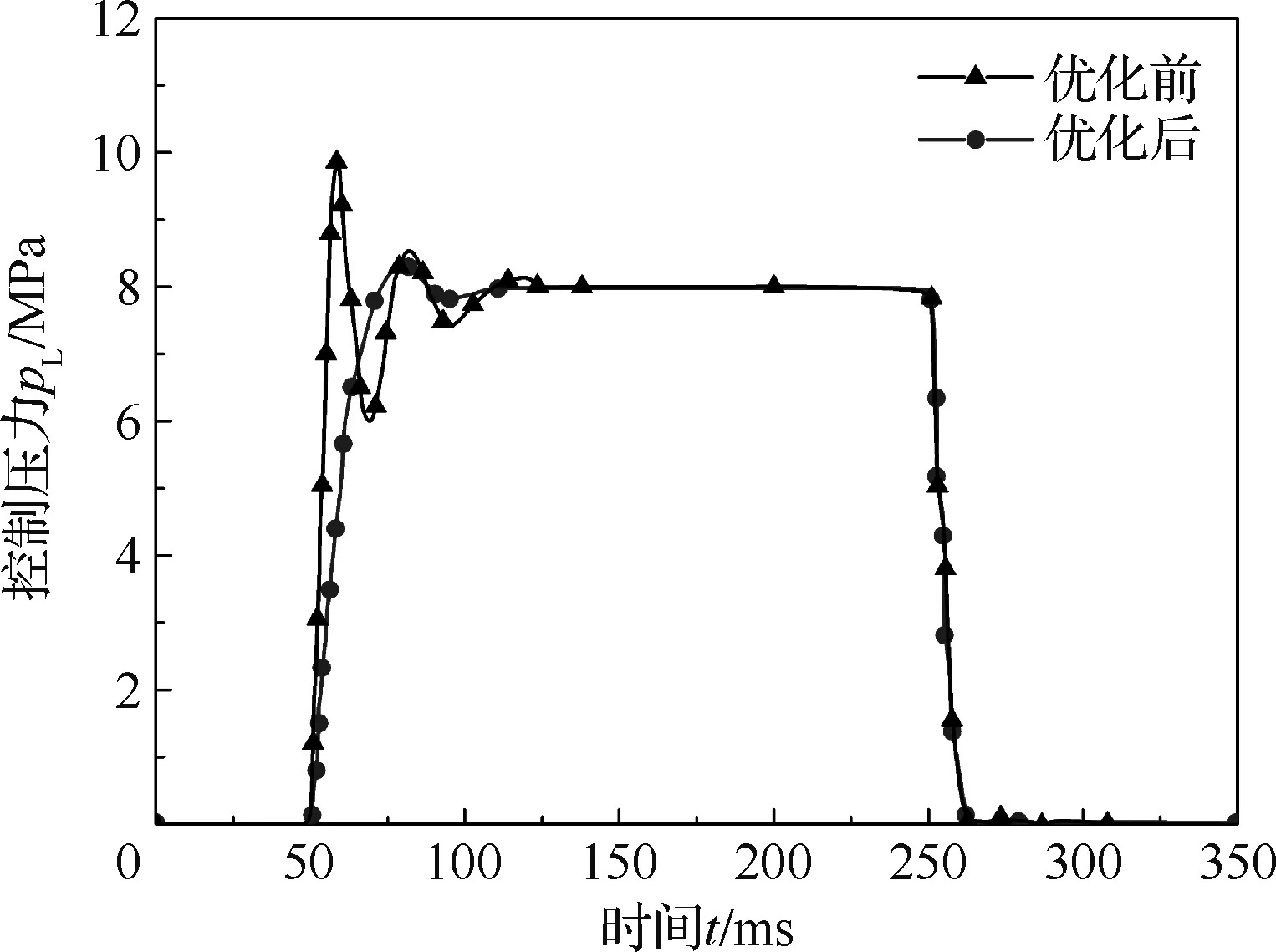
图14 优化前后BRDDPSV的阶跃响应(实验)Fig.14 Step response of BRDDPSV before and after optimization (experiment)
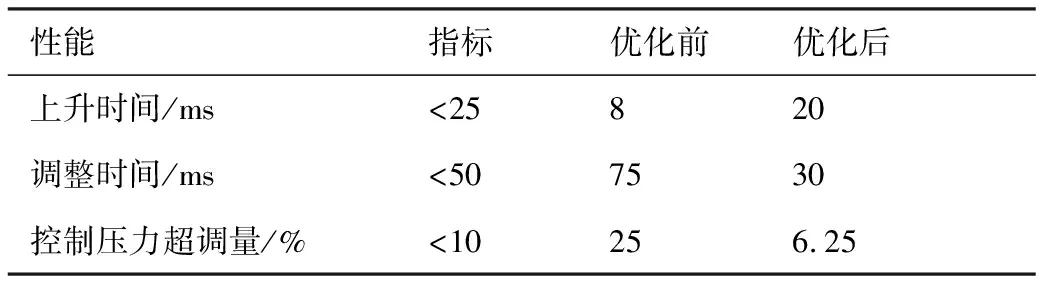
性能指标优化前优化后上升时间/ms<25820调整时间/ms<507530控制压力超调量/%<10256.25
4 结 论
1) 提高整阀响应稳定性和可靠性的措施:消除整阀负刚度,包括减小阀口负遮盖量以提高压力增益,减小阀芯直径以减小最大负刚度值;提高电机抗干扰能力,如提高电机电流-力矩系数,及在驱动接口处小球和柱形孔间采用小过盈配合。
2) 优化控制方法:采用积分分离式的控制器。理论和实验表明,适当的积分分离阈值可以有效降低控制压力超调值,使整阀响应趋于稳定;设置动压反馈校正。将控制压力的变化率反馈到输入端进行控制,这相当于在系统中增加了阻尼,整阀的阶跃响应调整时间明显缩短。整阀的上升时间稍有加大,但可以控制到20 ms以内。

