基于前体激波的内转式进气道一体化设计

乔文友，余安远，杨大伟，乐嘉陵2,

1. 西南科技大学 燃烧空气动力学研究中心，绵阳 621010 2. 中国空气动力研究与发展中心 高超声速冲压发动机技术重点实验室，绵阳 621000 3. 中国空气动力研究与发展中心 吸气式高超声速技术研究中心，绵阳 621000

近十几年来，高超声速飞行器的设计已经成为航空航天领域的一个热点，前体/进气道的一体化设计是其中的关键[1-2]。高超声速飞行器的一体化设计分别对飞行器前体和进气道提出了更高的要求[3]。对飞行器前体而言，不但要为进气道提供高品质的预压缩流场，还应确保进气道捕获足够的流量。相对于传统的升力体结构，乘波前体可以抑制两侧来流，因而不但具有较高的升阻比，而且还可控制来流的横向偏转角，目前已经成为高超声速飞行器设计领域一个主要的研究方向[4-5]。对于进气道来说，在对来流进行高效压缩的同时还应满足结构形状、作用力矩及热防护等要求。目前，内转式进气道由于其优越的气动性能，在吸气式高超声速推进系统设计中的应用越来越广泛。

在腹部进气的一体化设计中，由于内转式进气道入射激波曲面一般为三维内收缩锥形状，这使得进气道唇口与飞行器前体激波很难贴合，进而带来较大的流量损失。此外，内转式进气道对来流的均匀性要求较高，进一步加大了内转式进气道与飞行器前体进行一体化设计的难度。如HSSW和SR72的前体两侧存在较大的溢流，严重影响了进气道的流量捕获系数。因此，采用现有内转式进气道设计方法很难将内转式进气道的唇口型线与前体激波匹配起来，从而影响进气道的流量捕获系数。这是因为在设计过程中，如果根据捕获截面形状在入射激波中截取进气道唇口型线，几乎无法使进气道唇口型线贴近前体激波曲面；反之，如果采用进气道入射激波与前体激波相惯的方式确定进气道的唇口型线，则很难有效控制进气道的捕获截面形状和尺寸，进而难以控制进气道的捕获流量。

对于腹部进气的一体化设计构型，目前普遍采用的设计方案主要有：① 优化前体的一体化设计[6-9]，主要针对前体进行优化使进气道入口附近流场尽可能均匀，这类设计方案应用最为广泛;② 飞 行器前体与进气道共用基本流场的腹部进气方式，如贺旭照[10]和尤延铖[11]等提出的一体化构型；③ 直接在非均匀来流上设计内转式进气道的一体化设计方法，主要有澳大利亚昆士兰大学Smart团队[12]。这些方案中，前两种对前体约束较多，设计灵活性较低；第3种方案虽然关注了进气道唇口型线与前体激波的关系，但很难同时兼顾高流量捕获与捕获截面形状可控的矛盾。为降低内转式进气道与飞行器前体一体化设计时的流量损失，并在设计过程中有效控制进气道的捕获截面的形状，需要发展一种新型的内转式进气道一体化设计方法。

本文针对这一问题发展了一种基于前体激波的乘波前体/内转式进气道一体化设计方法，通过调整入射激波形状，使捕获截面形状和进气道唇口型线能够与前体激波实现较好匹配，同时兼顾高流量捕获与捕获截面形状可控，并对该进气道的气动性能和流动特征进行数值研究。

1 入射激波形状和沿程马赫数可控的基本流场设计

目前内转式进气道大都采用吻切流方法设计，其中基本流场对进气道的气动性能起着决定性的作用。经过最近十几年的研究，内转式进气道的基本流场已经从开始的Busemann流场发展到性能更加优越的弯曲入射激波基本流场。南京航空航天大学张堃元团队[13-15]对内转式进气道基本流场开展了比较深入的研究，提出了沿程压力/马赫数分布可控的基本流场设计方法，使进气道的气动性能得到较大提升。厦门大学尤延铖团队[16-17]在此基础上还进一步发展了特征线-流线的流场推进方式，拓展了基本流场的设计方法。这些基本流场设计方法均是通过调节压缩面的沿程参数(指定压缩面形状或压力/马赫数分布规律)来确定入射激波的，在一体化设计中便会面临前面所述的问题。

为拓展内转式进气道与前体匹配的灵活性，本文通过给定的入射激波形状和沿程马赫数分布设计基本流场，设计原理如图1所示。具体设计步骤为：① 给定入射激波AF的形状，然后应用逆特征线法[18-19]求解入射激波波后依赖域ABF的流场；② 将入射激波AF的波后依赖域ABF的出口BF作为等熵压缩段的入口，给定压缩面BC的沿程马赫数分布，应用特征线法确定等熵压缩段区域BCF的流场参数；③ 给定中心体FD的变化规律，以等熵压缩段BCF的流场参数作为来流条件，应用特征线法求解反射激波CF的形状以及整流区域CDF的流场参数分布。根据该方法的原理可知，应用该方法可通过调节入射激波形状，使捕获截面与前体激波能够较好匹配。

2 可匹配前体激波形状的内转式进气道设计方法

本文针对典型的乘波前体，设计与前体激波能够较好匹配的内转式进气道。进气道的整个设计过程,尤其入射激波形状的设计需要基于前体激波形状进行。在设计过程中还需给定捕获截面形状以增强内转式进气道设计方法的灵活性。具体设计包括前体激波确定和与前体匹配的内转式进气道设计两方面。

2.1 前体激波确定

本文采用与法国JAPHAR计划飞行器[20]类似的乘波前体，并在前缘设置直径为4 mm的钝化前缘。用ICEM软件生成计算网格，为确保前体激波形状准确性，计算网格量约为1 500万。计算来流条件为海拔30 km的高空，飞行马赫数为7.0；应用商业软件Fluent求解该前体的流场结构，对流通量采用二阶迎风Roe格式，气体参数采用分段多项式拟合，黏性系数采用Sutherland公式计算，湍流模型采用Re-Normalization Group (RNG)k-ε模型，壁面为绝热固壁，近壁边界采用非平衡壁面函数处理，边界网格加密确保壁面附近第1层网格y+<10，计算域进出口分别采用压力远场和压力出口边界条件。本文采用的计算方法已经在文献[21]中进行了验证，结果表明该方法完全可以模拟内转式进气道中的流动现象。前体构型及数值模拟结果如图2所示，图中Ma为马赫数，VX、VY、VZ为X、Y、Z3个方向的速度分量，图2(b)中等X截面左侧为纵向偏转角(arctan(VY/VX))等值线图，右侧为横向偏转角(arctan(VZ/VX))等值线图。

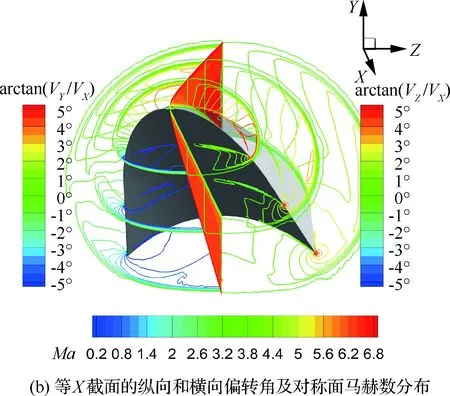
图2 乘波前体的数值模拟结果Fig.2 Results of numerical simulation of waverider forebody

由图2(a)可知，受钝化前缘影响，前体激波脱体。前体下方气流的均匀性如图2(b)所示，气流的纵向偏转角基本上都在4.3°左右；钝化前缘处的横向偏转角大于2°，主流区域大都分布在0°～1° 之间。综合分析前体下方气流的偏转角分布发现，纵向偏转角分布比较均匀，在设计过程中只需对此调节进气道基本流场的轴线方向；横向偏转角的影响仅局限于前缘附近区域，设计中对此不做特殊处理。

综合分析图2的计算结果可知，虽然给定前体的流场无法实现全流量捕获，但流场的均匀性较好，仍然可与内转式进气道进行一体化设计。因此，本文的内转式进气道将基于该前体激波形状进行，忽略来流均匀性的影响。

2.2 与前体匹配的内转式进气道设计

内转式进气道的设计采用吻切流方法进行，基本流场的设计则是整个进气道设计方法的核心，设计步骤如下：

1) 确定可全流量捕获的进气道唇口型线(Inlet Full Capture Curve, IFCC)

给定捕获截面形状如图3所示，其边界可分为前体捕获流管曲线(Flow Capture Tube, FCT)和进气道捕获型线(Inlet Capture Curve, ICC)。其中，FCT由前体前缘线决定，ICC则根据设计需求给定。这两者交点顺来流方向投影至前缘上的点为上唇罩点。本文给定ICC的表达式为

y=a1+b1z+c1z2+d1z3+e1z4z∈[-1,1]

(1)

式中：a1、b1、c1、d1和e1均为无量纲系数，给定a1=1，b1=1.367 80×10-13，c1=4.276 04×10-1，d1=-2.580 16×10-13，e1=5.723 95×10-1。

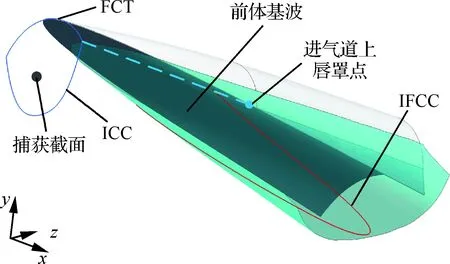
图3 可全流量捕获的进气道唇口型线Fig.3 Inlet full capture curve

将ICC分别沿y方向和z方向等比例缩放至捕获截面实际尺寸，然后顺来流方向投影至前体激波曲面(如图2(a))上得到IFCC，如图3所示。由此可知，当前体完全乘波时，IFCC便与前体前缘线相交，从而以确保进气道实现全流量捕获。

2) 确定进气道基本流场入射激波形状

将前体激波下游主流方向作为基本流场中心体轴线的方向，将整个前体绕z轴旋转4.3°，使基本流场前方来流基本保持水平方向。根据IFCC和中心体半径确定中心体轴线的纵向位置，将IFCC绕中心体轴线旋转得到一个回转曲面，该曲面的子午线即为可实现全流量捕获的入射激波(Inlet Full Capture Incident Shock, IFCIS)，如图4(a)所示。也就是说，IFCIS为理论上可实现全流量捕获的入射激波形状。

将中心体轴线与y轴所在平面定为一个基本平面，并将上唇罩点在中心体轴线的垂点作为基本流场的原点。在改平面内，基于中心体轴线、原点以及过原点与轴线垂直的坐标轴构造基本流场的相对坐标系。整个基本流场的设计均在相对坐标系内完成，设计进气道时只需将在基本流场内追踪的流场还原至绝对坐标系即可。

将上唇罩点绕中心体轴线旋转至基本平面确定基本流场入射激波的起始点，如图4(b)所示，图中R为径向。由图4(b)可知，由于前体并未完全乘波，使得进气道上唇罩点与IFCC存在一定距离。因此，在实际中进气道无法实现全流量捕获。为确保进气道具有较高的流量捕获能力，应在用吻切流方法设计内转式进气道时，在确保入射激波物理上存在的前提下尽可能靠近IFCIS。本文给定入射激波形状表达式为

y=a2+b2x+c2x2+d2x3

(2)

式中：a2、b2、c2和d2为系数。然而，激波存在性问题在数学上还没有被证明，因此在设计中还需根据激波波后依赖域的特征线网格进行迭代。

为检验本文方法的效果，给出了两条入射激波IS-1和IS-2。其中，IS-1为尽可能靠近IFCIS的入射激波，用以检验进气道波系匹配的效果。由发动机原理可知，进气道的捕获流量对发动机的推力至关重要。进气道唇口前突至前体激波上游虽然可以有效提升捕获流量，但前体激波与进气道唇口处入射激波之间的相互干扰对总压恢复系数会产生一定影响。为进一步分析这两道激波之间的相互干扰对气动性能的影响，本文设计了入射激波IS-2。该激波中部略微前突至IFCIS上游，从而使进气道唇口略微前突至前体激波上游。这两道激波的设计参数分别为

图4 基本流场入射激波的设计原理图Fig.4 Design schematic of incident shock in basic flow field

IS-1：a2=1，b2=-2.213 60×10-1，c2=2.702 94 ×10-2，d2=-6.892 41×10-3。

IS-2：a2=1，b2=-2.315 15×10-1，c2=1.694 69×10-2，d2=-4.964 63×10-3。

3) 求解基本流场

基本流场的求解原理如图1所示：由前体激波下游的流场参数确定基本流场的来流马赫数为6.21，然后应用激波关系式根据给定的入射激波形状确定波后流场参数，再应用逆特征线法[18-19]求解入射激波的波后依赖域流场，最后结合压缩面的沿程马赫数分布和下边界形状求解整个基本流场的参数分布。

压缩面的沿程马赫数分布采用三次样条控制，控制参数如图5(a)所示。图中xs、Mas、θs与xe、Mae、θe分别为压缩面的起始点(图1中点B)和压缩面的末端控制点(图1中点C)处的轴向位置、马赫数和切线的倾角，xm和Mam为样条曲线中部控制点的轴向位置和马赫数。其中，起始位置参数由给定的入射激波形状控制，其余参数需要根据设计要求给定。基本流场下边界FD的给定采用分段函数，其表达式为

(3)

式中：ξ=x-xF，xF为进气道下唇罩点(图1中的点F)的轴向位置；L为控制长度；a3、b3和c3为三次多项式的系数；RF和RL分别为点F处和xF+L处的中心体半径。

为便于对应用IS-1和IS-2两种激波形状设计的进气道对比，本文给定相同的沿程马赫数分布和下边界形状。具体的设计参数为

压缩面：tanθs=0.2、xe= 5.2，Mae=4.3，tanθe=0.3，xm=0.7xs+0.3xe，Mam=0.6Mas+0.4Mae。

下边界：a3=0.179 98，b3=-0.197 85，c3=-2.9×10-3，L=0.8，RF=9.612 62×10-2，RL=0.4RF。

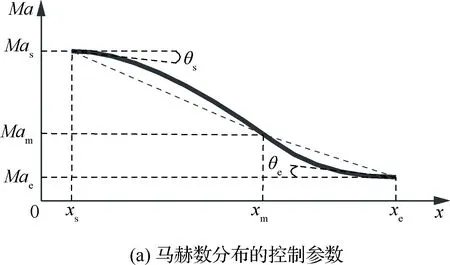
图5 基本流场压缩边界的沿程马赫数分布曲线和马赫数分布云图Fig.5 Curve of Mach number distribution along compression boundary and contours of Mach number of basic flow field

应用特征线法求解得到基本流场如图5(b)所示，基本流场的总体性能如表1所示。表中CR为总收缩比，ICR为内收缩比，Mae、πe和σe分别为基本流场出口的马赫数、压比和总压恢复系数。结合本文基本流场的设计方法可知，入射激波IS-1损失较小，但压缩边界末端马赫数(Mae)相同必然导致反射激波上游等熵压缩所占比重和气流偏转角的上升。在相同的下边界形状下，溢流口处反射激波的强度必然上升，从而使反射激波的损失增大。在入射激波和溢流口处反射激波的共同作用下，两个基本流场出口的总压恢复系数相当。此外，较小的入射激波损失使得收缩比较大，但相同的压缩边界沿程马赫数分布以及下边界形状却使两个基本流场的内收缩比基本一致。

表1 基本流场气动性能Table 1 Aerodynamic performance of basic flow field

4) 生成进气道型面

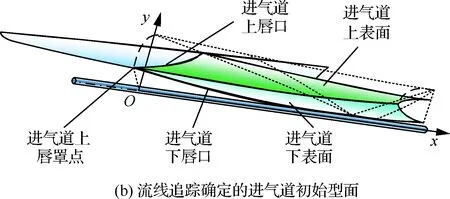
图6 内转式进气道型面的设计原理图Fig.6 Design schematic of inward-turning inlet profile

无黏的进气道型面生成原理如图6所示。首先将基本流场入射激波绕中心体轴线旋转得到入射激波曲面，该曲面与乘波前体在绝对坐标系中的交线即为进气道上唇口，将ICC顺来流方向投影至入射激波曲面得到进气道下唇口；然后，将进气道的上下唇口离散为系列点，并根据这些点与中心体轴线的距离在基本流场中追踪出系列流线，将这些流线偏转至相应的离散点处，得到无黏的进气道型面。

本文给定进气道喉道截面形状为椭圆，其长短轴之比为1.9。因此，在设计过程中需要通过横截面过渡技术进行光顺。本文应用流线融合技术[22]以及黏性修正技术[23]设计喉道截面可控的进气道构型。两个进气道的总收缩比均为10.0，内收缩比分别为1.98和2.03。

一体化设计中，为便于进气道与燃烧室匹配，给定隔离段出口为1.3倍喉道面积的圆，长度约7.0倍的喉道当量半径，出口截面法向与远前方来流一致。给定隔离段对称面处上下边界形状，并应用商业软件UG中的扫掠命令直接生成隔离段的型面。上下边界的设计非本文研究的重点，不再赘述。最终的进气道构型如图6(c)所示。

3 数值模拟

为进行热防护，在进气道唇口位置也设置直径4 mm的钝化前缘，在进气道外围设计唇罩，并通过数值模拟检验本文设计方法的效果。数值模拟采用Fluent软件进行，计算方法与前体流场数值模拟相同。由于模型和流动均为对称结构，在计算过程中取一半模型生成网格计算。用ICEM软件生成总数为880万的结构化网格，壁面附近网格进行加密确保壁面第1层网格y+<10。计算采用来流条件进行初始化，以检验进气道在工作马赫数范围内的气动性能。分别在设计点和不同来流条件下进行数值模拟，检验进气道的气动性能，同时分析进气道唇口与前体激波略微干扰时对气动性能的影响。计算来流条件如表2所示,表中Ma∞为来流马赫数，H为飞行高度，p∞和T∞为来流静压和静温。

3.1 设计点时进气道的气动性能

图7给出了应用入射激波IS-1和IS-2设计的进气道在Ma∞=7.0时的马赫数分布云图。由于进气道钝化前缘的影响，前体激波与唇口附近产生的局部脱体激波相互干扰，使进气道的入射激波无法贴近进气道唇口。然而，进气道对称面处的入射激波依然保持贴口，一方面说明前体下方流场的非均匀性对进气道的影响很小，进而说明该前体和内转式进气道可以进行较好的一体化设计；另一方面说明本文基本流场设计方法和黏性修正技术可有效用于此类前体的一体化设计。

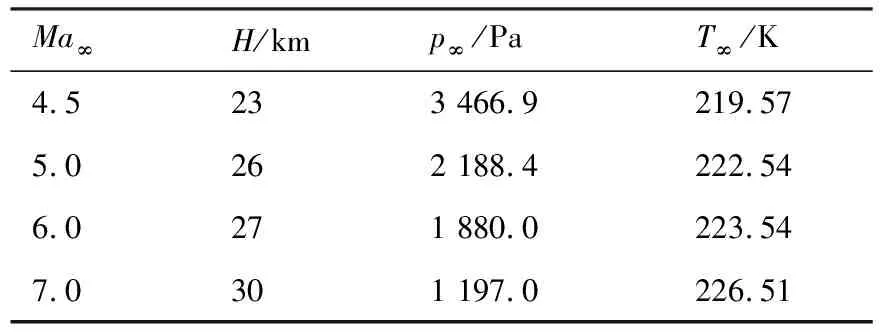
表2 计算来流条件Table 2 Incoming flow conditions of calculation

图7 设计点等X截面和对称面处的马赫数分布云图Fig.7 Mach number contours of X-section and symmetric plane at design point

根据图4(b)中入射激波IS-1、IS-2与IFCIS的关系可知，基于IS-1设计的进气道唇口型线基本处在前体激波下游，而基于IS-2设计的进气道则会有部分唇口前突至前体激波上游。由图7中前体激波与进气道唇口的位置关系可知，进气道的唇口型线与入射激波之间的位置关系基本符合给定的设计条件，说明本文方法可以通过设计入射激波形状以实现进气道与前体的匹配。在钝化前缘的影响下，进气道唇口附近的波系结构已经发生明显变化，因此还需对进气道内部的流场结构以及气动性能做进一步分析。

图8给出了进气道等X截面压力分布云图和极限流线分布，局部放大图分别给出了进气道上唇口附近的压比(π)分布云图和隔离段内等X截面的总压恢复系数(σ)云图。极限流线经过前体激波后基本不发生偏转，与图2中流线偏转角的分布基本一致。根据进气道上唇口附近的压力分布分析可知，由于进气道上唇口向下游“凹进”(如图6(b)和图8所示)产生由两侧至对称面的横向压力梯度，使极限流线向对称面处逐渐偏转。在溢流口发出的反射激波附近，极限流线迅速汇聚并形成较强的流向涡进入隔离段。这是因为溢流口处的反射激波较强，加上此处附面层已经在进气道外压缩段内充分发展，厚度较大，导致激波/附面层干扰强度较大，最终产生了流向涡结构。

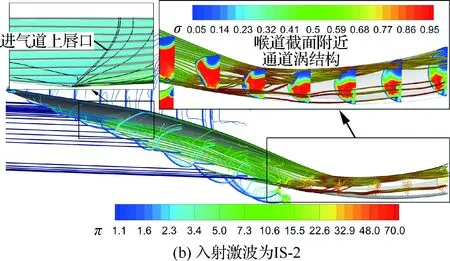
图8 设计点等X截面的压比和总压恢复系数云图及进气道极限流线分布Fig.8 Pressure ratio and total pressure recovery coefficient contours of X-section and limit streamlines of inlet at design point

在隔离段内部，进气道两侧的流向涡逐渐向顶部汇聚，使低能流区域迅速增大。

3.2 进气道的总体气动性能

图9和图10分别给出了不同来流马赫数下，应用入射激波IS-1和IS-2设计的进气道(称为IS-1和IS-2构型)对称面和隔离段出口的马赫数云图。表3给出了相应的气动性能,表中φ为流量捕获系数，Maf、πf、σf和ηKE分别为隔离段出口的马赫数、压比、总压恢复系数和动能效率。从图9、图10和表3可以看出，在两个进气道的流场结构、出口马赫数分布以及流场参数基本一致。这说明，当入射激波形状略有差异时，应用相同的等熵压缩段设计参数得到的进气道流场也基本一致。进一步说明，本文基本流场的设计方法可以灵活控制进气道的压缩规律和压缩程度。

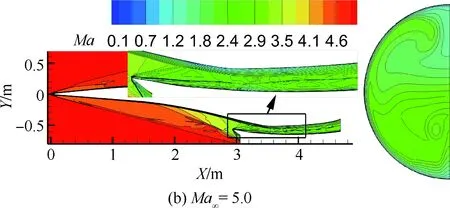
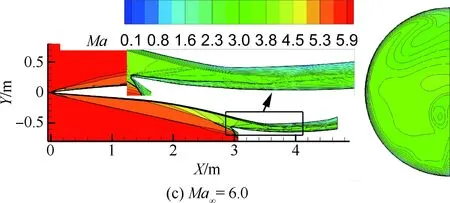
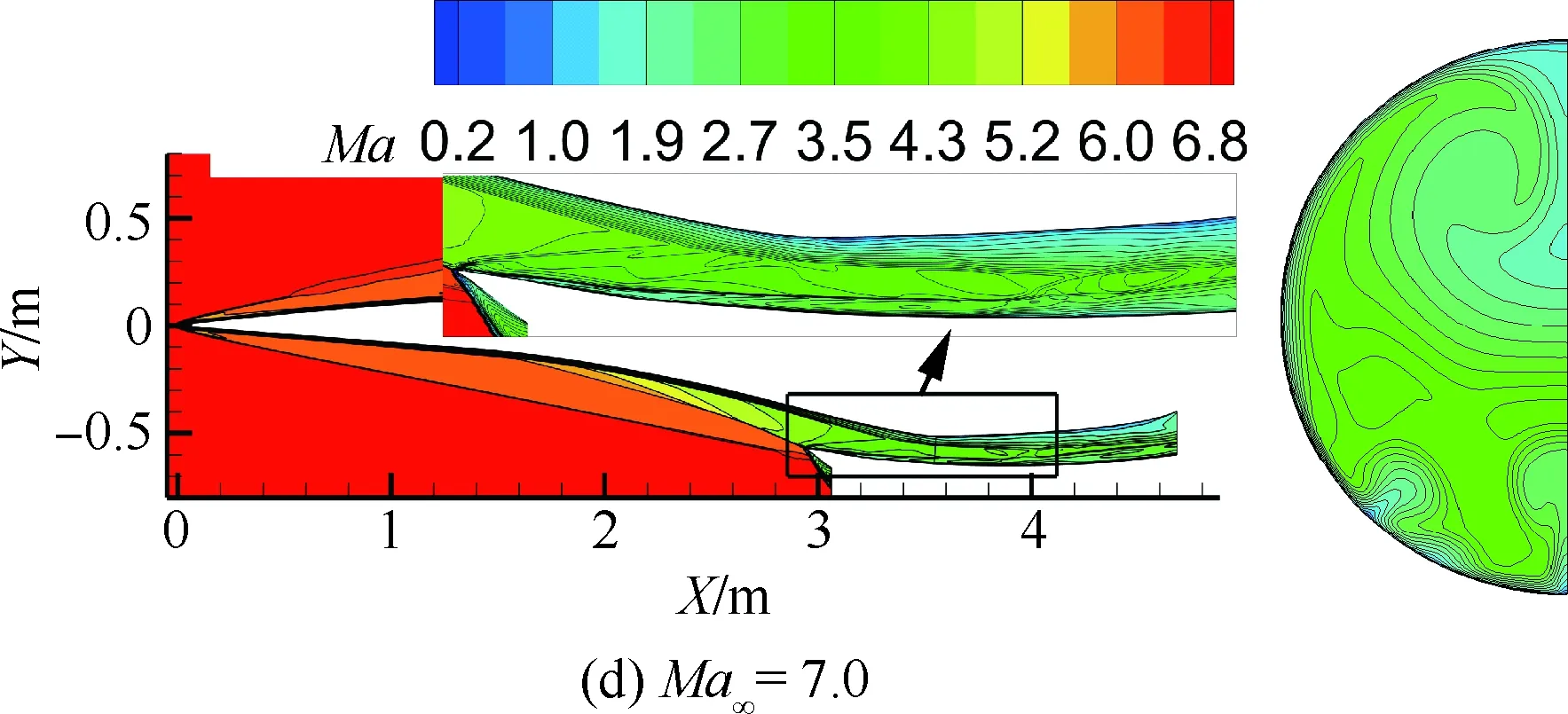
图9 IS-1构型对称面和隔离段出口马赫数云图Fig.9 Mach number contours of symmetric plane and isolator exit section of IS-1 configuration

综合分析图9和图10中的流场结构发现，来流经前体激波和进气道入射激波两级压缩，这两道激波随飞行马赫数的降低逐渐远离进气道唇口，加大了进气道溢流，有利于提升进气道的起动性能。此外，经两级激波压缩的进气道可有效缩短进气道的长度，进而减轻结构重量[24]。

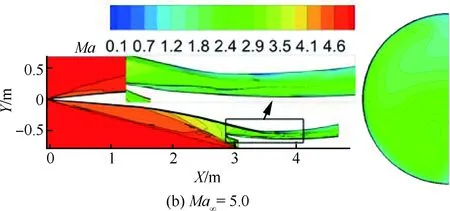
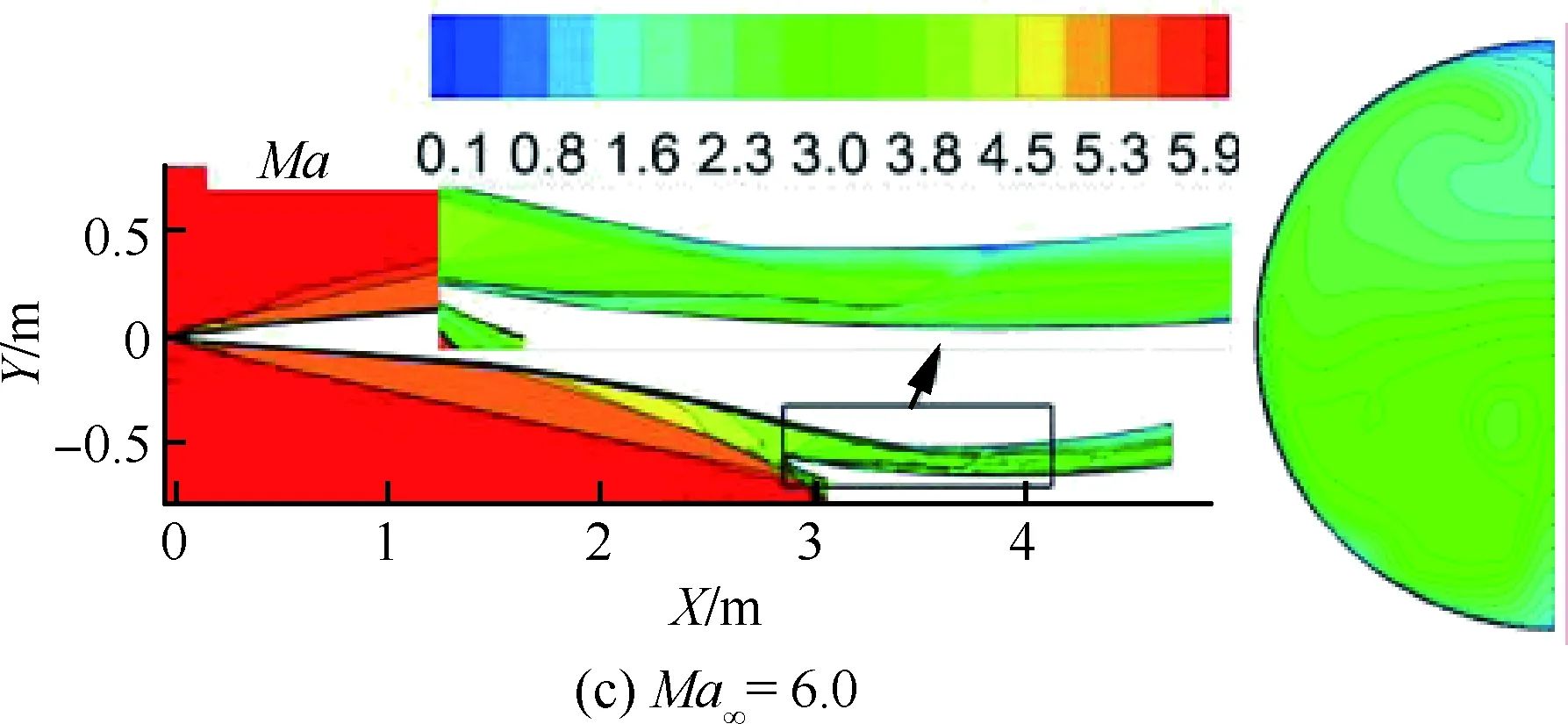
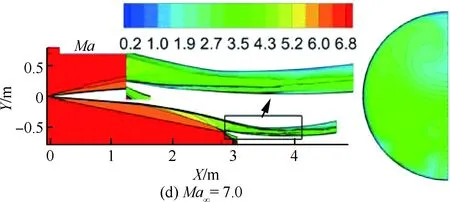
图10 IS-2构型对称面和隔离段出口马赫数云图Fig.10 Mach number contours of symmetric plane and isolator exit section of IS-2 configuration

进气道型面Ma∞φMafπfσfηKEIS-1构型4.50.6842.0521.60.6500.967 7 5.00.7452.2625.60.6020.968 8 6.00.8612.7931.10.5670.975 6 7.00.9623.1640.50.5000.977 7 IS-2构型4.50.7222.0022.60.6400.966 45.00.7762.2522.70.5950.968 06.00.8872.7929.50.5560.974 67.00.9763.1738.90.4870.976 7

隔离段内部的流动结构可结合图8进行分析，进气道溢流口发出的反射激波与附面层相互干扰产生较强的流向涡。在隔离段内，流向涡与上表面的低能流汇聚促使流动损失区域迅速增大，并在出口产生较大的低能流区域。溢流口下游虽然没有较厚的附面层，但是依然产生了较小的流向涡结构。由图8可知，这对流向涡结构的产生过程为：在溢流口附近较小的横向压力梯度作用下，溢流口处钝化前缘产生的低能流只能顺流向进入隔离段；然而在隔离段内部，激波(尤其是肩部发出的二次反射激波)与壁面相交产生了由两侧至对称面的横向压力梯度，进一步与附面层的相互干扰使低能流向对称面处汇聚并产生一对方向相反的流向涡结构。

结合表3中的总压恢复系数σf和动能效率ηKE进行分析可知，当来流马赫数降低时，隔离段内的激波/附面层干扰强度降低，使得隔离段内和出口的流场品质显著提升。

由表3可知，在设计点基于IS-2设计的构型比IS-1构型总压恢复系数σf和动能效率ηKE分别降低2.60%和1.02‰，而流量捕获系数φ则提升1.45%。这是因为入射激波IS-2的中部相对于IS-1略微前移，导致IS-2构型的唇口在基本流场轴向的投影面积增大，相当于增大了进气道的实际捕获面积。换言之，虽然这两个构型的唇口在自由来流方向上的投影面积相同，但受前体预压缩的影响，IS-2构型的唇口在前体预压缩气流方向上的投影面积(也可称为相对前体的捕获截面积)更大。

伴随来流马赫数的降低，IS-2构型的流量捕获系数相对于IS-1构型略有提升，而总压恢复系数和动能效率的损失却相对较小。这说明IS-2构型中前体激波与入射激波的干扰对整个进气道气动性能的影响较小；从捕获流量角度而言，这种设计反而更有利于提升发动机的推力。

由此可知，当进气道唇口略微前突时，前体激波与进气道入射激波的相互干扰未必会对进气道的气动性能产生较大影响。此外，当进气道的流量捕获系数与总压恢复系数和动能效率不能兼顾时，对于进气道设计还需在总体层面结合燃烧室与喷管的性能进行考虑。对于本文提出的设计方法来说，则完全可以根据总体需求设计波系结构，使进气道的气动性能进一步提升。

仍然需要强调的是，虽然将进气道唇口略微前突至前体激波上游时会带来激波干扰和热防护问题，但从提升流量捕获等总体性能而言，将进气道唇口稍前突还是有利的。

3.3 壁面温度对波系结构的影响

在高超声速条件下，绝热固壁与等温壁面条件对计算结果有较大影响。而且，在工程实践中壁面也并非完全的绝热固壁。为进一步检验本文设计方法在高超声速条件下的应用效果，还需开展等温壁面的数值模拟，检验壁面温度对本文设计方法的影响。

由于IS-2进气道的入射激波与前体激波在设计点存在一定干扰，流场状态更为复杂。因此采用该构型进行设计状态下等温壁面的数值模拟更具代表性。壁面温度Tw选取巡航状态1 000 K和风洞试验状态300 K两种情况。计算网格和其余计算条件设置与绝热固壁条件下的算例一致。计算结果如图11～图12和表4所示。

如图11所示，进气道入射激波、前体激波以及唇罩激波依然相互干扰，而且各激波的相对位置与图7中绝热固壁结果相差很小。这是因为壁面温度主要影响的区域包括进气道和前体的钝化前缘以及进气道的壁面附近。这些影响主要体现在气体热效应强度以及黏性的大小。在马赫数为7.0的来流条件下，气体热效应仅在钝化前缘附近有一定影响，对主流区域的激波形状影响不大。对于黏性来说，经黏性修正后，前体激波以及进气道入口激波的形状在一定程度上兼顾了黏性的影响。这种情况下，这两道激波形状主要由前缘附近的型面和两侧溢流情况决定。虽然壁面温度对附面层厚度有一定的影响，但从激波关系式来看，这些影响并不能使激波形状产生太大的变化。

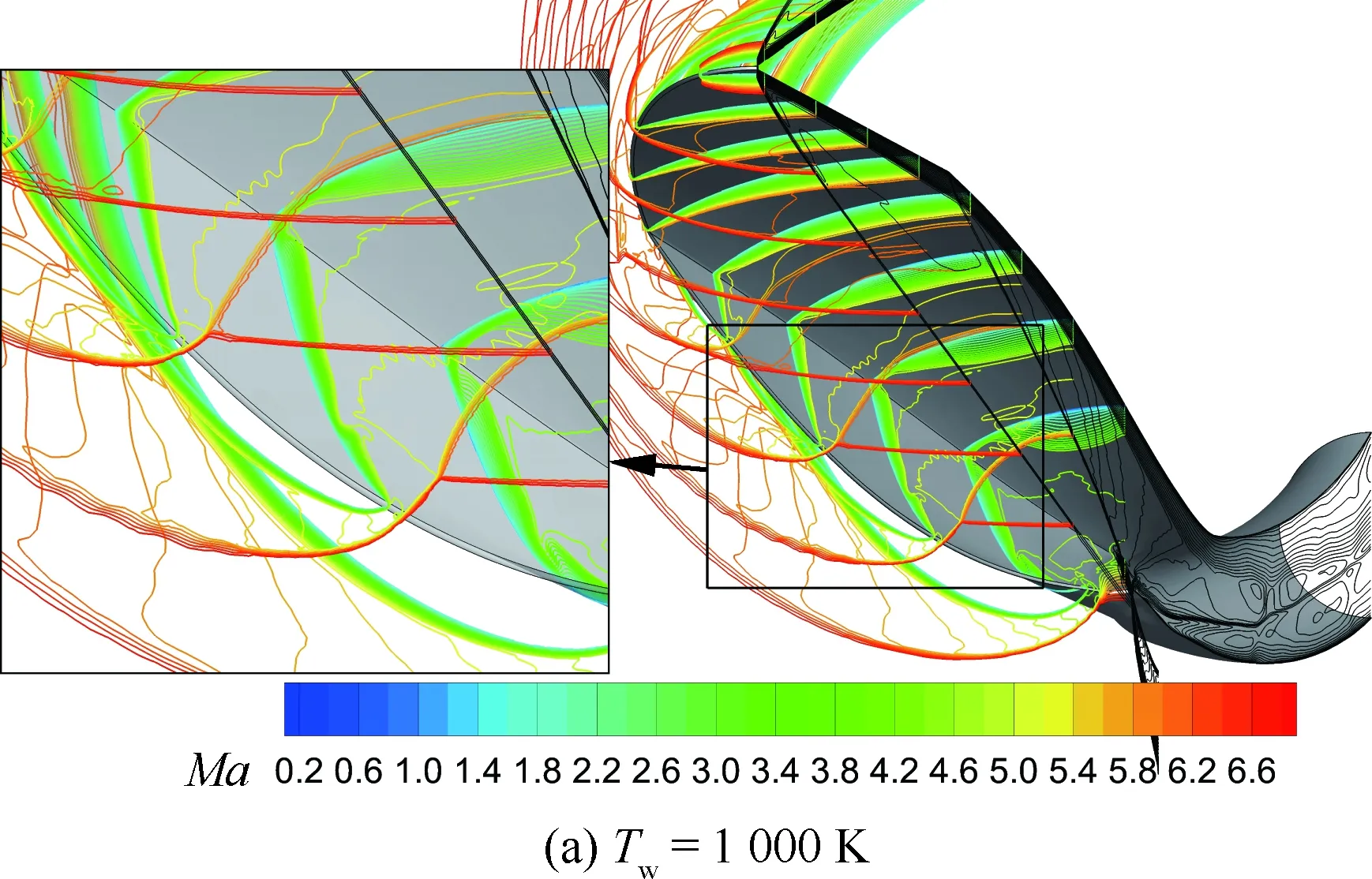
图12给出了进气道对称面的温度(T/T∞)分布。从图12中可以看出，由于壁面散热的影响，附面层内的温度随壁面温度的降低而降低，这必然会导致附面层内马赫数上升。此外，受流场结构影响，对称面处温度边界层与主流之间的分界面形状没有发生较大的变化。这主要是因为在进气道内部壁面温度只能影响通道内的黏性，进而影响到附面层的厚度、激波/附面层相互干扰的强度以及通道涡的大小。但是壁面温度并不能消除这些流动现象。这是因为通道内部的激波是由于气流在通道内部强制偏转产生，通道涡则是通过激波/附面层相互干扰产生，并不受壁面温度直接控制。因此，壁面温度对该进气道通道内部的流场结构不会产生太大影响。

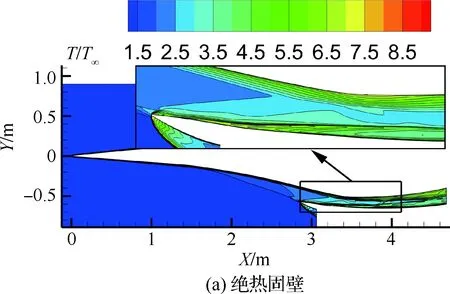
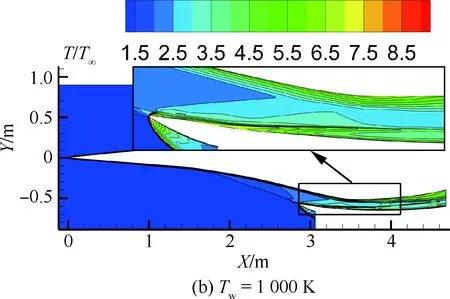
图12 进气道对称面温度分布云图Fig.12 Temperature contours of inlet symmetric plane

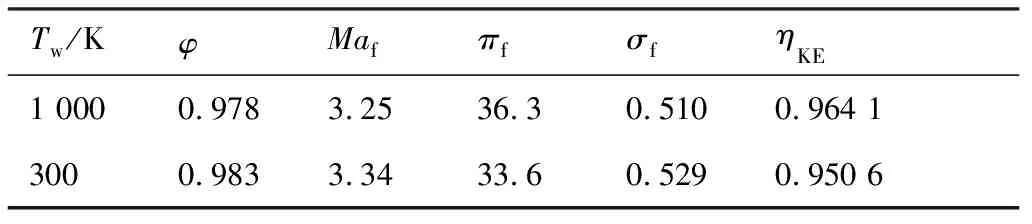
Tw/KφMafπfσfηKE1 0000.9783.2536.30.5100.964 13000.9833.3433.60.5290.950 6

由表4可知，随壁面温度降低，进气道流量捕获系数、隔离段出口截面马赫数、总压恢复系数均有所上升。流量捕获系数的变化原因为：进气道钝化前缘与前方脱体激波的距离随壁面温度降低而降低，在一定程度上抑制了溢流。由于壁面散热使附面层内的黏性影响降低，并间接导致附面层内马赫数上升。这就使得进气道通道内部的激波附面层干扰强度降低，进而使隔离段出口压比下降。总压恢复系数上升主要有两方面原因：① 壁面温度降低使得进气道内部黏性损失降低；② 隔离段出口马赫数上升，导致进气道对气流的压缩程度降低，间接降低了进气道压缩气流的总压损失，最终使总压恢复系数上升。但是由于进气道壁面的散热效果随壁面温度降低而增强，使进气道出口截面气流总焓降低，最终导致动能效率降低。

对于本文的设计方法来说，最重要的部分便是入射激波形状的设计方法。通过等温壁面的研究发现，壁面温度对进气道入射激波形状的影响很小，没有必要在设计方法中专门考虑这种因素。

4 结 论

本文针对典型的乘波前体，开展了基于前体激波的乘波前体/内转式进气道一体化设计方法研究，得到如下结论：

1) 本文发展的内转式进气道设计方法可灵活控制进气道捕获截面的形状，使进气道唇口型线尽可能靠近前体激波，实现进气道与前体激波的匹配。数值模拟结果表明，在马赫数为7.0的来流条件下基于该方法设计的进气道流量捕获系数可以达到0.976，隔离段出口的马赫数、压比和总压恢复系数分别达到3.17、38.9和0.487，在马赫数4.5～7.0的范围内均可有效工作。

2) 通过本文研究发现，当乘波前体下方流场的均匀性较好，且速度方向偏转角度较小时，仍然可以应用本文方法设计性能较好的内转式进气道。

3) 发展了基于进气道入射激波形状和波后沿程马赫数分布的基本流场设计方法。应用该方法不但可以通过调节入射激波形状使进气道唇口型线和前体激波实现较好匹配，还可以通过沿程马赫数分布有效提升进气道的气动性能，进一步提升了内转式进气道在一体化设计过程中的灵活性。

4) 数值模拟结果表明，当进气道唇口略微前突至前体激波上游时，流量捕获系数提升1.45%，而总压恢复系数和动能效率则分别下降2.6%和1.02‰。这说明，进气道唇口略微前突至前体激波上游时，进气道的气动性能还有一定的提升。

5) 通过等温壁面的数值模拟发现，在马赫数7.0的来流条件下，壁面温度对喉道上游流场影响较小，在基本流场的设计中可不做专门处理。但是，壁面温度对隔离段内的影响较为明显，为此还需要结合整个流场的流动机理进行深入研究。