航空电连接器接触件疲劳寿命的可靠性分析

杨强，闻聪聪，孙志礼，张孟君

1. 东北大学 机械工程与自动化学院，沈阳 110819 2. 东北大学 航空动力装备振动及控制教育部重点实验室，沈阳 110819 3. 沈阳兴华航空电器有限责任公司，沈阳 110144

军用航空电连接器是武器装备中广泛应用的基础性元器件，电连接器接触件是实现电路导通和信号平稳传递的重要部件[1]。开展航空电连接器可靠性建模研究对于评估接触件的可靠性和预防因接触件失效而导致重大安全事故具有重要的实际工程意义。

目前，对电连接器的可靠性研究多集中于对电连接器的接触可靠性的探索。Li等[2]研究了不同结构参数对接触件插入力的影响并分析了电连接器的接触可靠性。Malucci[3]通过试验手段建立了接触力和微动振幅对电连接器接触性能退化影响的预测模型。Flowers等[4-5]利用ANSYS有限元分析软件模拟了电连接器在微动腐蚀条件下的接触性能，并进行了实验验证。Seehase[6]在加速寿命实验的基础上建立了一种可以预测接触电阻变化的理论模型，并分析了评估电连接器接触可靠性的2个主要影响因素。陈文华和李平真[7]对航天电连接器进行了失效机理分析，建立了评价其接触寿命特征的可靠性数学模型。Beloufa[8]用有限元仿真和实验相结合的方法，研究了汽车用铜合金电连接器接触件不同的几何尺寸和接触力对接触电阻的影响。文献[9]通过分析电连接器在振动应力作用下的失效机理，建立了失效物理模型并进行了实验验证。黄超群等[10]对尘土存在条件下电连接器的接触可靠性进行了研究。潘骏等[11]对电连接器进行了结构力学分析和接触情况研究，并通过实验验证了理论分析和仿真分析的可行性。王世娇等[12]在综合考虑电连接器接触件尺寸、工艺和材料参数与其可靠性指标之间关联性的前提下，建立了电连接器可靠性设计的数学模型，并提出了电连接器可靠性定量设计的方法。

接触件疲劳失效是导致电连接器失效的重要原因之一[13-14]。Huang等[15]提出了一种电连接器的三维有限元模型用以研究其微动磨损的力学性能和接触性能，并给出了评估其疲劳寿命的计算方法。文献[16]以微型电连接器为研究对象，依据疲劳寿命预测理论和S-N曲线对电连接器的危险部位进行了疲劳寿命预测。Li等[17]设计了一种加速寿命实验方法，并据此建立了电连接器接触件疲劳寿命的可靠性预测模型。

接触件制造和配合误差的存在是降低接触疲劳寿命从而造成接触件疲劳失效的主要影响因素之一。本文针对某型航空电连接器，利用三维建模软件实现了接触件的参数化建模，联合使用有限元分析软件对接触件进行了单次插拔过程的接触性能分析。然后，利用疲劳分析软件建立了疲劳寿命的仿真计算模型。同时，考虑制造误差和配合误差的随机性，利用蒙特卡罗法得到电连接器的疲劳寿命分布类型，进而完成了航空电连接器接触件疲劳寿命的可靠性建模，实现了对接触件疲劳寿命的概率预测，为预防电连接器发生疲劳失效和满足可靠寿命要求下接触件制造和装配过程中关键工艺参数(公差带等)的合理选用提供理论基础。

1 单次插拔过程接触性能分析

1.1 三维CAD模型的建立

以某型军用航空电连接器38999系列通用接触件22#插针插孔为研究对象，利用SOLIDWORKS三维建模软件，建立插针插孔参数化模型如图1(a)所示，其中，插针的直径为0.762 mm，插孔端部开口尺寸为0.65 mm插孔端部缩孔精确建模局部放大如图1(b)所示。

1.2 单次插拔过程力学特性分析

图1 插针插孔参数化模型Fig.1 Drawings of parametric model for pin and jack

将插针插孔SOLIDWORKS三维配合模型导入ABAQUS中进行有限元分析。接触件22#插针与插孔的材料特性如表1所示。网格划分时，选择C3D10M四面体单元。由于插孔端部进行了缩孔，当插针插入插孔时接触件之间的接触类型为面面接触。无润滑条件下，接触件之间的摩擦系数设为0.13。最后，利用ABAQUS软件仿真分析接触件在单次插拔过程中的接触性能。

由图2可以看出，插针头部刚刚插入插孔端部时，插针和插孔接触的位置以及插孔簧片的根部等效应力和等效应变较大。

在插针不断插入插孔过程中，簧片的变形量亦随之不断增大。当插针头部完全插入插孔时，如图3所示，最大等效应力和最大等效应变的位置均在插孔簧片的根部。

从图3可以看出，插针完全插入插孔时，插孔簧片的根部区域的应力最大且超过了材料的屈服极限，但是所占比例很小。由文献[11]分析可知，簧片根部开槽处发生了应力集中，设计过程中应该尽量避免这种情况的出现。

图4表示簧片根部的应力分布情况，应力最大值为299 MPa，超过了材料的屈服极限280 MPa。因此在接触件工作过程中，插孔簧片的根部率先发生塑性变形。当塑性变形累积到一定量时，插孔簧片根部某些部位会萌生裂纹。此时，随着插拔次数的增加，裂纹不断扩展，当达到一定长度时插孔簧片易发生整体断裂，严重影响航空系统的可靠性。

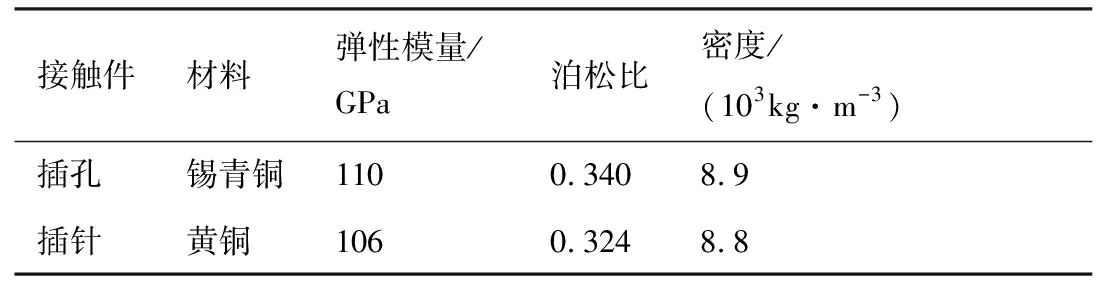
表1 接触件的材料特性Table 1 Material properties of contact parts

为了直观地观察接触件单次插拔过程中簧片根部等效应力和应变最大值处单元节点的应力和应变的变化情况，在ABAQUS软件输出结果中输出该危险节点在仿真过程中的等效应力和应变曲线，如图5所示，图5中0～2 s表示插针插入插孔过程，2～3 s表示插针拔出插孔过程。接触件插拔力的变化如图6所示。

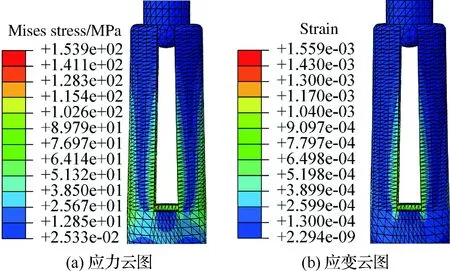
图2 插针头部刚插入插孔时的应力和应变云图Fig.2 Stress and strain nephograms when the head pin is just plugged into the jack

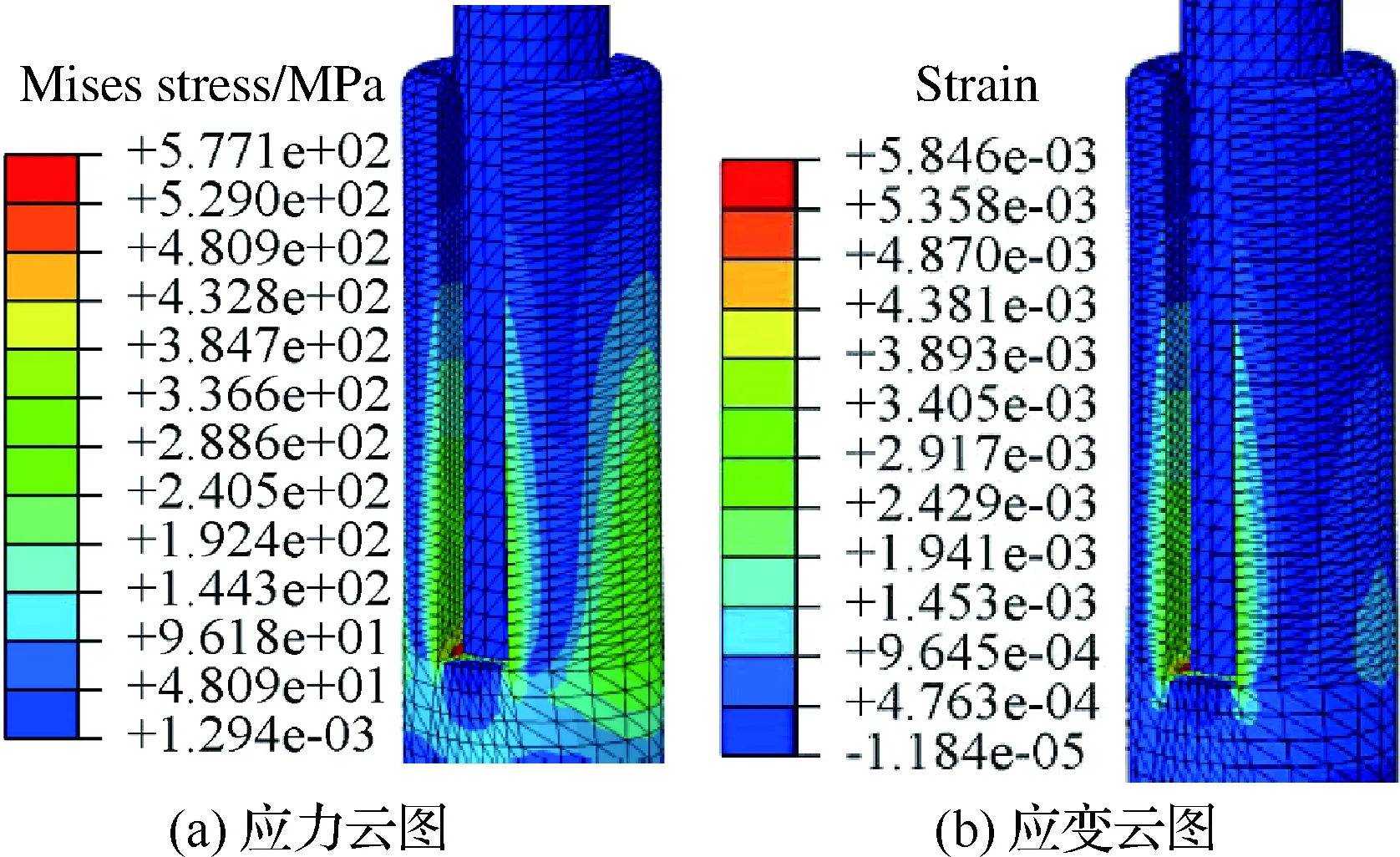
图3 插针完全插入插孔时的应力和应变云图Fig.3 Stress and strain nephograms when the pin is plugged completely into the jack

图4 簧片根部应力分布Fig.4 Stress distribution at root of reed

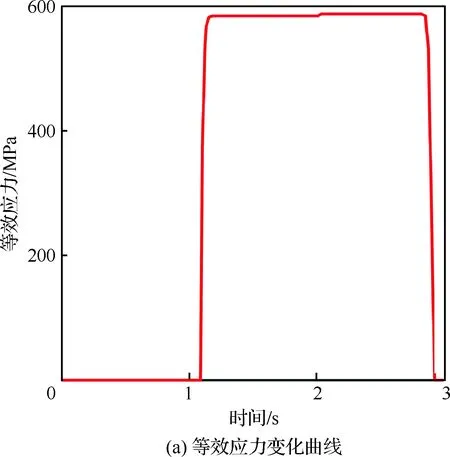
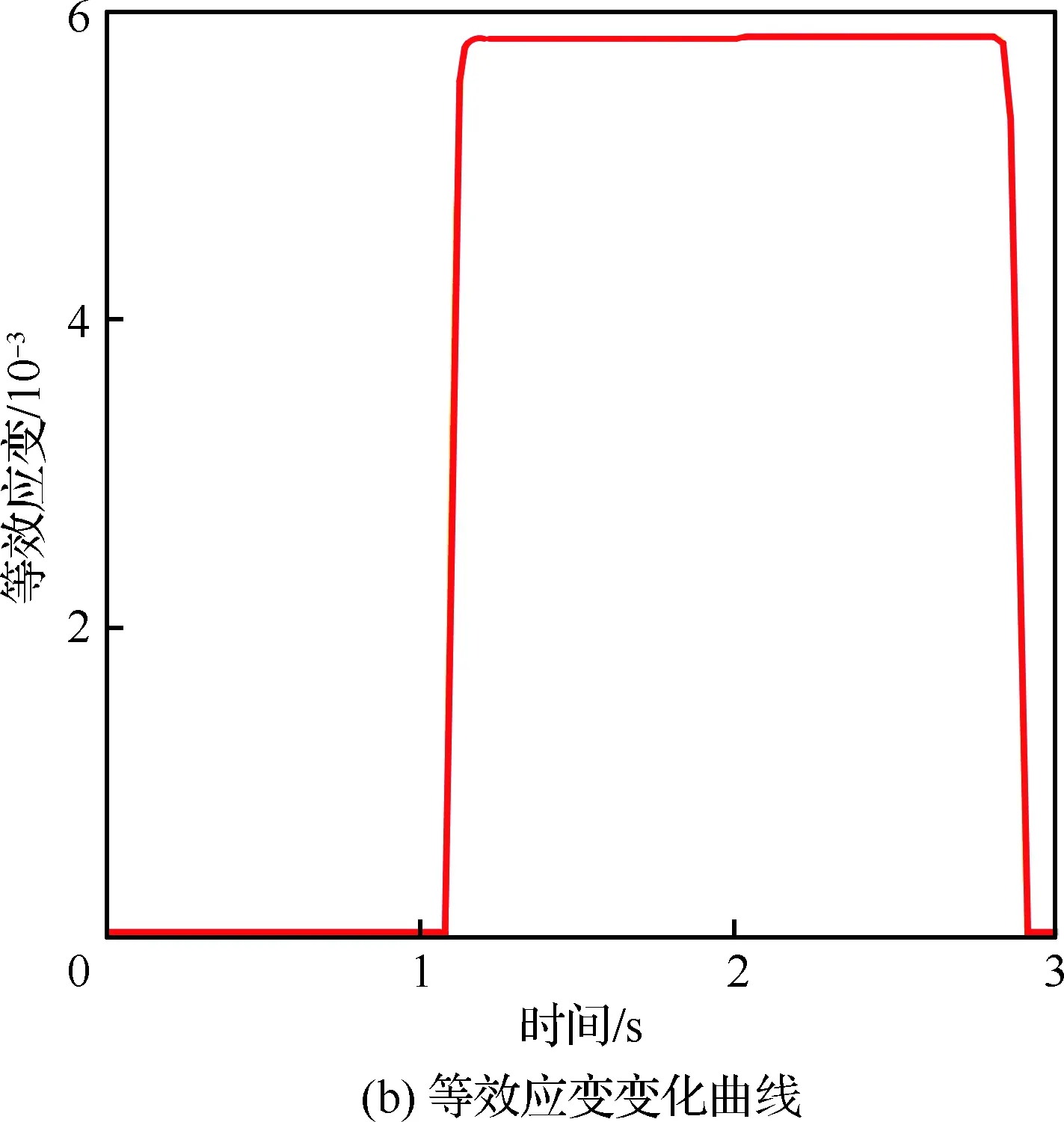
图5 等效应力和应变最大位置处变化曲线Fig.5 Variation curves of maximal equivalent stress and strain

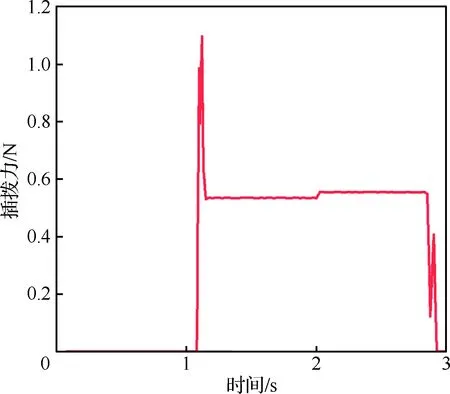
图6 插孔与插针之间的插拔力Fig.6 Plugging-pulling force between jack and pin

2 接触疲劳寿命分析

2.1 疲劳失效物理模型

双簧片接触件的截面形状如图7(a)所示，面积为：A=A1-A2，A1和A2分别为图7(b)和图7(c)的面积，且A1和A2的值为

(1)

式中：R和r分别为图7(b)和图7(c)中对应的圆弧半径；α1和α2分别为其对应圆心角的大小。

通过查阅机械设计手册[18]可得图7(b)和图7(c)中弦的高度分别为h1=R[1-cos(α1/2)]和h2=r[1-cos(α2/2)]。它们的重心到x1轴的距离y1和y2分别为

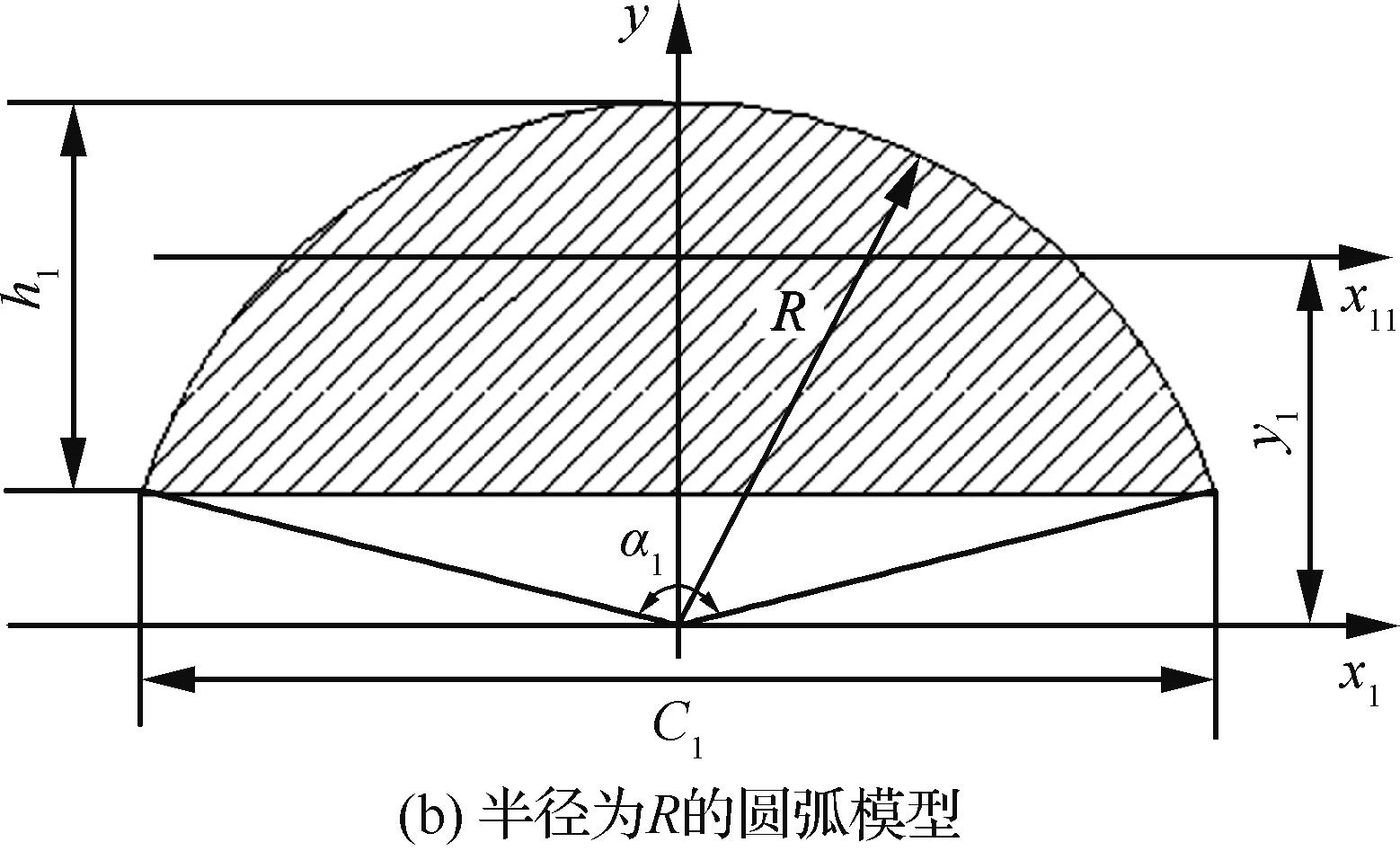
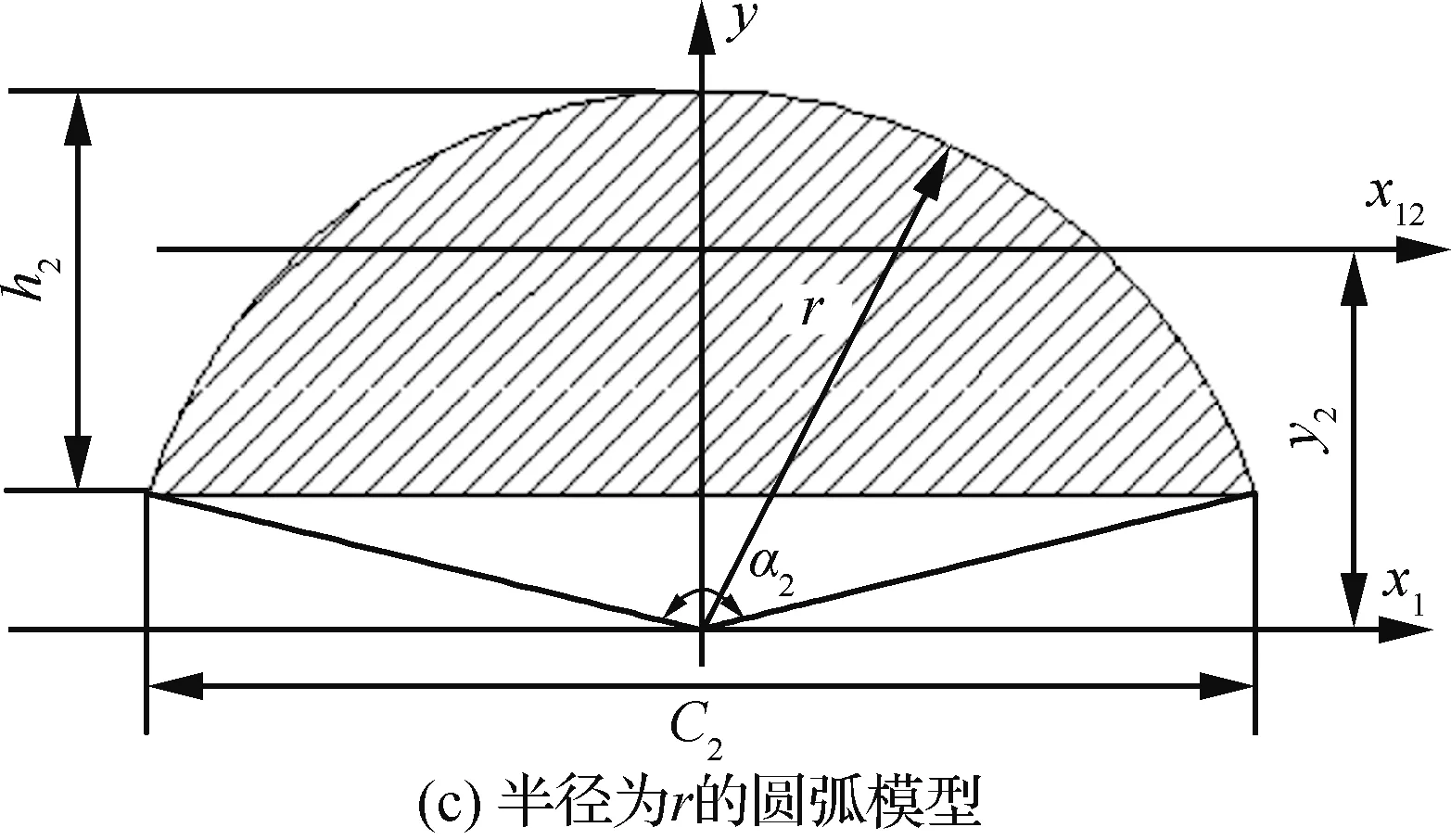
图7 双开槽接触件插孔簧片的截面图Fig.7 Sectional picture of jack reed of double groove contact

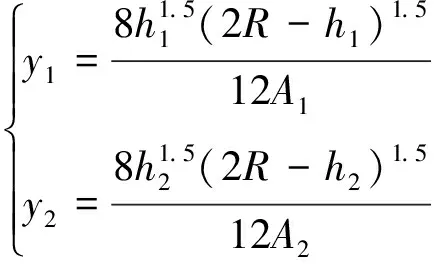
(2)

图7(a)的重心到x1轴的距离为

(3)

式中：R、r和h均已知，且由图7可知h1=h、h2=h-(R-r)，从而可计算出y的值。图7(b)和图7(c)对x1的惯性矩分别为

(4)

由此可知图7(a)对x轴的惯性矩为

Ix=Ix1-Ay2

(5)

式中：Ix1=Ix11-Ix12。为了便于研究接触件间的接触压力，将插孔结构简化为悬臂梁模型，如图8所示。

由此可推出接触压力和接触压力对插孔簧片根部的弯矩分别为

(6)

M=FL

(7)

式中：δ为簧片的挠度；L为簧片长度；E为簧片材料的弹性模量。经分析可知，最大等效拉应力的位置出现在图7(a)半圆环的下端点处，且下端点到中性层轴的距离为s=h- (R-y)，因此，插孔簧片根部最大等效拉应力为

(8)

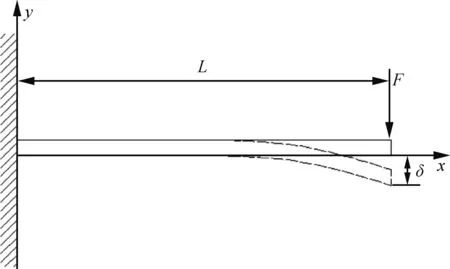
图8 插孔簧片等效模型Fig.8 Equivalent model for jack reed

工程实际中，I型裂纹(如图9(a)所示)最为常见且危害度最高[19]。从簧片的结构和受力特点可知簧片根部开槽处裂纹为I型。因此，应用无限宽长条板有单边裂纹且受无穷远处均匀拉伸模型(如图9(b)所示)，得到材料的应力强度因子[20]为

(9)

式中：a为裂纹长度。

同时，通过以上的有限元分析可知最大等效应力出现在簧片根部开槽处，且该值大于锡青铜的屈服极限，导致开槽处在小范围内会发生塑性变形，此时应力强度因子已不足以作为断裂依据。因此，利用工程上较为常用的Irwin小范围屈服条件下的裂纹尖端张开位移(CTOD)准则[19]对该范围屈服的塑性区进行修正，得到裂纹尖端张开位移为

(10)

式中：σs为材料的屈服极限；v为裂纹沿y方向的位移，且其值为

(11)

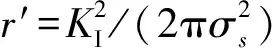
Δ≥Δc

(12)

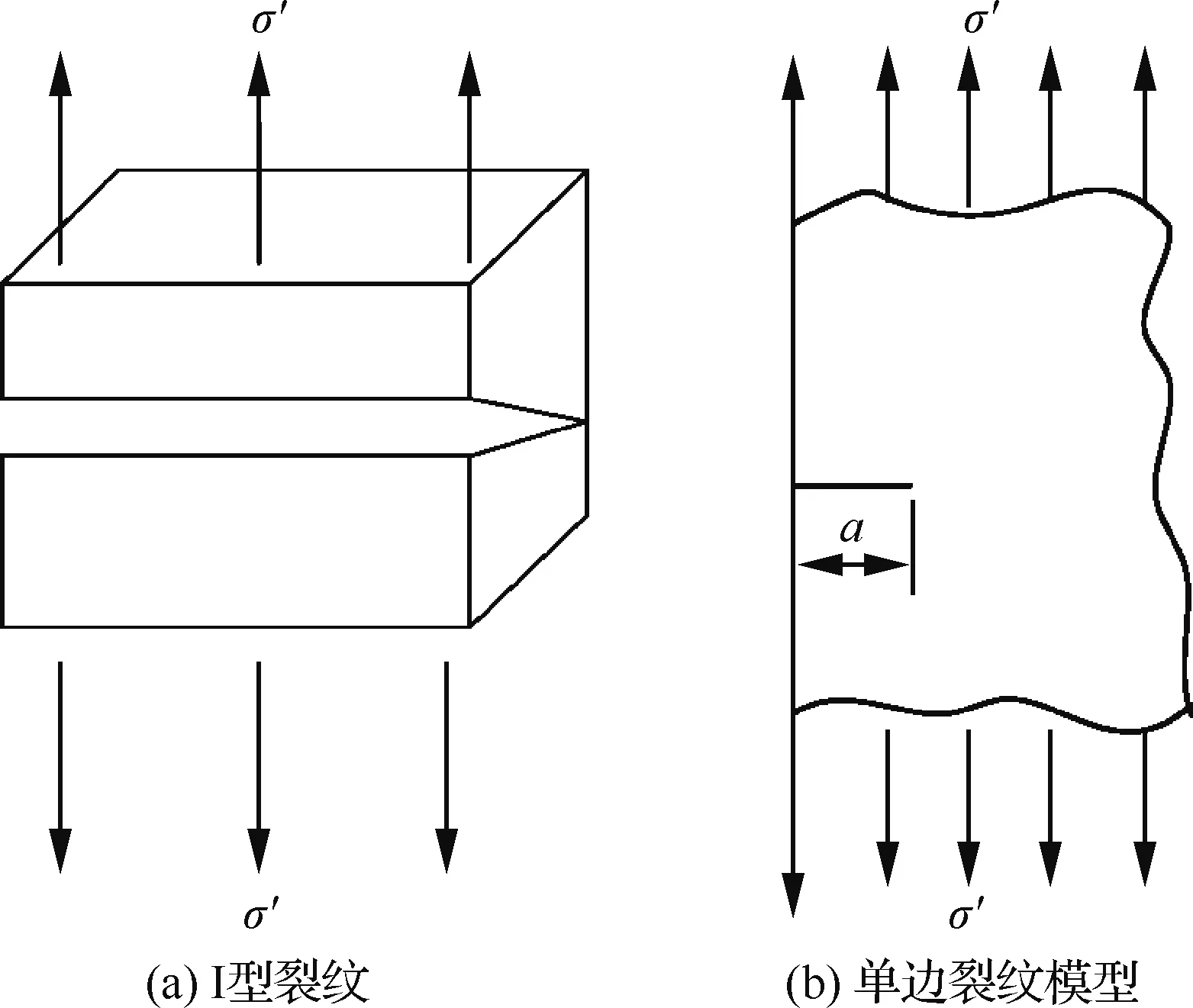
图9 I型裂纹及单边裂纹模型Fig.9 Crack of mode I and model for single-edge crack

2.2 应变-寿命方程式的建立

在使用FE-SAFE软件进行疲劳分析前，需首先建立接触件的寿命评估模型。考虑到某型电连接器接触件材料锡青铜为韧性较好的金属材料，因此选择适应于求解韧性材料疲劳寿命的Brown-Miller临界平面法建立其疲劳寿命评估模型。将传统的应变-寿命方程式左边以剪切应变幅值和法向应变幅值表示，则可得到Brown-Miller应变寿命方程为

(13)

式中：Δγmax为最大剪应变范围；Δεn为最大剪应变平面上的法向应变范围；σf为疲劳强度系数；εf为疲劳延性系数；b为疲劳强度指数；c为疲劳延性指数；Nf为以循环数计的疲劳寿命；C1为弹性情况下的实常数；C2为塑性情况下的实常数。

对于弹性问题，材料的泊松比υ=0.34，Δγmax=(1+υ)Δε1=1.34Δε1，Δεn=(1-υ)Δε1/2=0.33Δε1,则C1=1.34+0.33=1.67，Δε1为主应变。对于塑性问题，泊松比υ=0.5，同理，计算得C2=1.75。

将以上参数值代入式(13)可得Brown-Miller应变-寿命方程为

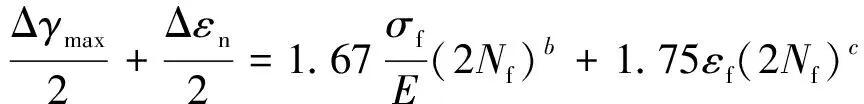
(14)

由于制造和装配误差的存在，插孔在插拔过程中承受的应力是不均匀的，因此需要用Morrow平均应力法进行修正。设平均正应力为σm,n，则修正后的Brown-Miller应变-寿命方程为

(15)

本文研究的接触件材料为锡青铜，其屈服极限σs=280 MPa，弹性模量E=110 GPa，在FE-SAFE软件中采用Seeger估算法得到其疲劳性能数据如表2所示，即式(15)中b=-0.087，c=-0.58，σf=420 MPa，εf=0.59。根据以上数据，在FE-SAFE软件中拟合接触件材料的应变-寿命曲线，如图10所示。

表2 锡青铜的疲劳性能Table 2 Fatigue properties of tin bronze

图10 应变-寿命曲线Fig.10 Curve of strain-life

2.3 接触疲劳寿命仿真求解

零件的疲劳寿命理论求解一般采用系数修正法进行近似计算，而疲劳寿命的仿真求解则基于软件内嵌的疲劳分析算法较为充分地考虑了零件的结构细节和载荷历程。因此，本文采用联合ABAQUS和FE-SAFE软件对接触件的疲劳寿命进行仿真计算，仿真流程如图11所示。

由有限元分析可知接触件在受载过程中，单元节点上主应力的大小和方向不断发生变化，即接触件易发生多轴疲劳失效，因此选择临界平面法对接触件进行疲劳寿命的分析计算。临界平面法通常分为2步，首先计算出疲劳临界面上的应力-应变历程，然后将临界面上的应力-应变转化为疲劳累积损伤，即使用修正后的Miner法则[21]计算出节点的最终疲劳寿命。电连接器在插拔过程中应力集中主要出现在插孔上，因此，为减少计算量，仅对插孔进行疲劳寿命求解。将ABAQUS有限元分析的结果文件导入到FE-SAFE中，以单次插拔过程中接触性能为边界条件对接触件进行疲劳寿命计算。其FE-SAFE关键分析步骤如下所述。

1) 接触件材料的定义

采用Seeger算法近似估算接触件锡青铜材料的疲劳性能。将σs=280 MPa、E=110 GPa输入到图12所示的对话框中，FE-SAFE会自动得到锡青铜材料的疲劳性能参数。

2) 接触件疲劳算法选择

由2.2节内容分析可知，接触件疲劳算法选择Brown Miller-Morrow算法，如图13所示。

3) 接触件疲劳寿命计算与分析

基于接触件插孔材料裂纹萌生准则， FE-SAFE仿真计算结果为：接触件疲劳寿命仿真值为2 205.502次。将FE-SAFE计算结果文件导入ABAQUS中，在ABAQUS中显示接触件的疲劳寿命云图，如图14所示。由图14可知，多次插拔作用后，插孔簧片根部位置出现了明显的疲劳损伤。

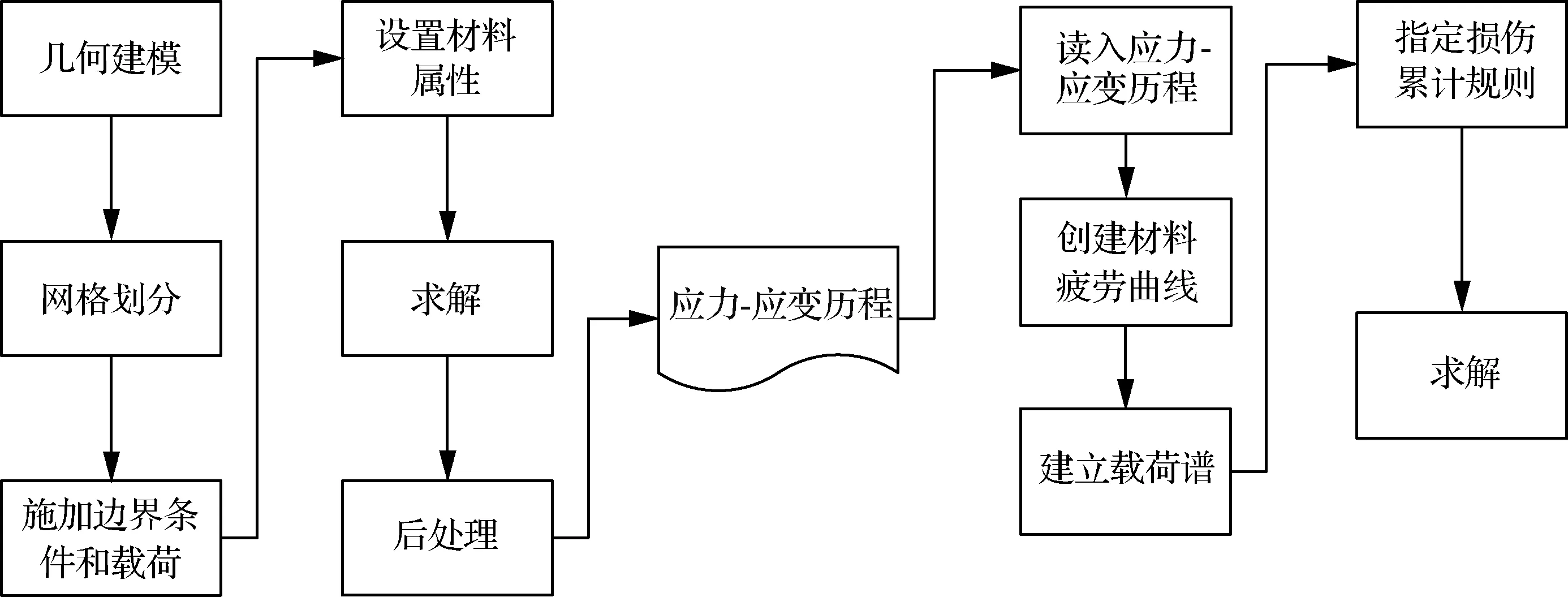
图11 疲劳寿命仿真分析流程Fig.11 Flowchart of fatigue life simulation analysis

对比图14和图3(a)可知，ABAQUS的应力应变分析结果云图和FE-SAFE的疲劳损伤结果云图完全吻合。

图12 锡青铜材料疲劳参数估算Fig.12 Estimation of fatigue parameters of tin bronze

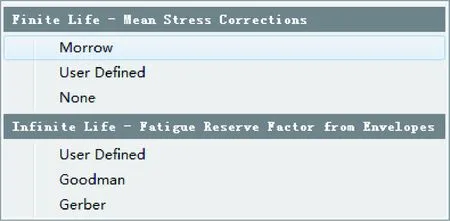
图13 疲劳算法和修正准则定义Fig.13 Fatigue algorithms and definition of correction criteria

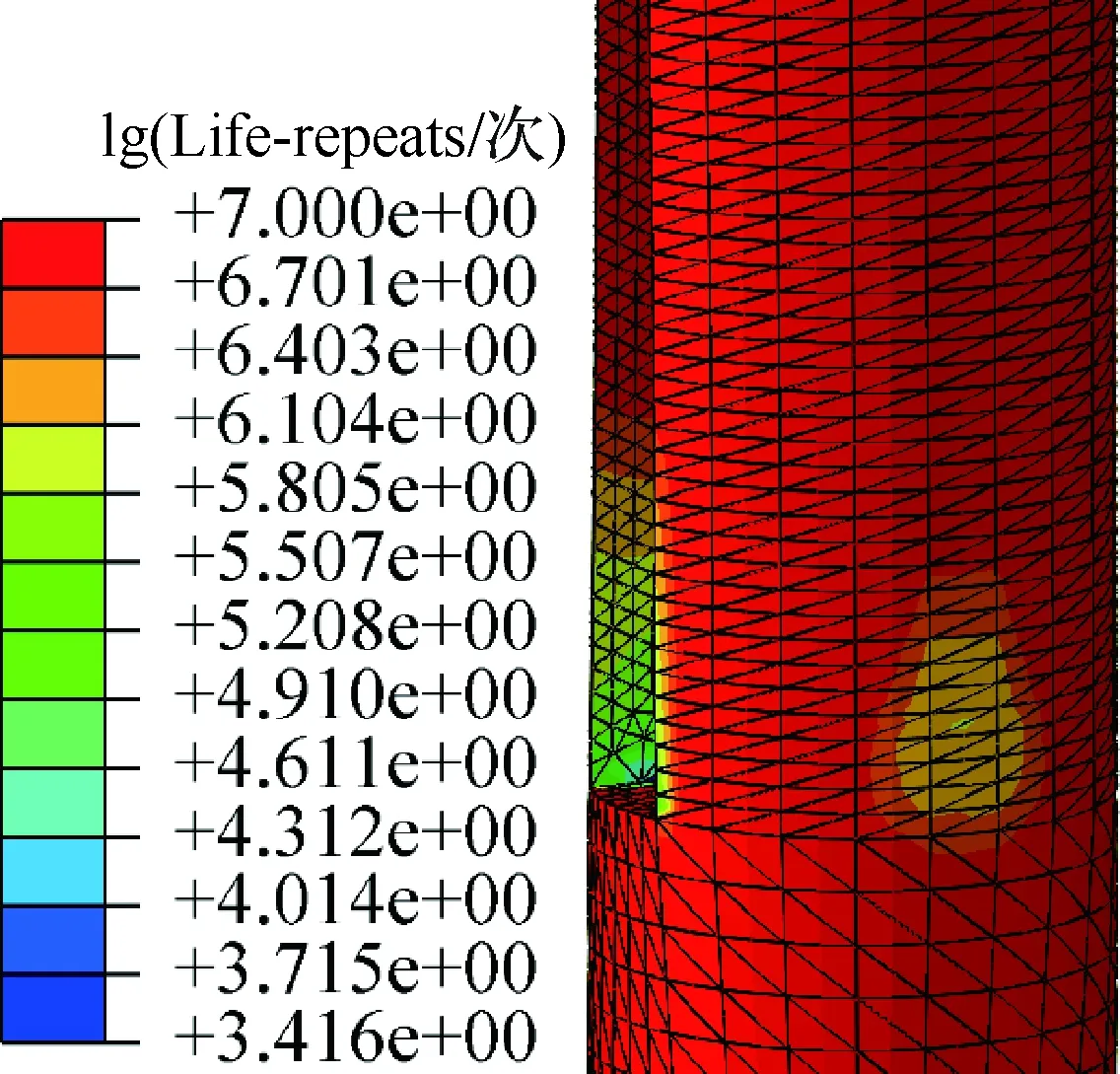
图14 插孔疲劳寿命的对数云图Fig.14 Nephogram of logarithm of fatigue life of jack

3 误差影响下接触疲劳寿命的可靠性分析

电连接器接触件的接触疲劳寿命是指接触件经过若干次插拔工作循环后，插孔簧片根部位置萌生裂纹，若继续工作，则插孔簧片与插针的接触压力无法保证信号的稳定传递。

3.1 制造误差的影响

以插孔为研究对象，研究插孔簧片长度、端部开口尺寸以及开槽宽度等3种制造误差对电连接器接触疲劳寿命的影响。将ABAQUS软件分析得到的结果文件导入FE-SFAE中，并以接触件单次插拔的应变作为边界条件，分别对3种制造误差对电连接器疲劳寿命的影响进行定量分析[22]。

1) 插孔簧片长度误差的影响

理想条件下，单独分析插孔簧片长度误差对电连接器疲劳寿命的影响。基于某型军用航空电连接器接触件的设计图纸公差带，将插孔簧片的分析长度分别取为2.97、2.98、2.99、3.00、3.01、3.02和3.03 mm。将在各个长度值下分析得到的接触件疲劳寿命在同一坐标系中用光滑曲线连接，如图15所示。

从图15可以看出，当插孔簧片长度小于设计尺寸3.00 mm时，接触件的疲劳寿命总体呈下降趋势，这是因为插孔簧片长度减小，插针插入插孔过程中簧片的挠度相对加大，导致簧片根部所受应力变大，从而严重减少了接触件的疲劳寿命；当插孔簧片长度大于设计尺寸时，虽然接触件的疲劳寿命上下波动幅度较大，但是总体亦是呈下降趋势，这是由于簧片长度加大时，接触件的接触性能变差，导致疲劳寿命的降低，且此时簧片长度已不满足国军标的要求。

2) 插孔开槽宽度误差的影响

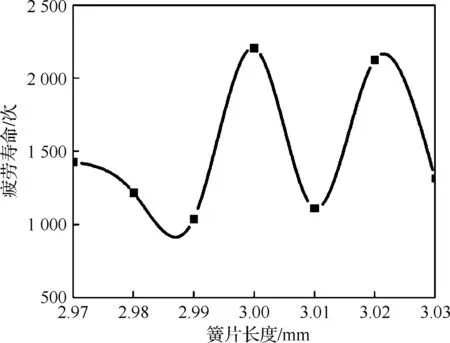
图15 插孔簧片长度对电连接器疲劳寿命的影响Fig.15 Influence of length of jack reed on fatigue life of electric connector

同理，插孔开槽宽度对接触件疲劳寿命的影响如图16所示。当插孔的开槽宽度小于设计尺寸0.40 mm时，插针插入插孔过程中，插孔的挠度相对增大，使得插孔簧片根部的应力增大，接触件的疲劳寿命随之降低；当插孔的开槽宽度大于设计尺寸时，在一定范围内，接触件的疲劳寿命呈上升趋势，但过大的开槽宽度亦会使接触件之间的分离力过小，导致不满足国军标对接触件分离力的要求。

3) 插孔端部开口尺寸制造误差的影响

图17表示插孔端部开口尺寸对电连接器疲劳寿命的影响，从图17中可以看出，当插孔端部开口尺寸小于设计尺寸0.65 mm时，随着插针插入插孔，插孔簧片变形量不断增加，簧片根部应力亦随之增大，导致接触件的疲劳寿命降低；当插孔端部开口尺寸大于设计尺寸时，接触件的疲劳寿命总体呈上升趋势，但是，此时接触件之间的分离力会迅速降低，不满足国军标的要求。

图16 插孔开槽宽度对电连接器疲劳寿命的影响Fig.16 Influence of slot width of jack on fatigue life of electric connector

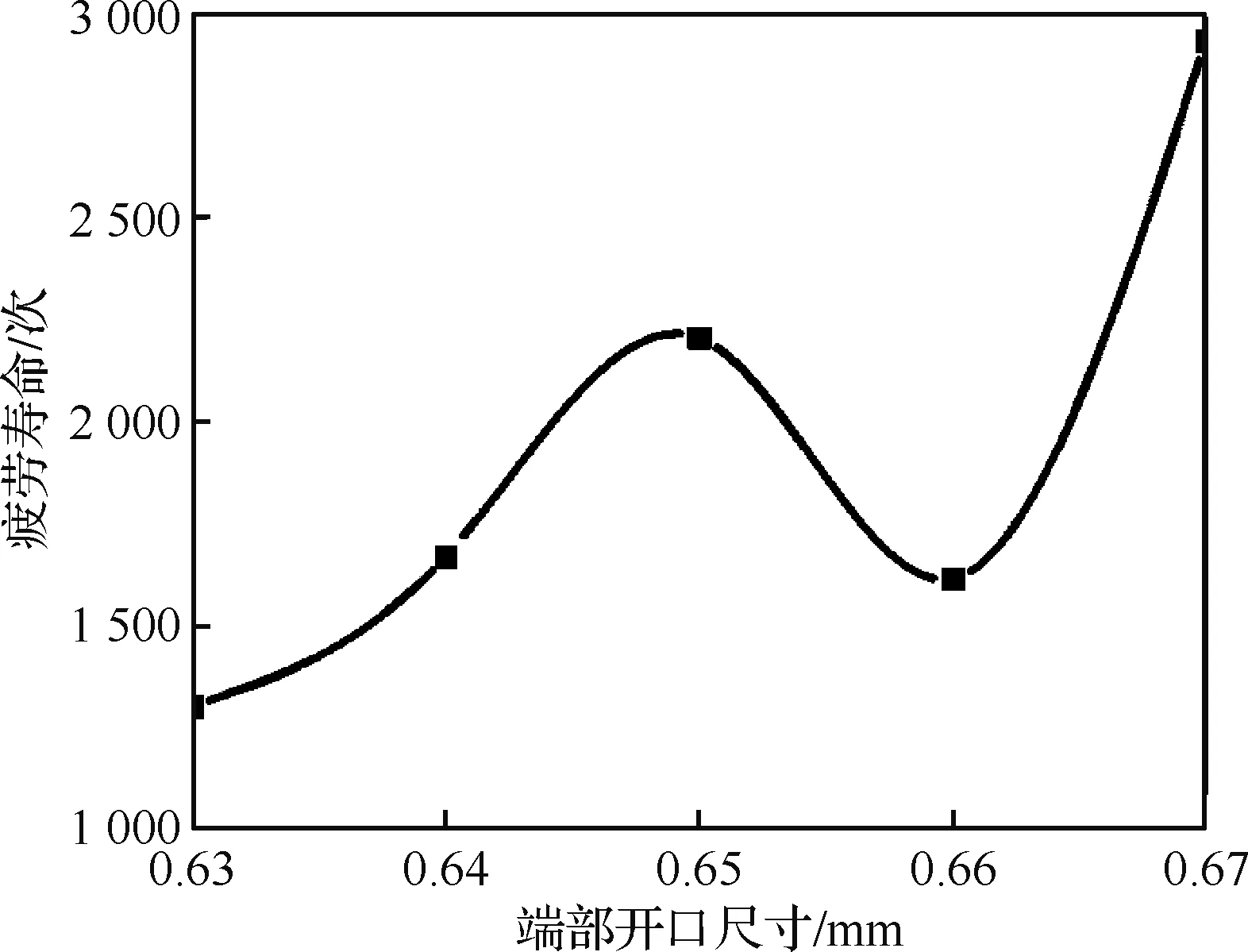
图17 插孔端部开口尺寸对电连接器疲劳寿命的影响Fig.17 Influence of opening size at end of jack on fatigue life of electric connector

3.2 配合误差的影响

电连接器在装配过程中可能存在配合误差，使得插针中心偏离插孔中心，导致插针和插孔内壁出现过度挤压现象甚至容易造成接触件断裂，严重影响了接触件的疲劳寿命和整个系统的安全性。本文就位移误差和角度误差，联合利用ABAQUS软件和FE-SAFE软件定量分析了2种配合误差对接触件疲劳寿命的影响。

1) 位移误差的影响

位移误差是指接触件配合时，两者的轴线不重合而存在一定的径向偏移量。从图18中可以看出，疲劳寿命随着位移误差的不断增大而降低。由于位移误差的存在，导致插针在插入插孔过程中过度挤压插孔一侧簧片，同时插孔簧片还需克服因插针直径与插孔端口尺寸不同而引起的变形，从而加剧了插孔簧片在接触过程中的变形；随着位移误差的不断增大，接触件间的正压力以及插孔簧片根部最大等效应力亦不断增加，进而导致接触件的疲劳寿命随着位移误差的递增而逐渐降低。

同时，从图18中可以看出电连接器的疲劳寿命随着一定范围内的位移误差呈现出很强的规律性，通过MATLAB拟合计算可得到在满足500次插拔要求下，该型电连接器接触件允许的最大位置误差为0.054 mm。

2) 角度误差的影响

图18 接触件疲劳寿命随着位移误差增大的变化曲线Fig.18 Variation curve of fatigue life of contact partswith increase of displacement error

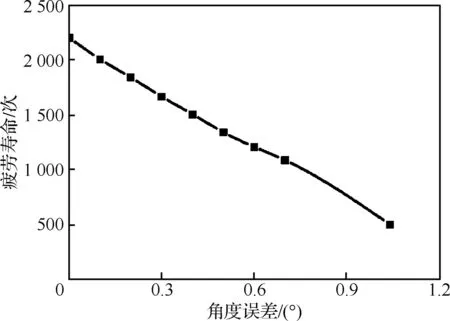
图19 接触件疲劳寿命随角度误差增加的变化曲线Fig.19 Variation curve of fatigue life of contact parts with increase of angle error

角度误差是指接触件配合时，两者的轴线不重合而是存在一定的偏角。接触件疲劳寿命随角度误差的变化如图19所示。电连接器的疲劳寿命随着角度误差的加大而呈近似线性减小趋势。这是因为装配时的角度误差使得插针与插孔接触过程中，插针的实际直径增大，进而导致接触件在插入和拔出时插孔簧片的变形量增加，接触件间的正压力和插孔簧片根部的最大等效应力亦增大。

同时，从图19可以看出电连接器的疲劳寿命随着一定范围内的角度误差呈现出线性变化规律。利用MATLAB拟合计算可得到在满足500次插拔 要求下，该型电连接器接触件允许最大的角度误差为1.041°。

3.3 接触疲劳寿命的可靠性分析模型

假定制造误差和配合误差均服从正态分布，基于图纸公差带要求和“3σ方法”令开槽宽度X1～N(0.4,0.016 72) mm，簧片长度X2～N(3.00,0.016 72) mm，端部开口尺寸X3～N(0.65,0.012) mm， 配合角度Y1～N(0,0.139 2) (°)，配合位移Y2～N(0,0.023 2) mm。基于蒙特卡罗仿真抽样技术，利用MATLAB软件，对该型军用航空电连接器接触件插孔的开槽宽度、簧片长度、端部开口尺寸以及插针和插孔在装配过程中出现的角度误差以及位移误差进行10 000次抽样，然后利用得到的抽样数据对接触件进行三维建模并进行有限元分析，进而对其疲劳寿命进行求解。表3为计算得到的接触件疲劳寿命数据。

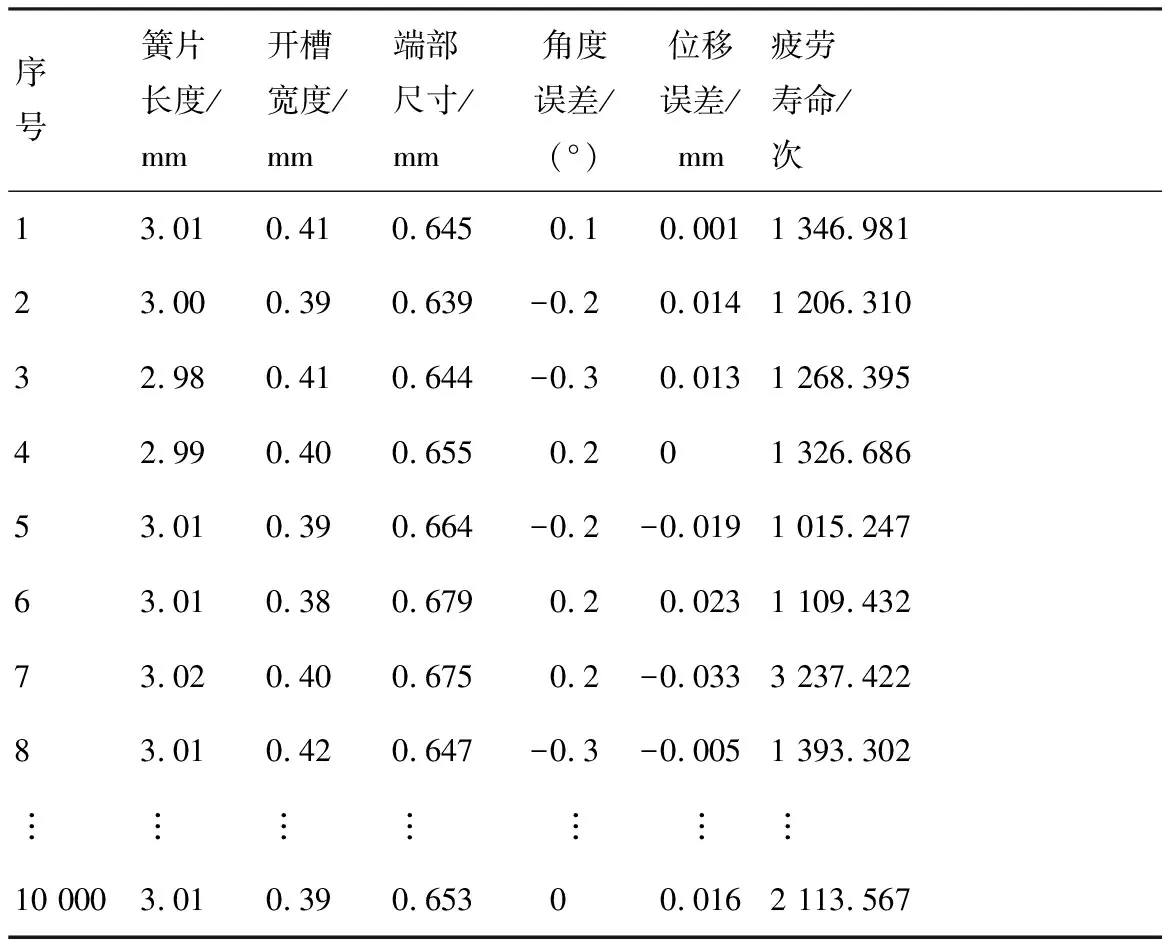
表3 电连接器接触件抽样尺寸的疲劳寿命

根据表3接触件的疲劳寿命计算结果，利用MINITAB软件进行统计分析，选择置信区间为95%，对比各类分布的拟合优度检验的AD值和P值，最终确定接触件的疲劳寿命服从三参数的威布尔分布，并且：尺度参数为η=2 583.963；形状参数为β=2.454；位置参数为x0=69.231 2。其疲劳寿命的概率密度函数和分布函数分别为

x≥x0

(16)

(17)

根据三参数的威布尔分布失效概率密度函数和可靠度函数，画出疲劳寿命的概率密度曲线和可靠度曲线如图20所示。

设电连接器接触件的设计疲劳寿命为[L]，计算疲劳寿命为L(i)，为保证电连接器正常工作要求接触件的计算寿命大于等于其设计寿命，则该接触件疲劳寿命可靠度的计算式为

(18)

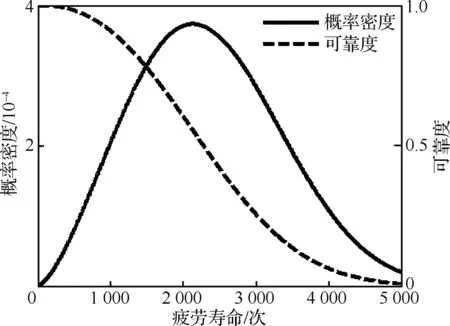
图20 电连接器接触件疲劳寿命的概率密度和可靠度曲线Fig.20 Probability density and reliability curves of fatigue life of contact parts of electrical connector

根据GJB 599A—1993，该型电连接器接触件插拔寿命不小于500次，即令设计寿命[L]=500，则其可靠度为

(19)

(20)

4 结 论

1) 考虑插孔制造误差和插针插孔配合误差的随机性，基于接触件疲劳寿命的仿真模型，提出了军用航空电连接器接触件疲劳寿命的可靠性建模技术。对应接触件疲劳寿命为常数的情况，给出了电连接器接触件疲劳寿命的可靠度计算方法。实现了工程实际中，电连接器在经历任意次插拔后疲劳寿命的可靠度预测。

2) 基于所建立的可靠性模型，计算得出某型航空电连接器的接触件疲劳寿命服从尺度参数为η=2 583.963；形状参数为β=2.454；位置参数为x0=69.231 2的三参数威布尔分布。依据GJB 599A—1993标准，某型军用航空电连接器的许用寿命为500次，其接触件的疲劳寿命可靠度为98.78%。

3) 电连接器接触件疲劳寿命随着插孔簧片长度、端部开口尺寸、开槽宽度3种制造误差的增大出现无规律波动现象；随着位移和角度2种配合误差的增大呈现有规律的减小趋势。根据GJB 599A—1993要求，在满足500次插拔要求下，该型电连接器接触件允许最大的位置误差为0.054 mm，最大的角度误差为1.041°。