基于随机p-鲁棒优化的国家血液战略储备库选址-库存模型

周愉峰，李 志，刘思峰

(1.重庆工商大学重庆市发展信息管理工程技术研究中心，重庆 400067; 2.南京航空航天大学管理科学与工程博士后流动站，江苏 南京 210016)

1 引言

大地震、特大恐怖袭击等严重突发事件可能导致大量人员伤亡，短时间内造成血液需求骤增。血液属于易腐物品，其采集、检测、制备、储存、使用等要求严格、无法即采即用，且难以被其他物品替代。再加上血液供应关系到伤员的生命健康安全。因而完善血液储备体系对于灾后抢救、降低社会恐慌，提高血液保障水平等方面具有重要意义[1]。

目前，我国尚无统一的国家血液战略储备库体系。而以往的救灾实践又对国家层面的血液战略储备库建设提出了迫切要求。因此，国家血液战略储备库的建设问题在理论与实践中亟待解决。当前，一些研究者初步设想在若干省级血液中心建立国家血液战略储备库[2-3]。例如，吴卫星等[4]建议在人口密度较大的区域设立1到3个由国家卫生部控制的国家血液战略储备单元。郑忠伟等[1]提出在我国6大区域建立若干个国家层级的应急血液储备库，并执行血液定期轮换策略。黎城等[5]提出以省为单位储存红细胞，构成国家血液储备单元。沈红艳[3]提出以全国七大军区驻地血液中心为基础，建设国家血液储备库。

上述文献均从定性角度，探讨国家血液战略储备库建设的可行性和必要性等问题，缺乏定量研究。鉴于此，孟超[2]考虑调配时效和可靠性目标，研究了国家血液战略储备设施选址-分配问题。但孟超[2]没有考虑库存因素。由于大规模涉血灾害的发生概率非常小，若一味追求灾时血液保障时效最优而完全忽略成本因素，将产生极其高昂的日常运营成本。因此，国家血液战略储备库选址应该考虑日常库存运营成本，建立预算约束条件下的应急调配时效最优化的选址-库存问题模型(Location-inventory problem，LIP)。此外，孟超[2]假设国家血液战略储备库在现有省级血液中心基础上设置，因而可充分利用既有资源而无需考虑设施建设成本。该假设显然与现实不符。原因在于各省血液中心的库存容量是基于日常需求设计的。设为国家层面的战略储备库后，灾时爆炸性增长的血液需求会导致血液中心储备能力受到限制。因此，须对选定的血液中心进行改扩建处理，并在模型中考虑改扩建所涉及的固定投入成本及库存运营成本增量。因此，本文集成库存决策，考虑预算约束与系统及时度目标，在孟超[2]的基础上进一步研究国家血液战略储备库LIP模型。

与本研究相关的问题主要有两类。第一类为应急设施选址问题(Facility location problem，FLP)及采供血机构选址问题。有关应急设施选址问题的研究较多，例如，张敏和张玲[6]研究了基于失效情景的应急设施选址模型。近年来，以采供血机构为背景的FLP研究也引起了研究者们的关注。Zahiri等[7-8]分别从静态与多阶段优化的角度研究了固定采血点与流动献血车的选址-指派问题。Sha Yue和Huang Jun[9]建立了震后应急血液FLP模型。周愉峰等[10]以血站为例研究了应急物资储备库选址的可靠性p-中值模型。Chaiwuttisak等[11]建立了两类采血服务设施的选址以及与医院、血站之间的指派优化模型。Zahiri和Pishvae[12]考虑血型兼容与需求不确定性，建立了血液供应链网络设计模型。但这些研究一般强调受灾点满意度或对需求的响应速度等因素，很少同时考虑设施的日常运营成本与灾时响应速度，且没有集成库存问题。第二类为选址-库存问题(LIP)。以往的LIP文献大都研究的是一般物资在常规条件下的集成决策问题。例如，Sadjadi等[13]研究了三级供应链网络设计中的随机需求LIP。Zhang Zhihai和Unnikrishnan[14]研究了闭环供应链中的随机需求LIP。Li Yanhui等[15]研究了闭环物流系统中带第三方物流商的LIP。Vahdani等[16]研究了三级供应链网络设计中的LIP。Diabat等[17]研究了需求与提前期均不确定的LIP。这些研究没有考虑血液制品特性与血液保障的应急特性。有关应急设施LIP的研究较少[2]，但一些文献基于随机规划[18-19]、鲁棒优化[20]、可靠性优化[21]等方法研究了LIP，可为应急条件下的LIP研究提供借鉴。

由于血液产品特性以及应急血液保障特性的存在，使得国家血液战略储备库选址-库存问题需要考虑众多因素，例如：储备库日常运行成本与灾时响应速度的均衡、血液制品的多品种性、灾后应急血液需求的多阶段性、日常需求的随机性、储备库建立后的设施容量限制、改扩建后的库存状态变更、应急条件下的协同定位等因素。上述因素在以往的应急FLP与LIP研究中没有同时考虑，因而需在国家血液战略储备库LIP问题中予以扩展研究。同时，考虑到多情景涉血灾害发生的不确定性，本文引入p-鲁棒,构建了一个考虑多情景、多血型、灾后需求多阶段、日常需求随机、设施有容量限制及协同定位、有预算约束的国家血液战略储备库LIP模型。针对模型性质，设计了求解问题的两类亚启发式算法：遗传算法(Genetic algorithm，GA)与免疫优化算法(Immune optimization algorithm，IOA)，并通过仿真算例验证了所提模型及算法的有效性。

2 国家血液战略储备库选址-库存问题的随机p-鲁棒优化模型

2.1 问题描述

设置国家血液战略储备库的目的是在灾时为伤员提供快速有效的血液保障。因而以灾时的系统响应时效最快来体现这一目标。由于涉血灾害发生的突发性和不可预见性，应急血液需求难以事先确定。为此，采用情景分析方法来描述应急需求。假设所有情景均只有一个需求点，即任何情景下只有一个省份发生大规模涉血灾害。引发大量应急血液需求的突发事件主要有大规模地震与特大恐怖袭击。在这些突发事件中，应急血液需求具有明显的阶段性，可分为紧急救援期和救援中后期两个阶段。灾害发生后的72小时为紧急救援期，即两个阶段的间隔时间为3天。灾时的应急血液需求与救援期所处阶段密切相关。应急条件下由于需求量骤增，储备库容量受到限制，每种血液制品在出库后需要进行库存补充。由于灾时采集储备能力受限与需求增长，为了保障受灾点的血液供应，允许协同定位，即允许一个需求点同时由多个储备库提供应急血液需求。

由于大规模涉血灾害发生的概率很小，因而不能无限追求应急系统响应速度，必须考虑设施在常规条件下的日常运营成本，即考虑预算限制。为了最大限度的利用既有资源、降低成本，选择若干省级血液中心进行改扩建，而非在新址上全新建设。因此，须考虑改扩建的固定投入成本，以及库存状态变化引起的日常运营成本增量。省级血液中心被选建为国家血液战略储备库后，需大量增加各种血液制品的储备量以应对将来可能发生的突发事件。由于血液只能通过人体采集，得来不易，且保管周期有限。为了避免血液制品的大量过期报废，在平时需对库存进行轮换更新，因而省级血液中心被选建为战略储备库后，其库存系统会发生变化。常规条件下，省级血液中心日常需求量随机，可根据各地的历史数据拟合成一定的概率分布。

综上，问题可以被描述为一个考虑多情景、多阶段不确定应急需求、随机日常需求、多血型、有容量限制、有预算约束及协同定位的国家血液战略储备LIP。要解决的问题是：应该建立多少个储备库？建在哪里？如何对应急血液需求点与储备库进行指派？如何分配应急血液需求？如何进行日常库存决策？

2.2 符号说明

2.2.1 参数

I为需求点集合，即每个省级行政区；i∈I；

J为候选地集合，即现有的省级血液中心j∈J；

N为应急血液需求阶段集合；n∈N，n=1,2；

K为血型集合；k∈K；

tsn,n+1为相邻应急需求阶段的时间间隔；

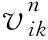
Capjk为候选地j对k型血的储备能力上限；

β为库存补充系数；

L为提前期；

FB为建立国家血液储备库的预算；

hjk为储备库j中k型血的单位库存持有成本；

c为单位运输成本；

dij为需求点i与候选地j之间的距离；

Ti为需求点i的应急需求调配时限；

tij为需求点i与候选点j之间的应急血液调配时间，tij由运输时间，需求点的接收耗时tp和候选点调剂准备耗时tb构成，即tij=dij/Vij+tp+tb；

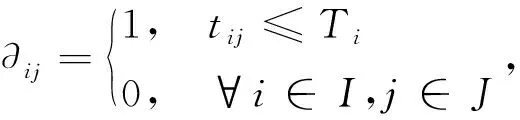
χ为规划期长度；

θ为与库存成本相关的权因子；

λ为与轮换更新成本相关的权因子；

fj为血液中心j改扩建为国家血液战略储备库的固定投入成本；

sjk为储备库j对k型血的安全库存保有量；

M为一个大的正数。

2.2.2 变量

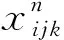
Xj表示在j地建立储备库时为1，否则为0

Sjk为储备库j中k型血的库存定至点

Qjk1为候选地j未建储备库前对k型血的采血批量

Qjk2为候选地j被建为储备库后对k型血的采血批量

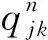
2.3 库存成本分析

为了应对未来可能发生的应急需求，选择对现有的若干省级血液中心进行改扩建，并固化增持一部分安全库存sjk。此时，原有的一些库存参数，包括储库存容量、安全库存，血液采集批量等发生了变化。因而需考虑建设国家储备库所支付的变动成本，包括：改扩建的固定投入成本，由改扩建引发的新增库存持有成本，新增安全库存持有成本及新增血液轮换更新成本。

(1)选作战略储备库之前的运营成本分析：

战略储备库的日常库存控制参数可表示如下：

安全库存：

(1)

式(1)中，zjk为储备库j中k型血的血液保障水平系数。

订货点：

(2)

平均库存：

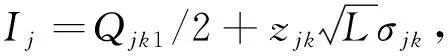
(3)

j地未设为战略储备库时的日常周转库存成本可以表示为：

(4)

式(4)，TPjk为j地两次连续订购的时间间隔：

TPjk=Qjk1/μjk,∀j∈J,k∈K

(5)

假设血液本地轮换成本为v(Qjk1)，令：

v(Qjk1)=gj+ajQjk1,∀j∈J,k∈K

(6)

式(6)中gj表示血液固定轮换更新成本；aj表示血液可变轮换更新成本。

对式(4)除以TPjk可以得到成本率的表达式：

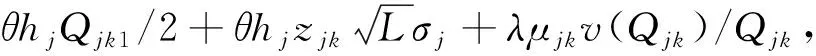
(7)

对式(7)中Qjk1求导，等于0，得到：

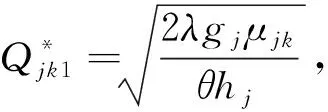
(8)

则j地未建战备库前的运营成本可以表示为：

(9)

(2)选作战略储备库之后的运营成本分析:

通过设置安全库存sjk以保障灾时的应急需求，为此，相应的库存控制参数需重新定义：

安全库存：

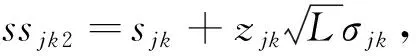
(10)

订货点：

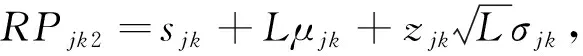
(11)

库存定至点：

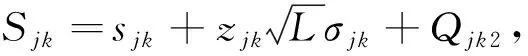
(12)

平均库存：

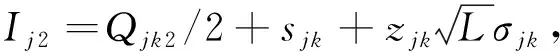
(13)

j地设为战略储备库后的周转库存成本为：

(14)

式(14)除以TPjk2得到成本率的表达式：

+λμjkv(Qjk2)/Qjk2,∀j∈J,k∈K

(15)

建为储备库后，灾时应急需求剧增，血库容量受限。此时，不能再用求导的方法计算最优血液采集量。为此，设置两个约束来处理应急血液采集量Qjk2。

约束(16)用来处理最大采集量。 假设储备库j对k型血的最大可采集量用Qjk2max表示，则

Qjk2≤Qjk2max,∀j∈J,k∈K

(16)

约束(17)为候选储备库的服务水平约束。假设δ为违背库存容量约束的最大概率，SDjk(LTj)为提前期内的随机需求量。采用机会约束规划处理服务水平的满足率：

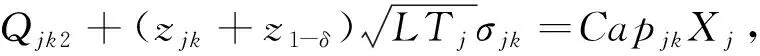
(17)

在此随机约束中，允许达到100%的服务水平。

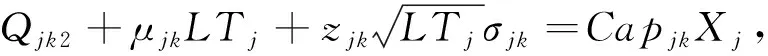
(18)

同时，为了保证安全库存保有量sjk也满足储备库已开放的前提，将成本率的表达式(15)改写为：

+λμjkv(Qjk2)/Qjk2,∀j∈J,k∈K

(19)

因此，在j地由于建设战略储备库所引起的新增成本为：

(20)

2.4 模型构建

至此，可建立LIP模型MP1：

(21)

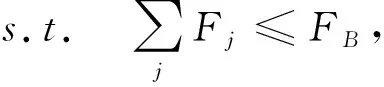
(22)

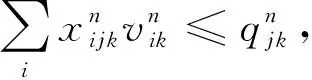
(23)

(24)

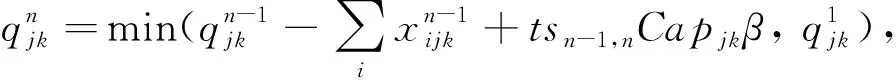
(25)

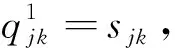
(26)

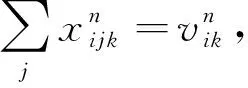
(27)

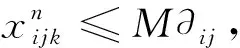
(28)

(29)

(30)

Qjk2≤Qjk2max,∀j∈J,k∈K

(31)

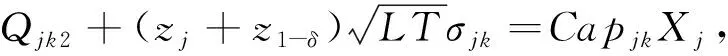
(32)

Xj∈{0,1},∀j∈J

(33)

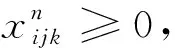
目标(21)表示灾时的加权需求时间最短，用来表示设施网络的系统及时度。式(22)为预算约束。约束(23)表示任意储备库的任意血液制品在任意阶段的供应量不能超过可用的最大库存量。约束(24)表示候选地在任意需求阶段开始时的最大可用库存量不超过安全库存保有量与储备能力上限。式(25)为每阶段开始时最大可用库存量的表达式。式(26)为灾害情景发生时最大可用库存量表达式；式(27)表示应急血液需求不出现短缺。约束(28)为应急调配时间限制。约束(29) 表示血液调配只能在已经设立的储备库进行。式(30)为非负约束。式(31)为血液采集量上限约束。约束(32)表示应急血液储备必须在开放储备库进行，同时必须满足血液保障水平。约束(33)为0-1整数变量约束。

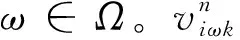
确定情景下的随机优化可产生目标值最优的解, 但是在特定的情景中可能表现很差[22]。为了规避这种情况，建立国家血液战略储备库LIP的随机p-鲁棒优化模型。

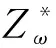
由模型MP1可知，确定情景ω下，国家血液战略储备库选址-库存问题的模型MP2为

MP2：

(34)

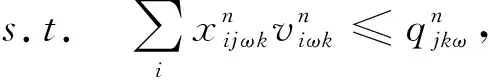
(35)

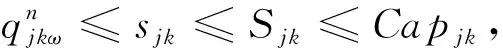
(36)

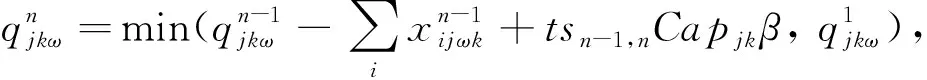
(37)

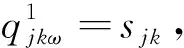
(38)

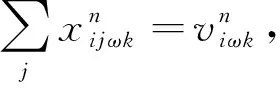
(39)

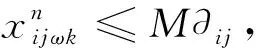
(40)

(41)

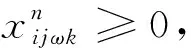
(42)

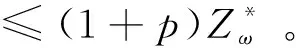
MP3：

(43)

(44)

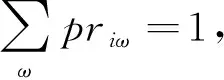
(45)

式(44)为p-鲁棒优化的约束条件。式(45)表示任意需求点所有需求情景的概率之和为1。约束(22) 、约束(31) -约束(33)与模型MP1、MP2相同，约束(35)-(42)与模型MP2相同。

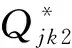
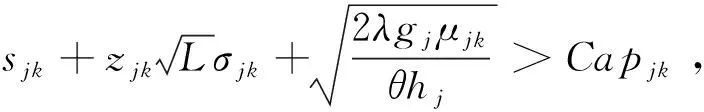
故性质1得证。

性质2：令Ii={j|∂ij=1,∀j}表示在时限约束内可对需求点i提供服务的储备库集合。按应急血液调配时间tij,j∈Ii升序排列Ii内的所有储备库，得到{j1,j2,…jr|j∈Ii}。若储备库已选定，则最优的分配方案为按照j1,j2,…jr的顺序依次对需求点i提供血液保障。

证明：由于任意情景均不会有两个以上省份同时发生大规模涉血灾害，所以若开放储备库给定，则系统总成本也固定。此时，将需求点i指派给最近的持有救灾库存的储备库能提高供应速度。故性质2得证。

3 求解算法

MP3也为NP-hard问题，难以精确求解。为此，设计一种0-1编码的遗传算法对模型进行求解。遗传算法具有并行计算能力强，收敛速度快，不易陷入局部最优等特点，对于解决复杂组合优化问题具有突出优势。同时，为了验证所提遗传算法的性能，另外设计了一种免疫优化算法，并在后文对这两种经典进化算法进行比较分析。

所设计的遗传算法流程描述如下：

①编码/解码

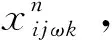
(46)

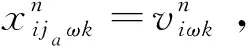
否则：

(47)

②初始化种群

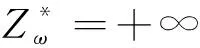
③适应度评价

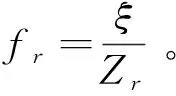
由于种群中可能存在非可行解，需对不满足约束的染色体进行惩罚。

设lost为某条非可行解染色体r的应急血液需求短缺量，则：

(48)

然后对需求短缺、预算超支、p-鲁棒性三个约束进行惩罚，目标值Zr可以表示为：

(49)

式(49)中，第2项表示对血液短缺量进行惩罚，第3项表示对预算超支的惩罚,第4项表示对p-鲁棒约束未满足的惩罚。κ，π，γ分别为染色体需求未满足、预算超支、p-鲁棒约束未满足的惩罚因子，应为较大的正数。

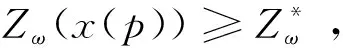
④选择、交叉和变异

采用轮盘赌选择，并采用精英保留策略将每代的最优个体保留进入下一代种群，以加快收敛。采用单点交叉和互换变异操作。

⑤终止条件

达到最大迭代代数时，停止计算并输出结果。

4 算例分析

以中国大陆地区31个省级血液中心作为储备库的候选建设点，31个省级行政区为需求点。省级血液中心的日常需求分布见孟超[2]和沈红艳[3]。在破坏性地震、大规模恐怖袭击等典型涉血灾害下，灾后应急血液需求具有明显的阶段性，可分为紧急救援期和救援中后期两个阶段。灾害发生后的72小时为紧急救援期，即两个阶段的间隔时间为3天。临床输血抢救大多发生在紧急救援阶段，后期需求趋缓，因而假设中后期血液需求量为紧急救援阶段的70%[2]。考虑3种情景，情景1为最坏情景，情景2较严重，情景3程度最轻。根据中国人口危险性等级分布图及对照表得到31个省级行政区(需求点)的相对灾害发生概率[24-25]。假设“5.12”地震为四川省的最坏情景。“5.12”期间成都血液中心关键救援期内紧急调运的3类血液制品红细胞、全血、血浆分别为4235.5U、504U、1780.75U。以此数据为基准设置情景1的总需求量。假设情景2和3的需求量分别为情景1的50%和20%(灾害越严重，临床血液需求量越大)。一般情况下，某个需求点伤员的血型比例分布大致与当地总人口的血型比例相同，因而4种血型血液制品的需求量也按照当地总人口的血型比例来分配产生。各省总人口血型比例分布、省级血液中心编号与经纬度分布见周愉峰[24]。候选地的储备能力上限系数见孟超[2]。库存补充系数为0.3/天[2]。需求点的应急血液接收耗时，各候选地调剂准备耗时均为3小时，应急调配时限为8小时。运输速度为800km/h，运输时间通过运输距离除以运输速度计算。运输距离根据31个城市血液中心的经纬度进行计算[3，24]。单位运输成本为10元/吨公里，库存持有成本为10元/单位。任意血液制品的库存服务水平zjk为1.96。鲁棒概率参数p=0.03。

遗传算法参数设置如下：最大迭代次数为Maxgen=500，种群规模popsize=100，交叉概率pc=0.9，变异概率pm=0.1。3个惩罚因子κ=π=γ=100000。基于Matlab®2010a平台，在Intel Pentium(R) G3260T 2.90GHz CPU，64位操作系统，4G RAM的PC机上运行程序。根据不同预算值FB，设计6个算例，计算结果见表1(取5次运算的最优值作为最终结果)。图1为算例5的算法收敛曲线。表2为开放储备库的采血批量(算例5)。图2、图3分别为算例5(情景1)和算例6(情景2)下的选址-分派方案。计算结果表明：①系统及时度与预算投入正相关，但及时度的改善速度随着预算的增加而下降：在预算投入较少时，少量增加成本可以大幅度提升系统及时度；当预算增加到一定程度时，再增加投入引起的系统及时度目标改善非常有限(例如，算例5与算例6相比，成本增加14.29%，系统及时度目标改善1.53%；算例1与算例2相比，成本增加66.67%，系统及时度目标仅改善1.73%)。②少数情景下的鲁棒模型对应的目标值小于确定性模型的最优值，但两者的相对偏差较小(最大偏差≤1.08%)。因而可得出结论：虽然p-鲁棒解不能在所有情景下实现最优目标值, 但适用于所有情景，与确定性模型最优值的差距很小。因而p-鲁棒优化可降低不确定性风险。③血液战略储备库布局呈现出西部较稀疏、中东部较稠密的特征。在库存决策上，西部地区建立的储备库采血批量较小，中、东部地区储备库采血批量较大。主要原因可能在于西部地区地广人稀，血液供需规模较小，导致西部地区设施点数量、指派规模、采血批量等低于中、东部地区。

为了测试遗传算法的性能，与免疫优化算法进行比较。在此，设计两组算例。第1组算例基于我国大陆地区31个省级血液中心与省级行政区的数据，根据不同预算值FB，设计6个算例。第2组算例为6个不同规模的模拟算例。最大规模为60×60节点算例，节点生成规则为：在当前31个节点的基础上再生成29个随机节点，纬度在[20, 45.77]之间随机均匀产生，经度在[87.57,126.68]之间随机均匀产生(其中，20，45.77分别是31个省级血液中心纬度的最小值与最大值；87.57，126.68分别是31个省级血液中心经度的最小值与最大值)。其他参数在31节点算例参数的最小值与最大值之间随机均匀产生。其他规模算例的节点则在60节点中随机抽取。6个不同规模算例的预算参数FB分别设为：1000000，2000000，3000000，4000000，45000000，5000000；库存补充系数设为0.1/天。其他参数设置同上文。由表3与表4的12个算例可知，在计算精度上，遗传算法在7个算例上的表现较好，免疫优化算法在3个算例上的表现更优，另外2个算例结果相同。而在计算效率上，遗传算法明显优于免疫优化算法。因此本文提出的遗传算法具有较好的性能。

表1 6个算例的计算结果

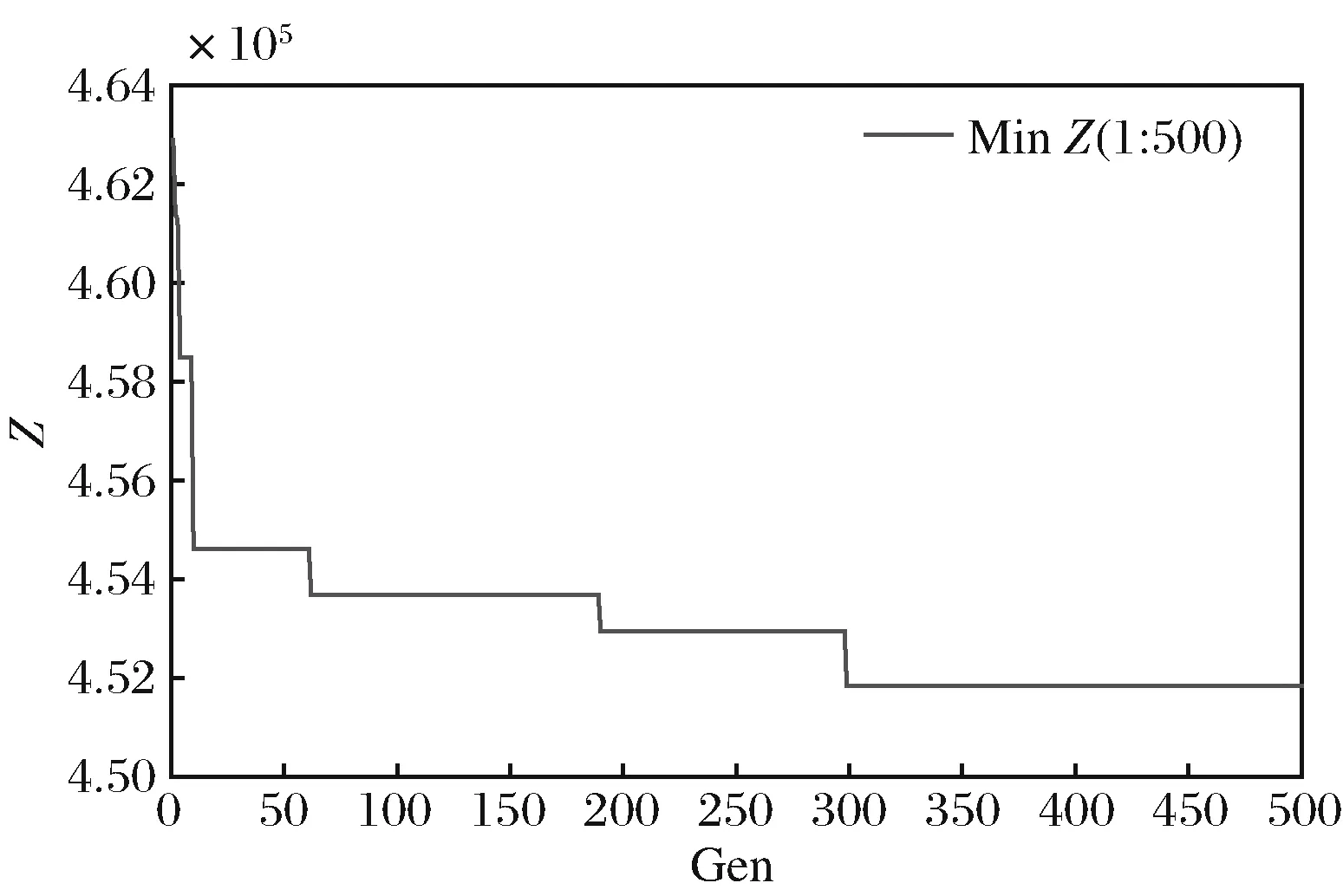
图1 遗传算法收敛曲线(算例5)

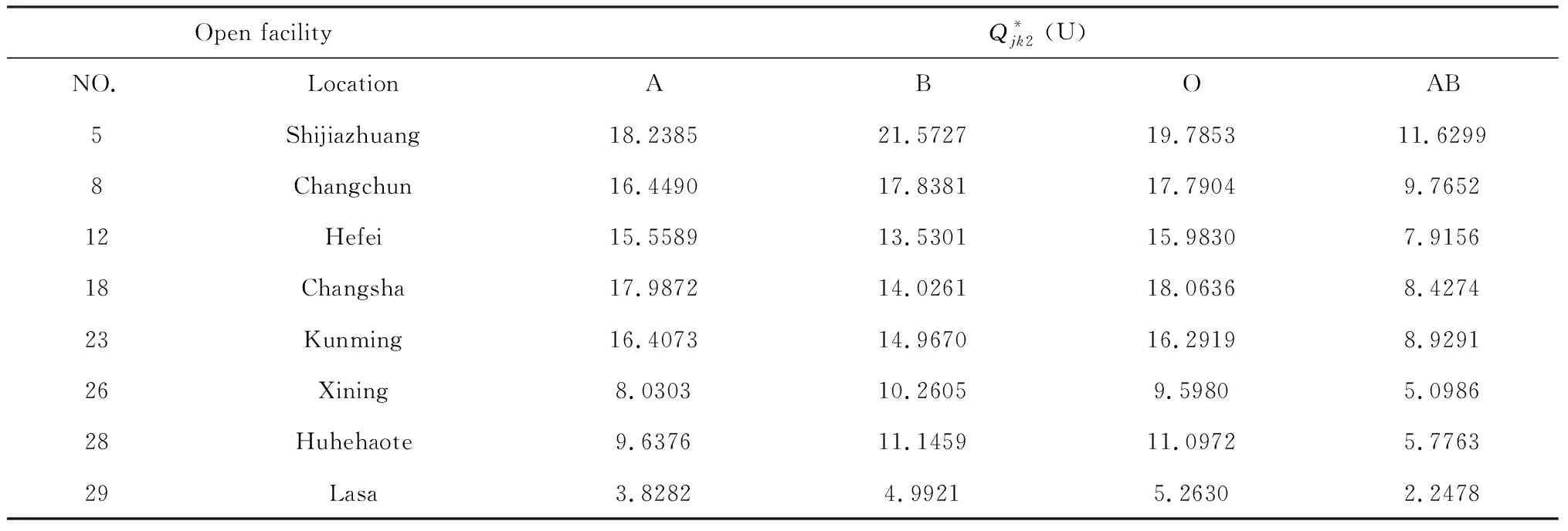
表2 已选储备库各型血的采血批量(算例5)

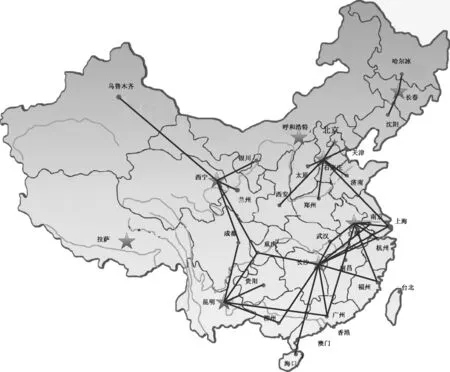
图2 算例5下的选址-分派方案(情景1)

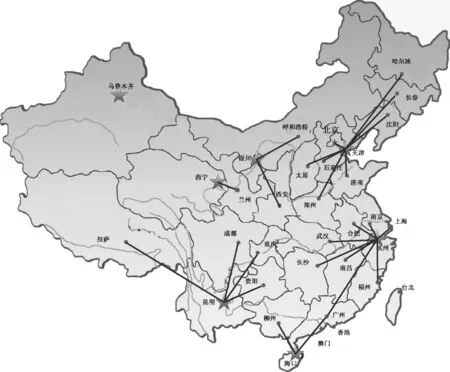
图3 算例6下的选址-分派方案(情景2)

此外，表3、表4的结果同样说明了p-鲁棒优化可降低不确定性风险(平均偏差≤1.12%)。

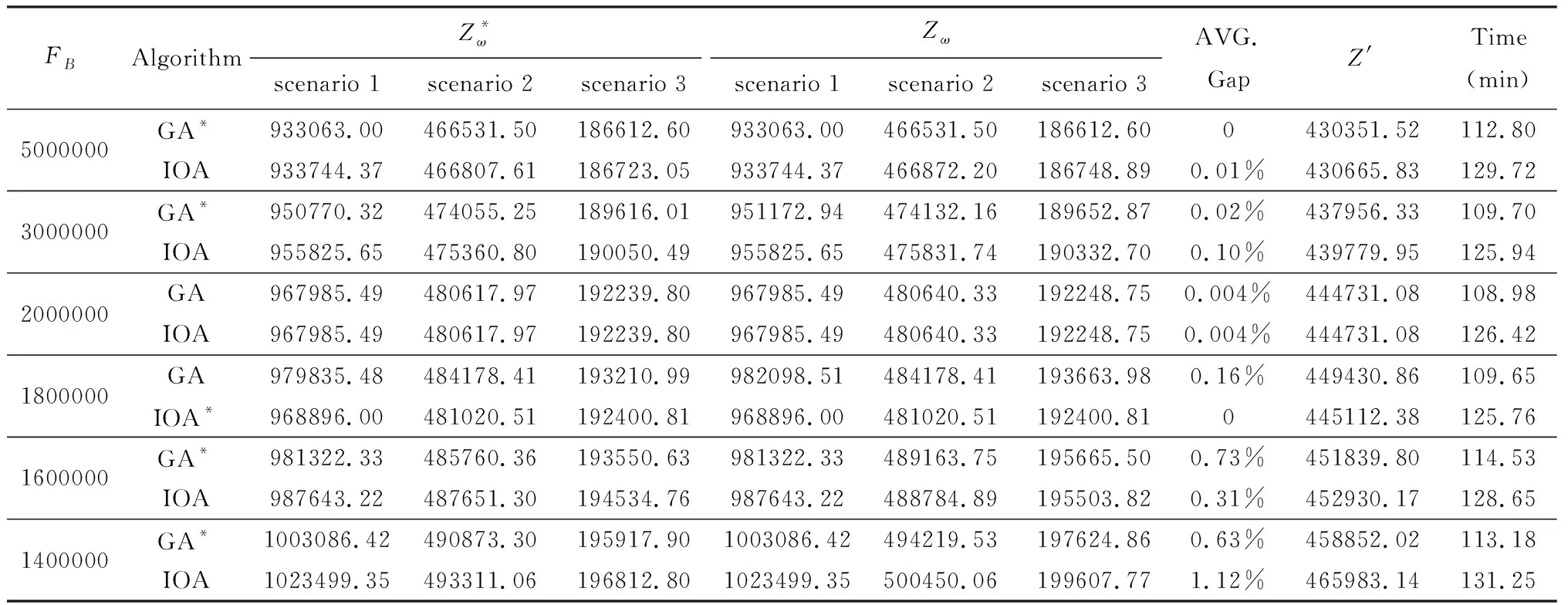
表3 遗传算法与免疫优化算法性能对比(31节点算例)

表4 遗传算法与免疫优化算法性能对比(规模分析)

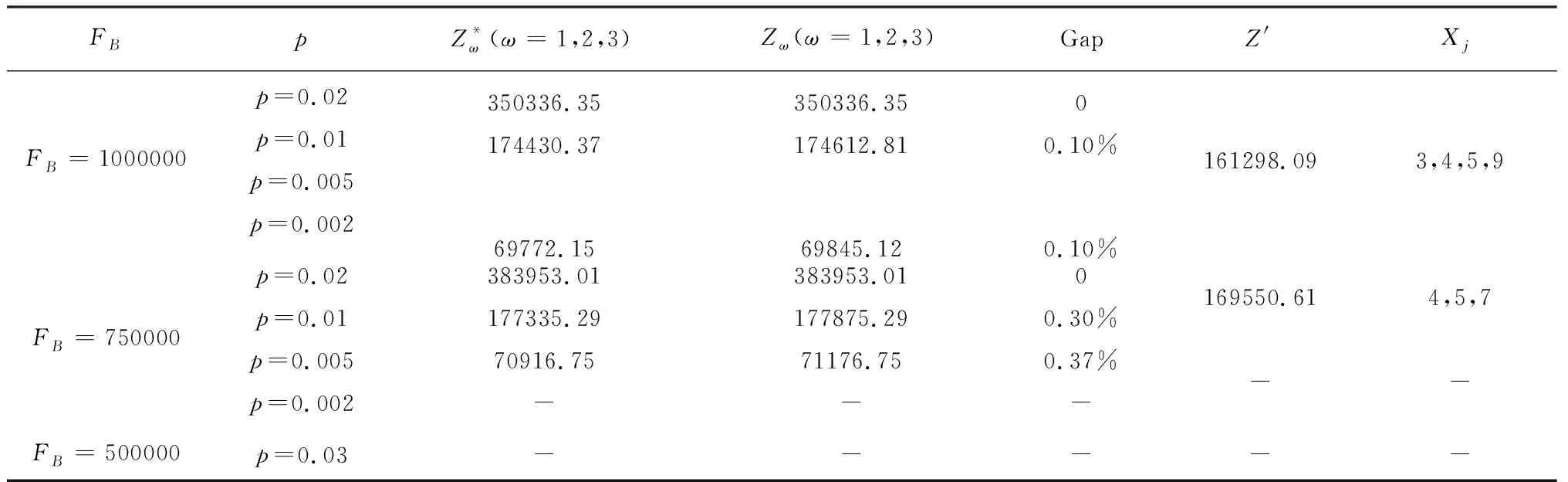
表5 鲁棒概率参数p的敏感性分析

为了进一步分析遗传算法效率，给出算法的计算复杂度函数。设|I|、|L|、|K|、|Jo|分别表示需求点数量、情景数量、血型数量、开放储备库数量。则一次迭代中：初始化的算法复杂度为O(popsize)；适应度评价的算法复杂度为O(popsize×|I|×|L|×|K|×(2+|Jo|)；选择、交叉和变异的复杂度为：O(6×1/2×popsize)；其他操作为单步，可不计。因此，一代计算过程的算法复杂度Com为：

Com=[O(popsize)+O(6×1/2×popsize)]+O(popsize×|I|×|L|×|K|×(2+|Jo|)≈O(popsize×|I|×|L|×|K|×|Jo|)

(54)

因为|Jo|的理论最大值为|I|，则复杂度可进一步简化为：

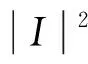
(55)

最后对鲁棒概率参数p进行敏感性分析(表5)。为了便于分析结论，取10*10节点算例进行试验(小规模算例更易得到全局最优解)。结果表明：预算参数FB足够大时，参数p的取值对解的影响小。反之，FB较小时，p的取值对解的影响较大。原因在于FB越小，模型限制越强，可行解空间越小，对鲁棒概率参数p的限制也越强。

5 结语

国家血液战略储备库的建设问题亟待解决。以应急血液保障及时度最高为目标，考虑多情景不确定需求、多血型、多阶段、设施容量限制及协同定位等灾时应急特性，同时考虑日常运营成本与预算约束，建立了一个国家血液战略储备库LIP的随机p-鲁棒优化模型。采用非线性混合整数规划方法描述该模型。并基于模型性质，设计了一种遗传算法对问题进行求解。通过多组算例验证并与免疫优化算法进行对比, 证明了所提模型和算法的有效性。本文给出了若干组不同预算值下的选址-库存决策方案。实践中，决策者可根据预算需求及偏好，选择合适的选址-库存决策方案。

研究结论及启发是：①系统及时度与预算投入正相关，但及时度的改善速度随着预算的增加而大幅下降。因而需要根据实际情况，权衡预算投入与系统及时度目标。在投入较小时，可以少量增加预算，以大幅度提高应急血液保障的效率；反之，若预算过大，可以考虑适当缩减投资，在应急血液保障效率损害很小的前提下大量降低成本，②虽然p-鲁棒解不能在所有情景下取得最优值, 但与确定性情景模型最优值相差不大。由于国家血液储备网络设计问题属于战略性决策问题，因而必须考虑网络构建的鲁棒性，以降低不确定性风险。

本文以国家血液战略储备库为研究对象，实际工作中，可对模型稍作改进，应用于同样存在多情景多阶段不确定应急需求与日常随机需求、多产品、有容量限制及协同定位、改扩建与预算约束等特性的易腐品(药品、粮食等)应急物资储备库LIP中。进一步研究可以考虑血液的新鲜度因素，扩展本文提出的LIP；也可考虑设施中断风险等因素，对选址-库存模型进行可靠性优化。