随商的订购-定价联合决策问题

吉清凯,胡祥培,郭 强,赵 达

(1.海南大学经济与管理学院,海南 海口 570228；2.东南大学经济管理学院，江苏 南京 211189；3.大连理工大学管理与经济学部,辽宁 大连 116024；4.海南大学科研处，海南 海口 570228)

1 引言

供应链运作面临许多风险，除了常见的随机需求风险外，随机供应的风险也越来越突显。据著名咨询公司McKinsey与Accenture近年的调查，对众多制造企业而言，供应风险管理已成头等大事，许多企业甚至认为供应稳定性比成本控制还要重要[1]。因此，随机供应与随机需求条件下的供应链管理已成为业界与学术界共同关注的热点。其中，随机供需条件下的订购-定价决策模型是供应链管理领域的前沿研究方向之一，近年在国内外顶级期刊及会议上时有相关的论文发表。对于许多生产创新型消费类电子产品(Innovative Consumer Electronics，ICE，如智能手机)的装配式制造企业而言，随机供应更加常见，同时，在零部件互配性的作用下，随机供应的风险将被放大。并且，因为ICE产品具有生产周期长、生命周期短、热销周期短和需求不稳定的特点，所以订购与定价是这类装配商的生死攸关的决策，如何在随机供应与随机需求的条件下协调订购与定价从而使得供需匹配是其迫待解决的难题。在这一背景下，随机供需条件下装配商订购-定价的决策模型研究具有重要的理论意义与实际意义。

ICE产品往往由成百上千种零部件组成，其中涉及诸多新技术、新设计与新工艺，在生产制造过程中将不可避免地遇到诸如次品率过高、特殊材料不足、精密设备出错等许多麻烦，零部件供应商的产能因此表现出随机性，从而导致零部件与最终产品供应的随机性。例如，苹果手机iPhone 5曾因为其屏幕供应商在生产in-cell触控屏时遇到麻烦而出现缺货，HTC One Mini也曾因机壳短缺导致新品发布大幅延迟而错失销售良机。对于随机供应风险，装配商不愿用囤积库存来应对，毕竟在高新制造行业中库存呆滞的风险更高，尤其是ICE产品中包含许多不通用、易过时的零部件，呆滞库存意味着极大的沉没成本。因此，装配商更多地寄望于科学的零部件订购决策与产品定价决策来平衡供需。但当需求与供应都具有随机性时，定价与订购的关系变得复杂。尽管已有不少研究考虑了需求或供应随机情况下的订购与定价模型[2]，但其并不能完全适用于生产ICE产品的装配系统，仍存在有待改进之处：如以往有些研究比较局限地考虑包含两种零部件的系统，或者只假设某一个零部件的供应具有随机性[3]；又或者预先假设订购策略的结构而寻找最优参数[4]，对于订购与定价的最优决策本身的刻画不够充分等等。因此，目前仍需在前人的基础上，针对随机供需下一般化的装配系统(指包含n种零部件，且每一零部件的供应都具有随机性)，为其中的多零部件订购决策、组装决策及最终产品定价决策建立相应的模型，刻画其最优的订购-定价策略，为装配商的管理实践提供科学的决策支持。由于本文所研究的装配系统具有多重随机性与零部件互配性，这将使得n种零部件订购量间的最优比例关系变得不清楚，零部件订购量与最终产品定价的交互影响也变得复杂。

针对上述难题，本文建立关于零部件订购与最终产品定价的随机非线性约束规划模型，根据系统特性降低模型的维度，然后综合利用分解法、逆推法与约束极值的处理方法刻画出最优的订购策略与定价策略，并对随机供应与需求的影响展开分析，为装配商提供科学的辅助决策工具与有益的管理启示。

与本文相关的文献主要有两类：(1)生产-定价或订购-定价联合优化模型，(2)随机供需下的生产或订购决策模型。第一类研究始于Whitin[5]，其刻画了均匀分布需求下的最优生产/订购与产价的联合决策，后来众多学者对一般分布情况下的最优决策进行了细致的刻画[6]，并从多种角度(系统特征与产品特性等)做了大量的扩展研究[7]：如李贵萍[8]基于前景理论进行研究报童定价-订购决策；段永瑞等[9]研究有限时域内部分缺货的变质品生产与定价联合决策，Yan Xiaoming与Wang Yong[10]研究随机产出下易逝品的订购-定价决策；Pan Wenting与So[3]研究包含两个零部件的系统，假设某个零部件具有随机产出，刻画订购-定价最优策略，等等。在第二类研究中，学者们着力刻画随机供需下各类系统的最优生产/订购策略，如Wang Yunzheng与Gerchak[11]研究同时存在不确定产能与随机产出时的单级系统，证明最优策略具有一种单临界点的结构；Hwang与Singh[12]研究各级产能都不确定且具有固定成本的多级串行系统，证明单周期中的最优策略是一种环环相扣的二临界值型策略；Hu Xinxin等[13]研究包含两个生产基地的分布式系统，刻画了最优的库存分配策略与生产策略；Erdem等[14]研究面对多个具有不确定产能的供应商的EOQ系统；Ji Qingkai等[15]刻画了随机供需下一般装配系统的最优生产策略；等等。还有学者假设系统按基本库存策略运行，寻求随机供需下最优的策略参数并考察系统的表现：如Bollapragada等[4]研究具有服务水平约束的装配系统，分析了最优服务水平与最优策略参数；Bollapragada等[16]通过数值分析研究不确定产能与提前期在一个实际的装配系统中的影响。此外，也有学者考虑各种针对随机供应的应对策略，如Wang Yimin等[17]比较了双源采购与流程改进(可随机地提高产能)的优劣，钱佳与骆建文[18]假设零售商面对的是具有不确定产能的主要供应商与产能充沛的后备供应商，研究订购量的分配以及对主要供应商的支持投入(如流程改进与知识输入等)决策；马士华与李毅鹏[19]建立信息共享或加班赶工及资源外包下多供应商间的横向协同模型；Xiao Yongbo等[20]研究装配系统中包含预先装配量、零部件预存量、追加装配量以及外包量的多阶段决策模型。

尽管第一类研究已经从多种不同的角度对生产/订购与定价的联合优化进行了大量研究，但是其中涉及的生产/库存系统主要是单级或串行系统，与本文中的装配系统在结构上有本质不同。在装配系统中要考虑多个零部件的匹配，随机供需下的订购-定价联合决策将变得更加困难，Pan Wenting与So[3]做了初步的探索，但在模型通用性方面仍有较大的改进空间。第二类研究中关于装配系统的研究有四篇，它们与本研究的不同之处在于：Bollapragada等[4]关注的是某种库存控制策略的最优参数，Bollapragada等[16]用纯数值分析的方法研究提前期对装配系统的影响，而本文聚焦于建立解析模型、刻画最优的订购-定价联合决策；Xiao Yongbo等[20]关注的是组装产能不确定下两阶段的生产与外包决策，而本文是在Ji Qingkai等[15]的基础上，研究零部件产能不确定和最终产品需求随机条件下单阶段内装配商的零部件订购量与最终产品定价联合决策。综上所述，本研究将有助于丰富订购-定价联合优化与随机环境下装配系统运作管理领域的理论研究，且有助于管理者在随机环境下做出科学的订购与定价决策。

2 问题描述与假设

一个装配商在销售季前分别从n个供应商处购买n种零部件组装成一种产品进行出售，每一单位产品包含一单位的零部件i，i=1…,n。假设产品的随机需求依赖于产品价格p，记为D(p,)=y(p)，其中y(p)是关于p的单调减函数，是独立于p的随机变量，代表市场的随机扰动。令φ(·)与Φ(·)分别表示的概率分布函数与累积分布函数，令而表示失败率或故障率(Hazard Rate)函数。假设定义在支撑集[B,C]上，C>B≥0，若E()=1，则y(p)是需求的期望值。由于原料不足、生产工艺不精导致停机与返工等原因，零部件i=1…,n的产能Ki为随机变量，其累积分布函数与概率分布函数分别为Fi(·)与fi(·)，支撑集为(0,)。Ki(i=1…,n) 相互独立，假设装配商掌握每个供应商的产能信息。令ui表示装配商对零部件i的订购量，记u=(u1,…,un)。令wi为零部件i的批发单价，ci为生产成本，ciui时，故供应商i的最优计划产量而当qi≤ui时，所以因此，装配商订购ui单位的零部件i，但它实际收到的供应量为min{ui,Ki}。

表1 主要变量和参数符号说明

为便于分析，另做如下假设：

(A1)零部件与最终产品都不具有残值，其库存成本亦可忽略；

(A2)组装成本为零，或可认为其已从p中扣除；

(A3)若产出无法满足市场需求，则装配商仅承受相应的销售损失，而不存在额外的缺货惩罚成本；

(A4)装配商是区域性的垄断者，其零部件购买价wi,i=1…,n为外生变量。

事件发生顺序为：

(1)装配商对订购量u与产品价格p做出决策；

(2)供应商i根据计划其产量并进行生产配送；

(3)装配商收到零部件的实际供应量；

(4)匹配零部件组装成产品并满足需求。

因此，装配商的期望利润函数为

Π(u,p)=E[pmin{min{u1,K1},…,min{un,Kn},D(p,)

(1)

其中E表示关于Ki，i=1…,n的期望。装配商的目标是最大化其期望利润。

3 模型分析

当供应确定时，显然装配商应订购等量的零部件，否则因零部件不匹配只会徒增成本。在随机供应下，是否每个零部件的订购量仍应保持相等？引理1回答这一关键问题。

证明不失一般性，假设u1≤…≤un(否则重新编号)，则此时装配商的期望函数变为

Π(u,p)=E[pmin{u1,K1,…,Kn,

(2)

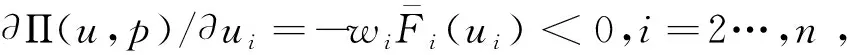
引理1说明：尽管产能不确定性可能导致各零部件的实际供应量不相匹配，但其订购量仍应保持匹配。其根本原因在于订购量不会对产能有影响，装配商所应做的就是按等比例订购，否则零部件供应量不匹配的可能性会更大。根据引理1，可用单一变量u表示装配商的订购量，则其期望利润函数可简写为

Π(u,p)=E[pmin{u,K,D(p,)

(3)

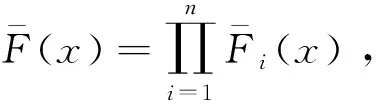
注意到当不存在任何供应能力约束时，装配商的问题退化为一个经典报童框架下的订购-定价模型[21]，如Petruzzi与Dada[21]中所用的方法，可定义z=u/y(p)为所谓的“库存因子”(Stocking Factor)，从而能够将订购决策u与p从E[min{u,y(p)}]这一复杂的关系中分离出来，有利于分析并最终刻画出最优的订购与定价决策。但在本章中，如(3)式所示，随机供应K的存在使得这一技巧不再适用，最优解的刻画变得更加困难。因此，下面分别求解给定任一可行价格与订购量时，相应的最优订购量与最优价格。

3.1 任一可行价格对应的最优订购量

(4)

或，等价地，

(5)

的唯一且有限的解。

证明将(3)式展开得:

对其求偏导有

u*(p)为一阶条件∂Π(u,p)/∂u=0的解。因

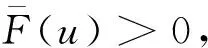
根据式(4)，利用隐函数求导法则，可得:

其中分子中第一项为正，第二项为负，du*(p)/dp的符号难以判定，可见随机需求下的最优订购量与价格的关系相当复杂。下面给出在特定条件下最优订购量与价格的单调关系。

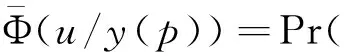
为供应量为u时供不应求的概率关于价格p的弹性[22]。

性质1当ξ(u*(p),p)≥1时，du*(p)/dp≤0，即最优订购量是价格的减函数。

证明因为ξ(u*(p),p)≥1等价于

根据以上两个不等式，可判定du*(p)/dp≤0。

ξ(u*(p),p)≥1的含义是：假设装配商拥有u*(p)件产品，若价格增大一个百分比，则出现供不应求的概率就降低超过一个百分比，因此价格上升时装配商应适当减少订购。此时，尽管随机供应的存在会使收货量随机地比订购量少，但装配商在订购时仍应适当减少订购量，否则收货量有可能高于装配商所需要的，反而出现供过于求的情况。

性质2 最优订购量u*(p)随着需求随机增大(即随机增大)而增大，随着零部件产能(Ki，i=1…,n)随机增大而增大。

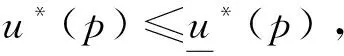
3.2 任一订购量对应的最优价格

对于任一零部件订购量，其对应的最优价格如以下命题所示。

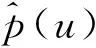
E[min{u,K,

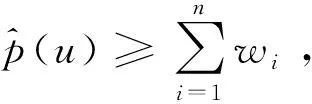
证明对Π(u,p)求偏导有:

记

其代表销售量对价格的反应，再令

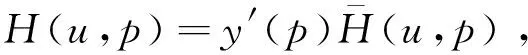
因此有

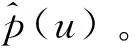
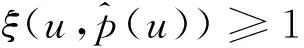
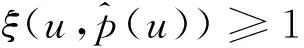
由性质1与性质3可见，在随机供需下，Π(u,p)不一定是次模函数，价格决策与订购决策不一定具有可替代性，调高价格不一定意味着要减少订购量，而增加订购量不一定意味着要调低价格。但在一般情况下(指ξ(u,p)满足递增性[22])，性质1与性质3中的结论仍成立。

3.3 最优订购-定价联合决策

上两节已经分别刻画给定价格p时的最优订购量u*(p)与给定订购量u时的最优价格p*(u)，但u*(p)与p*(u)只分别代表函数Π(u,p)的两条最优路径，联合最优解(u*,p*)仍未得知。因为u*(p)比p*(u)具有更为简单的形式，故本文沿着u*(p)这一最优路径寻找联合最优解。将u*(p)代入Π(u,p)，则装配商的问题变为：

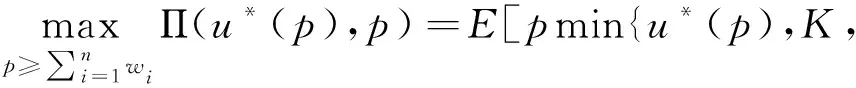
对Π(u*(p),p)求导有：

其中，第二个等号的得出用到了u*(p)的最优性，即∂Π(u*(p),p)/∂u=0。对dΠ(u*(p),p)/dp再求导有：

若同样假设py(p)为关于p的凹函数，则上式中后两项均为负，但第一项等价于

其为正项，故难以判断d2Π(u*(p),p)/dp2的符号，从而不能对dΠ(u*(p),p)/dp=0的解的唯一性下定论。但是，可根据以上分析得到如下命题。

命题3 最优订购-定价联合决策(u*,p*)满足以下条件：

(6)

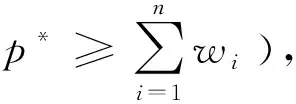
与式(6)中的第二个等式矛盾。

4 数值实验：随机供需的影响

在大量的数值实验中，上一章中已被严格证明的理论结论均得到验证，在此章不再赘述。本章的目的是通过数值实验来进一步直观地考察随机供需对最优订购与定价的影响。考虑n=2的装配系统，零部件批发价为w1=10。同样只考虑β>1即弹性需求的情况。需求随机因素不依赖于价格，并且服从均值为1的正态分布，即～N(1,σ)，1≫σ>0表示方差较均值小得多，从而取负值的概率几乎为零。此时E[D(p,)]=αp-β，代表装配商对需求的预测。令α=100，在以下算例中令β在{1.1,1.5,2.0}内变动以考察需求价格弹性的影响。

假设各零部件供应商的随机产能均服从Weibull分布，即Ki～Weibull(λi,κi)，i=1,2，κi∈+，λi>0，Ki的支撑集为[0,∞)。Ki的均值为λiΓ(1+1/κi)，方差为分布是可靠性工程领域常用的分布，用以描述一个系统或部件在某段时间内正常运行的能力。若用Weibull分布来描述关于“失败-时间”的变量，则其隐含着失败率与时间的幂数成比例关系，并且当形状参数κi>1时，表明失败率随时间递增。因为产能在很大程度上决定于生产制造系统的可靠性或失败率，所以用Weibull分布来刻画随机产能比较贴切。Weibull分布的概率密度函数严重依赖于形状参数κi，当κi较大时其概率密度函数具有单峰形状，可表明随机产能在单峰(代表最初的设计产能)的周围波动，比较符合实际情况。因此，在以下算例中，令κi=5，i=1,2(即两个供应商的初始设计产能相等，或者装配商从两个供应商处预订的产能相等)，只变化尺度参数λi以考察其影响。

(I)需求方差及需求弹性的影响

表2给出需求随机因素的方差变化而其它参数保持不变时最优解(u*,p*)及最优利润Π*的取值。其中，λ1=λ2=10，σ以步长0.01在[0.01,0.11]上变动，表格中数值根据宽度四舍五入取有限位小数列出。表中用上下箭头表示变量的上升与下降的变化趋势，δ的定义与前相同。

表2 σ变化时(u*,p*)及Π*的取值

观察发现：保持其它不变，若σ减小，则u*增大、p*减小、Π*增大，而δ的变化依赖于β。换言之，当需求随机因素的方差变小时，零部件订购量增大、最终产品价格减小、装配商获取的期望利润增大，但其对装配商利润的边际促进作用依赖于需求弹性。管理启示：在乘式需求下，需求方差VAR[D(p,)]=[y(p)]2σ，其是关于p的减函数、σ的增函数。当σ减小时，需求方差整体而言会减小，因此，装配商将降低价格以刺激需求并增加订购量。尽管装配商降低价格使得需求方差有增大的趋势，但总体而言，仍是随σ减小的表示对应σ的最优价格)，这保证了装配商利润随σ增大。在现实中，随着电子商务的盛行，越来越多创新型消费类电子产品厂商在网络上销售产品，并且它们往往为其即将推出的新产品策划预售或预订(Advance Selling/Booking，或Presale)的活动，尽管对于这种活动存在许多营销学上的解释，但其对于降低需求方差其实有一定的作用。这是因为预售/订能够预先锁定部分需求，并且通过网站数据统计能够进一步修正需求预测，降低需求估计的偏差。有些智能手机厂商在预售/订后降低价格(产品仍在热卖季度中)，尽管这种行为背后的原因可能包括价格竞争、产品关注度下降等等，但需求方差的下降或许是厂商降价的重要原因之一。

(II)产能均值与方差的交叉影响

图1给出零部件i的产能分布参数以步长1在[1,21]上变化而其它参数保持不变时最优解(u*,p*)及最优利润Π*的取值。其中，λ3-i=10，实线对应λ1固定而λ2变化时参数的取值，虚线对应λ2固定而λ1变化时参数的取值。

观察发现：对于i=1,2，保持λ3-i=10和其它参数不变，若λi增大，则u*增大、p*减小、Π*增大。并且，对比“λ1增大λ2不变”与“λ2增大λ1不变”两种情况发现，前者中的u*比后者中的小，而两种情况下的p*、Π*几乎一致。

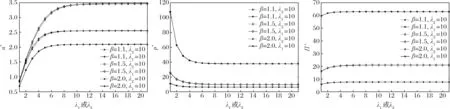
图1 λ3-i=10而λi变化时u*、p*和Π*的取值

管理启示：当λi变大时，期望产能变大，但产能也变得越来越不稳定。λi的增大可以解释为零部件供应商i将其业务再外包给多个二级供应商。此时，总体而言，零部件i的产能(供应量)均值变大了，装配商能够增加订购量、降低产品价格并最终获取更高利润。但是，二级供应商的增多也使得生产过程中面对的风险更大，从而导致零部件i的产能(供应量)变得越来越不稳定。对装配商而言，当供应商i之下的二级供应商数量逐渐增大时，零部件i的产能均值增大的好处逐渐被其产能方差增大的风险抵消，装配商能获得的利润增额越来越小。因此，在存在供应风险时，装配商有必要加强对二级供应商的管理。现实中许多装配商也越来越重视供应链的可视性。

以上结果的一个前提条件是λ3-i=10，即零部件3-i的产能相对已经比较充足(E[K3-i]≈9)。当零部件3-i的产能并不充足时(如λ3-i=1)，增大λi将出现极其不同的情况，如图2所示。

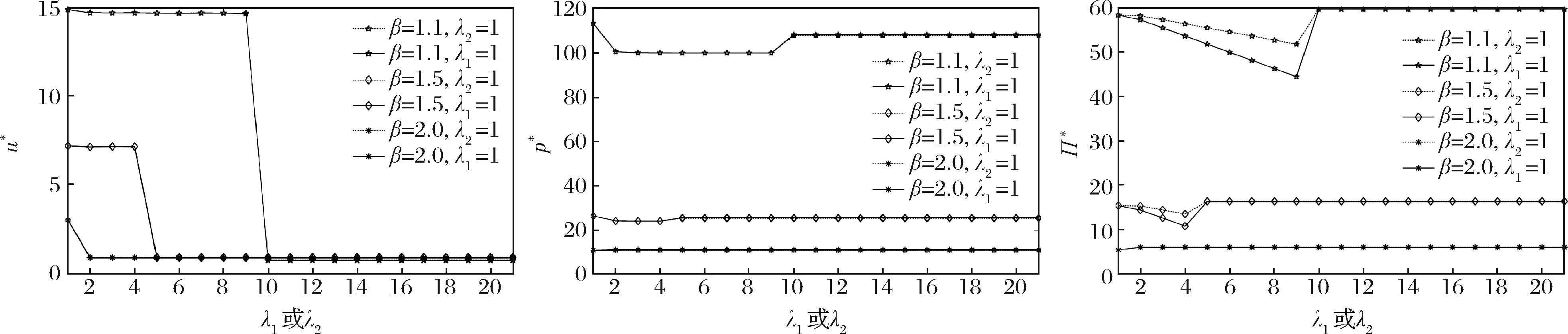
图2 λ3-i=1而λi变化时u*、p*和Π*的取值

观察结果：对于i=1,2，保持λ3-i=1和其它参数不变，若λi增大，则u*、p*与Π*非单调地变化。整体而言，u*有减小的趋势；当需求弹性较小时(β=1.1或β=1.5)，p*先减后增，Π*也先减后增，当弹性较大时(β=2.0)，p*先增后减，而Π*极其微小地增大。并且，对比“λ1增大λ2不变”与“λ2增大λ1不变”两种情况发现，前者中的Π*比后者中的大，而两种情况下的u*、p*几乎一致。当λi增大到某个临界点后，u*、p*与Π*的变化均趋于平缓。

管理启示：如前所述，λi的增大可以解释为零部件供应商i将其业务外包给多个二级供应商。此时，零部件i的产能(供应量)的均值与方差均变大了。但由于零部件3-i的产能并不充足，λi的增大反而使得零部件不相匹配的可能性增大。只有当二级供应商的数量多到一定数目后，即零部件i产能均值增大的好处超过其方差变大的坏处后，装配商才能够勉强获取更高利润，但增额极小。因此，供应商i的二级供应商数量增大对装配商而言并不一定有利。另外，当装配商要鼓励其零部件供应商发展二级供应商时，它应该鼓励那些具有产能瓶颈的供应商，否则有可能利润受损。

5 结语

本文研究随机供需下装配商单周期内的零部件订购与最终产品定价联合最优化决策模型，求解了给定价格时的最优零部件订购量和给定订购量时的最优价格，然后给出关于最优订购与定价联合决策的必要条件，最后分析了随机供需对最优决策的影响。研究发现：尽管存在供需随机性，装配商仍应按相等比例订购零部件，但其订购与定价决策受供需随机分布的影响，难以精确协调。最后通过数值分析说明：增大供应产能的均值(如通过投资新的生产线或是激励供应商加班加点)或减小供应产能的方差(如加强对生产设备的预防性维护、加强对工人的培训教育以减少操作失误等)可以使装配商获益，且应依大均值、小方差与小差异三个指标进行供应商改进，即不单要提高零部件供应商的产能，还要使其更加稳定，并且要使各个零部件产能尽量匹配。另外，当各供应商供应能力相同时，改进成本较低的供应商对装配商而言更有利。这些模型结论与数值分析结果能为装配商的订购-定价决策以及供应商改进提供有益的借鉴。

本文是在信息对称的情况下展开研究，将来可考虑供需信息不对称下的信息甄别以及采购契约菜单的设计。