改进的萤火虫算法优化BP神经网络及应用

齐长兴，毕义明，李勇，范阳涛

(火箭军工程大学，陕西 西安 710025)

0 引言

弹道导弹突防作战效能评估是当前研究的一个重要方向，导弹突防效能评估研究已经取得了较大的进展[1]。文献[2]提出以拦截导弹对进攻弹的毁伤效果转化为进攻导弹突防效能的新思路。文献[3]运用大系统理论的分解协调法，采用关联预测法求解各子系统最优值。文献[4-7]借鉴运用数学建模方法，实现导弹突防效能的定量计算。上述这些研究方法，其原理可以归纳为仿真实验方法或者建立在线性模型的基础上。

随着智能算法理论的发展，BP(back propagation)神经网络(BPNN)理论在效能评估领域得到了创新发展和应用。文献[8-10]基于BP神经网络理论，分别建立了神经网络效能评估模型，验证了神经网络效能评估模型的可行性。但是，随着实践应用的深入，学者发现由于BP神经网络存在学习收敛速度缓慢，容易陷入局部最优解的问题，并采用智能算法对BP神经网络进行改进，取得了一些成果。文献[11]用遗传算法对BP神经网络权值和阈值进行优化，构建效能评估模型。文献[12]利用粒子群算法改进BP神经网络，但是粒子群算法收敛速度比较慢，鲁棒性不高。文献[13]采用了一种改进型的人工鱼群算法——基于自适应动态领域结构的人工鱼群算法，来优化BP神经网络，但是求解过程复杂，收敛性比较慢。本文提出了一种基于自适应动态领域结构的萤火虫算法，进行BP神经网络优化，建立神经网络效能评估模型，并对弹道导弹突防效能进行评估。

1 BP神经网络算法

BP神经网络构建在多层前馈网络的基础上，由输入层、隐含层和输出层组成，BP神经网络结构如图1所示[14]。通常情况下，输入层节点的个数取输入向量的维数，输出层节点的个数取输出向量的维数。目前，对于隐含层的个数没有明确的标准，需要根据研究的问题进行判定，根据已有的研究，选取单隐含层的BP神经网络结构，如图1所示。

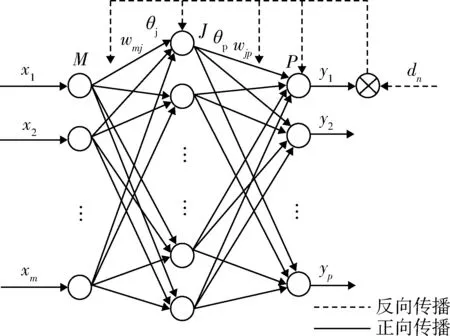
图1 BP神经网络基本结构Fig.1 Basic structure of BPNN

图1中，输入层有M个神经元，其输入矢量为x∈Rm，x=(x1,x2,…,xm)T；隐含层有J个神经元，其输出矢量为v∈Rj，v=(v1,v2,…,vj)T；输出层有P个神经元，其输出矢量为y∈Rp，y=(y1,y2,…,yp)T，期望输出矢量为d∈Rp，d=(d1,d2,…,dp)T。输入层到隐含层的权重值为wmj，阈值为θj；隐含层到输出层的权重值为wjp，阈值为θp；训练样本总误差为Ep。其中变量之间关系如下：

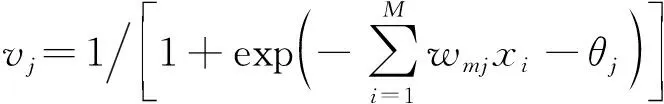
(1)

(2)

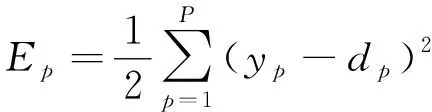
(3)

2 自适应步长萤火虫算法-BP神经网络算法

2.1 自适应步长萤火虫算法

2.1.1 基本萤火虫算法(FA)

萤火虫算法仿生原理是：将解空间的自由点模拟为自然界中的萤火虫个体，把搜索求解过程转化为萤火虫个体位置更新和移动过程，目标函数计算数值用萤火虫个体所处位置的优劣代替，萤火虫个体位置更新比为求解过程中最优解的迭代过程[15]。

(1) 荧光素更新

li(t+1)=(1-ρ)li(t)+γJi(t+1)，

(4)

式中：li(t)为萤火虫i在t时刻荧光素的数值；ρ(0<ρ<1)为荧光素的挥发速度，表示以往经验权重值；γ为荧光素增强系数，表示更新过程中的经验权重数值；Ji(t+1)表示萤火虫个体i在t+1时刻位置的目标函数值。

(2) 位置更新

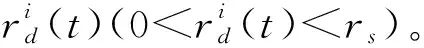
(5)

萤火虫个体i的邻域集合为

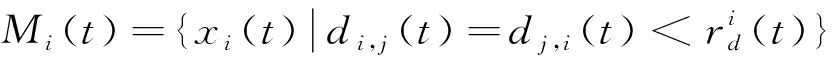
(6)

式中:Mi(t)为萤火虫i在t时刻的同伴集合。

(7)

式中:萤火虫i依据Pij选择出同伴j后，依据式(8)进行移动：

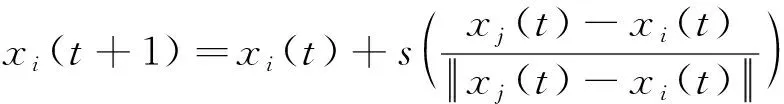
(8)

(3) 感知范围更新

β(nt-Ni(t))}},

(9)

式中:β为控制感知范围大小的参数;nt为控制感知范围内同伴数量的参数。

2.1.2 自适应步长萤火虫算法(SASFA)

在基本萤火虫算法中，萤火虫个体移动步长选取不恰当，导致搜索到的最优解陷入局部最优或者精度不高。针对存在的问题，设计自适应步长萤火虫算法：萤火虫个体在移动过程中，移动步长的选择与其感知决策域内的萤火虫个体分布密度有关。搜索步长取值大小与感知决策域内萤火虫个体分布密度成反比关系。

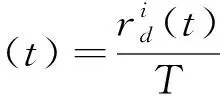
(10)

定义2平均邻域集合Ni(k,t)：在感知决策平均域α(t)内，萤火虫个体i在t时刻的同伴集合。

Ni(k,t)= {xi(t)di,j(t)=dj,i(t)<

α(t)+ε·rand()},

(11)

式中:k为第k个平均感知决策域，k=1,2,…,T；ε为扰动因子，ε∈[a,b]。引入ε·rand()随机数，主要考虑增强算法的精度，避免搜索结果陷入局部最优解。

定义3分布密度ηi(k,t)：指t时刻在第k个平均感知决策域内萤火虫个体i的同伴集合，与萤火虫i的在t时刻的同伴集合之间的比值。

(12)

那么，萤火虫算法的自适应移动步长描述为

si(k,t)=si(0,0)+φtηi(k,t)

,

(13)

式中:si(0,0)为初始化步长数值。

综上所述，萤火虫算法描述如下：

Step 1 初始化

设置l0,ρ,β,γ,rs,Nmax等参数初始值；将萤火虫随机部署在解空间，则种群中每只萤火虫在解空间中所处的位置可以描述为

xi=(xi1,xi2,…,xiD),i=1,2,…,m.

Step 2 荧光素更新

计算出萤火虫个体在t+1时刻的荧光素数值。

Step 3 位置更新

(1) 计算出每个萤火虫个体xi(t)的邻居集合Mi(t)；

(2) 计算集合中每个邻居的选择概率Pij，依概率选择出邻居j；

(3) 计算出移动步长s；

(4) 进行萤火虫位置移动更新。

Step 4 感知范围更新

Step 5 条件判断

当t>T，则转至Step 6；否则，转至Step 2。

Step 6 算法结束，输出结果

2.2 自适应步长萤火虫算法优化BP神经网络

2.2.1 基本原理

自适应步长萤火虫算法优化BP神经网络核心思想为：采用萤火虫种群的迭代优化来代替BP算法输出误差的梯度修正。将BP神经网络中的连接权值和阈值转化为萤火虫个体的位置向量，通过萤火虫算法在不同维度上的搜索变化过程，使得网络误差最小，满足输出要求或者达到最大训练次数。

2.2.2 算法设计

(1) 萤火虫位置向量设计

以图1为例，BP神经网络包含输入层、隐含层和输出层，每层包含的神经元个数分别为M,J,P，网络中阈值和权值分别为wmj,wjp和θj,θp。萤火虫个体位置向量结构如图2所示。

图2 萤火虫个体位置向量结构Fig.2 Individual position vector structure of firefly

BP神经网络需要优化的参数个数为

MJ+J+JP+P.

萤火虫个体位置向量表示为

x(t)= (x1,x2,…,xMJ,…,xMJ+J+JP+P)=

(w11,…,wMJ,θ1,…,θJ,w11,…,

wJP,θ1,…,θP).

(14)

(2) 算法描述

基于自适应步长萤火虫算法优化BP神经网络的步骤如下：

Step 1 初始化BP神经网络

设计BP神经网络拓扑结构，设置输入层、隐含层和输出层的权值(w)、阈值(θ)、训练次数和训练误差。

Step 2 初始化萤火虫算法

设置l0,ρ,β,γ,rs,T等参数初始值；种群中每只萤火虫在解空间中所处的位置向量为

x(t)= (w11,…,wMJ,θ1,…,θJ,

w11,…,wJP,θ1,…,θP).

Step 2 荧光素更新

计算出萤火虫个体在t+1时刻的荧光素数值，并将式(3)作为目标函数。

Step 3 位置更新

(1) 计算出每个萤火虫个体xi(t)邻居集合Mi(t)；

(2) 计算集合中每个邻居的选择概率Pij，依概率选择出邻居j；

(3) 计算出移动步长s；

(4) 进行萤火虫位置移动更新。

Step 4 感知范围更新

Step 5 条件判断

当t>T，则转至Step 6；否则，转至Step 2。

Step 6 确定权值(w)、阈值(θ)

将萤火虫最优位置向量映射给BP神经网络，作为BP神经网络的初始权值和阈值。

Step 7 BP神经网络训练

使用训练样本对神经网络进行训练，直至达到满足条件，并记录此时网络状态；否则，继续训练。

3 基于SASFA-BP神经网络的弹道导弹突防效能评估模型

3.1 弹道导弹突防效能评估指标体系

弹道导弹突防效能评估指标体系涉及到因素比较多，复杂度较高，在以往研究成果基础上，构建弹道导弹突防效能评估指标体系，如表1所示。

表1 弹道导弹突防效能评估指标体系

3.2 弹道导弹突防效能评估模型

(1) BP神经网络结构设计

1) 输入层节点数设计

因素层指标共16个，则BP神经网络的输入层节点数为16。

2) 输出层节点数设计

以弹道导弹突防效能作为输出值，因此输出层节点数为1。

3) 隐含层节点数设计

目前，通常使用经验公式计算和试凑法相结合办法，来确定隐含层节点数。

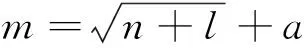
(15)

式中:n为输入层节点数;l为输出层节点数;m为隐含层节点数;取a=7，则隐含层节点数为11。

(2) 构建基于SASFA-BP神经网络的评估模型

根据设计的BP神经网络结构，构建基于SASFA-BP神经网络的效能评估模型，以因素层指标作为神经网络的输入值，目标层指标作为神经网络的输出值。

(3) 评判等级集合的确定

借鉴经验做法，可将导弹突防效能评估值划分为5个等级：低、较低、一般、较好、好，分别用Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ来表示，这样得到评价等级集合：U={Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ}。

评判等级与导弹突防效能评估值的对应关系如下表2所示，表中所列数值实际是评判等级的量化指标或者分级标准。

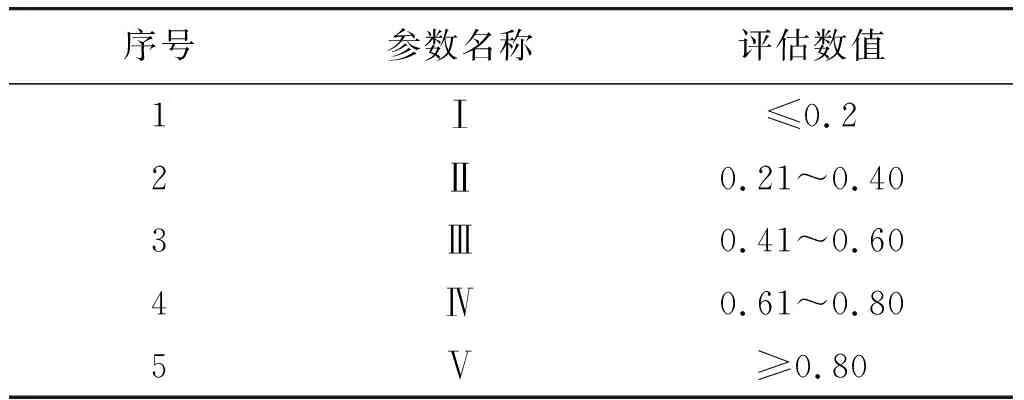
表2 评判等级的量化指标

4 算例分析

以某型号弹道导弹为例，针对某导弹防御系统进行导弹突防效能评估试验，经过多次试验获得试验数据，作为训练样本数据，并以其中的3组作为测试数据。

用文中提出的自适应萤火虫算法优化的BP神经网络进行导弹突防效能值预测，并用Matlab2014a编写算法程序。算法相关参数设置如表3所示。

采用训练后的BP神经网络模型进行预测，预测结果如表4所示。

从表4中可以看出，经过训练后的网络可以达到最优状态，误差率接近0，说明神经网络模型评估值为有效评估值，评估结果可靠、可信。

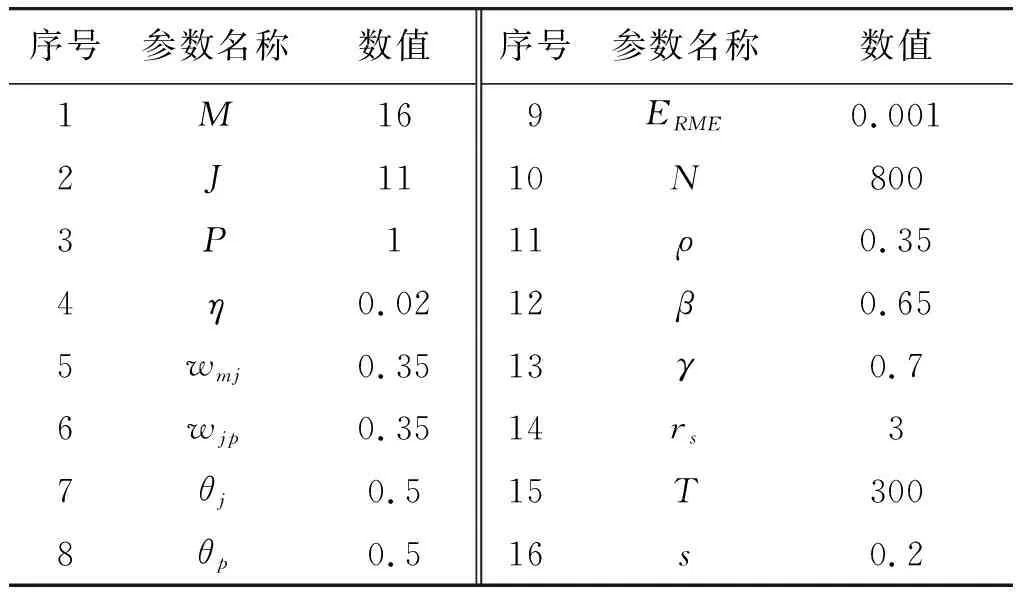
表3 初始参数设置表

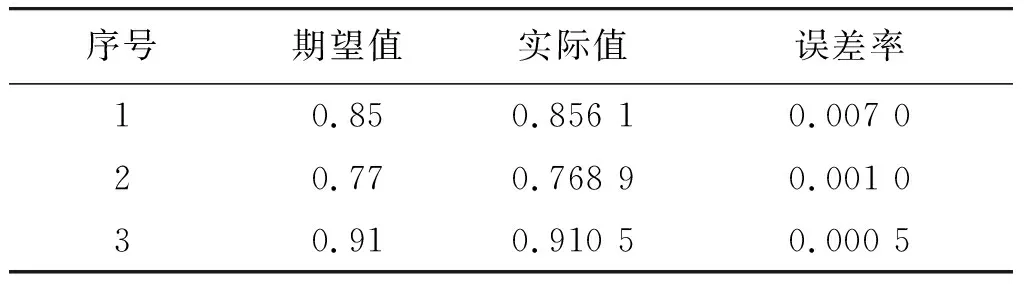
表4 测试结果

4.1 仿真分析

在同等条件下，设定BP神经网络训练误差ERME分别为0.01,0.001,0.000 5，运用Matlab2014a软件分别对BPNN,FA-BPNN和SASFA-BPNN训练，神经网络训练误差曲线分别如图3～5所示。

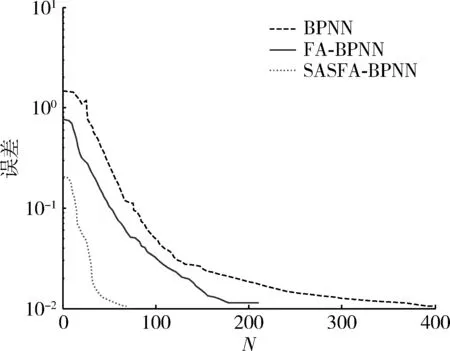
图3 ERME=0.01条件下误差曲线图Fig.3 Error curve while ERME=0.01

在同等条件下，将测试数据分别运用BPNN,FA-BPNN和SASFA-BPNN进行运算，计算结果如表5所示。

图4 ERME=0.001条件下误差曲线图Fig.4 Error curve while ERME=0.001

图5 ERME=0.000 5条件下误差曲线图Fig.5 Error curve while ERME=0.000 5

期望值实际值相对误差(%)SASFAFABPSASFAFABP0.850.850 60.863 20.885 60.0711.5614.1980.770.769 90.786 30.746 60.0112.1223.0270.910.910 50.908 90.876 30.0562.3683.701

4.2 结果分析

(1) 从图3～5中可以得出，在相同的误差要求下，SASFA-BPNN的训练次数少。例如，图3中，FA-BPNN，BPNN的训练次数是SAFA-BPNN训练次数的1.78倍和2.1倍；图4中，FA-BPNN,BPNN的训练次数是SASFA-BPNN训练次数的2.2倍和3.1倍；图5中，FA-BPNN,BPNN的训练次数是SAFA-BPNN训练次数的3.5倍和4.3倍。通过对比分析可以得出，当ERME取值较大值时(ERME=0.01)，在网络训练之后都能够达到目标误差；但是当ERME取较小值时(ERME=0.001,0.000 5)，SAFASO-BPNN,FA-BPNN在网络中训练之后都能够达到目标误差，而BPNN在网络中训练之后不能够达到目标误差。

(2) 分析表4中的数据可以得出，3种算法输出结果的相对误差最大值之比为：1∶33∶61；3种算法输出结果的相对误差最小值之比为：1∶143∶277。这些数据反映了SASFA-BPNN算法精度明显优于FA-BPNN，BPNN。

(3) 综上分析，SASFA-BPNN在实践应用中，计算精度高、收敛速度快，可以有效解决效能评估领域问题。

5 结束语

本文从萤火虫仿生智能算法入手，有针对性的提出自适应步长改进思路，克服了传统萤火虫算法收敛速度慢和易陷入局部最优解的缺陷。并将改进后的萤火虫算法与BP神经网络结合，提出了基于自适应步长萤火虫算法优化BP神经网络的效能评估模型。通过仿真计算，证明了自适应步长萤火虫算法的优越和评估模型的合理可靠。同时，也为效能评估提供一种可信、可用的评估方法，具有一定的借鉴意义。但是，在实际应用过程，由于研究对象涉及到的因素比较多，如何合理、科学的设计神经网络的结构以及各层包含的神经元个数，为今后研究提供一个重要方向和内容。