临近空间高超声速目标跟踪IMMCPF算法

赵凯丽，高火涛，曹婷

(武汉大学 电子信息学院，湖北 武汉 430072)

0 引言

临近空间一般泛指距离海平面高度20～100 km的高空区域，临近空间高超声速飞行器因其机动特性强、轨迹变化快、强非线性等特点[1-2]，使这类飞行器很难被雷达跟踪，有很好的隐身性，极难防御，如近几年出现的X-51A[3]高超声速飞行器， 对空天安全造成了巨大威胁。因此，临近空间高超声速目标跟踪相关算法的研究对空天安全的保障、促进空天防御技术发展都具有重大意义。

临近空间目标跟踪对于普通机动目标跟踪中使用的单一模型跟踪效果较差，难以覆盖其可能采取的机动形式，而文献[4-5]则证明多种目标模型相互之间交互耦合使用的交互式多模型(interacting multiple model, IMM)算法对临近空间目标跟踪有更好的效果。经典IMM算法中使用的是Kalman滤波来对目标状态做滤波预测，但是在临近空间中，环境恶劣，飞行轨迹受到各种扰动和空气阻力的影响，这使得状态方程和量测方程具有很高的非线性，而Kalman滤波算法仅对线性方程有较好的滤波效果，非线性方程滤波误差会增加。

针对临近空间的这一特点，国内外已有学者相继提出了一些基于IMM算法的改进算法，如秦雷使用扩展卡尔曼滤波(extend Kalman filter,EKF)[6]、Julier S使用无迹卡尔曼滤波(unscented Kalman filter,UKF)[7]、曹亚杰使用粒子滤波[8](particle filter,PF)分别来代替经典IMM算法中的Kalman滤波来对目标状态进行估计。虽然这些改进算法都在一定程度上对目标跟踪精度有所提高，但是EKF算法仅在非线性较弱时效果较好，当系统为强非线性环境时，状态的估计精度和稳定性都会有所影响，使目标跟踪误差较大[9]。UKF算法虽然滤波精度高于EKF算法，但是它必须设置比例因子等相关参数的值，而这些参数值的选取目前并没有确切的理论依据，并且这些参数的选择对滤波的效果影响极大。PF算法的滤波精度要高于EKF或者UKF，在非线性系统中属于滤波效果较好的算法，但是标准的PF算法在滤波过程中并没有融入当前时刻的量测信息，进而导致滤波精度下降甚至出现滤波发散现象，而引入了容积卡尔曼滤波的容积粒子滤波算法( cubature particle filter,CPF)，因加入了当前时刻的观测信息，使其重要性密度函数与后验概率函数更加接近，从而使算法的滤波性能进一步提升[10-11]，目标跟踪效果更好。

本文将CPF算法与IMM算法相结合，形成交互式多模型容积粒子滤波算法(interacting multiple model cubature particle filter,IMMCPF)。IMMCPF算法使用IMM算法对目标进行跟踪，并使用CPF算法做IMM算法中的滤波预测，得到目标状态的估计值，即使用容积数值积分原则来计算非线性随机变量的均值和协方差，这种方法既避免了求导运算，同时也加入了当前时刻的观测信息，使其重要性密度函数与其后验概率函数更加接近，从而使算法的滤波性能得到提升。从上面的分析中可看出，IMMCPF算法能很好的实现对临近空间高超声速目标的高精度跟踪，仿真实验也验证了本文算法的可行性。

1 临近空间高超声速目标飞行轨迹研究

根据美国公开的X-51A飞行器的部分数据[12]分析可知，高超声速飞行器的飞行过程大致如下：飞行器和助推器由轰炸机搭载，携带至约16 km的高空，并脱离飞行器，与此同时助推级开始点火，把飞行器推行到19 km的高空，飞行Ma约为4.5；然后助推级与飞行器脱离，飞行器在无动力情况下滑行，此时，超燃冲压发动机开始点火，飞行Ma达到5，进入距离地面20 km的临近空间，关闭发动机，进入无动力滑翔阶段；最后发动机重新提供动力，将飞行器推送到新的高度。重复上述过程，一直到达预定的目的地上空，进入俯冲攻击阶段，攻击目标，完成作战任务。

根据临近空间高超声速飞行器的飞行轨迹特点，本文近似拟合出了飞行器的整个运动过程大致如下图1所示。图2和图3分别为飞行器的速度和加速度曲线。

图1 飞行器轨迹Fig.1 Aircraft trajectory

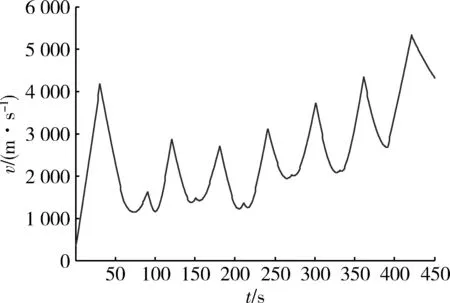
图2 飞行器速度变化曲线Fig.2 Velocity curve of the aircraft

图3 飞行器加速度变化曲线Fig.3 Acceleration curve of the aircraft

从图1的轨迹曲线看，飞行器飞行在上万米的高空中，其轨迹变化复杂，且有很强的非线性，难以跟踪；从图2的速度变化曲线看，飞行器的平均飞行Ma能达到5～6，飞行速度极快；而从图3中能看出，临近空间高超声速目标的机动特性非常强。所以传统的目标跟踪方法在临近空间中跟踪误差较大，需要研究新的算法来对临近空间高超声速目标进行跟踪。

2 交互式多模型算法

根据上述仿真得到的临近空间高超声速目标的飞行轨迹曲线，本文选择使用对复杂的机动目标跟踪有较好效果的IMM算法来跟踪临近空间高超声速目标[13]。它采用多个单一模型来共同描述目标的运动状态，然后通过对不同模型分配相应的权值来反映目标运动状态，最后对各模型加权融合即为所估计结果，因此该算法能很好的跟踪临近空间高超声速目标。

交互式多模型算法[14-15]是1988年Blom和Bar-Shalom在广义伪贝叶斯算法的基础上进一步提出的，该算法中有一个包括目标整个运动状态的模型集M，其中的任意一个模型都有一个对应的滤波器与之相匹配，每个模型之间又可相互转换，模型之间两两对应的相互转换与马尔可夫过程一致，每个模型对应的滤波器都并行运行，算法最终的结果是各个模型跟踪结果的加权平均值[16-17]。

IMM算法的一个循环大致可分为4个部分：输入交互、滤波预测、模型概率更新、数据融合[18]。

假定在IMM算法中一共有m个模型集，各模型集对应的离散状态方程可表示为

X(k+1)=FjX(k)+ωj(k)，j=1,2,…,m，

(1)

式中：Fj为模型j的状态转移矩阵；ωj(k)是均值为0，协方差为Qj的过程噪声。

模型j的量测方程为

Z(k)=HjX(k)+vj(k)，

(2)

式中：Hj为模型j的观测矩阵；vj(k)为观测噪声，其协方差值为R。

系统的马尔可夫转移矩阵为

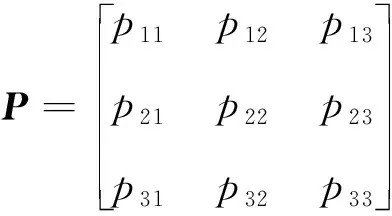
(3)

式中：pij为从模型i到模型j的转移概率。

(1) 输入交互

μij(k-1k-1),

(4)

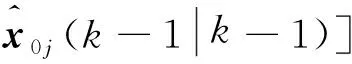
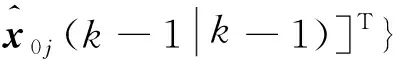
(5)

式中：

(6)

(7)

(2) 滤波预测

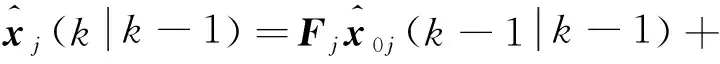
(8)

(9)

(10)

Sj(k)=HjPj(kk-1)HT+R，

(11)

(12)

(13)

(14)

(3) 模型概率更新

通常模型概率更新都会选择使用最大似然函数法，根据该方法得到的似然函数值来计算各个模型与当前时刻目标运动模式的匹配值。

k时刻时，与第j个模型相匹配的最大似然函数可由式(15)计算得出：

(15)

则模型j的后验概率为

(16)

式中：c为归一化常数，

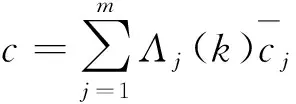
(17)

(4) 数据融合

在计算出各个模型的输出概率和相应的输出结果后即可求得k时刻的交互式最终输出结果：

(18)

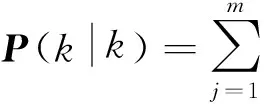
(19)

以上即为IMM算法的一次完整的循环过程，当进行下一时刻的交互循环时，就可把上面求得的输出结果当作下一时刻交互输入的输入值代入运算，计算新一轮的交互输出。

3 IMMCPF算法

由于临近空间高超声速目标的飞行轨迹具有很强的非线性特性，而交互式多模型算法的滤波预测中使用的是卡尔曼滤波，卡尔曼滤波对强非线性目标的跟踪效果不理想，有时甚至可能会出现滤波发散的现象。针对这个问题，本文选择使用容积粒子滤波算法来代替Kalman滤波完成IMM算法的滤波预测过程，即提出一种新的IMMCPF算法来跟踪临近空间高超声速目标。

IMMCPF算法将IMM算法和CPF算法相结合，它使用一组权值大小一样的容积点集来代替贝叶斯估计中复杂的积分运算，降低了算法复杂度，并且该算法在产生PF的重要性密度函数时进一步加入了当前时刻最新观测值，从而使其生成的重要性密度函数与系统真实的后验概率密度函数更加接近。因此，IMMCPF算法在非线性系统中有更好的滤波性能，对临近空间高超声速目标的跟踪也有很好的效果。

(20)

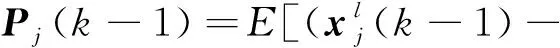
(21)

时间更新：

(22)

(23)

(24)

(25)

量测更新：

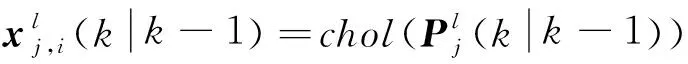
(26)

(27)

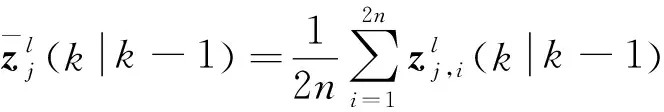
(28)

(29)

(30)

(31)

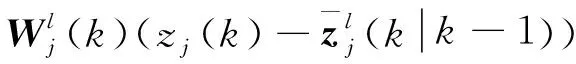
(32)

(33)

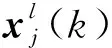
更新粒子权值并归一化：

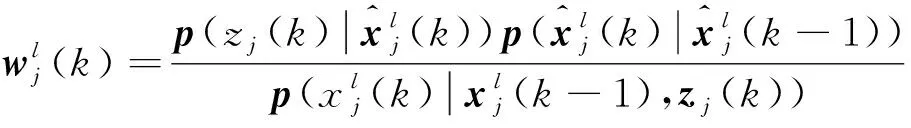
(34)

(35)

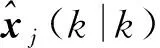
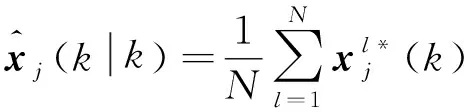
(36)

(37)

4 仿真结果与分析

本文拟根据X-51的试飞轨迹来建立临近空间目标仿真模型，并利用本文算法对临近空间高超声速目标进行跟踪，验证所提算法性能。

根据临近空间高超声速目标的飞行轨迹特征，本文选择的交互式多模型算法中包含3个经典的模型，2个Singer模型和1个Current模型。

(1) Singer模型：对一般的机动目标(目标机动不大时)有较好的跟踪效果。

模型的状态方程：

X(k+1)=FX(k)+ω(k)

，

(38)

式中：F为状态转移矩阵，

(39)

ω(k)为过程噪声，协方差为

(40)

式中：

q11= 1/2α5(1-e-2αT+2αT+2α3T3/3-

2α2T2-4αTe-αT),

q12= 1/2α4(e-2αT+1-2e-αT+

2αTe-αT-2αT+α2T2),

q13=1/2α3(1-e-2αT-2αTe-αT),

q22=1/2α3(4e-αT-3-e-2αT+2αT),

q23=1/2α2(e-2αT+1-2e-αT),

q33=1/2α(1-e-2αT),

(41)

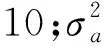
(2) Current模型：Current模型能自适应地调节加速度范围，对加速度变化较大的目标有更好的跟踪效果。

模型的状态方程：

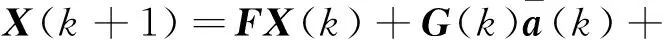
(42)

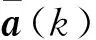
G(k)=

(43)

式中：T与α的定义与Singer模型相同。

本文仿真使用的3个模型的初始概率为(1/3,1/3,1/3)，3个模型之间的马尔可夫转移矩阵为

(44)

(45)

目标位置的均方根误差定义为

(46)

利用IMMEKF算法、IMMPF算法、IMMCPF算法仿真得到的目标跟踪轨迹与目标真实运动轨迹对比图如图4所示。图5是粒子数为100时各滤波算法在各方向上经历100次MC仿真后的目标位置均方根误差图，图6是相对应的目标速度均方根误差图。

图4 各算法滤波结果对比图Fig.4 Filter results comparison of eaeh algorithm

图5 位置RMSEFig.5 Position RMSE

从图5,6中可以看出，无论x方向位置RMSE、y方向位置RMSE，还是x方向速度RMSE、y方向速度RMSE，IMMEKF算法的估计精度都是最低的，IMMPF算法稍微高些，IMMCPF算法跟踪得到的估计精度最高。这是因为临近空间高超声速目标的飞行轨迹具有很强的非线性，而IMMEKF算法仅在非线性较弱时效果较好；IMMPF算法对强非线性有较好的效果，但是容易产生粒子退化问题导致滤波精度下降，而IMMCPF算法的重要性密度函数中因加入了当前时刻最新的观测信息来产生预测粒子集，这样其生成的重要性密度函数与其最优的重要性密度函数更加接近，所以IMMCPF算法的跟踪结果精度最高。

表1为3种算法经历100次MC仿真后各状态量的RMSE对比，从表1的数据中可以清楚的看出本文所使用算法对目标跟踪精度的提升。相比于IMMEKF算法，IMMCPF算法位置RMSE提升了13.12%，速度RMSE提升了28.21%；相比于IMMPF算法，IMMCPF算法位置RMSE提升了8.32%，速度RMSE提升了8.51%。

图6 速度RMSEFig.6 Velocity RMSE

RMSE算法IMMEKFIMMPFIMMCPF位置RMSE/mx方向103.251 197.839 389.697 2y方向119.158 398.352 389.633 6速度RMSE/(m·s-1)x方向99.140 377.788 471.167 4y方向122.245 480.849 576.496 2

由此可以看出，本文提出的IMMCPF算法与IMMEKF算法和IMMPF算法相比具有更高的精度和更好的鲁棒性，对临近空间高超声速目标的跟踪也有更好的效果。

5 结束语

本文根据临近空间高超声速目标的飞行轨迹特性，选择使用IMM算法来跟踪这类目标，但是经典IMM算法中使用的卡尔曼滤波在非线性系统中滤波精度不高，针对这个问题，本文选择使用CPF算法来代替IMM算法中的Kalman滤波算法，从而形成了一个新的IMMCPF算法。该算法使用CPF算法对目标进行滤波预测，它融入了当前时刻的观测信息，使其重要性密度函数更加逼近后验概率函数，从而使其滤波精度提高，对临近空间高超声速目标的跟踪有更好的效果。仿真结果也表明，IMMCPF算法各状态量的估计精度均优于IMMEKF算法、IMMPF算法。由此可看出，IMMCPF算法在临近空间高超声速目标跟踪中有更好的跟踪效果，说明该算法有一定的实用价值。