浮空式角反射体质心干扰使用时机研究
王聘,胡生亮,张俊
(海军工程大学 兵器工程学院,湖北 武汉 430033)
0 引言
随着反舰导弹的攻击速度越来越快,水面舰艇的近程防御手段可有效干扰的时间越来越短,而且受到发射装置不能自动补弹等因素的制约,舰载无源干扰资源有限。因此,如何在有限的干扰时间和作战资源内提高无源干扰效率,正确的干扰弹投放时机是一项重要影响因素。
无源干扰器材主要分为箔条和角反射体2种,但箔条云和舰船雷达回波在极化特性、散射点分布等方面存在一定的差异,且目前部分采用逻辑处理电路的新型反舰导弹利用时间、空间或极化特性已经可以有效识别箔条[1-3],这对单一箔条的作战能力提出了严峻的挑战。与箔条相比,角反射体阵列在散射、频宽、极化及抗相参性等方面都具有自身优势,其在时域、频域和空域上与雷达回波都没有显著差异,在理论上可以对多种体制、各个方向的雷达进行干扰[4-5]。
浮空式角反射体是近十几年才发展起来的一种新型无源干扰器材,角反射体装填在运载器(如通用箔条弹弹舱)中,利用通用无源发射装置发射并飞至距载舰一定位置后,从运载器中脱离并展开成形,对来袭反舰导弹实施无源干扰。目前,以美国为代表的西方国家海军的水面舰艇开始运用并装备该型角反射体[6],而国内关于浮空式角反射体的基础理论研究特别是作战使用研究方面基本处于空白。未来对海远程精确打击时,作战对手使用浮空式角反射体干扰弹实施末端干扰的可能性极大,这对战时反舰导弹的突防构成重大威胁。为提升反舰导弹对该型角反射体的突防能力,需尽快开展浮空式角反射体的电磁散射特性及作战使用等研究。
考虑到篇幅限制,本文仅对浮空式角反射体的质心干扰使用时机展开研究。借用箔条的作战经验[7],以有效干扰距离作为判断干扰时机的依据,提出适用于浮空式角反射体质心干扰的有效干扰距离确定方法,然后以“亚声速”和“超声速”2类典型反舰导弹为干扰对象,以浮空式角反射体阵列为假目标进行质心干扰模拟对抗,将理论分析与仿真验证相结合,给出某典型作战环境下浮空式角反射体干扰弹的具体投放时机,从而为其未来实际作战使用提供依据,也为反舰导弹对抗浮空式角反射体干扰提供理论参考。
1 浮空式角反射体概述
浮空式角反射体作为一种新型无源干扰器材,具有布放时间短、布放效率和精度较高的特点,且在空中有一定的滞空时间,便于与箔条等其他无源干扰器材配合使用,在对抗具备箔条识别能力的反舰导弹方面具有明显优势,是角反射体的重要发展方向之一。
目前,浮空式角反射体干扰弹作为一类重要的舷外无源干扰器材已经列装于以法国、德国为代表的北约国家及其他盟国海军水面舰艇。其典型代表有以色列“维扎德(Wizard)”反雷达假目标[8]、丹麦“PW216 Mod2”箔条/角反射体复合干扰弹[9]、法国“希尔蒙(Sealem)”角反射体诱饵[10]以及德国“舷外角反射体(OCR)” 诱饵[11]。其中,以色列“维扎德(Wizard)”反雷达假目标在2005年末首次海上试验便取得圆满成功,该假目标的特点是采用气囊悬浮的方式实现在空中的飘浮。德国“舷外角反射器(OCR)”载荷于2014年在德国海军K130级轻型护卫舰Magdeburg完成测试,并于2015年底完成鉴定,该诱饵的特征是应用降落伞,使下降的速度减慢,可以实现超过1 min的飞行状态。“维扎德(Wizard)”和“舷外角反射器(OCR)”的展开效果如图1所示。

图1 “维扎德”和“舷外角反射器”展开效果图Fig.1 Unfold effect of the “Wizard” and “OCR”
借鉴外军研究经验,国内浮空式角反射体以某型干扰弹作为运载器,在结构上采用框架式、伞降式结构。以刚性支撑杆为主要支撑部件,金属反射面通过高强度金属丝与支撑框架缝合,其最大的优点在于可以很好的保持反射面的平整度与面间垂直度。角反射体未展开时,支撑杆在外力作用下处于收缩折叠状态,作为载荷装填入弹舱;当角反射体在空中被抛射出舱后,利用气动伸缩装置使其迅速恢复伸展状态,并在吊伞的作用下实现浮空。依据运载器空间推算出该浮空式角反射体主要技术参数如表1所示。

表1 浮空式角反射体主要技术参数
2 质心干扰成功基本条件
质心干扰是箔条干扰中的一种典型样式,其理论研究已经非常充分[12-13],本文不再详细描述。从作战效果角度来说,角反射体同为无源干扰器材,也可以达到质心干扰的效果,因此,本文借用箔条质心干扰基本理论对浮空式角反射体的质心干扰进行研究。其中,导弹、舰艇、浮空式角反射体阵列的质心干扰态势图如图2所示。

图2 质心干扰态势图Fig.2 Situation of centroid jamming
图中,目标舰与浮空式角反射体阵列组成的假目标均在末制导雷达跟踪波束内,目标舰雷达截面积为δ1,假目标雷达截面积为δ2。以导弹当前位置M点为基准,末制导雷达波束角宽度为θ,真假目标之间的夹角为θ1,导弹末制导雷达跟踪真假目标形成的质心点Z与目标舰的夹角为θ2。则
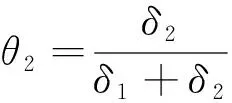
(1)
由式(1)可知,假目标雷达截面积越大,质心点与目标舰的夹角就越大,导弹末制导雷达的跟踪点就离目标舰越远。
若使质心干扰成功,需满足以下基本条件[14]:
(1) 假目标布放位置。为形成有效的质心效应,要求假目标必须布放在导弹末制导雷达距离和方位跟踪波门内,并尽量拉开与水面舰艇的距离。
(2) 假目标反射能量。由图2知,末制导雷达跟踪点取决于假目标与水面舰艇的雷达有效反射面积之比。因此,为达到较好的质心干扰效果,即质心点Z偏向假目标,要求浮空式角反射体阵列的雷达有效反射面积δ2应大于水面舰艇的雷达有效反射面积δ1。
(3) 假目标在空中要有足够的留空时间。假目标在末制导雷达跟踪波门内要有足够的留空时间,以满足导弹跟踪和控制的要求。
(4) 水面舰艇需进行合理的战术机动。合理的战术机动可以使水面舰艇在方位上能迅速拉开与假目标的距离,以提高质心干扰效果。
其中,条件(1),(2)在战术技术上均已得到解决,条件(4)需根据战场环境态势实时做出机动,该情况将在后续研究中作深入分析,本文不予考虑。条件(3)中由于浮空式角反射体采用吊伞技术使角反射体实现浮空,浮空时间有限,因此,开展有限浮空时间条件下如何在正确时机施放假目标的研究,是十分必要的。
3 质心干扰使用时机研究
现代雷达对目标探测时,可以直接获取目标的距离、速度和方位信息[15]。根据这一特点,以反舰导弹与舰艇的距离作为判断质心干扰时机的依据,并针对不同作战环境做出有效干扰距离分析。
3.1 有效干扰距离分析
(1) 最小干扰距离
为使质心干扰有效,假目标在形成有效干扰时应处于末制导雷达分辨单元内,才能有效干扰雷达制导系统。以干扰形成时舰艇和假目标正好处于末制导雷达波束角的边界为临界情况,考虑舰艇逆风行驶,假目标随风移动,且舰艇和假目标的行进路线与导弹攻击方向垂直。并作如下假设:
设舰艇在T时刻发现导弹且与舰艇的距离为RM,导弹速度为vM,末制导雷达波束角为θ,系统反应时间为ΔT(包括系统决策时间、武器系统反应时间),干扰弹发射到形成有效干扰时间为TF,假目标的发射距离为R0,舰艇航行速度为vS,战场风速为vW,则根据质心干扰原理可得
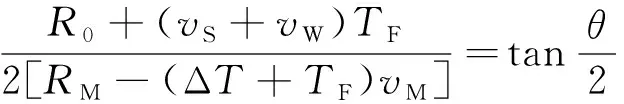
(2)
即
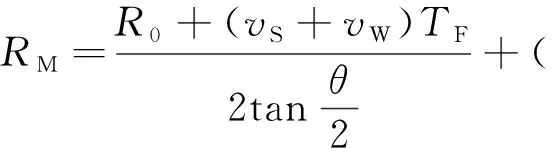
(3)
在该种情况下,舰艇实施质心干扰的有效时间为0,因此定义此时舰艇与导弹的距离为最小干扰距离,即

(4)
式(4)表明,若导弹离舰艇的距离大于Rmin时实施质心干扰,则干扰有效,否则舰艇和角反射体阵列假目标不能同时处于末制导雷达波束角范围内,质心干扰无效。
(2) 最大干扰距离
理论上,当舰艇目标接收到反舰导弹末制导雷达开机或跟踪信号时应立即实施无源质心干扰。但考虑到目前远距离反舰导弹其末制导距离一般在25 km以上且浮空式角反射体滞空时间有限,存在导弹尚未逼近舰艇,假目标便已经失效的情况。因此,本文具体从以下2方面讨论最大干扰距离。
1) 当反舰导弹末制导雷达开机距离大于假目标滞空时间内的最大有效干扰距离时,应以假目标的滞空时间作为判断最大干扰距离的依据。设假目标滞空时间为TZ,其他参数同上,则

(5)
(ΔT+TF+TZ)vM.
(6)
在该种情况下,舰艇实施质心干扰的有效时间为TZ,为保证反舰导弹末制导雷达开机时假目标始终滞留于空中,要求舰艇对导弹的干扰距离不能大于RM,定义此时RM为最大干扰距离,即
(ΔT+TF+TZ)vM.
(7)
2) 当反舰导弹末制导雷达开机距离小于假目标滞空时间内的最大有效干扰距离时,应以反舰导弹末制导雷达开机信号作为判断最大干扰距离的依据。设末制导雷达开机距离为RK,其他参数保持不变,此时需满足假目标形成时末制导雷达已开机的条件,质心干扰才能成功,则
RM-vM(ΔT+TF)≤Rk,
(8)
即
RM≤vM(ΔT+TF)+Rk.
(9)
将RM=vM(ΔT+TF)+RK定义为该种情况下质心干扰的最大有效干扰距离,即
Rmax2=vM(ΔT+TF)+Rk.
(10)
以上分析表明,在上述2种情况下,若在导弹距离舰艇的距离小于最大干扰距离时实施质心干扰,可对导弹进行有效干扰,否则干扰失效。
综上所述,最小干扰距离和最大干扰距离在理论上分别给出了质心干扰的最晚及最早的使用时机,即只有导弹与舰艇的距离介于最小干扰距离和最大干扰距离之间时,实施质心干扰才可能有效。
3.2 不同作战环境下质心干扰使用时机分析
以有效干扰距离为基础,结合不同作战背景条件,对质心干扰的使用时机进行具体分析:
(1) 来袭导弹距离信息明确时,质心干扰时机的确定
假设舰艇在T时刻发现导弹且与舰艇的距离为RM,根据RM与Rmin和Rmax1,Rmax2之间的关系来确定质心干扰的使用时机。
1) 当RM>Rmax1或RM>Rmax2时,此时应至少延迟ΔT1或ΔT2实施质心干扰,其中ΔT1=(RM-Rmax1)/vM,ΔT2=(RM-Rmax2)/vM。
2) 当Rmin 3) 当RM (2) 来袭导弹距离信息未明确时,质心干扰时机的确定 若无法获取T时刻舰艇与导弹的距离信息,可以末制导雷达开机信号为依据引导实施质心干扰。当舰艇接收到末制导雷达开机信号时,立即施放浮空式角反射体干扰弹进行干扰,若反舰导弹为超声速反舰导弹或开机距离较近时,单次施放即可达成有效干扰;若侦测到反舰导弹为亚声速或开机距离较远时,在实施干扰一段时间后再补发相应的干扰弹。 由第3节可知,质心干扰时机由有效干扰距离决定,而确定有效干扰距离前首先要判断假目标滞空时间内最大干扰距离与末制导雷达开机距离的大小关系,若假目标的最大干扰距离小于反舰导弹末制导雷达的开机距离,则以假目标的滞空时间作为判断最大干扰距离的依据,否则以末制导雷达开机和跟踪信号为依据。 为验证上述理论,本文分别以某典型“亚声速”反舰导弹和“超声速”反舰导弹为干扰对象进行仿真。同时,为便于计算,本文假定浮空式角反射体的作用距离为150 m,有效浮空时间为50 s,具体分析如下: 以某典型亚音速反舰导弹为例,其飞行Ma数为0.75,末制导雷达开机距离为25~30 km,末制导雷达波束宽度为5°,风速为5 m/s,舰艇正常航速为15 kn(1 kn=0.514 m/s),全速航行航速为25 kn,且假定系统反应时间为3 s,角反射体干扰弹自发射至假目标成形用时5 s。 根据以上战场环境,利用本文提出的方法计算出浮空式角反射体滞空时间为50 s时不同作战条件下的最小干扰距离和最大干扰距离,结果如表2所示。 表2干扰亚声速反舰导弹有效距离 Table2Effectiveinterferencedistanceof 干扰亚声速反舰导弹Rk=25 km,vM=25 knRk=25 km,vM=15 knRk=30 km,vM=25 knRk=30 km,vM=15 kn最小干扰距离/km5.1784.8825.1784.882最大干扰距离/km26.26123.21726.26123.217 对比表2中数据可以发现,当导弹末制导雷达开机距离为25 km、舰艇航速为25 kn时,浮空式角反射体最大有效干扰距离为26.261 km,大于末制导雷达的开机距离,说明此时应以末制导雷达开机信号为依据判断最大干扰距离,且该种情况下质心干扰的有效时间要小于50 s。而对于另外3种情况,其最大有效干扰距离均小于末制导雷达的开机距离,此时应以假目标滞空时间为依据判断最大干扰距离,且其有效干扰时间均为50 s。 为验证上述分析的正确性,仿真舰艇脱离亚声速反舰导弹导引头3 dB波束水平视场所需的时间,仿真结果如图3所示。 图3中,反舰导弹视场表示某一时刻末制导雷达的半功率点波瓣宽度,即3 dB波束宽度;舰艇诱饵分离曲线表示随时间推进,舰艇诱饵拉开的距离;2条曲线的交汇点表示舰艇与诱饵的距离正好等于反舰导弹末制导雷达3dB波束宽度。反舰导弹视场从末制导雷达开机时刻(t=0)开始计时,随时间推进逐渐减小;同时,由于系统反应时间为3 s,角反射体干扰弹自发射至假目标成形用时5 s,因此,舰艇诱饵分离曲线从t=8 s开始,其随时间推进逐渐增大。 图3 舰艇摆脱亚声速反舰导弹跟踪最小时间统计Fig.3 Minimum time for warship getting rid of the subsonic anti-ship missile′s tracking 由图3可看出,当末制导雷达开机距离为25 km,舰艇航速为25 kn时,诱饵在末制导雷达开机后47 s时与舰艇分离为2个目标,不再满足质心干扰的条件,其有效干扰时间为47 s;若舰艇航速为15 kn,诱饵在末制导雷达开机后53 s时与舰艇分离为2个目标,不再满足质心干扰的条件。同理,当末制导雷达开机距离为30 km时,上述2种情况的分离时间变为57 s和64 s。对于后3种情况,虽然其舰艇诱饵分离时间大于50 s,但其有效干扰时间取决于假目标滞空时间,且均为50 s。可见,仿真结果与理论分析结果相吻合,验证了本文所提出的方法的正确性。 同理,以某典型超声速反舰导弹为例,其飞行Ma数为2.3,其他参数同上,获取浮空式角反射体滞空时间为50 s时不同作战条件下的最小干扰距离和最大干扰距离,计算结果如表3所示。 表3 干扰超声速反舰导弹有效距离 对比表3中数据可知,对于飞行Ma为2.3的超声速反舰导弹而言,浮空式角反射体的最大有效干扰距离要远大于反舰导弹的开机距离,因此,此时要以反舰导弹末制导雷达开机信号作为判断最大干扰距离的依据,且在该条件下,其有效干扰时间要小于50 s。 为验证上述分析的正确性,仿真舰艇脱离超声速反舰导弹导引头3 dB波束水平视场时所需的时间,仿真结果如图4所示。 图4 舰艇摆脱超声速反舰导弹跟踪最小时间统计Fig.4 Minimum time for warship getting rid of the supersonic anti-ship missile′s tracking 图4中,当反舰导弹末制导雷达开机距离为25 km,舰艇航行速度为25 kn时,诱饵在末制导雷达开机后24 s时与舰艇分离为2个目标,不再满足质心干扰的条件;若舰艇航速为15 kn,诱饵在末制导雷达开机后26 s时与舰艇分离为2个目标,不再满足质心干扰的条件。同理,当反舰导弹末制导雷达开机距离为30 km时,上述2种情况的分离时间变为29 s和31 s。 由此可见,上述几种条件下,舰艇摆脱反舰导弹跟踪的最小时间均小于50 s,且其有效干扰时间分别为24,26,29和31 s。与理论分析结果相吻合,再次验证了本文方法的正确性。 综上所述,不同的作战条件对浮空式角反射体质心干扰时机有很大的影响。在实际作战使用中,舰艇首先需要获取来袭导弹的距离、速度等信息,然后利用本文提出的方法快速推断出有效干扰距离,并在有效干扰距离内及时投放浮空式角反射体干扰弹,实现对来袭导弹的有效质心干扰。 本文通过理论分析与仿真验证相结合的方法对典型作战背景下浮空式角反射体质心干扰使用时机进行了分析研究,研究结果与思路可为浮空式角反射体干扰弹的实际使用提供一定的理论参考。在实际干扰作战中,留给舰艇做出反应的时间仅有数十秒,只有快速掌握敌方信息,准确把握投放时机,才能提高质心干扰的胜算。由于篇幅限制,本文只对干扰时机进行了研究,未来单舰反导作战中,影响无源干扰成功率的因素还有很多,下一步将会综合战场环境、舰艇机动等因素作进一步研究。4 浮空式角反射体质心干扰时机仿真验证
4.1 干扰亚声速反舰导弹仿真分析
subsonicanti-shipmissile

4.2 干扰超声速反舰导弹仿真分析


5 结束语

