三区域膜泡相分离模式之间转变的研究∗

2018-10-26 09:42纪丹丹张劭光

物理学报 2018年18期

纪丹丹张劭光

(陕西师范大学物理学与信息技术学院,西安 710119)

1 引言

20世纪70年代,德国物理学家W.Helfrich提出了生物膜的弹性曲率模型.他在研究红血球形状时,提出生物膜是处于液晶态这一观点[1],从液晶的Frank弹性自由能出发,推导出膜的曲率能Eb的表达式为[2]

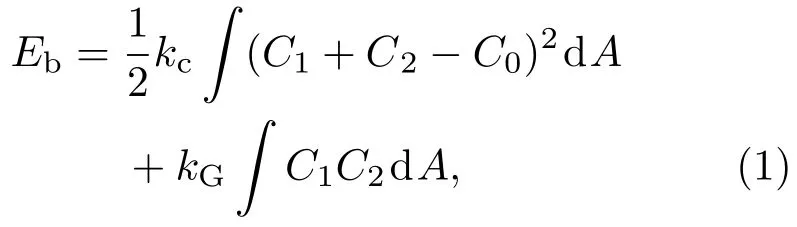
式中kc为曲面的曲率模量;kG为对应的高斯曲率模量;C1和C2分别为曲面上一点处的两个主曲率;C0为由类脂分子的不对称或膜泡两侧环境的不对称所引起的自发曲率;A为膜的总面积.根据微分几何中Gauss-Bonnet定理说明高斯曲率对闭合曲面的积分是一个与亏格n有关的常数.如果曲面的拓扑结构不变,那么就无需考虑与kG有关的那一项.

在一定温度及离子浓度下,A为常量;由于渗透压的作用,膜泡所包围的溶剂的总体积V通常也为常量.考虑这两个特性,可将闭合膜泡的总自由能F写为

式中∆P和λ分别是约束体积和面积为常数而引入的拉格朗日乘子.∆P可理解为膜泡内、外的渗透压,λ可理解为膜泡的有效表面张力.由于C0的存在,人们将此模型称为自发曲率模型.

Ouyang和Helfrich[3,4]通过对方程(2)的总自由能做变分,由总自由能的一阶变分δ(1)F=0,导出平衡时膜泡须满足的方程为

方程(3)是膜泡形状的普适方程,称为Ouyang-Helfrich方程.其中∆为曲面的拉普拉斯-贝尔特拉米(Laplace-Beltrami)算子,H=C1+C2/2为曲面的平均曲率,K=C1C2为曲面的高斯曲率.

真实的生物膜是由多种类脂分子和胆固醇构成(现不考虑蛋白质),由此形成膜上富含不同成分的区域,这些区域扮演着重要的生物学功能,此即生物膜的脂筏模型.人们相信脂筏的形成是由不同类脂分子的相分离导致的.关于球形膜泡相分离的实验研究已取得重要进展,人们发现由饱和磷脂分子、不饱和磷脂分子及胆固醇形成的巨型膜泡(giant vesicle),由于不同类脂分子之间的相互作用会导致相分离[5,6],形成由饱和磷脂分子和胆固醇构成的Lo相(liquid-ordered phase)子区域和由不饱和磷脂分子构成的Ld相(liquid-disordered phase)子区域.近年来Yanagisawa等[7]在球形膜泡相分离的基础上,加入山梨糖醇(sorbitol),改变膜泡两侧的渗透压,结果发现Lo区域发生向外或向内吐出很多芽(budding)的现象.剩下的球形母泡将发生进一步的相分离,变成三角海星形,最后变成凹盘形.凹盘形的上下两面进一步发生向外凸出,进而发生发芽形变.

多组分膜泡的总能量E是由曲率能Eb和边界的线张力能El两部分构成:

这里i表示多组分膜泡的不同相(Lo相或Ld相),k(i)表示两相的曲率模量,σ为两相边界处的线张力系数.

多组分膜泡相分离行为是由Lo相的曲率模量ko和Ld相的曲率模量kd以及两相边界处的线张力系数σ决定.通常引入ko和kd的比值ε=ko/kd来表示两相曲率模量的相对强度,其中ko和kd的量级都为1×10−19J,而目前认为ε一般为1.25—4[6,8].

多组分膜泡的稳定形状仍然遵守Ouyang-Helfrich方程,只是在两相边界处需要加额外的边界条件.由于(4)式中膜泡的总能量具有标度不变性,所以(2)式中描述膜泡大小的参量A和V只有一个是独立的,通常引入无量纲的约化体积v(或过剩面积ξ)来描述这个量.为此先定义约化半径

则约化体积v可定义为

可见v6 1,对于球形v=1.过剩面积ξ表达式为

对于球形ξ=0,随着ξ的增大,膜泡偏离球形就越远.对于同一分支解,具有相同的v(或ξ)但大小不同的膜泡总是有相似的形状和相同的曲率能Eb.因此只需要一个参量v(或ξ)就可以表示A和V这两个变量.同时v和ξ都可表示膜泡形状偏离球形的程度,二者之间的关系为

同时定义约化线张力系数

2010年,Yanagisawa等[9]在通过实验发现了多组分膜泡相分离成两相三区域的有趣现象,同一相可能分布在两个区域.如果用Ao表示Lo相的面积,Ad表示Ld相的面积,定义面积分数ϕo表示Lo相的面积占总面积A的比例,则有

实验发现,对于ξ<0.1(即v>0.75)的管状巨型膜泡,在经历相分离后能转化成两种模式的三区域膜泡:当ϕo>0.5时,膜泡转变为中间有一个Lo域的长椭球,称为相分离模式I;当ϕo<0.5时,膜泡转变为上下有两个Lo域的扁椭球,称为相分离模式II(参见图1).另外实验还观测到了Lo和Ld相呈周期性调制的细管状膜泡,本文重点研究三区域膜泡.为了解释实验上观察到的现象,Yanagisawa等[9]用几何上椭球的参数方程近似代表膜泡的形状,在此基础上估算出两种形状下对应膜泡的总能量,计算得到的相变点为=0.27,但这与实验上的结果=0.5差别很大.这种差别是由于他们所采用的近似计算方法的缺陷导致的,还是涉及膜泡弹性曲率模型的适用性问题呢?也就是基于Helfrich自由能的曲率弹性模型能否对三区域膜泡的稳定形状及相分离的实验结果给出满意的解释,是本文将要研究的问题.

在实验上,多组分膜泡边界的σ值大约介于0.01—5 pN之间[7,10−12],膜泡的半径如取5µm,根据(11)式估算出介于0.5—250之间.Yanagisawa等[9]估算出实验环境对应的约化线张力系数¯σ≈50.在如此大的约化线张力系数下,膜泡对应的稳定形状是什么,目前还没有相关文献报道.本文基于Helfrich自由能的曲率弹性模型,用直接极小化方法对相关问题进行研究,探究能否给出与实验符合的相变点.

Yanagisawa等[9]的实验分为两个过程.上文讨论的相分离模式I和II的稳定形状可以保持几十分钟,然后就开始向长椭球转变,经过几十秒后变成发芽的形状(颈部很细的形状).目前文献中还没有对该相变发生的机制及必要条件进行讨论,这是本文的另一个研究重点.本文通过直接极小化的计算表明,只有保证膜泡内外溶剂可以自由渗透,即约化体积可以自由改变,才可能发生发芽形变.至于膜泡内外渗透发生的机制,或是非常大的约化线张力系数导致的在两相边界处的临时缺陷,因而造成溶剂的临时通道,该假设还需要实验的检验.

2 计算方法

对膜泡稳定形状的求解有两种方法,一种是直接求解Ouyang-Helfrich方程;另一种是在给定约束下,用直接极小化Helfrich曲率能的方法来给出稳定形状.

求解方程(3)可采用解析方法和数值方法.但由于方程(3)是高阶非线性偏微分方程,很难直接求解,目前只知道一些特解,包括克利福德锚环解[13]、红血球解[14]以及扩展的Delaunary曲面解[15].因此人们通常使用数值方法,通过积分形状方程来研究膜泡形状.对于具有旋转对称性的多组分膜泡,Ouyang-Helfrich方程仍然成立,只需要在两相的边界上加上相应的边界条件就可以转化为两点边值问题[16].Jülicher等[17]曾研究具有旋转对称性的两区域膜泡的相分离.周五斌和张劭光[18]也通过双向“打靶法”研究了旋转对称的两区域膜泡在不同ε和下的平衡形状.

当所研究的膜泡形状不一定具有旋转对称性时,膜泡的形状方程为高阶非线性偏微分方程,目前还没有数值积分的方法,因此人们在研究非旋转对称的膜泡形状时会根据实际问题采用一定的近似.但由于Helfrich变分问题的不同分支解的能量经常会非常接近,因而这种近似方法往往得不到正确的结果,正如文献[9]中把膜泡形状简单用椭圆参数方程表示无法给出与实验符合的结果.

目前对一般的(不一定具有旋转对称性)膜泡较精确的数值计算是采用有限元法,通过直接极小化自由能来确定膜泡的形状.这方面的工作多数采用Surface Evolver软件,它是由Brakke教授[19]基于C语言开发的一个交互有限元模拟软件,可以在网上下载.它可以计算曲面在各种约束条件下,使表面张力能及其他能量极小化时曲面的形状,有一套编程语言,使用者能根据计算内容自由灵活地编程.并可根据需要加入要计算的新能量.该软件自发布后经近20多年的不断完善,现已被广泛的用于微分几何、化学以及凝聚态物理中的晶粒生长等诸多领域.

目前关于相分离的实验结果还不多,文献[9]的实验结果是一重要突破,而目前还没有针对该实验的满意的理论解释.Gutlederer等[20]用Surface Evolver软件,在一定的参数区间内对多组分膜泡能形成的模式进行了较详细的研究,但目前还没有针对文献[9]中的实验条件的计算结果,特别是较大的¯σ值时的计算结果.

根据实验上观察到的三区域膜泡,本文建立了如图1所示的两种模式的初始形状(本文图都是用黑色区域表示Lo相,灰色区域表示Ld相):1)中间是Lo相的区域,Ld相分为上下两个区域,称为相分离模式I,对应实验上观察到的长椭球形;2)Lo相分为上下两个区域,中间是Ld相的区域,称为相分离模式II,对应实验上观察到的扁椭球形.

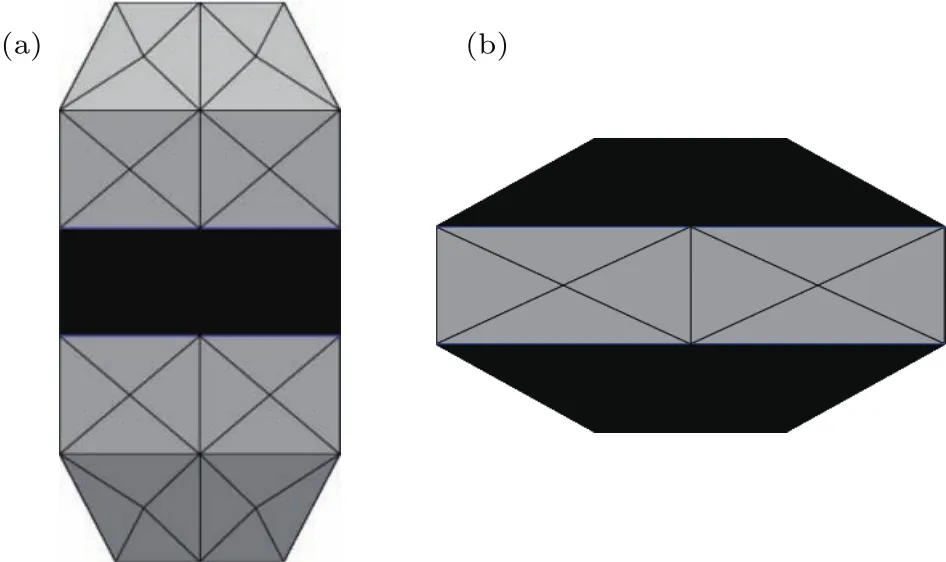
图1 两类初始模型 (a)相分离模式I;(b)相分离模式IIFig.1.Two types of initial model(The black and gray regions represent the Lophase and Ldphase respectively):(a)Phase separation pattern I;(b)phase separation pattern II.

在Surface Evolver软件中,膜泡的曲率能可表示为

在三区域膜泡的计算中有一个困难,为了解决两区域的边界线的光滑性,在Surface Evolver的计算中要把两区域的边界线固定在一个平面上,而图1中的三区域膜泡具有两个边界线,因此需要把它们固定在两个平面上.因为这两个平面的距离是预先给定的,如果再对这两个平面之间的Lo相或Ld相的面积加上约束值,就会产生约束过多的问题,从而得不到实际想要的计算结果.以往研究的两相两区域膜泡由于只有一个边界,就不存在该困难.

为了解决上述三区域膜泡计算中的困难,注意到膜泡的曲率能具有标度不变性,即形状相似但大小不同的膜泡具有相同的曲率能[16,18,21].该关系虽然是对单组分膜泡得到的,但可证明其对多组分膜泡仍成立,具体细节可参见附录A.第1节已经指出形状相似但大小不同的膜泡,只要其约化线张力系数¯σ是相同的,就具有相同的线张力能.因此,在实际计算中并不分别给定两相各自的总面积,而是让其比值满足设定值ϕo(定义见(12)式)即可,这样就给出了膜泡在相似的形状之间变化的自由度.在膜泡的演化过程中,不断对ϕo施加约束,而Lo或Ld相的实际面积可以变化,因而膜泡的大小可以自由变化,这样就可得到满足设定值ϕo的结果,从而解决了约束过多的问题.在计算的每一步都根据最新的面积值,由(11)式重新设定σ值,使得¯σ保持在本文需要计算的值.另外根据约化体积的定义(10)式,注意到相似形状的约化体积是相同的,因此可以在改变膜泡的面积和所包围的体积的情况下,保持约化体积不变.具体可以在Surface Evolver下通过定义一个量(quantity),来对约化体积v施加约束,而不必分别固定膜泡的体积和面积.

总之在计算中是固定两相的面积比ϕo和约化体积v,但其计算结果和分别固定两相的面积Ao和Ad及所包围体积V的计算结果是完全一致的.

三区域膜泡的总能量可由三个区域的曲率能和两个边界的线张力能的总和得到(见(4)式).在本文计算中,暂取三区域膜泡的自发曲率和高斯曲率模量为零,膜泡的总能量以8πkd为单位.

通过实验观察到的三区域膜泡都是具有上下对称性的,因此只对上下对称的膜泡(见图1)进行了计算,这大大减小了计算量.

3 有体积约束时的计算结果

本节在计算中给定Lo相和Ld相的面积比ϕo并加上对约化体积v的约束.根据第2节讨论,这种计算结果与给定两相各自的面积,并加上体积约束的计算结果是一致的.本文重点讨论不同¯σ值,特别是很大时两种模式的稳定形状.为了与文献[9]中的计算结果进行对比,本文在进行数值模拟时,取过剩面积ξ=0.02(由(10)式可得对应的v≈0.942),弹性模量比ε=1.25.

图2 当=0.5时,在两种模式(实线表示模式I,虚线表示模式II)下膜泡的归一化总能量E/(8πkd)与ϕo的关系,图中给出了在ϕo=0.25,0.4,0.55时模式I和模式II对应的稳定形状Fig.2.Normalized total energy curves of pattern I(solid line)and pattern II(dotted line)with=0.5 as functions of ϕo.The stable shapes of pattern I and pattern II with ϕo=0.25,0.4 and 0.55 are also shown.

3.2 中等值时膜泡的稳定形状

随着约化线张力系数的增大,线张力能逐渐对膜泡的形状起到了重要的支配作用.这时在两种相分离模式下的稳定形状都是长椭球形.图3给出了当¯σ=5.0时,两种模式下膜泡的总能量随ϕo的变化,对于一些典型的ϕo值,还给出了两种模式下膜泡的稳定形状.可以看出两种相分离模式的相变点为=0.45. 当ϕo<0.45时,模式II的长椭球能量低,是稳定的.当ϕo>0.45时,模式I的长椭球是稳定的.

图4(a)和图4(b)分别给出在两种相分离模式下,膜泡的曲率能及线张力能与ϕo的关系.实线代表膜泡曲率能,虚线代表膜泡两相边界处的线张力能.从图4可以看出,当=5.0时,在两种模式下膜泡的曲率能都已显著小于线张力能.这时线张力能对膜泡的形状已有重要的支配作用,为减小两相的边界长度,从而减小线张力能,在相分离模式II下的稳定形状已变为长椭球形.为了保证结果的可靠性,本文特意选取不同的初始形状(包括扁椭球),结果最后都演化到了长椭球.

图3 当=5.0时,在两种模式(实线表示模式I,虚线表示模式II)下膜泡的总能量E/(8πkd)与ϕo的关系,图中展示了在ϕo=0.3,0.5,0.7时膜泡的稳定形状Fig.3.Normalized total energy curves of pattern I(solid line)and pattern II(dotted line)with=5.0 as functions of the area fraction of the Lophase ϕo.The stable shapes for ϕo=0.3,0.5 and 0.7 are also shown.

图4 两种模式下,膜泡的归一化曲率能Eb/(8πkd)(实线)及线张力能El/(8πkd)(虚线)与ϕo的关系 (a)模式I;(b)模式IIFig.4.Normalized bending energy Eb/(8πkd)(solid line)and normalized line energy El/(8πkd)(dotted line)curves of two patterns with¯σ=5 as functions of ϕo:(a)Pattern I;(b)pattern II.

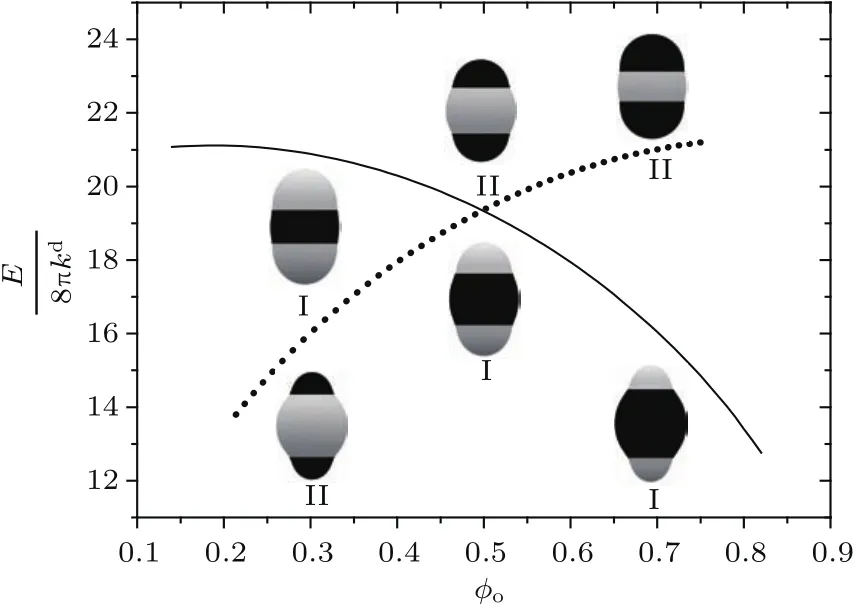
图5 =50时,在两种模式(实线表示模式I,虚线表示模式II)下膜泡的归一化总能量E/(8πkd)与ϕo的关系,图中也给出了在ϕo=0.3,0.5,0.7时膜泡的稳定形状Fig.5.Normalized total energy curves of pattern I(solid line)and pattern II(dotted line)with=50 as functions of ϕo.The stable shapes for ϕo=0.3,0.5 and 0.7 for the two patterns are also shown.

类似图5呈现的膜泡形状确实在实验中也被观察到(参见文献[9]中图1和图2).另外发现在有约化体积约束时,即便对应¯σ=50这么大的约化线张力系数也不会发生发芽形变,只是在两相边界处发生一定程度的内箍.这是由于膜泡不但受到v的约束,还受到面积分数ϕo的约束,而线张力能引起的发芽现象总是发生在两组分的交界处,因此对给定ϕo,只有特定的约化体积v才能使膜泡发生发芽形变(详细讨论见第4节),同时给定ϕo和v一般不能发生发芽形变.而单组分膜泡由于没有ϕo的约束,在给定v的情况下,就能发生发芽形变[21].

4 无体积约束的计算结果

本节将探讨什么条件能使三区域膜泡发生发芽形变.只有去掉了约化体积的约束(这相当于允许膜泡两侧可以自由渗透),且当>7.0时,膜泡才会演化到类似实验上观察到的发芽状态.

在数值模拟过程中,同样建立两种模式,取ε=1.25,ϕo=0.5,在相同的ϕo值下研究¯σ对膜泡稳定形状的影响.图6(a)和图6(b)分别给出了在不加体积约束时,在相分离模式I及模式II下对应不同¯σ值的稳定形状.可以看出,在不加体积约束时,对应不同的¯σ值,稳定形状差别很大.随着¯σ的增加,两种模式下稳定膜泡的两相边界处截面圆的半径越来越小.

图6 无约化体积约束且固定ϕo=0.5时,不同约化线张力系数下计算的膜泡的稳定形状及对应的约化体积(a)相分离模式I;(b)相分离模式IIFig.6.Stable shapes and corresponding reduced volumes of vesicle calculated for several reduced line tension in the case of ϕo=0.5 without reduced-volume constraint:(a)Phase separation pattern I;(b)phase separation pattern II.

当¯σ>7.0时,膜泡的稳定形状差别已不大,已接近无穷小颈部的极限形状,即发芽形状.

图7 去掉约化体积约束且ϕo=0.5,¯σ=7.0时,两种模式下膜泡形状的演化过程 (a)相分离模式I;(b)相分离模式IIFig.7.Shape evolution process for ϕo=0.5 and¯σ=7.0 without the constraint of reduced volume under two patterns:(a)Phase separation pattern I;(b)phase separation pattern II.

对应以上演化过程中的任意一步给出了演化过程中间形状对应的约化体积v.在这些中间形状中,如果对v重新加上约束则膜泡向发芽过程的相变就会停止.而如果再逐渐地增大约化体积,膜泡还会演化回粗颈的形状.可见同时施加v和ϕo的约束,膜泡一般不会出现发芽形变,除非v的约束值碰巧等于该ϕo值下发芽形状的值,例如v的约束值取0.592时(见图7(a)N=60000的膜泡形状).也就是说去掉体积的约束是发芽形变发生的关键因素.因此本文认为实验上观察到的发芽形变应该是在没有约化体积约束的情况下得到的.

从以上讨论可以看出,多组分膜泡的发芽形变和单组分膜泡的发芽形变是截然不同的.以往人们对单组分膜泡的研究发现,发芽可以发生在固定约化体积的情况下,例如在自发曲率模型下改变自发曲率,或在双层耦合模型下改变双层面积差[21].

上述对三区域膜泡的研究得到实验观察到发芽形状的两个条件:一是足够大(>7.0);二是去掉约化体积的约束.单纯增大¯σ值并不能发生发芽形变(见图5),这是因为多组分膜泡有一个两相面积比ϕo的约束(合理的假设是该值不发生改变),如果在ϕo的约束下再施加对v的约束,通常是不可能发生发芽形变的.计算表明只有允许膜泡内外溶剂可以自由渗透,约化体积可以发生改变时,才能发生发芽形变.

5 结论

本文研究了有约化体积约束和无约化体积约束两种情况下,ε=1.25,不同¯σ值时,三区域膜泡的两种相分离模式的稳定形状,及其之间的相变.

在有约化体积的约束时计算发现如下结论.

2)相分离模式I的膜泡的稳定形状总是长椭球形,而相分离模式II的膜泡的稳定形状并不一定是扁椭球形.当ε=1.25,ξ=0.02(对应v=0.942)时,计算表明,当较小时,在相分离模式II下的稳定形状是扁椭球形.随着的增大,当=5.0时,在相分离模式II下的稳定形状已变为长椭球形,当达到50时,线张力能远大于曲率能,这时相分离模式II下的稳定形状一定是长椭球形.这不同于Yanagisawa等[9]认为模式I一定对应长椭球形,模式II一定对应扁椭球形的观点.

为了说明实验观察到的发芽现象,本文在不加约化体积约束的情况下进行了计算,得到发生发芽的两个必要条件:较大的约化线张力系数(>7.0)和无约化体积约束(即允许膜泡内外溶剂可以自由渗透).通过对实验上的发芽形变过程进行分析,也可发现与本文计算结果类似的形状变化过程.目前已有文献中并没有注意到发芽过程中约化体积发生了改变,也没有关注该自由渗透的产生机制.我们猜测是非常大的约化线张力系数导致的两相边界处的临时缺陷,因而造成溶剂的临时通道.当然这只是一种可能性,该假设还需要实验的检验.

最后还须指出,实验观察到的三区域膜泡都是具有上下对称性的,因此只对上下对称的膜泡进行了计算,这大大减小了计算量.文献[9]用椭球参数化膜泡时也预先假定了膜泡的上下对称性.至于上下不对称的膜泡以及两区域膜泡为何在实验中没有被发现,目前原因还不清楚.

附录A 两个相似形状的膜泡的曲率能和线张力能相等的条件

考虑一个曲面r(u,v),其中黑色区域代表Lo相,灰色区域代表Ld相,共有三个区域:D1,D2,D3,这些区域有两个边界B1和B2.

对该曲面做相似变换,其中α为一实数.则是相似形状.也有三个区域:,这些区域有也两个边界

设r(u,v)各点处的平均曲率为H,面积元为dA,总面积为A,约化半径为边界处线元为dl.曲面r′(u,v)各点处的平均曲率为H′,面积元为dA′,总面积为A′,约化半径为边界处线元为 dl′.则有