反应扩散系统中反螺旋波与反靶波的数值研究∗

倪之玮 李新政 白占国 李燕

(河北科技大学理学院,石家庄 050018)

1 引 言

螺旋波斑图是非线性系统中自组织形成的时空有序结构,是自然界中最常见和最基本的一种远离平衡态的斑图形式,它广泛地存在于自然界和各实验系统中[1−5],根据传播形式可分为螺旋波(spiral)和反向螺旋波(antispiral).螺旋波(运动形式由波头向外传播的螺旋波)由于其广泛存在和容易形成被人们所熟知,国内外学者已对其进行了系统的实验及理论研究,并发表了大量的研究结果.人们通过分析多个系统中的单臂螺旋波的性质及其动力学行为,系统地研究了单臂螺旋波的破缺机制和控制方法[6−12],并对复杂的多臂数螺旋波和超级螺旋波也从理论模拟和实验上进行了多方面的研究[13−19].而反螺旋波(运动形式由外向波头反方向传播的螺旋波)直到2001年Vanag和Epstein[20]在BZ-AOT化学反应系统中发现,才被命名,随后开始引起人们的注意与研究.Gong和Christini[21]通过模拟发现反应扩散系统在霍普失稳附近会出现反螺旋波;Wang等[22]发现弛豫振荡介质中远离霍普失稳时以及单相反应扩散系统在临近霍普失稳时也可以自发出现反螺旋波;Nicola等[23]利用复Ginzburg-Landau理论方程讨论了反应扩散系统在霍普失稳附近产生螺旋波与反螺旋波的区别;Qian等[24]利用耦合FitzHugh-Nagumo(FHN)模型研究了多普勒失稳造成稳定反螺旋波到湍流态的演化.鉴于反螺旋波的研究起步较晚,目前相关研究结果相对较少.研究不同失稳时系统出现的反螺旋波以及反螺旋波的多样性,将有助于人们对反螺旋波的了解.

本工作采用三变量Brusselator扩展模型,分析了反应扩散系统反螺旋波与反靶波的产生机制与时空特性,并对反应扩散系统中的反螺旋波与反靶波以及多臂反螺旋波的形成及其转化过程进行了数值分析,其研究结果对于丰富和深入理解反螺旋波和反靶波的理论具有一定的参考意义.

2 理论模型

目前,用于研究螺旋波斑图的理论模型主要有复Ginzburg-Landau方程、三变量Purwins模型、Barkley模型、FHN模型和Bär模型等.本工作采用三变量Brusselator扩展模型[25],其无量纲的形式如下:

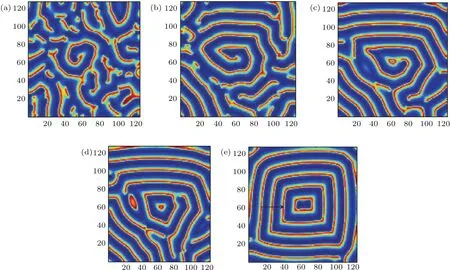
式中,U,V和W分别为活化子和禁阻子以及不活跃中间物质的浓度;DU,DV,DW分别表示三个变量的扩散系数(DU

解此特征方程可以得到色散关系:

利用色散关系可以判断系统的失稳特性,进而可知系统形成斑图的时空特征.当Im(λ)=0,Re(λ)=0(k=kT=0)时,系统发生图灵失稳,形成空间上周期性分布的静态斑图;当Im(λ) =0,Re(λ)=0(k=0)时,系统经历霍普失稳,形成随时间周期变化的均匀动态斑图;当Im(λ) =0,Re(λ)=0(k=kw=0)时,系统经历波失稳,产生时间和空间上都具有周期性的动态斑图.

在本文的数值模拟中,采用欧拉向前差分的方法进行积分,数值模拟在一个含有N×N(128×128)个格子的二维平面上进行,时间积分步长为∆t=0.01个时间单位,边界条件选用零流边界条件,为确保其稳定性所有结果的积分时间均超过2000个时间单位.

3 数值模拟结果与分析

3.1 反螺旋波的形成机制

非线性系统发生霍普失稳或波失稳时系统的均匀性会遭到破坏,从而引起物质浓度的变化,系统形成随时间变化的空间动态斑图.模拟研究发现反应扩散系统不仅在霍普失稳、波失稳附近产生反螺旋波,并且在霍普失稳与波失稳共同作用下也可以形成多种反向螺旋波.图1是系统参数(a,b,c,d,Du,Dv,Dw)在(2.0,7.0,1.0,1.0,0.5,1.0,8.0)附近时,形成的单臂反螺旋波.从色散曲线进行分析,可以看出系统在经历霍普失稳的同时发生波失稳,且霍普模的强度hf大于波失稳处模的强度hw,因此霍普失稳占主导地位,而波失稳相对较弱,系统可形成随时间和空间周期变化的动态斑图.由于反螺旋波的群速度vg>0(图1(c1)),所以其波源成为中心位置的拓扑缺陷点,而由于波的传播方向由外向内,与螺旋波的方向相反,所以相速度vp<0,因此可判断反螺旋波的色散关系为负[23,25,26].从反螺旋波的形成过程(图1(a2)—(e2))可以看出:二维模拟系统首先随机产生随时间变化的空间动态点状斑图,随模拟时间的延长,不同动态点状斑图间相互碰撞融合,逐渐演化成动态线状条纹斑图,由于条纹斑图不同位置的波速不同,边缘端点的波速小于中间位置点的波速,条纹逐渐变为蜷曲状,一个端点形成波头,在局部形成反螺旋波的初始形态,随模拟时间的延长最终演化成产生于边界、波由外向内传播、消失于中心的单臂反螺旋波.图1(d2)和图1(e2)是同一周期中波头的不同相位,两图的时间间隔约为T/4,从图中可以看出单臂反螺旋波的走向与波头的相位运动方向相同,均为逆时针,这与所熟悉的单臂螺旋波的情况相反,是波由外向内的反向传播造成.经过多次模拟发现反螺旋波的波头在旋转过程中表现出与螺旋波相同的运动特点,如运动轨迹为定点、圆形、漫游等.此外,系统还可观察到同向和反向转动的偶极子反螺旋波对.

图1 单臂反螺旋波的色散关系曲线及形成过程 (a1)色散的实部Re(λ)曲线;(b1)色散的虚部Im(λ)曲线;(c1)虚部的导数曲线;(a2)—(e2)为单臂反螺旋波的形成过程(模拟时间顺序:13.9,577.3,657.7,1279.6,1280.3)Fig.1.Dispersion relation curves and forming process of single-arm antispral:(a1)The real part of dispersion;(b1)the imaginary part of dispersion;(c1)the first derivative of the imaginary part;(a2)–(e2)the forming process of single-armed antispiral(The simulation time sequence is as follows:13.9,577.3,657.7,1279.6,1280.3).

图2 反螺旋波变量的时空分布 (a)三变量的时间分布(选取时间间隔5000—6000);(b)三变量的空间分布Fig.2.Spatio-temporal distribution of variables:(a)The time distribution of the three variables(The selected time interval is between 5000 and 6000);(b)the spatial distribution of the three variables.

图3 反靶波的色散关系曲线及靶波的形成过程 (a1)色散的实部Re(λ)曲线;(b1)色散的虚部Im(λ)曲线;(c1)虚部的导数曲线;(a2)—(e2)为靶波的形成过程截图(模拟时间顺序:13.8,75.8,121,200.2,5284.8)Fig.3.Dispersion relation curves and forming process of antitarget wave:(a1)The real part of dispersion;(b2)the imaginary part of dispersion;(c1)the first derivative of the imaginary part;(a2)–(e2)the forming process of antitarget wave(The simulation time sequence is as follows:13.8,75.8,121,200.2,5284.8).

利用u,v,w三个变量的浓度随时间和空间的变化对单臂反螺旋波的时空特性进行分析.从变量随时间和空间的变化曲线(图2)可以看出:三者均随时间做周期性振荡,在空间上也是周期性分布的,且两图中三变量的峰值出现的位置不同,这是由于三变量具有不同的时间尺度和扩散速度造成的.从变量的时空特征可以判断反螺旋波是一种时间上振荡,空间上呈周期性分布的时空斑图.

3.2 反靶波的形成机制

系统不仅可以生成反螺旋波,还可以生成向里传播的反靶波.图3是系统参数(a,b,c,d,Du,Dv,Dw)在(2.0,7.5,1.0,1.0,0.4,1.0,8.0)附近时,二维模拟系统形成的反靶波斑图.通过对色散关系曲线分析,发现系统在经历霍普失稳和波失稳的同时还经历了图灵失稳,并且霍普模的强度hf和图灵模的强度hT远大于波失稳处模的强度hw,因此系统以霍普失稳和图灵失稳为主,而波失稳相对较弱,系统在多种失稳的共同作用下可形成复杂运动形式的动态斑图.由于反靶波的群速度vg>0(图3(c1)),所以中心为波源,与螺旋波和反螺旋波的位置相同;又因波的传播方向与反螺旋波相同——由外向内传播,所以相速度vp<0,由此可判断反靶波的色散关系为负.经研究发现反靶波的形成过程与反螺旋波不同,二维模拟系统首先在某些区域出现强度周期变化的无规则点状斑图,空间位置基本不变.随模拟时间延长,其中几个区域周期变化的点状斑图逐渐突显,并影响到整体,二维模拟空间在这几个区域逐渐形成靶源,并形成由外向靶心传播的多个自持续反靶波,多个反靶波间通过相互影响,最终二维模拟系统形成单一中心的反靶波,但由于受模拟边界及空间位置的影响,形状为圆形的反靶波最终演化成方形反靶波.

通过大量模拟发现:在一定条件下单臂反螺旋波也可以转化成反靶波,此过程初始阶段与二维系统直接形成反靶波不同,而与反螺旋波的过程相同.从图4可以看出,系统首先由无规则动态点状斑图演化成动态条纹斑图,进而形成单臂反螺旋波斑图,但所形成的反螺旋波斑图的波头较为特殊,在随模拟时间延长过程中,波头区域会逐渐增大,在旋转过程中由于其波速较低,会与反螺旋波的临近部位相碰撞,并在此位置截断反螺旋波,原波头区域会形成一个自持续的周期性靶源,从而在局部区域形成不规则的反靶波,随模拟时间延长,二维模拟系统最终形成反靶波斑图.

图4 单臂反螺旋波向反靶波转化过程(模拟时间顺序:702.7,2115.8,3605,4164.9,4739.4)Fig.4.Conversion process of single-armed antispiral to anti-target wave(The simulation time sequence is as follows:702.7,2115.8,3605,4164.9,4739.4).

3.3 多臂反螺旋波的时空特性及其转化

通过数值模拟获得了单臂、双臂、三臂等多种不同臂数的反螺旋波斑图.图5为二维模拟系统获得的双臂到六臂的反螺旋波斑图.从图5可以看出,波传播方向均由外向里,波头的相位运动方向与反螺旋波的走向相同,旋转方向随机,可为顺时针或逆时针方向,除三臂反螺旋波的波头顺时针转动外,其余则为逆时针转动.研究发现,反螺旋波随臂数的增加,不仅波头的动力学行为更加复杂,而且中心区域的半径也逐渐增大,这与实验系统系统对多臂螺旋波研究结果相一致[27].

图5 不同臂数反螺旋波斑图(其余固定参数:a=3.0;b=11.39;c=d=1.0) (a)双臂(Du=0.5,Dv=1.0,Dw=23.0);(b)三臂(Du=0.6,Dv=1.0,Dw=25.0);(c)四臂(Du=0.7,Dv=1.0,Dw=25.0);(d)五臂(Du=0.45,Dv=1.0,Dw=40.0);(e)六臂(Du=0.6,Dv=1.0,Dw=26.0)Fig.5.Various kinds of multi-armed antispiral patterns(Parameters:a=3.0;b=11.39;c=d=1.0):(a)Two arms(Du=0.5,Dv=1.0,Dw=23.0);(b)three arms(Du=0.6,Dv=1.0,Dw=25.0);(c)four arms(Du=0.7,Dv=1.0,Dw=25.0);(d) five arms(Du=0.45,Dv=1.0,Dw=40.0);(e)six arms(Du=0.6,Dv=1.0,Dw=26.0).

在模拟多臂反螺旋波过程中,发现不同臂数反螺旋波的波头运动规则不同,并且波头间的碰撞顺序与波头的旋转方向有关.图6是双臂与三臂反螺旋波的波头逆时针旋转运动的情况,可以看出:波头的转动方向都与波的走向相同,双臂反螺旋波的动力学行为相对比较简单(图6(a1)—(d1)),在T/2周期内两臂的波头不断发生碰撞和远离,且绕着同一个中心点做周期性运动,旋转过程中每半个周期两旋转臂的波头碰撞一次,两个波头位置总是关于中心点对称分布,这就意味着双臂反螺旋波的两个波头相位差始终保持π;三臂反螺旋波的波头具有非常复杂的动力学过程(图6(a2)—(d2)),由于相邻两臂的相位差为2π/3,所以旋转臂失去了对称性,在T/3周期内波头碰撞两次,它的三个波头端点两两相互碰撞,顺序为1-3-2-1的逆时针排序.由于多臂螺旋波的波头在不停地碰撞和远离,所以随着臂数的增加,四臂、五臂和六臂反螺旋波的波头运动情况更为复杂,并且发现随臂数的增加,波头的旋转运动周期逐渐增大,其原因可能与中心区域的旋转半径有关.

通过观察不同情况的多臂反螺旋波发现,在一定模拟条件下多臂反螺旋波经历一段时间后,其中的一个旋转臂会逐渐远离波头中心区域,并逐渐消失,系统形成一个新的臂数少一的反螺旋波斑图.图7是逆时针旋转的反螺旋波从四臂→三臂的转化过程,可以看出:四臂反螺旋波中心波头的旋转及相互碰撞比双臂与三臂反螺旋波运动更加复杂,在波头旋转运动的过程中其中心会发生缓慢的移动,从而使四臂反螺旋波逐渐失去了空间旋转不变对称性;同时由于它的中心四个端点也在不断地相互作用,造成其中的一个旋转臂逐渐远离旋转中心区域,并在边界条件的限制下逐渐消失,二维模拟系统形成一个新的三臂反螺旋波.分析其原因主要是由于微扰的作用或者其他条件的影响,使位错的拓扑荷符号与反螺旋波的拓扑荷符号相反造成的.图7中四臂反螺旋波为逆时针走向时,因与螺旋波运动方向相反,所以其拓扑荷符号应为负值;而反螺旋波的波头相位运动方向同为逆时针,因此位错的拓扑荷符号为正值.此外,还发现多臂反螺旋波在一定条件下可以实现从多臂到单臂的连续转化.

图6 双臂与三臂反螺旋波波头的旋转运动情况 (a1)—(d1)双臂模拟时间顺序分别为 3424.5,3425,3425.7,3426.3;(a2)—(d2)三臂模拟时间顺序分别为3074.7,3075.3,3075.7,3076.2Fig.6.Rotating motion of the wave tips with two arms and three arms.(a1)–(d1)the simulation time sequence of twoarmed antispiral is as follows:3424.5,3425,3425.7,3426.3.(a2)–(d2)the simulation time sequence of three-armed antispiral is as follows:3074.7,3075.3,3075.7,3076.2.

图7 四臂反螺旋波向三臂反螺旋波转化过程(模拟时间顺序:2405.9,2529.9,2648.1,2895.8,3190)Fig.7.Conversion process of four-armed antispiral to three-armed antispiral(The simulation time sequence is as follows:2405.9,2529.9,2648.1,2895.8,3190).

3.4 系统参数对反螺旋波和反靶波的影响

由于斑图的形成与稳定性依赖于参数的选取,因此研究系统参数对图形的影响非常重要.文中在一定范围内研究了控制参数a,b以及扩散系数对斑图的影响:通过对比发现控制参数a,b的连续变化可引起反螺旋波空间尺度的规律变化,随a的增加反螺旋波逐渐变稀疏(图8(a1)和图8(b1)),而随b的增加反螺旋波逐渐变密集(图8(c1)和图8(d1)),并且参数a的可变化范围远小于b.扩散系数虽对斑图的空间尺度没有明显的影响,但发现扩散系数Dw持续增加到一定值时,波的传播方向会发生改变,由向内传播改为向外,二维模拟系统形成的反螺旋波与反靶波会被螺旋波和靶波所取代(图8(a2)—(d2)),且随Dw的增大反螺旋波不仅会转为同臂数的螺旋波,还可形成不同臂数的螺旋波.利用色散曲线分析其原因发现,随Dw的增加,系统的波失稳程度逐渐增大,当波失稳达到一定程度时,波速vg为正值,从而导致了系统斑图属性的改变.因此得出系统在临界波失稳附近时可形成反螺旋波和反靶波,而在远离波失稳时易形成螺旋波和靶波.

图8 系统参数变化对斑图的影响 (a1),(b1)a变化时波空间尺度对比(a=1.95,2.05);(c1),(d1)b变化时波空间尺度对比(b=6.5,7.0);(a2),(b2)反螺旋波到螺旋波的转变(Dw=6.0,19.0);(c2),(d2)反靶波到靶波的转变(Dw=8.0,10.0))Fig.8.In fluence of system parameter variation on the pattern:(a1),(b1)Wave space scale changes induced by parameter a(a=1.95,2.05);(c1),(d1)wave space scale changes induced by parameter b(b=6.5,7.0);(a2),(b2)the transformation of antispiral to spiral induced by parameter Dw(Dw=6.0,19.0);(c2),(d2)the transformation of antitarget wave to target wave induced by parameter Dw(Dw=8.0,10.0).

4 结 论

本文利用三变量Brusselator扩展模型对反应扩散系统中反螺旋波和反靶波进行了数值研究,并与螺旋波的研究结果进行了对比,发现其形成机制和时空特性具有与螺旋波相同的特征,如失稳特征、时空的周期性、波头运动轨迹的多样性等,同时还发现反螺旋波的波头旋转方向与波的走向相同这一点与螺旋波不同,考虑其原因是反螺旋波由外向内传播方式造成的.除霍普失稳外,系统得到在超临界波失稳附近生成的多种反螺旋波.通过改变参数获得了多种不同臂数的反螺旋波,发现随臂数的增加,波头的运动特点更为复杂,且波头的旋转周期随臂数的增加逐渐增大.在一定的模拟条件下,由于受微扰及边界条件因素的影响,多臂数的反螺旋波可以向臂数少的反螺旋波发生转变,并可实现单臂反螺旋波到反靶波的转化.通过研究系统参数对斑图的影响发现:控制参数a,b对反螺旋波与反靶波的空间尺度影响比较明显,而与参数a,b持续增大造成波空间尺寸变化的效果相反;扩散系数Dw的持续增加会造成波失稳程度的增大,并导致波速符号发生变化,从而系统斑图出现反螺旋波到螺旋波以及反靶波到靶波的转变.本文的研究结果不仅丰富了反螺旋波的相关理论,对于深入研究反螺旋波和螺旋波的相互联系也具有重要的借鉴作用.