基于RBF神经网络的永磁同步电动机PID控制

邵文强，康尔良

(哈尔滨理工大学，哈尔滨 150080)

0 引 言

永磁同步电动机(以下简称PMSM)因具有结构简单、损耗低、功率密度高等优点，广泛应用于现代工业伺服领域[1-2]。目前，大多数的工业自动化现场仍采用比例-积分-微分(以下简称PID)控制器，PID控制器算法简单，通过系统参考值与输出值的偏差，按照比例、积分、微分3个环节构成控制量来达到对被控对象的控制。其中，比例环节参数kp将偏差信号放大或缩小一定倍数，来减小偏差；积分环节参数kI不断积累偏差，来消除静态误差；微分环节参数kD反映偏差信号的变化方向以提前调整输出[3]。传统的PID参数整定大多采用人工手动调节，对于复杂的工业环境，在负载波动大且对速度的精度要求比较高的情况下，传统PID控制器难以达到较好的控制效果。

文献[4]提出一种基于专家思想的PID控制算法，能够有效减小系统的超调量及稳态误差，但专家系统主要用于解决专门的或者比较困难的问题，由于知识面较窄、缺乏自学能力等原因导致其在工程中应用并不多。文献[5]利用模糊控制器调节PI参数，减小负载扰动，加快了系统速度响应，但模糊变量和模糊规则的确定比较费时。

神经网络拥有强大的自学习、自适应能力，在电机控制领域得到了越来越多的关注，与传统PID控制器相结合，能够较好地改善PID控制器的性能[6]。目前应用较为普遍的神经网络主要是误差反向传播(以下简称BP)神经网络和径向基函数(以下简称RBF)神经网络。文献[7]对比了BP神经网络与RBF神经网络在一些非线性曲线拟合上的性能，BP神经网络对于每一个输入样本要调整网络全部的权值，会造成学习时间较长，可能出现局部极小问题；RBF网络是一种局部逼近网络，只有部分权值影响网络输出，提高了训练速度，并且可以有效避免陷入局部极小值。

本文将RBF神经网络应用在PID的参数调整上，为了更好地实现网络输出逼近对象的实际输出，采用梯度下降法沿RBF神经网络性能指标函数的负梯度方向修正网络参数，使网络输出与实际输出的偏差降到最小，通过RBF神经网络辨识获得对象的雅克比(Jacobian)信息，自适应调整PID的3个参数kP，kI，kD，并在积分项采用变速积分以提高控制精度，来满足对PMSM系统的高性能控制要求。

1 PMSM数学模型

PMSM在d-q同步旋转坐标系下的定子绕组电压方程如下：

(1)

磁链方程如下：

(2)

转矩方程如下：

Te=p(ψdiq-ψqid)

(3)

将式(2)代入式(3)可得：

Te=p[ψfiq+(Ld-Lq)idiq]

(4)

当控制d轴电流为0时，可以得到：

Te=pψfiq

(5)

机械运动方程：

(6)

在式(1)～式(6)中，Rs为电机定子电阻；ud,uq为电压d,q轴分量；id,iq为电流d,q轴分量；Ld,Lq为直轴、交轴同步电感；ψd,ψq为d,q轴磁链；ψf为永磁体磁通；p为转子极对数；ω为转子电角速度；Te为电磁转矩；TL为负载转矩；J为转子转动惯量；B为摩擦系数。

2 RBF神经网络模型

RBF神经网络有3层网络，其中输入层与隐含层之间没有权值连接，可以直接把输入向量传到隐含层，对隐含层的输出结果进行线性加权求和，即可得到RBF神经网络的输出[10]。RBF神经网络结构如图1所示。

图1 RBF神经网络结构

图1中，x=[x1，x2，x3]T为输入层的输入向量，h=[h1，h2，…，hm]T为隐含层径向基向量，其中元素hj为高斯基函数，m为隐含层节点数。

(7)

式中：‖*‖为欧几里得范数；cj=[cj1，cj2，cj3]T为第j个隐节点的中心矢量；bj为第j个隐节点的宽度；ω=[ω1，ω2，…，ωm]T为输出层权值向量。

辨识网络的输出：

(8)

辨识器的性能指标函数：

(9)

为实现最优的PID参数整定，RBF神经网络参数的修正应沿着负梯度下降的方向，使性能指标函数最小。

权值更新：

(10)

隐含层中心更新：

(11)

基宽参数更新：

(12)

式中：η∈(0,1)为学习速率；α∈(0,1)为动量因子。

3 基于RBF神经网络的PID整定

基于RBF神经网络的PID自适应控制结构框图如图2所示。

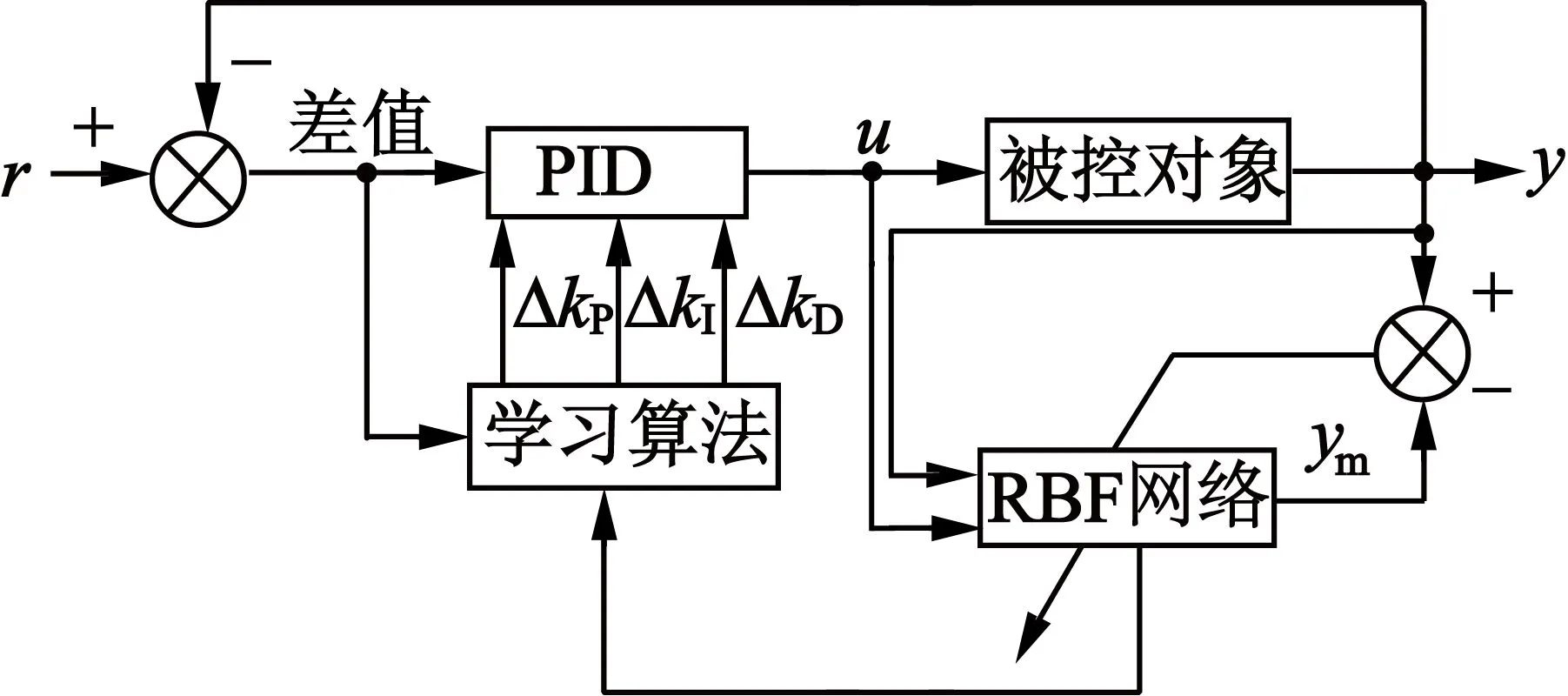
图2 RBF-PID自适应控制结构框图

本文采用增量式PID 控制算法，其控制误差：

e(k)=r-y(k)

(13)

式中：r为参考值；y(k)为系统实际输出值。

PID控制器的3个输入：

(14)

增量式PID控制器的输出：

Δiq(k)=kP[e(k)-e(k-1)]+kIe(k)+

kD[e(k)-2e(k-1)+e(k-2)]

(15)

性能指标函数：

(16)

采用梯度下降法就可以得到kP,kI,kD的调整量，而调整量分别：

(17)

其中，雅克比矩阵(Jacobian)算法：

(18)

4 基于变速积分的积分项的改进

在传统PID控制算法中，加入积分环节是为了增强系统的稳定性，消除静差。但电机在开始起动或者突加负载速度突变的情况下，系统的输出值与参考值之间存在较大的偏差。由式(15)可以看出，这种情况会导致PID的积分项过多累加，可能会使控制量的输出超出所允许的范围，导致系统的超调量较大，甚至会引起系统的振荡[11]。为了提高积分环节的运算精度，当系统出现偏差较大的情况时，应减缓积分项的累加速度，减弱积分环节的作用；反之，积分环节作用应增强。

本文对于PID控制算法积分项的改进是：根据变速积分的原理，使积分环节的累加速度跟随系统的偏差大小自适应变化。系统偏差较大时，积分项可固定在一个较小的值，使积分作用相对弱一些；系统偏差较小时，积分项由RBF神经网络自适应控制。其算法可描述：

(19)

式中：k0为积分项的初始值；a为根据控制对象设定的阈值。

5 仿真分析

本文在MATLAB软件环境下，编写S函数并利用单位延时(Unit Delay)模块建立RBF神经网络PID控制器的仿真模型，其框图如图3所示。

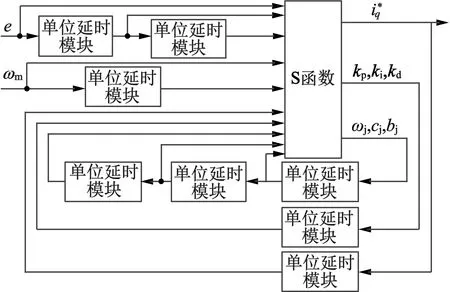
图3 基于S函数的RBF-PID控制器

基于RBF神经网络PID控制的PMSM控制系统框图如图4所示。

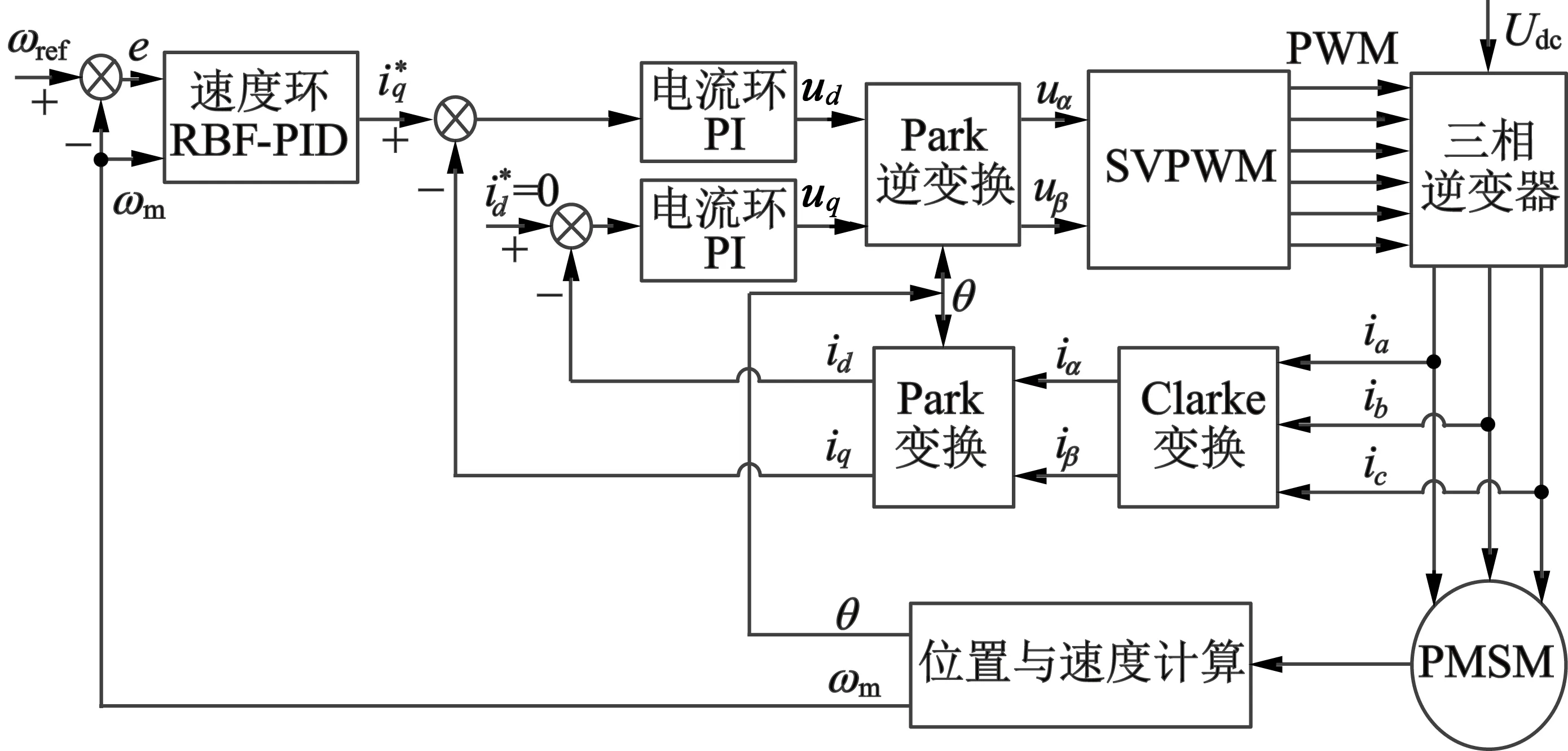
图4 基于RBF神经网络PID控制的PMSM控制系统

仿真所用电机的表贴式PMSM，其具体参数如下：定子电感Ld=Lq=5.25 mH，定子电阻Rs=0.958 Ω，永磁体磁通ψf=0.182 7 Wb，极对数p=4，转动惯量J=0.003 kg·m2。

仿真时PMSM空载起动，给定转速1 000 r/min，0.1 s时负载突变为10 N·m，传统PID控制器和RBF神经网络PID控制器的PMSM转速跟踪控制仿真结果如图5和图6所示。

图5 传统PID控制转速响应曲线

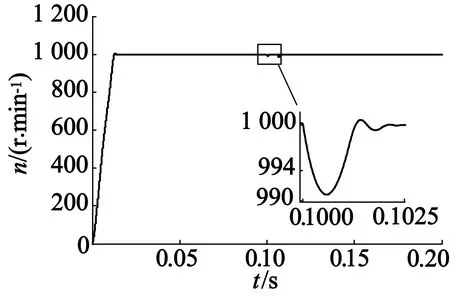
图6 RBF神经网络PID控制转速响应曲线

从图5和图6分别可以看出，空载起动时，在基于传统PID控制的转速响应曲线中，转速超调量为3.23%，调节时间为0.025 s；基于RBF神经网络PID控制下转速响应曲线超调量几乎为零，调节时间为0.014 s。在0.1 s负载突变的情况下，基于传统PID控制的转速响应曲线中，最大转速波动为31 r/min，稳定转速需要的调节时间为0.008 s；而基于RBF神经网络PID控制下的转速响应曲线的最大转速波动为8.5 r/min，稳定转速需要的调节时间为0.002 5 s。由此可见，采用RBF神经网络PID控制与传统PID控制相比，具有更快的转速响应，超调量更小，且负载突变引起的电机转速下降更小，具有较好的鲁棒性。

6 结 语

本文研究了基于RBF神经网络的PMSM的PID控制，利用神经网络的自学习能力来修正RBF神经网络参数，实现了对PID参数的在线调整，解决了传统PID控制器因参数调节困难而无法满足PMSM控制系统高性能调速的问题。通过仿真分析，本文的控制方法弥补了传统PID控制的不足，电机起动稳定，基本无超调，转速响应更快，突加负载后具有更好的抗干扰效果。