高速电机定转子小间隙强迫风冷却数值模拟

程文杰, 李 维, 钟 斌, 肖 玲, 樊红卫, 李 明

(西安科技大学，西安 710054)

0 引 言

现代电机设计紧凑，转矩密度大，并且经常需要承受极端服役环境和负载条件。明确电机内空气流动规律是设计中非常重要的一环，特别是定转子小间隙的对流散热[1]。定转子小间隙内流体的流动可以归结为Taylor-Couette流动(两个同心旋转的圆筒及其之间的流体流动)。这种流动的流动模态随着圆筒转速的升高会不断转变，最终趋于不稳定[2-4]。若再引入轴向流，则此种流动被成为Taylor-Couette-Poiseuille流动[5]。引入轴向冷却流时，定转子间隙内空气的流动即属于这种情形。Hayase[6]对Taylor-Couette流的对流换热进行了数值研究，在他们的模型中，内圆筒的外表面和外圆筒的内表面均匀分布着空腔，计算表明空腔能加强散热。Gardiner和Sabersky[7]测量了Taylor-Couette-Poiseuille流的散热，在他们的实验中有2种结构的转子:1种外表面光滑；1种带有30个轴向槽，结果显示，带槽转子的换热系数明显比前者高很多，并且当轴向雷诺数增加时，泰勒涡的运动衰退了。值得注意的是，上述实验中的泰勒数和轴向雷诺数都较小，另外，在转子表面开槽或者加棒以增强高速永磁同步电机转子的散热尚待进一步研究。Maunu Kuosa[8]进行了高速感应电机强迫空冷实验，转子转速在10 000～80 000 r/min，转子直径71 mm，长度200 mm，轴向冷却流量20～60 g/s，获得了摩擦系数、速度因子以及对流换热系数，并且和数值仿真(定子和转子表面给定恒温边界条件，并且定转子均具有光滑表面)结果进行了对比。在其后的研究中又获得了转速5 000～40 000 r/min，轴向冷却时，槽开口封闭/不封闭的定子和表面光滑/开槽转子4种组合情形下的对流换热系数[9]。需要指出的是，对流换热系数的值与换热过程中流体的物理性质、换热表面的形状、部位、流速以及表面粗糙度相关。它只是一个经验系数，适用于模型相同或近似的散热问题，如果模型变化，此值也会变化。如果将特定环境下的实验结果推广到其它场合，则有可能会出现问题。这种实验研究的特定性已经一次又一次被人们证实[10]。由此，针对特定机组的冷却进行数值计算和实验研究是必不可少的。

工程中可采用定子槽并联定转子环形间隙的方法来增加冷却流量，文献[11-13]研究了这种并联冷却方案的风摩擦损耗。文献[14]利用对流换热系数半经验公式进行了永磁电机的热设计。而目前鲜有关于这种并联冷却方案的散热效果及其局部对流换热系数的研究。因此，本文以一台2极3相，额定功率10 kW，120 000 r/min的超高速永磁同步电机为例，对各种工况下的电机定转子小间隙强迫风冷进行有限元数值分析。

1 三维模型及边界条件

根据旋转周期性对称，取电机结构的1/12进行分析，考虑到定子线圈所占的空间，简化的定转子间的间隙模型如图1所示。

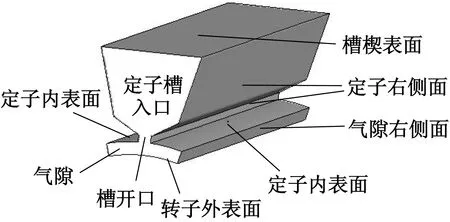
图1 电机流场计算流体力学(CFD)模型

此间隙模型为转子冷却空气流道，由定转子环形间隙、定子槽开口和定子槽3部分组成。电机在正常运转时内部气体流动可看作是定常流动，因此可忽略流动控制方程中的时间相关项。为简化计算，作如下假设：气体是不可压缩的；轴向流垂直于气隙入口截面流入；在传热效应上，转子等效成薄壁筒；不考虑定子损耗的影响，即定子槽的所有壁面视为绝热；转子的损耗用其表面的热流密度来刻画。

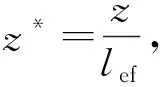
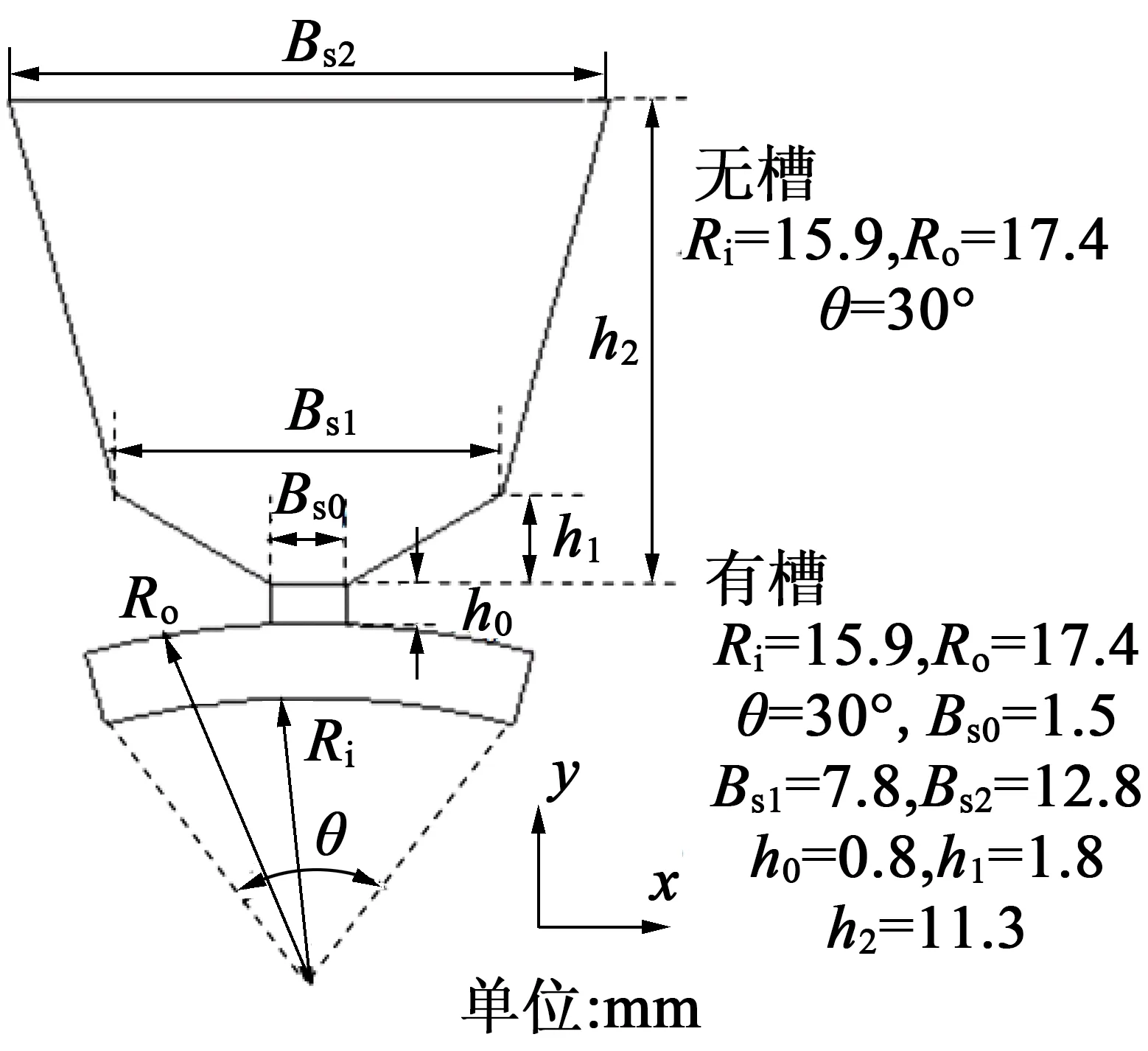
图2 模型横截面及尺寸

转子的实际横截面如图3所示，转子外层为保护套，材料为高温镍铬合金，内层为实心永磁体，材料为钐钴。为了缩减计算时间，可以根据能量守恒定律，将转子等效为厚度δ的薄壁圆筒。薄壁圆筒的等效密度ρcylinder和等效比热容Ccylinder按下式计算：

图3 热计算时电机转子的等效

(1)

(2)

式中：角标PM，sleeve分别表示永磁体和保护套的参数。

2 转子表面应力场及风摩擦损耗

转子在高速旋转过程中，定转子之间的气体处于湍流状态，会产生湍流应力(亦称雷诺应力)，并且在大多数情况下，湍流应力比分子黏性应力大的多[15]。于是转子需要克服其表面的气体湍流剪切应力做功，表现出风摩擦损耗的特性。风摩擦损耗的功率：

pw=SrotorτRiω

(3)

式中：Srotor为转子磁钢段表面积；τ为转子表面剪切应力；Ri为转子外半径；ω为转子角速度。

2.1 定子无槽和无轴向流

当算例为无槽无轴向流时，转子表面的剪切应力沿轴向分布如图4所示。

图4 无槽无轴流时转子表面剪切应力分布

图4中，转子表面的剪切应力是沿轴向呈波浪状分布的，而且随着转速的增大，剪切应力增大。值得注意的是，转速升高时，单位长度内剪切应力波峰的个数减少了，即波长变长了。图5为子午面r-z平面上的径向和轴向速度矢量图，两者的矢量之和形成泰勒涡。

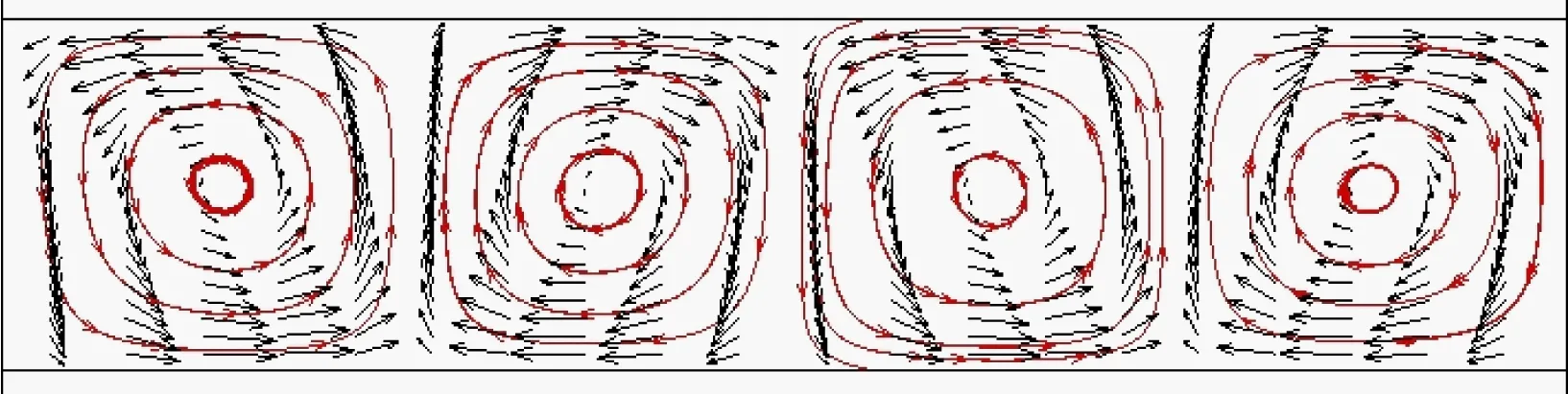
图5 r-z子午面上的泰勒涡

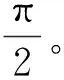
图6 无槽无轴向流120 kr/min下转子表面剪切应力场与速度

当定转子间隙通入轴向冷却空气时，气隙内的损耗包含摩擦损耗和流动损耗2部分。其中，摩擦损耗由转子旋转引起；流动损耗与进入气隙内的冷却流被周向加速相关，风摩擦损耗的经验计算公式见文献[16]。如图7所示，有限元解与Bilgen的模型计算结果吻合，与Yamada模型计算结果有较大差别，原因可能是有限元模型中的转子表面粗糙度与经验模型中的粗糙度系数之间的差别。

图7 定子无槽无轴向流时风摩擦损耗对比

2.2 定子槽和轴向流对流

2.2.1 定子开槽无轴向流

定子开槽无轴向流时，远离槽开口转子表面的剪切应力沿轴向分布如图8所示。可以看出，定子开槽后的转子表面剪切应力随转速的升高而增大，但沿轴向分布波动非常小，几乎是一条直线。而且相同转速下，开槽后的转子表面剪切应力要比无槽时大(120 kr/min时较无槽的大30%)，随着转速的增大，风摩擦损耗增速变大。

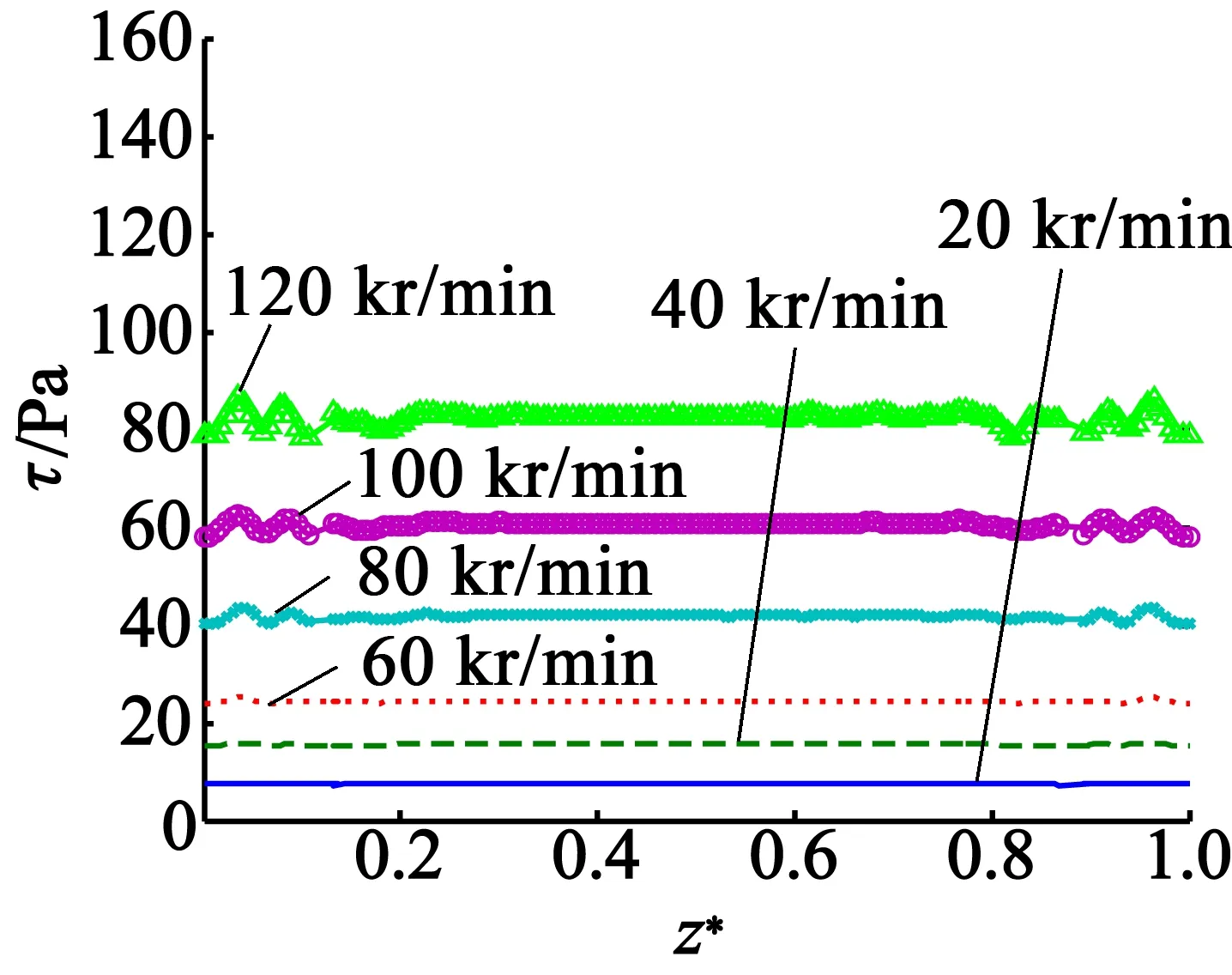
图8 转子表面剪切应力分布(120 kr/min,有槽无轴向流)

当转速为120 kr/min时，将图8中剪切应力场与气隙中部的速度场进行对比，如图9所示。由图9可见，径向速度与轴向速度都非常小，接近于0，气流总速度主要体现为周向速度，并且总速度小幅波动时，应力也随之波动。具体表现：总速度减小时，应力增大；反之亦然。这说明，当气流速度升高时，转子对气流做功减小(表面剪切应力减小)，气流速度便降下来；当气流速度降低时，转子对气流做功增大(表面剪切应力增大)，使气流速度升上去，从而实现一种动态平衡。

图9 120 kr/min下转子表面剪切应力场与速度场对比

如图10所示，有槽无轴向流模型有限元解与Bilgen模型结果吻合。这一方面证明了有限元求解的正确性；另一方面给出了有限元参数与经验公式参数之间的对应关系。

2.2.2 定子开槽有轴向流

如果考虑转子外表面的强迫风冷，则需要进行有槽有轴向流模型的计算。

图11为3种计算模型(无槽无轴向流，有槽无轴向流，有槽有轴向流)，在120 kr/min下的转子表面剪切应力沿轴向分布的情形。其中，无槽无轴向流时，应力呈正弦波动；有槽无轴向流时，近似为一条直线，且平均值要比无槽无轴向流时大33.3%；有槽有轴向流时(40 m/s轴向风速)，从入口端至出口端，应力逐渐减小，且平均值在3种计算模型中最大，约为无槽无轴向流时的1倍。当引入轴向流后，原先只具有轴向速度的气流进入到定转子间隙后，在圆周方向上被加速，所消耗的能量由转子提供，故在入口段转子表面剪切应力最大；沿着轴向，气流的圆周速度越来越大，经过一段距离后，圆周速度稳定下来，从此处开始，转子表面剪切应力稳定，与无轴向流时情形类似。

图11 3种计算模型下的剪切应力对比(120 kr/min)

3 转子表面温度场及对流换热系数

文献[16]给出了高速电机的对流换热系数h的半经验计算公式：

(4)

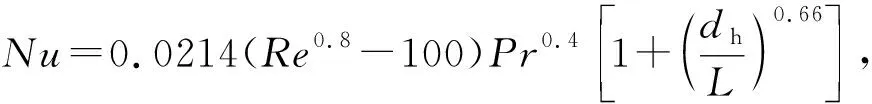
本文考虑了转子无热源和有热源2种情形。转子无热源相当于转子只有风摩擦损耗，无其它体热源；转子无热源是在前者基础上加上了涡流损耗。当定子开槽，转速120 kr/min，轴向风速40 m/s，无热源时，转子表面温度从入口至出口逐渐变大，最高温度在出口处，约为60 ℃。有热源时，出口处最高温度约85 ℃，对流换热系数从入口450 W/(m2·K)至出口150 W/(m2·K)逐渐减小，平均值约为300 W/(m2·K)，如图12所示。

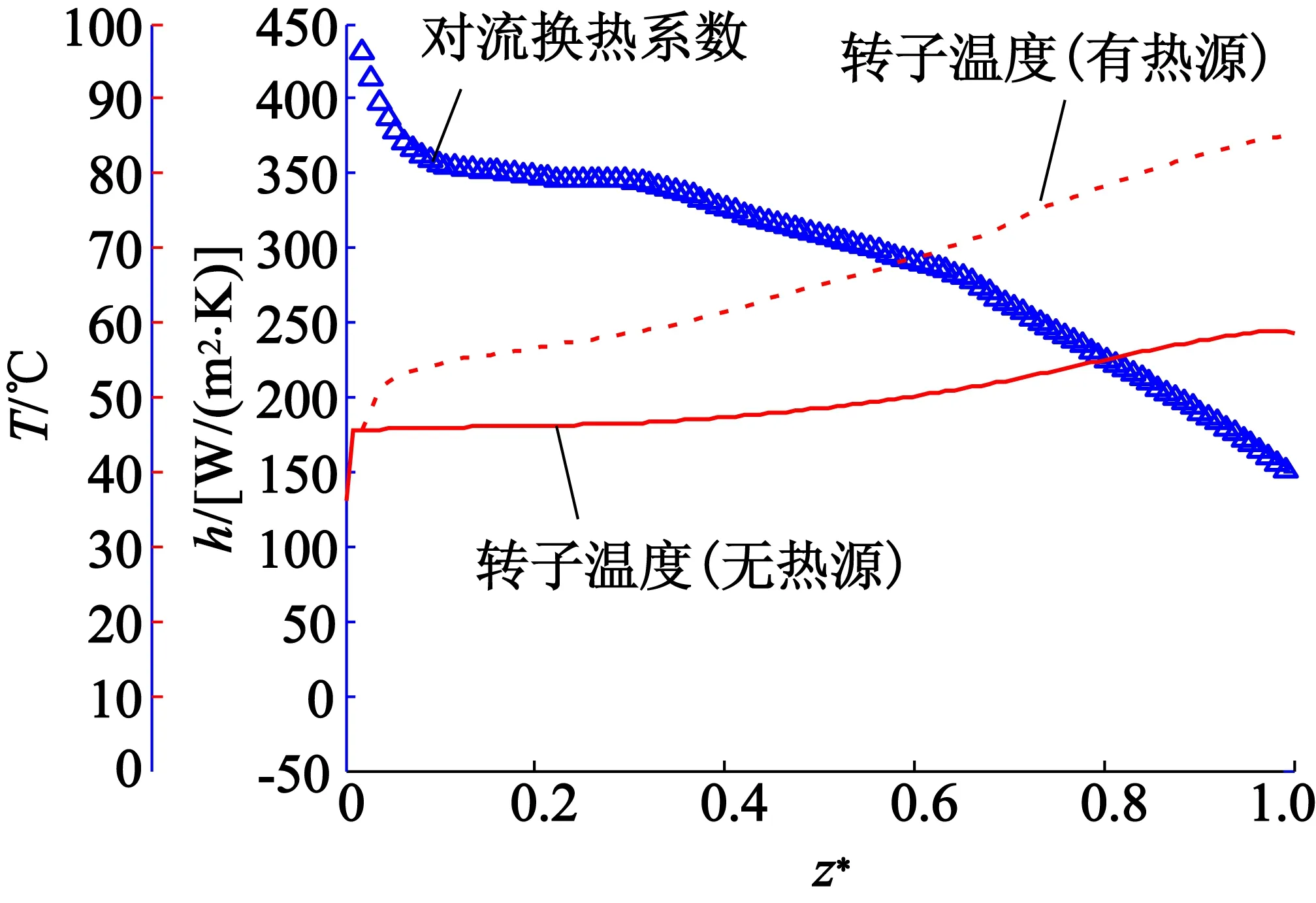
图12 转子温度场和局部对流换热系数

图13显示了r-z平面上的轴向流场。入口端的轴向流速均为40 m/s，出口端的轴向流速在定子槽底部约为45m/s，而在定转子环形间隙内约为10 m/s。由于定转子环形间隙窄，流阻大，所以环形间隙内的气流轴向速度会小于定子槽内的轴向速度；另外又由于转子旋转的离心作用，环形间隙内的气流会有一部分进入到定子槽中，导致转子表面的冷却气量减小。以上2种因素是转子表面对流换热系数沿轴向不断减小的主要原因。

(a) 偏离对称纵截面7°的面

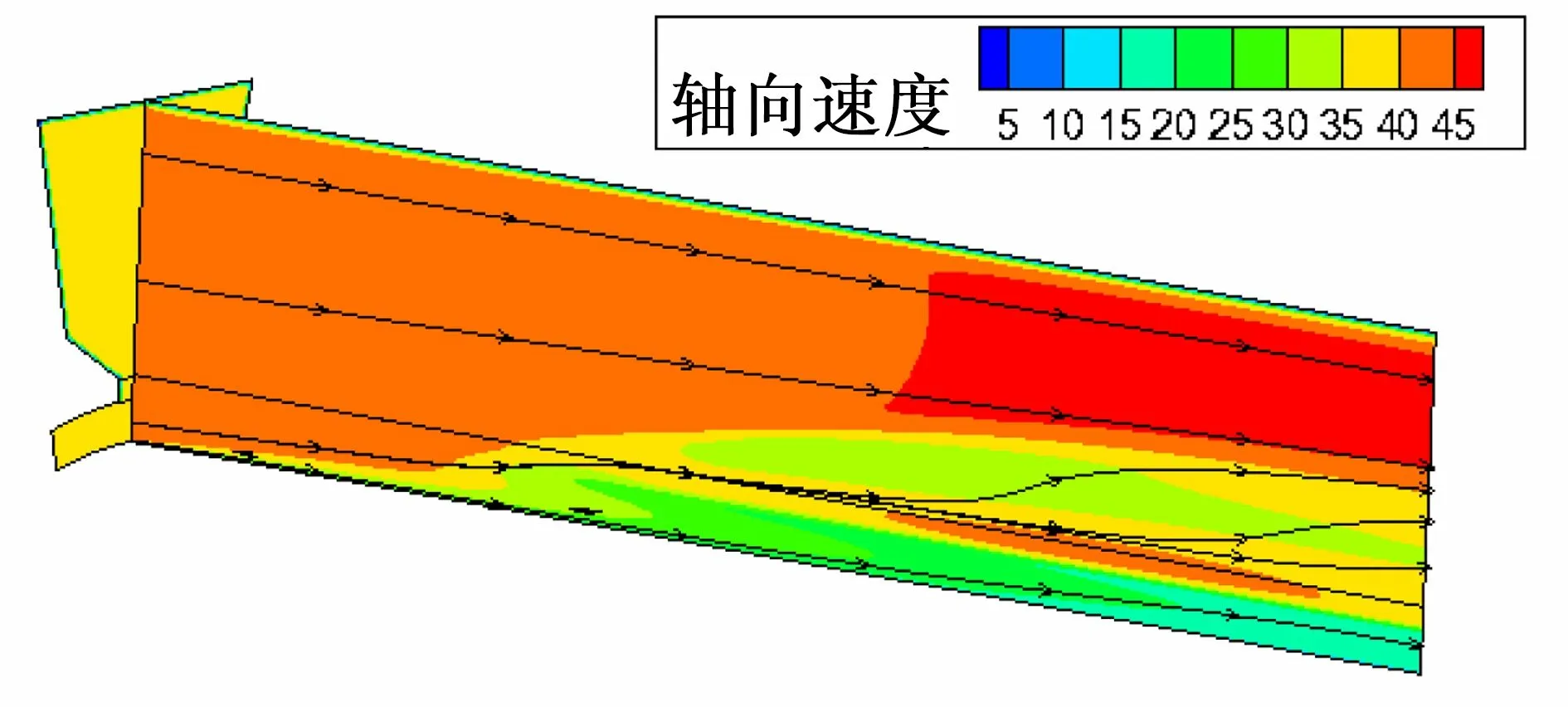
(b) 对称纵截面

当定子开槽，转子有热源(138 W恒定热源)时，对比了不同转速，不同轴向流速下的平均对流换热系数和转子最高温度，如图14所示。

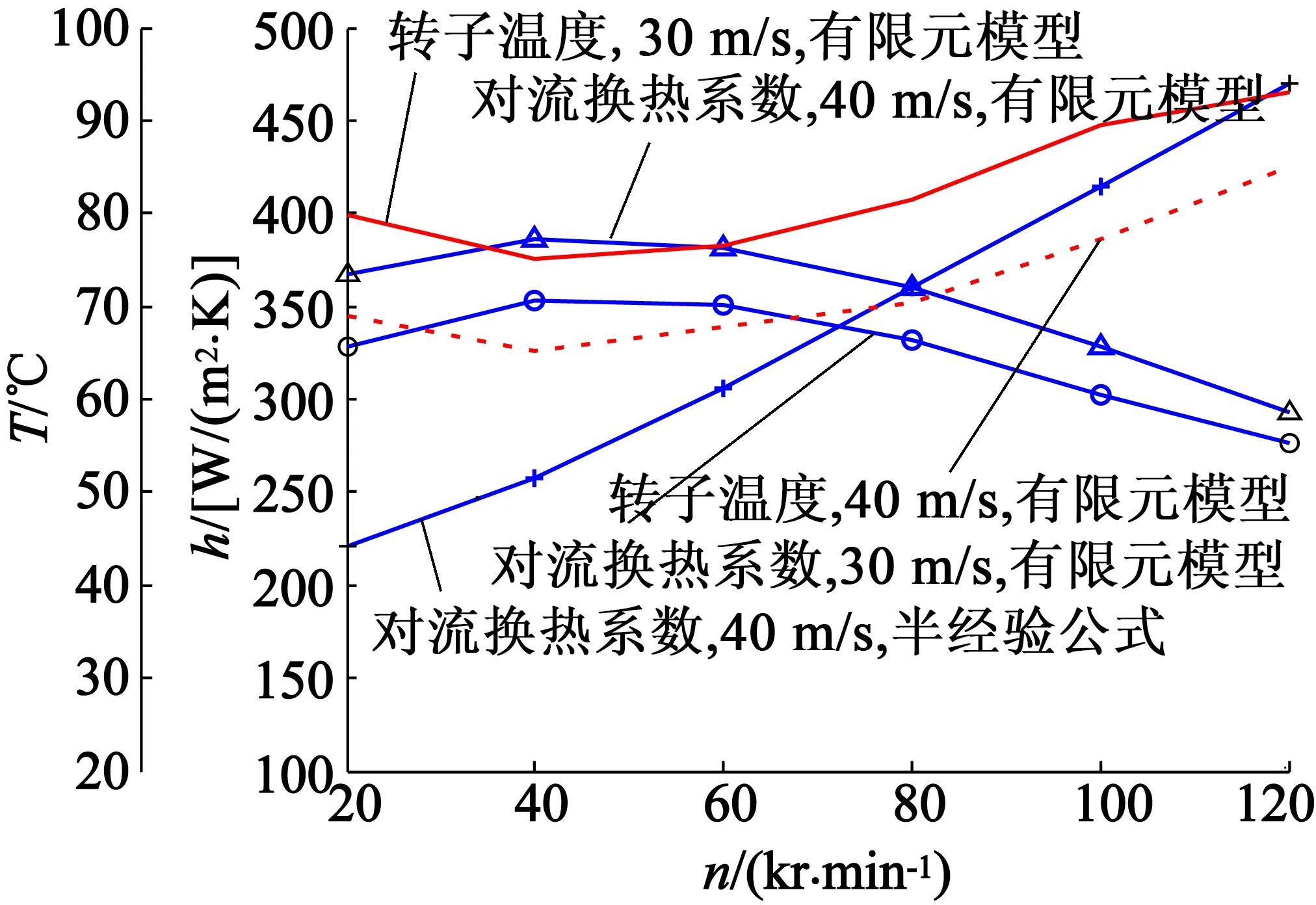
图14 不同冷却条件的平均对流换热系数和转子温度

由图14可见，相同转速下，轴向风速越大，转子最高温度越低。当轴向风速固定时，转子最高温度随转速先降低后升高，对于本例，对于30～40 m/s的轴向风速，转速在40 kr/min左右转子温度最低。其原因为：当转速小于40 kr/min时，风摩擦损耗小，定子开槽会增强定转子环形间隙与定子槽之间空气的对流，有利于散热；当转速大于60 kr/min，风摩擦损耗随转速增大而急剧增大，恶化了散热条件。另外，当轴向风速固定时，转子对流换热系数随转速的增加先变大后减小，这一现象与文献[9]的结果是一致的。对于本例，当轴向风速为30～40 m/s时，对流换热系数在转速40 kr/min左右最大，散热效率最高。

以上说明对于一个特定的轴向风速，存在一个特定的转速，使得在这种情形下转子的温度最低。虽然，引入轴向流会增加一部分转子的损耗，但从实例计算中发现，轴向流的冷却效果远远胜过其造成的损耗发热效果。根据对流换热半经验公式式(4)计算出的转子平均对流换热系数随转速增大而增大，半经验公式解与有限元解在80 kr/min吻合，在其它转速范围内存在一定差异，两者之差最大值约为150 W/(m2·K)。这可能归结为以下原因：半经验公式没有考虑槽效应，而且只适用于描述管道内充分发展的流体，而有限元模型中有定子槽，而且定子轴向长度较短，气隙内的气流还处于发展阶段。

当定子开槽且无轴向流时，可以用等效热导率法[17]来描述定转子小间隙的对流散热。该方法的原理是：如果单位时间内静止流体在定转子之间所传递的热量和流动空气所传递的热量相等，那么可以将旋转的转子视为静止不动，而只需要修改空气的热导率。通常情况下，定转子环形小间隙内空气的流动为紊流，气隙的有效导热系数可以根据文献[17]计算：

λeff=0.001 9η-2.908 4Re0.461 4ln(3.333 61η)

(5)

当电机只有定子外壳水冷时(定子表面对流换热系数533 W/(m2·K))，设置定转子环形间隙内空气的等效热导率系数，计算结果如图15、图16所示。

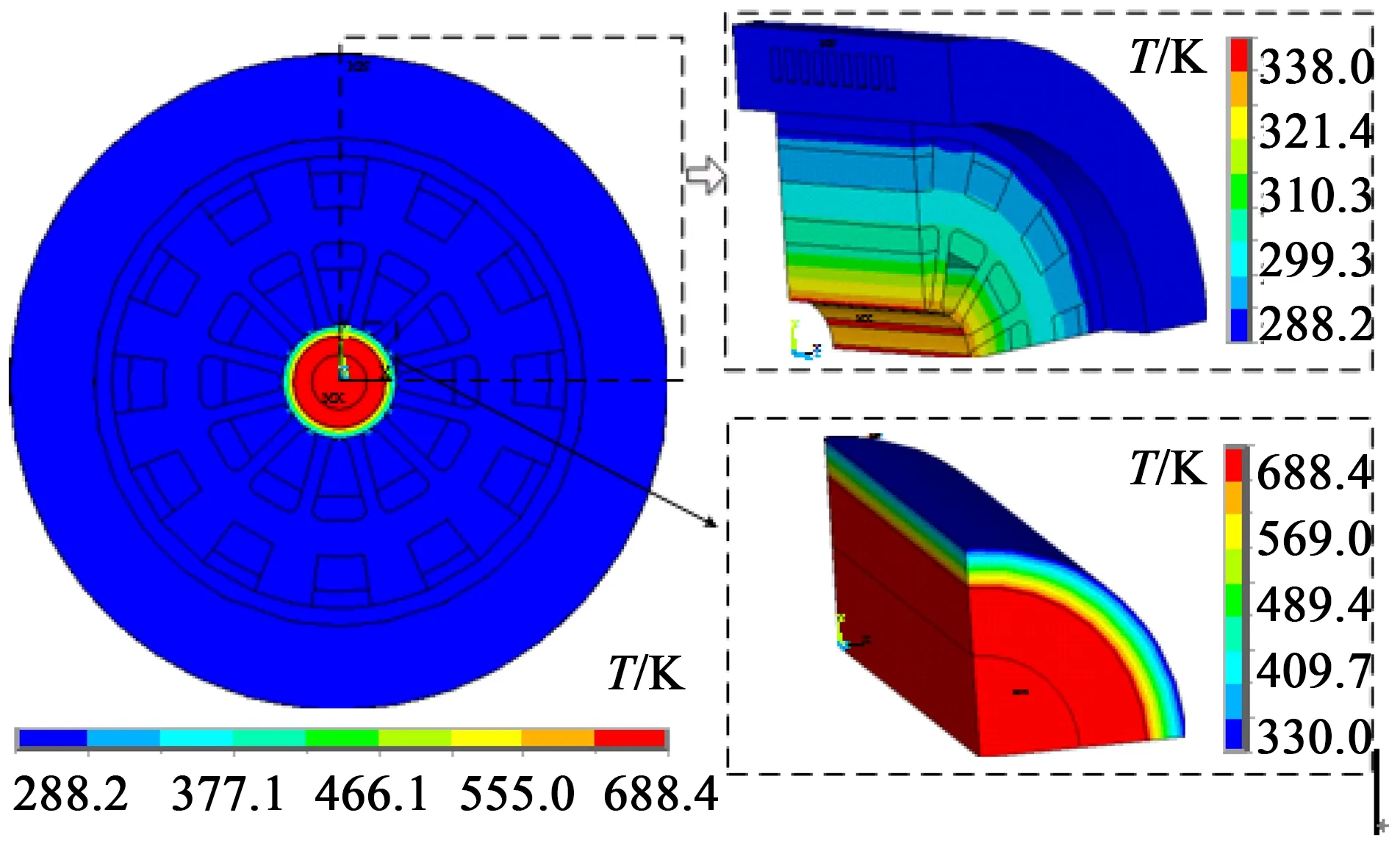
图15 定子外壳水冷750 s时电机的温度场

图16 定子外壳水冷时转子内部温度-时间曲线

图16显示，转子内部温度趋于一个稳定值，说明电机最终会达到热平衡状态，达到热平衡态的时间大约为750s。稳态时，转子最高温度为688K(415 ℃)，已经超过了钐钴永磁体的工作温度(350 ℃)，这说明仅依靠定子外壳水冷来对转子进行散热的方案是不合适的。且气隙中定子内表面处的温度比转子外表面处的高约358 ℃，这说明转子的热量通过这层环形空气传递给了定子硅钢片和定子槽内空气。尽管空气的比热容很大，如表1所示，但是密度非常小，所以环形空气所存储的热量非常小，约为6.3 J。虽然，稳态时环形空气的散热功率与转子的发热功率相等，但是在750 s之前，转子的温度会急剧上升，这由以下2方面的因素引起：由于空气的等效热导率较小，这使得转子的热量较难传递进空气环中，空气环对转子产生了热屏蔽效应；环形空气储热量小，在初始时刻，空气无法更多地吸收转子的热量，从而引起转子温度迅速上升。

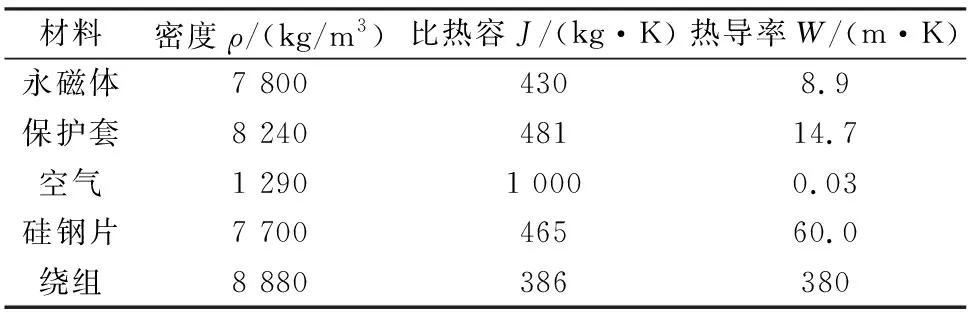
表1 室温下电机材料属性

4 结 语

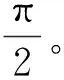
2) 有槽无轴向流时，转子表面剪切应力沿轴向分布波动非常小，几乎是一条直线，意味着泰勒涡消失。相同转速下，开槽后的转子表面剪切应力要比无槽时大，120 kr/min时较无槽无轴向流的大33%。

3) 当轴向流进入到定转子间隙后，在圆周方向上被加速，所需要的能量由转子提供，故转子表面剪切应力在入口段最大，并沿着轴向流速方向逐渐降低。轴向风速40 m/s对应的转子表面剪切应力平均值约为无槽无轴向流时的2倍。

4) 定子开槽，引入轴向流后，转子表面对流换热系数沿轴向不断减小。在相同转速下，轴向风速越大，转子最高温度越低。当转速较小时，风摩擦损耗小，定子开槽会增强定转子环形间隙与定子槽之间空气的对流，有利于散热；但当转速增大到某一值后，风摩擦损耗会急剧增大，恶化散热条件。因此，对于一个特定的轴向风速，将存在一个特定的转速，使得转子散热效率最高。

5) 由于空气的等效热导率较小，使得转子的热量较难传递进空气环中，空气环对转子产生了热屏蔽效应；另外，环形空气储热量小，在初始时刻，空气无法更多地吸收转子的热量，从而导致初始时转子温度急剧上升。