让中考复习课充满探究味*——从一节“尺规作图作平行线”课例谈起

☉福建省厦门五缘实验学校 陈海烽 马光德

探究是学生获得数学知识的重要途径.探究学习对于提高学生的核心素养，尤其对于创新精神与实践能力的培养具有重要意义.因为探究既能满足学生的求知欲和好奇心，又能使学生更有获得感，更能体验到对数学的“深层理解”.探究的过程本身可以使学生的思维受到良好的锻炼，学生需要调用自己的已有知识和经验，有利于学生“温故知新”［1］；学生也需要在探究的过程中合作、解释，有利于培养学生的交流表达技能，这些均指向学生核心素养的提升.

如何上好中考复习课一直是困扰数学教师的一个难题.张奠宙先生曾说过，难见一堂好的复习课.笔者认为其原因有：学生经过了新授课的教学，对知识产生了“喜新厌旧”的心理；通过新课教学学生对知识的认知出现了较大的差异，换句话说，学生已经不在同一个起跑线上.复习课的两大任务是知识巩固和能力提升，如何才能使学生仍然像新授课一样保持好奇心，既起到巩固知识的效果，又能建立知识之间的联系，促进能力的提升？设计好的复习探究是提高复习效益的重要途径.下面结合自己的一节“尺规作图”课，谈谈自己的看法.

一、课堂呈现

师：请大家拿好直尺和圆规，准备做一道题.过点A作直线平行于已知直线l.（如图1）

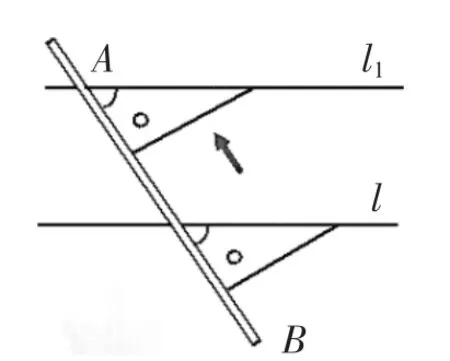
图2

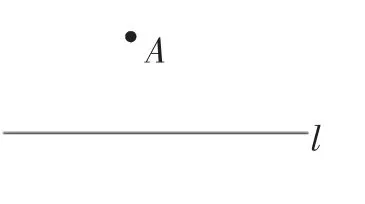
图1

生1：（面露难色）这个题怎么能做呢？题目没有问题吧？

生2：用三角板和直尺平推法作图.

师：（教师展示）像这个同学用直尺和三角板作图（见图2），可以吗？

生3：违背尺规作图的原则.

师：是的，尺规作图只能用无刻度的直尺和圆规这两样作图工具.这个题目本身没有问题，如何作呢？大家再想想.

师：看来大家有点为难.让我们回想一下，我们知道哪些基本作图方法？

生4：作一条线段等于已知线段，作一个角等于已知角，作一条线段的垂直平分线，过一点作一条线段的垂线；作一个角的平分线，作一个图形的轴对称图形，用描点法作函数的图像……

师：大家看看，哪些可以帮助我们做这道题？

生5：作一个角等于已知角.

师：很显然，我们必须找到同位角相等或内错角相等……然后两直线平行.

生6：我会作了.如下（见图3）：作一条直线a与l相交得∠1，然后作一个角等于∠1，则根据同位角或内错角相等，可知这两条直线是平行的.

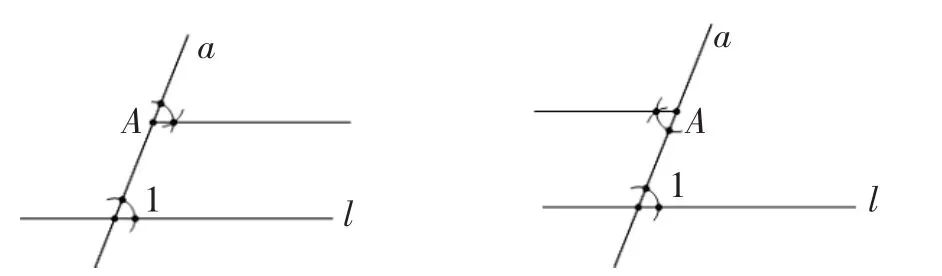
图3

生7：根据生6的作法，如图4，得到∠2，然后作一个角等于∠2，显然有同旁内角互补，两直线平行.

师：以上几个同学做得很好，现在我们的思路打开了，还有没有别的方法呢？这是从一个角等于已知角的方法入手，能否用其他方法？建议同学们用这样的句式来说明，我的作法是_____，原理是_____，涉及的基本作图是_____.

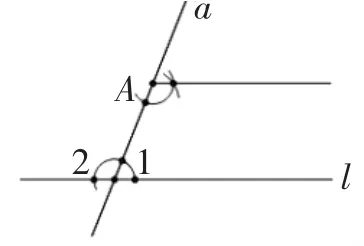
图4

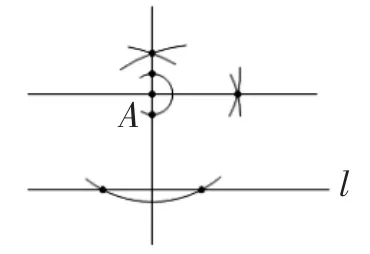
图5

生8：我的作法是：先过点A作l的垂线a，然后过点A作直线a的垂线.原理是：同旁内角互补，两直线平行，或者说：在同一平面内，垂直于同一直线的两直线平行.用到了两次“过一点作已知直线的垂线的基本作图法”.（见图5）

师：妙吗？妙要大声说出来.这位同学打开了思路.从什么方向找的平行？由他的启发，我们可以从结论平行线出发，寻找自己的作法.

生9：我受生8启发，作法：先过点A作a⊥l于点B，然后继续在l上找另外一点C，再过点C作b⊥l，接着量取AB=CD，显然四边形ABCD是矩形，所以AD∥l.原理是：矩形的对边平行.我用到了过一点作一条直线的垂线的方法，还有作一条线段等于已知线段两种基本作图.（见图6）

师：真是个好主意，看到了吗？生9用了两种基本作图，过一点作已知线段的垂线，还有作一条线段等于已知线段.提醒我们什么？可以多种方法配合.

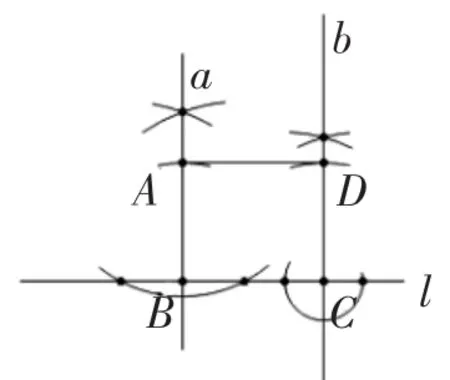
图6

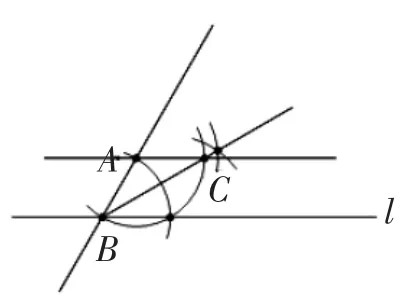
图7

生10：我的作法是：过点A作一条直线与l相交得∠1，然后作∠1的平分线，再截取AB=AC.原理是：角平分线+等腰三角形➨平行线.用到两个基本作图：作一个角的平分线和作一条线段等于已知线段.（见图7）

生11：（鼓掌）当然也可以在另外一侧作！我还有一种作法.作法是：以AB为边作一个菱形.原理是：菱形的对边平行，比他更简单些.用到一个基本作图：作一条线段等于已知线段，只不过用了三次.（见图8）

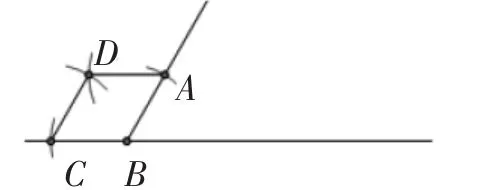
图8

图9

生12：显然可以更一般化些，就是作一个平行四边形.原理是平行四边形的对边平行.也是用了作一条线段等于已知线段，但两次取的线段长度不必一样.（见图9）

师：（欣赏地看着学生）思路一旦打开，谁都拦不住.好了，有这么多种方法，能否总结整理一下？对我们今后寻找解题办法有何启示？大家分组讨论一下，然后请各小组派代表展示.

小组1展示：我们小组将讲过的方法整理了一遍，这样很直观.（见表1）

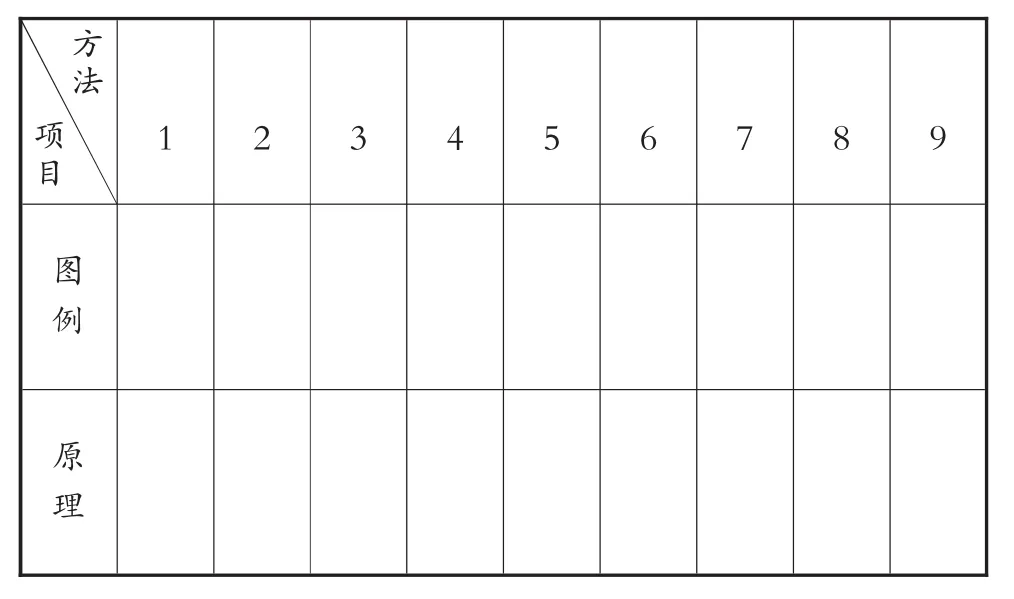
表1

师：表格有很好的直观性，是收集和整理信息的一个重要工具，大家可以向小组1学习.

小组2展示：我们组觉得这道题看起来好像是尺规作图的方法，其实实质是寻找证明平行的方法.所以我们以“平行”为核心，整理出如下思维导图.这样我们作图的各种原理就很清晰了.（见图10）

图10

生13：通过整理这个知识，我发现还有一种方法.作法：过点A作直线a与l相交于点B，延长BA到B′，使AB=AB′，再过点B′作直线b交l于点C，然后作线段B′C的中垂线得B′C的中点D，则有AD∥l.原理是：三角形的中位线平行于第三边.用到两个基本作图，分别是作一条线段等于已知线段和作一条线段的垂直平分线.（见图11）

生（众）：妙呀！

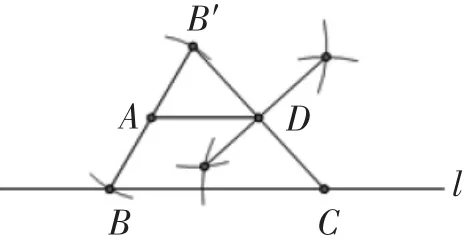
图11

师：很好，生13抓住了问题的核心，就是平行.这道题本质上就是证明平行的各种办法.小组2还涉及一种办法.什么方法？它能帮我们作图吗？

生（众）：平行于同一直线的两直线平行.这个需要化归为在两直线平行的基础上，显然方法不妥.

师：很好，用了一个很妙的词语——化归，这也是数学的灵魂.

小组3展示：我们组从解题坐标系入手，将作图的方法作为方法轴，将学过的数学知识作为知识轴，建立如下所示的坐标系，如图12所示：

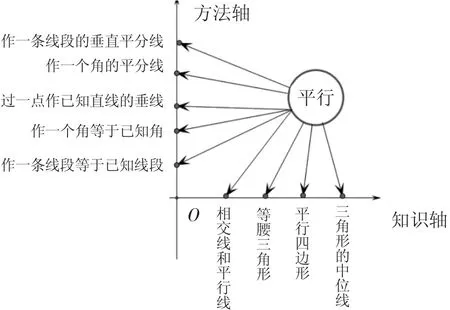
图12

师：小组3的同学富有创意，看来我们之前的解题坐标系运用得很好.这样就像是一张知识地图，很好地将题目的知识和方法有序地展示了出来.然后分别往两坐标轴进行投影，使得整个知识与方法联系十分紧密.三组同学的代表都阐述得很好，大家看看哪种更值得学习？

生：支持第三种——解题坐标系，很有数学味道.

师：第三种整理办法就像是一张知识地图，更有利于后续的学习，它还蕴藏着大能量，可以解决更广的问题.从本节课我们可以看出，同学们通过认真探究，思考问题时能抓住关键的核心——平行，从这个目标寻找可行性办法，将一个陌生的问题转化为熟悉的问题.我想大家肯定会有不同程度的收获.特别是整理探究这个环节，相当于围棋的复盘，就是将自己的和朋友的作法再次做个梳理，这样我们今后探究类似的问题时有经验可循.

二、教学思考

1.复习探究课要精心设计复习题材，激活学生的探究欲望

在复习中，找到一个好的复习题材往往能使复习事半功倍.本案例中，笔者提供一道尺规作图题让学生探究.过直线外一点作平行线，这个内容在新授课时我们就是用平推法作出来的，但是它不属于尺规作图.这个问题接近学生的最近发展区，但要经过一定的思考.正如上课伊始许多学生并没有一下子就反应过来.经过笔者的引导，学生的探究欲望被激发了出来，从而使探究的方法井喷.一个好的题材，就像颗石头一般投入平静的湖面，会引发阵阵涟漪.因此，教师在复习时要多琢磨复习题材的选择.例如，对于中考函数的复习，我们可以设计一个题材，探究y=x+的性质，让学生通过已经学过的研究函数的一般方法研究这个函数的定义域、值域、单调性、对称性、奇偶性、最值，核心是通过图像研究，可以让学生描图，然后逐步感知，进而一步一步探究，直至完整地揭示这个函数的性质.换句话说，让学生将研究函数的程序走一遍，这样研究初等函数的方法就得以巩固并有新的认识，乃至今后遇到一个陌生的函数时也能泰然处之.总之，数学探究课内容的选择是完成探究性学习的关键.选择的教学内容要有助于学生对数学的理解，有助于学生体验数学研究的过程，有助于学生形成发现、探究问题的意识，有助于鼓励学生发挥自己的想象力和创造力，因此，探究课题的内容要具有开放性，围绕课题学习的预备知识不要走出现有的数学知识的范围.

2.复习探究课要动手实验整理反思，丰富学生的探究手段

复习需要做题，但不能仅仅是做题，学生在复习中不断地刷题容易产生厌倦.应充分调动学生的各种感官参与复习，使学生自然地卷入复习过程，积累相应的探究经验，动手实验是一种很好的选择.在动手中，学生的焦虑感降低，认知负荷减少.本案例中，学生通过自己操作直尺和圆规，在自己思维活动的参与下，将过直线外一点作平行线的方法探究得异彩纷呈.同时本案例中学生利用表格和图像的直观性，开发出相应的整理知识的方法，也促进了知识的内化提升，进而提高学生的数学核心素养.

3.复习探究课要多点期待多点空间，延展学生的探究过程

在学生的探究过程中，教师要充分发挥学生的主体作用.教师退一步，学生进十步.相信学生的潜能，多给学生一点时间和空间.教育要有农人精神，要懂得守望.本课例中，笔者除了在开头学生遇到困难时进行提醒，其他都是由学生自己探索，可以欣喜地看到，学生在回答问题时说受到了哪位同学的启发，这表现出学生有良好的倾听能力，有助于学生之间互相学习、互相欣赏，可培养良好的合作探究的品质.在完成画法之后，我只是引导学生整理知识，让他们进行小组合作，去分享，结果，我们看到了三组非常有代表性的成果，使得本课学习的价值得到了质的提升.

4.复习探究课要创设结构信息关联，提升学生的探究层次

在复习中，将数学知识建立一个系统是提高复习效益的一个重要方法，它就是华罗庚先生所说的将书读薄的举措之一，也是锻炼学生概括思维的重要方式.本课例表面上是让学生复习尺规作图的方法，更核心的知识是让学生掌握平行的各种判定方法并综合运用.本课例中，学生巧妙地利用表格、思维导图、解题坐标系，对知识进行巧妙连接，有利于培养学生的创造性思维.特别值得一提的是，解题坐标系和许国泰先生的“信息交合理论”极为相似.通过知识轴与方法轴两个维度建立起作图知识与作图方法的关联，提高了探究的自觉性，进而激发学生对探究过程的元认知监控，并加以运用.本课例中，生12提供的最后一种方法，就是在整理知识过程中灵光一现获得的.在知识和方法螺旋上升的过程中，探究的层次不断提升.我们知道，数学探究的教学层次可以分为基础层次、中间层次、较高层次.基础层次是教师或教材给出问题，要给出探究的主要步骤，制定结果的呈现形式，对可能出现的问题给出适当的提示.中间层次是教师或教材给出问题，要给出探究的简要过程和需要的提示，对结果的程序给出大致的要求，可以适当地不加限制.较高层次是教师或教材给出问题，对探究的步骤、结果呈现的形式都不设限定，问题有一定的开放性，给学生提供一个创新的空间［2】.本课例对作图的探究处于中间的层次，笔者为了让学生的表达更加规范并富有逻辑性，对表达的方式作了相应的规范，即先说作法，然后阐明原理，说明涉及了几种相应基本作图.而后半段对作图方法的归纳和总结显然处于较高的层次.笔者对学生的呈现形式不作要求和设定，给予了学生更大的灵活度，让学生发挥自己的主观能动性，最后出现了喜人的效果.

总之，中考复习是老生常谈的教学话题，复习内容不再新鲜，倘若我们能选取一个支点，让学生进行探究，使之能以点带面，连成一片，进而提高复习效益，这非常值得开发、设计、应用和尝试.