坐标测量机测头半径快速补偿方法

王卓然，何小妹

(中国航空工业集团公司北京长城计量测试技术研究所，北京 100095)

0 引言

在航空发动机叶片的测量中，常用坐标测量机来完成叶片型面的测量［1］。叶片型面测量的实质是对复杂曲面的测量，在测量过程中采用矢量化测量，即沿着法矢方向进行接触式测量。坐标机得到的叶片点云对应测头球心的坐标，但与实际需要的接触点坐标之间存在误差。该误差的引入对后续拟合等数据处理存在影响。因此，需要进行测头半径补偿，以抵消实际轨迹与测量轨迹之间的差异。

目前，坐标测量机广泛采用一种二维在线自动补偿方法，即在测量时，将测量点和测头半径的关系都简单处理成存在偏移，从而自动完成数据的测头半径补偿［2］。对一些由规则形状组成的表面的测量，如平面等，该补偿方法是准确的。但对于复杂曲面，如发动机叶片曲面，测量方向和测量点的法矢有可能不一致，用此补偿方法进行补偿会造成补偿误差［3］。另外，还可根据已知的解析函数表达式，利用对函数表达式求导数，得出各测量点处的法向矢量［4］。但是由于在实际叶片测量中，叶片曲面较为复杂，且函数表达式多数为未知量，所以此方法并不适用于叶片测量中的测头半径补偿［5］。

为了弥补现有方法存在的计算过程繁琐、效率低下的缺点，并解决在复杂曲面补偿中存在的内部程序处理时间较长和补偿精度不理想等问题，本文在现有算法的基础上，提出了一种快速测头半径补偿算法。该算法能够在保证补偿精度的情况下，最大限度地提升计算效率，从而更高效地应用于实际测量中。

1 测头半径的引入误差

为分析测头半径补偿原理，首先阐述测头半径引入误差的原因。在测量叶片时得到的球心轨迹与叶片曲面的表面距离为测头半径。测量过程中，球心与接触面轨迹如图1所示。测头与被测叶片曲面接触时，球心在被测点的法线上，而被测点一定在球心轨迹面经过球心点的法线上。

图1 球心与接触面轨迹示意图Fig．1 Trajectory of center of the sphere and the contact surface

坐标测量机在对曲线、曲面进行测量时，所给出的是测头球心的轨迹，并不是实际接触点的坐标。所以，此时得到测量结果与实际存在偏差。在对类似航空发动机叶片的精确测量中，该误差是无法忽略的。通过对测头半径的补偿，得到更精准的点云数据，为之后的曲面拟合等高精度数据处理打下基础。

2 测头半径误差补偿

2．1 测头半径补偿原理

为实现测头半径补偿，必须知道被测曲面与测头接触点处的法矢。所以，测头半径补偿的核心问题就是确定被测曲面接触点处的法矢。

补偿原理是根据数学方法，求取测头中心点坐标沿测量方向的法矢量。在得到的法矢量的基础上，通过增加或减少测头半径的长度，得到实际测量点处的坐标。具体用公式可以表述为:以接触点处的法矢n近似代替被测叶片曲面实际接触点处被测曲面的法矢。实际接触点qi，j的计算公式为:

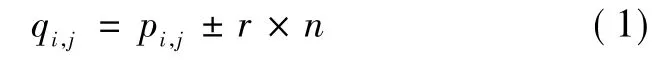
式中:r为测头半径，被测曲面为凸曲面时，取“+”号;被测曲面为凹曲面时，取“－”号。在此方法中，选取符号为“－”。

2．2 曲线补偿

实际的叶片型面测量中，往往采用扫描方式。具体过程为:将测头移动至初始测量点，保持某一坐标值不变(比如z轴)，移动测头使其在相应平面(XOY)内扫描直至边界点。然后，通过改变z轴坐标，按同样扫描方法扫描不同高度的曲线，直至遍布整个待测曲面。

曲线补偿具体过程如下。

在叶片测量中，坐标机得到曲线上的n个测量点。将曲线上得到的3个连续测量点设为P1、P2、P3，从而得到 3 个点坐标，分别为 P1(x1，y1)、P2(x2，y2)、P3(x3，y3)。测头半径补偿原理如图2所示。

图2 测头半径补偿原理图Fig．2 Pinciple of probe radius compensation

由于坐标机在对叶片测量的过程中得到的点云数据量很大，所以3个连续点的曲线段很小，可以理解为一段小圆弧上的临近点。P1、P2、P3满足圆方程:

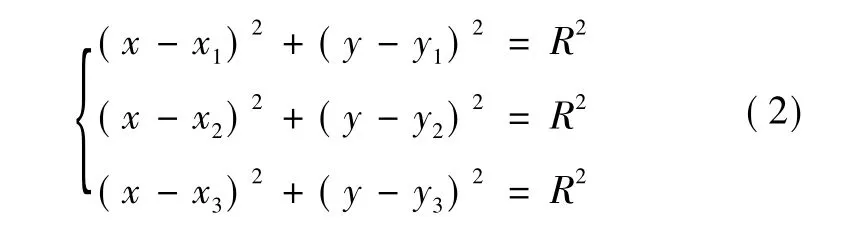
式中:(x，y)为接触点坐标。

对该方程进行求解，得到P1、P2、P3所在小圆弧的圆心坐标O(m，n)和圆的半径r。连接P2点和O点，线段P2O为P1、P2、P3所在小圆弧的法向线段。以P2为圆心，作一个半径等于测头半径R的圆，与线段P2O相交于点。

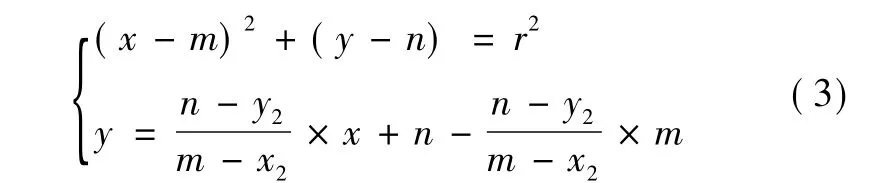
2．3 曲面补偿

根据空间内不共面的4个点，能确定一个球，且该球面唯一。在坐标机测量点P的周围一个非常小的区域内，可以近似地认为这一小块曲面是一个球面。在这个确定的球面上，所有点的法矢量都可以认为是球面上点与球心连线的方向。所以，这里根据被测量曲面上不共面的4个点来求解此微小区域的法矢。由于在叶片测量中，点云数据量密集，所以可以认为所选4个相邻点无限趋近。此时，所确定的球面法矢也可以认为是测量点处法矢。以下从数学的角度来阐述该方法的实现过程。

测量得到不同z值下的点云数据。根据测量的方向，把数据视为一个i行j列的数组。若要对其中某点Pi，j进行补偿，则可以取 Pi，j－1、Pi，j、Pi，j+1、Pi+1，j4 个点。曲面补偿原理如图3所示。

图3 曲面补偿原理图Fig．3 Principle of curved surface compensation

当选取4点构成的曲面趋近于无限小时，将其近似认为一个球面。将4个点构成球面的球心坐标设为Oi，j，确定的法矢为 Pi，j、Oi，j这 2 点的连线。根据法矢方向，将测量点在空间内移动一个测头半径的长度，以解算实际点坐标。法矢量为:

通过对上述数值进行单位化处理，即可得到被测点的单位法向矢量。补偿后，所求得的实际接触点Pi，j的坐标为:

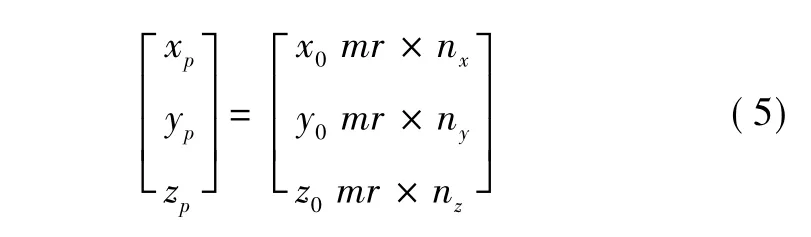
式中:O(x0，y0，z0)为球心点坐标。

根据补偿后的点拟合而成的曲面，即为被测叶片的实际曲面。

3 测头半径补偿仿真试验

判断测头半径补偿方法是否较其他方法存在优势，主要从补偿精度和补偿所耗时间两个方面入手。补偿精度主要指补偿后数据的真实度。补偿所耗时间则是在需要补偿大量点云数据的情况下，补偿程序的运行时间。理想的情况是在耗费很少运行时间的同时保证补偿的高精度。但是，在实际测量中，高精度往往意味着耗费较长的时间。

为了对该方法进行精度分析，在Matlab中编写程序，以实现本文所提出的补偿方法。利用本文提出的补偿方法，进行测头半径补偿的仿真试验。

仿真试验具体过程为:从坐标机测量得到点云数据中截取121个连续点。测量使用的坐标机测头半径为0．2 mm。运行程序得到实际接触叶片曲面的点坐标。求出每一个补偿得到的实际接触点与理论值的差值。将坐标机测量点进行仿真，得到的实际接触点坐标与接触点坐标理论值 Q(rn，sn，tn)，并进行比对，n=1，2，…，120。分别求，并求出最大值。此时，根据测量原理，z'值不变。补偿结果为:x=rn－=0．000 677 696，y=(sn－)max=8．248 79e-05。

通过比较2种方法的补偿结果，可以看出，本文所提出的快速补偿方法与其他算法的误差非常小，几乎可以忽略不计，从而验证了本方法能够保证精度。

补偿所耗时间可以用方法的计算量来表征，计算量越大，补偿耗时越多;反之亦然［6-9］。在本文所述方法中，补偿数据的计算主要有求解圆或球的特征点、与直线的交点组成，根据点云数据的具体数目来决定循环的次数，得到总的计算量。本文方法即使在大量点云数据的情况下，计算量也是非常少的。

如果在实际测量中需要更高的精度，可以提高点云数据的采集密度，通过更密集的数据来获取更高的精度;同时，也可以通过插补点的方法来得到更高的精度，但插补过程会占用一定时间。

综上所述，本文所提出方法能够在补偿耗时较少，即补偿效率尽可能高的情况下，保持很好的补偿精度。在实际叶片测量的测头半径补偿中，本文所提出的方法由于计算时间较少，对于提高叶片测量的效率具有重要意义。而与常用的存在原理误差的在线补偿法相比，本文方法的精度有显著提高，所以广泛适用于航空发动机叶片测量的坐标机测头半径补偿。

4 结束语

本文所提出的半径补偿方法，能够有效解决现有方法无法同时保证精度与补偿时间的问题。通过仿真试验结果可知，本文方法在计算速度快的同时，能够保证精度。该方法在叶片测量中具有很强的实用性，并对下一步叶片曲线、曲面拟合的精确度的提升具有重要意义，可以广泛应用于发动机叶片或其他复杂零件的测量。