基于矢量调制的多因子误差补偿方法研究

储开斌，江 楠，冯俊鹏

(常州大学信息与科学工程学院，江苏 常州 213164)

0 引言

自动平衡电桥法是电子元件参数测量的常用方法之一，具有测量精度高、测量范围宽、智能化程度高等优点。国际上许多著名的仪器制造企业，如Agilent、Fluke、Wayne kerr、HIOKI等，都将自动平衡电桥作为主要测量方法［1-2］。自动平衡电桥的核心电路是基于矢量合成的误差信号源。由于电路元件的非线性及分布参数的影响，其在宽频带范围内测量元件参数时，矢量合成的正交信号源不能保证严格的正交，使电桥在高频段测量时很难平衡，极大地限制了自动平衡电桥的应用［3-5］。为了实现宽带范围内对元件参数的测量，本文提出了一种矢量调制多因子误差补偿方法，解决了因正交误差对矢量信号合成的影响，提升了测量精度，拓展了自动平衡电桥的工作频带宽度。

1 自动平衡电桥测量原理

自动平衡电桥主要由激励信号源、I/V转换电路、混频、矢量检波、积分、矢量调制等模块组成［6-8］，其结构如图1所示。

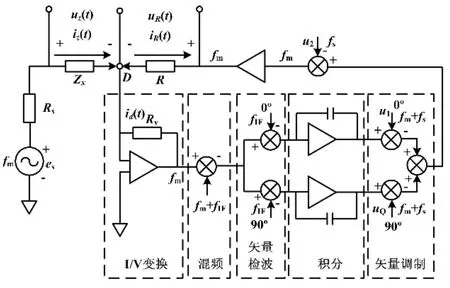
图1 自动平衡电桥结构图Fig．1 Structure diagram of automatic balance bridge

由图1可知:激励信号源es将频率为fm的测试信号加载到被测元件Zx两端;D点为虚地;uz为被测件两端电压;iz为流过被测件的电流。则电压电流用相量为:

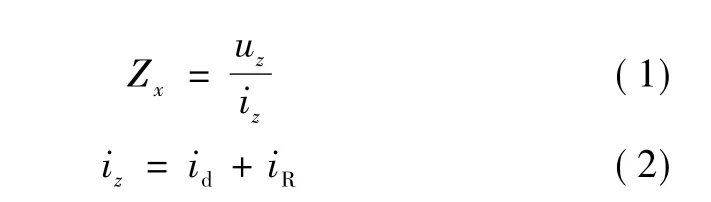
式中:id为误差电流;iR为流过标准电阻的电流。

I/V转换电路将误差电流id转换成电压信号，并送到混频器与频率为fIF+fm的本振信号u1进行混频，得到频率为fIF的中频信号。中频信号发送到矢量检波器，解调出id中的水平分量与垂直分量，经积分器积分后，在矢量调制器中与频率为fm+fs的信号uI、uQ进行矢量调制，最后再与频率为fs的本振信号u2混频，得到与测量信号频率相同的误差电压uR。通过积分电路的反馈调节，当id为零时，电桥达到平衡。此时，有:

由式(3)可知，该电桥通过将电流信号转换成电压信号，能测量被测件阻抗以及其他参数。该电桥测试信号频率fm的最大频带宽度为20 Hz～2 MHz［9-10］。当电桥的工作频率大于2 MHz时，由于矢量调制器在更高频率工作下，无法保证正交信号uI和uQ在频带范围内均达到准确的正交，使得该电桥在2 MHz以上无法达到平衡，从而限制了该电桥的应用范围。本文通过数字式多补偿因子，对矢量调制器的正交信号进行补偿，将该电桥的带宽提升到20 Hz～20 MHz，进一步拓展了该电桥的应用空间。

2 正交信号相位误差补偿方法

2．1 正交误差对电桥平衡的影响

矢量调制原理如图2所示。

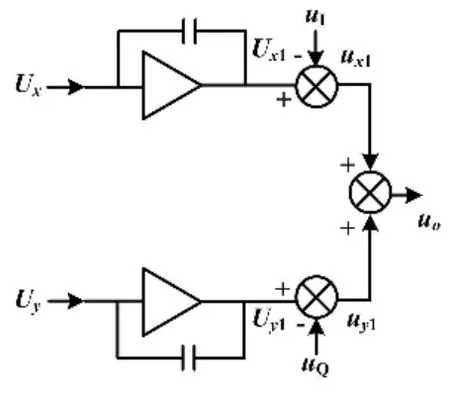
图2 矢量调制原理图Fig．2 Principle diagram of vector modulation

设矢量调制器所需输出信号为:

式中:uo为输出信号;UOI为输出信号x轴分量的幅值;UOQ为输出信号y轴分量的幅值;ω为信号的频率。

设:

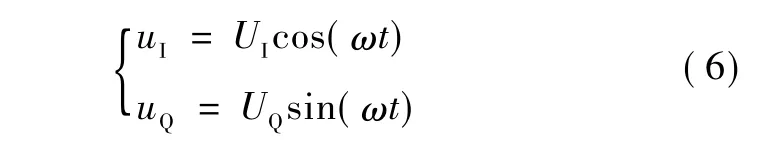
式中:uI、uQ为两路相位垂直的调制信号;UI为0°调制信号的幅值;UQ为90°调制信号的幅值。

式中:ux1、uy1分别为输出信号的x轴分量与y轴分量;Ux1、Uy1分别为积分电路输出的直流量;Ux2、Uy2分别为积分电路输出直流量经调制后的幅值。由积分电路调节Ux1与Uy1的值，可实现:

当电路满足式(2)时，电桥达到平衡。由于信号频率在20 Hz～2 MHz时，信号频率较低，电路能满足uI与uQ正交。随着信号频率的进一步升高，受电路分

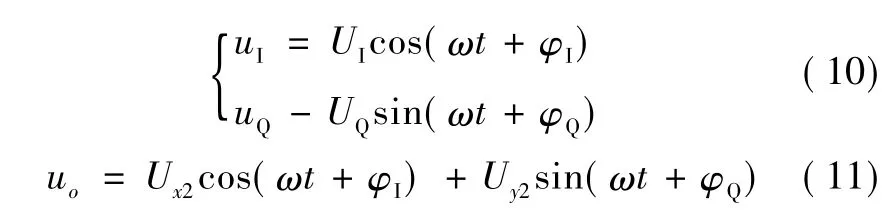
式中:φI、φQ分别为水平分量和垂直分量的相位误差。

2．2 多补偿因子的误差补偿原理

多补偿因子的误差补偿电路如图3所示。为了消除电路分布参数带来的相位误差影响，基于矢量合成原理，由Ux1和Uy1合成正交的两个向量。布参数的影响，uI与uQ将不能保证正交，实际输出与理论值在水平和垂直分量分别存在φI和φQ的相位误差，如式(4)所示。实际输出的矢量信号如式(5)所示。为达到电桥平衡的目的，积分电路需要输出较大的值才能达到平衡的要求，从而超出积分电路的输出范围，使电桥无法平衡。例如:当uI与uQ的夹角达到120°时，则ux1或uy1的幅度需要增加57．7%才能达到平衡。当测试信号的幅度为5 V时，矢量调制需要输出的电压为8．42 V，增加57．7%时达到 13．27 V。由于积分电路使用的放大器最大输出为10 V，实际输出电压超出了其输出范围，此时电桥无法平衡。

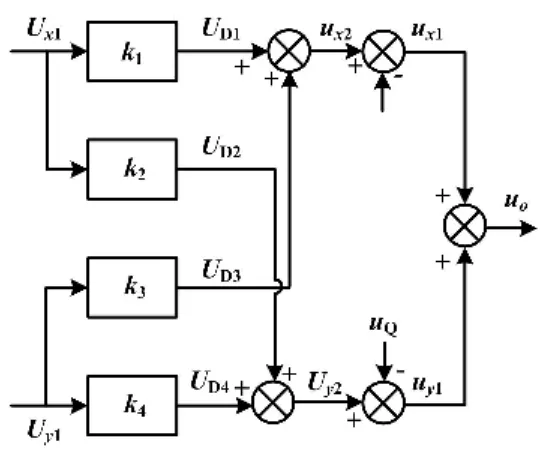
图3 误差补偿电路Fig．3 Circuit of error compensation

图3所示电路中，积分模块输出的直流量分别为Ux1和Uy1，经过因子K1～K4补偿获得UD1～UD4。其中:K1、K2、K3、K4由数字模拟(digital-to-amalag，D/A)转换器获得［11］，即:

然后，将 UD1和 UD3叠加得到 Ux2，UD2和 UD4叠加得到 Uy2，即:

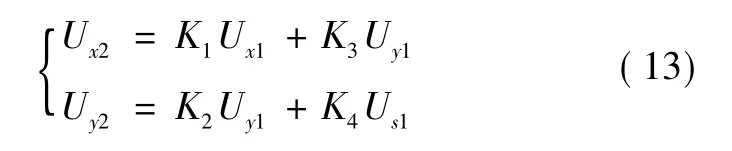
经过补偿后的补偿信号Ux2、Uy2分别对uI、uQ进行调制，得到满足系统要求的正交信号ux1、uy1。

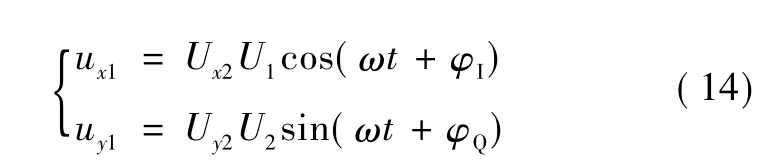
将ux1和uy1进行叠加，得到所需的误差电压信号，即:

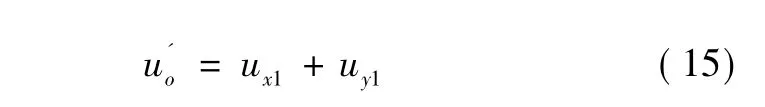
通过校准ux1与uy1之间的相位角，使实际合成的矢量信号与所需的矢量信号uo相同。比较uo与，可得:

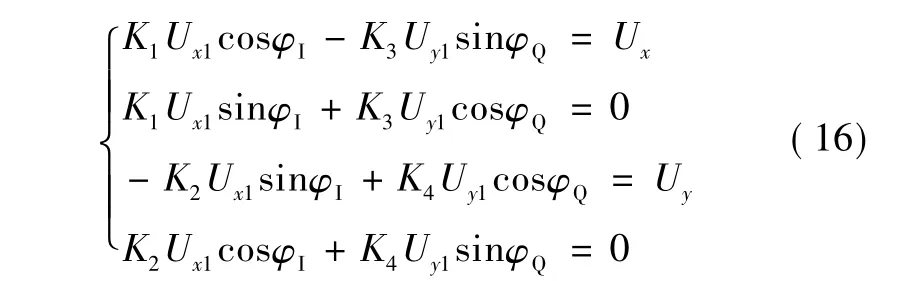
由此可得，补偿因子KI～K4为:

分布参数带来的相位误差 φI和 φQ有4种情形［12］，如图4 所示。

图4 多因子补偿示意图Fig．4 diagram of multi-factor compensation

图 4(a)中，ux1相位较 ux滞后 φI，uy1相位较 uy超前φQ。将ux1乘以 K1后，与 uy1乘以 K3的结果相叠加，得到ux;将ux1乘以K2后，与uy1乘以K4的结果，相叠加，得到uy。由此可得2个完全正交的信号。图4(b)、图4(c)、图(d)则是ux1、uy1相位滞后或超前不同组合的情形，都可以通过与补偿因子相乘后叠加，从而得到正交的信号。

2．3 补偿方法实现及实现结果

为了验证该方法的正确性，通过Multisim软件对该方法进行仿真验证，并通过相轨图观察在不同正交信号误差情况下的补偿效果。

设定水平分量信号的参数为fI=10 MHz、vI=5 V、φI1= － 10°、φI2=10°;垂直分量信号参数为 fQ=10 MHz、vQ=5 V、φQ1= －20°、φQ2=20°。将水平分量信号vI与垂直分量信号vQ分别接入示波器的A、B通道，以B/A方式输出得到相轨曲线，误差补偿前后的相轨图如图5所示。

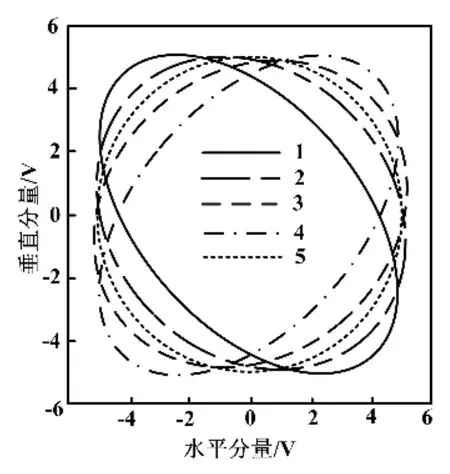
图5 误差补偿前后相轨图Fig．5 Phase orbit diagram with error compensation

曲线 1 为 φI滞后 10°、φQ超前 20°情况下的相轨曲线，呈现出偏向2、4象限的较扁椭圆。曲线2为φI滞后 10°、φQ滞后 20°情况下的相轨曲线，呈现出偏向2、4象限的较圆椭圆。曲线3为 φI超前10°、φQ超前20°情况下的相轨曲线，呈现出偏向1、3象限的较圆椭圆。曲线4为 φI超前10°、φQ滞后 20°情况下的相轨曲线，呈现出偏向1、3象限的较扁椭圆。将有误差的正交信号vI、vQ经误差补偿后输入示波器，得到补偿后的相轨曲线如曲线5所示。由曲线5可知，相轨图呈现出近似正圆的形状，表示此时水平分量信号vI与垂直分量信号vQ达到正交状态。图5表明，多因子补偿方法对具有相位误差的正交信号有较好的补偿作用。

3 试验测量与分析

为了验证多因子补偿方法的有效性，对补偿前与补偿后的样机进行了试验验证。在20 Hz～20 MHz频率范围内，将Agilent的标准件电阻及标准电容作为被测件进行阻抗测量，被测件参数如表1所示。

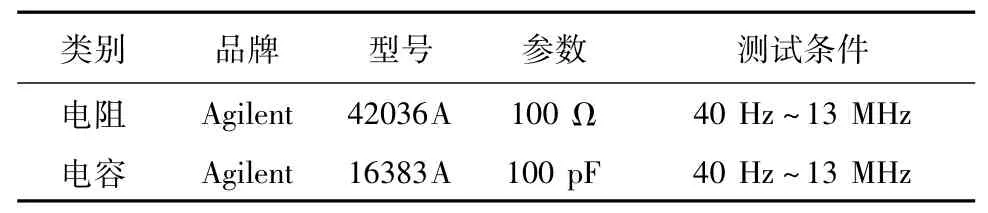
表1 被测元件参数Tab．1 Device parameter under test

在测试电压为1 V时，可得Agilent 100 Ω电阻测量结果如表2所示。

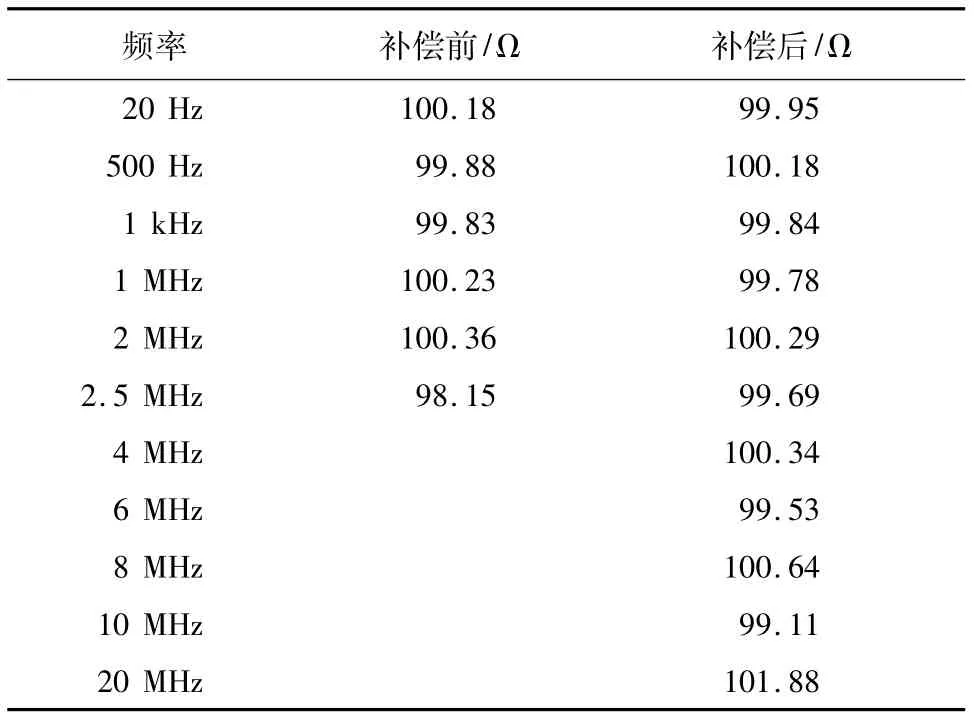
表2 电阻测量结果Tab．2 Resistance measurement results

测得Agilent 100 pF电容数据如表3所示。

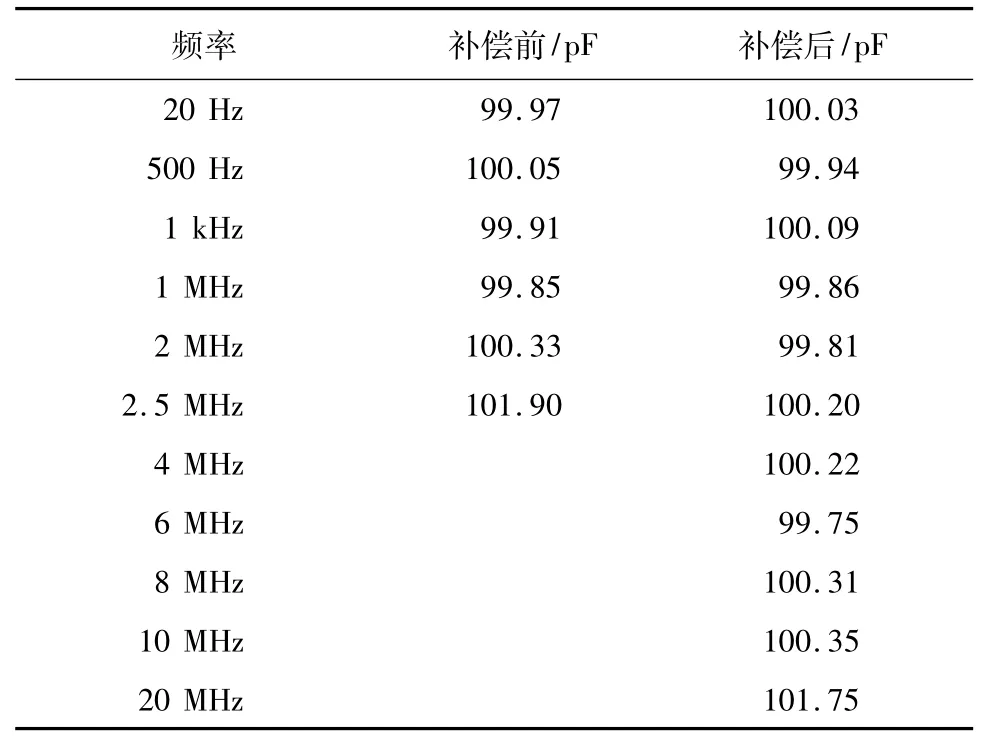
表3 电容测量结果Tab．3 Capacitance measurement results

由表2、表3可以看出，补偿前的样机测量范围在20 Hz～2 MHz有意义，超出2 MHz后电桥无法平衡，测得数据无意义。

在Agilent标准电阻及标准电容给定的40 Hz～13 MHz范围内，通过Agilent 4294A精密阻抗分析仪与系统原型机进行对比测试。在测试电压为0．5 V的条件下，测得电阻、电容的测量值与频率关系如图6所示。

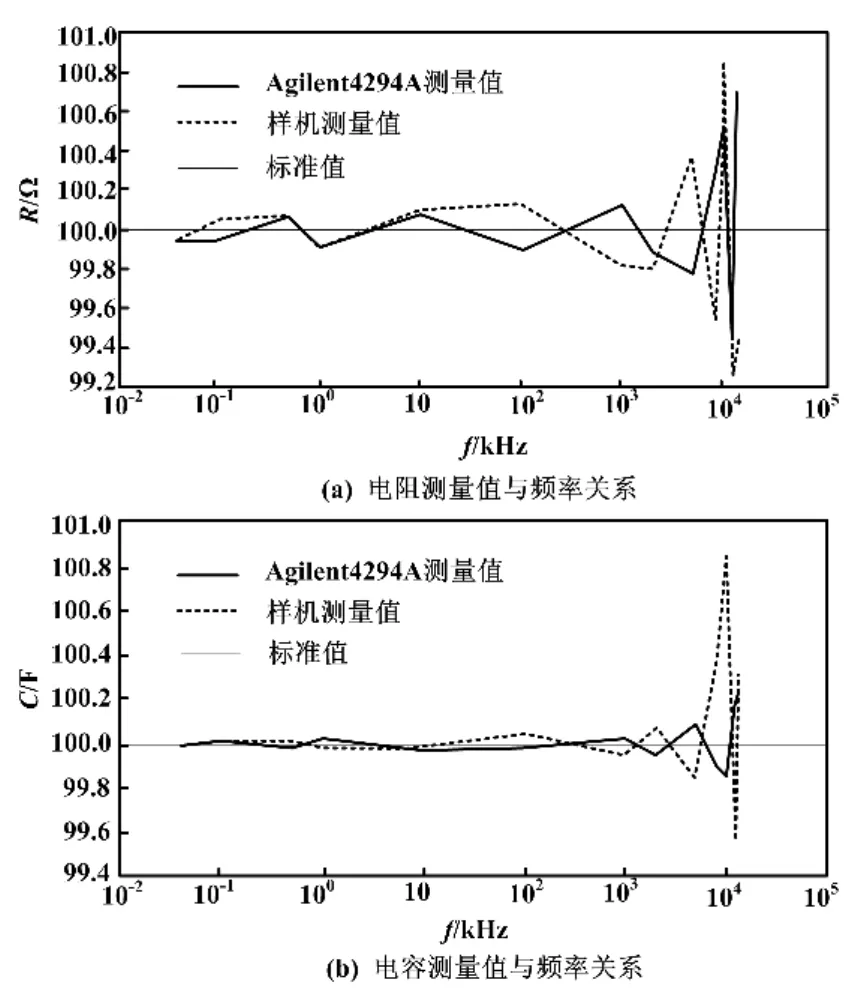
图6 测量值与频率关系图Fig．6 Relationship diagram between measurement and frequency

由图6可以看出，采用本文方法，在40 Hz～13 MHz范围内均能实现对被测件的精确测量。其中:在40 Hz～2 MHz范围内，测量精度为 0．2%;在2～13 MHz范围内，测量精度为0．87%。

由试验可知，通过在自动平衡电桥中引入数字式多因子补偿技术，将电桥的工作频率上限拓展到20 MHz，在测试频率范围内的测量精度接近 Agilent 4294A精密阻抗测量仪。该结果证明了本文所提补偿方法的有效性。

4 结束语

在采用自动平衡电桥法测量阻抗时，测试信号高频段由于电路分布参数影响，会造成矢量调制信号的正交误差，导致电桥无法平衡。为消除此误差，本文提出了一种数字式多因子补偿方法。通过多个补偿因子调节两路正交信号的幅度，经矢量合成得到标准的正交信号，解决了高频段自动平衡电桥无法平衡的问题，拓宽了电桥的应用范围。目前，该方法已成功应用于某公司的阻抗分析仪。