改进的分段盲源分离方法及其应用

李世龙，陈建宏

(太原卫星发射中心，山西 太原 030027)

0 引言

随着现代计算机技术及传感器技术的不断发展，基于振动信号分析的结构状态监测及故障诊断的应用越来越广泛。但受到被试对象结构复杂性、信号传递路径及噪声等因素的影响，传感器接收到的信号为各独立振源的非线性混合。而能否从实测信号中分离出纯净的源信息，很大程度上决定了故障诊断的准确性和可靠性［1-2］。因此，如何从实测非线性混合信号中分离出有效的振源信息具有重要的研究意义。

盲源分离又称盲信号分离，指通过观测到的混合信号来恢复原始信号或信源。近年来，盲源分离已成为信号处理领域的研究热点之一。盲源分离中较常用的假定是源信号的统计独立性。当各分量相互独立时，其被称为独立分量分析(independent component analysis，ICA)［3］。ICA 算法通常采用梯度法对目标函数进行寻优。但梯度法收敛速度慢、全局搜索能力差，其收敛性能受步长和初始值影响较大［4］。针对这些问题，近年来一些学者采用智能计算方法进行盲源分离的优化，如粒子群优化(particle swarm optimization，PSO) 算 法［5］、细 菌 觅 食 优 化 (baderialforaging optimization，BFO) 算法［6］和人工蜂群 (artificial bee colony，ABC)算法［7］等。然而，这些比较成熟的智能优化算法迭代参数较多，虽然全局搜索能力较强，但易陷入局部极值点，从而降低算法的分离精度。

为加快算法的收敛速度并保持好的分离精度，本文提出了一个更为高效的分段分离方法。将整个信号分离过程分为快速分离和精细分离两个阶段，兼顾算法的收敛速度和稳态性能。数值仿真及试验分析表明，所提方法真实有效。

1 盲源分离基本理论

盲源分离的数学模型可表示为:

式中:S(t)=［s1(t)，s2(t)，…，sn(t)］T为 n个位置的源信号;X(t)=［x1(t)，x2(t)，…，xm(t)］T为观测信号;A为m×n阶混合矩阵;N(t)为噪声信号。

盲源分离就是在源信号S和混合矩阵A均未知的情况下，求解混合矩阵A及其逆矩阵WT=A－1，使得输出信号逼近源信号。矩阵W称为分离矩阵。分离模型可表示为:

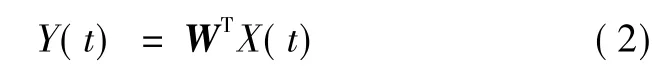
由式(2)可以看出，要实现输出信号Y逼近源信号S，则应使WT=A－1。因此，源信号的分离可归结为对分离矩阵W的求解［8］。

2 改进的分段盲源分离算法

为实现对非线性复杂混合信号的有效分离，本文将整个信号分离过程分为快速分离和精细分离两个阶段，以兼顾算法的收敛速度和稳态性能。快速分离阶段通过较少的迭代次数来较好地实现信号的初步分离，因此算法应具备较快的收敛速度。精细分离阶段通过选择适当的学习速率，可进一步提高信号的分离精度。

2．1 分段方法

对于不同时刻的两个信号yi(t)和yi(t)，两者的相关程度一般可由其二阶相关度rij(t)和高阶相关度hrij(t)进行衡量，即:

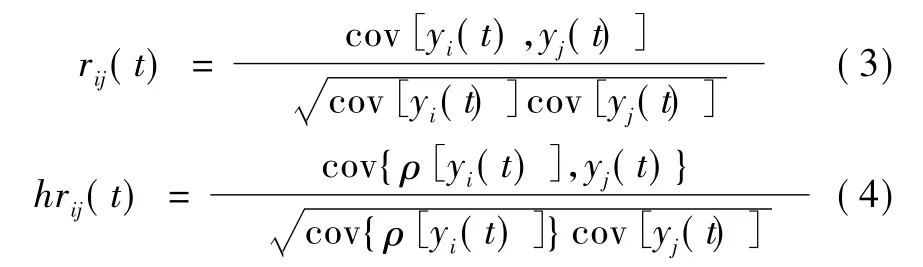
式中:i，j=1，2，…，m，且 i≠j;ρ［yi(t)］为非线性函数。

对于广义平稳信号 x(t)，在任意时刻 t，其均值为:

式中:λ∈(0，1)为遗忘因子。

Pij(t) =cov{ρ［yi(t)］，yj(t)}，Rij(t) =cov［yi(t)，yj(t)］，Qi(t)=cov{ρ［yi(t)］}。存在如下递归公式:

递归计算得到 Rij(t)、Pij(t)和 Qi(t)后，通过式(3)和式(4)，即可得到rij(t)和hrij(t)。

为评价信号的分离状态，定义第i路信号和第j路信号的关联程度为:

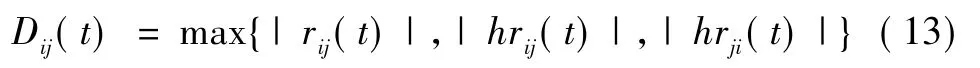
定义第i路信号的分离程度为:

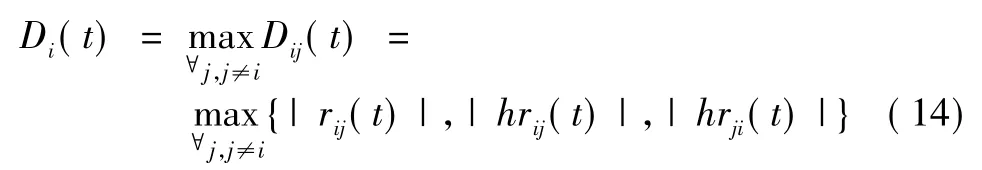
定义全部信号的整体分离程度为:

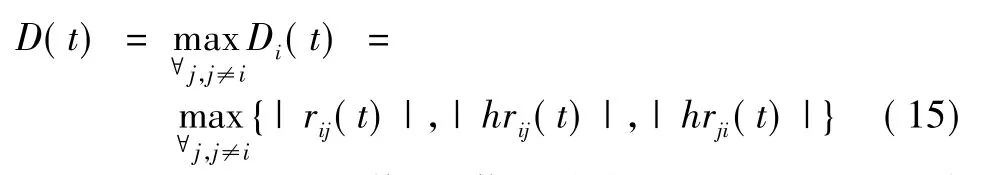
通过D(t)的取值，对信号分离进行阶段划分。当D(t)＞0．25时，为快速分离阶段;当 D(t)≤0．25时，则为精细分离阶段。

2．2 快速分离

快速分离的目标是通过尽可能少的计算达到较好的分离结果。考虑到粒子群算法具有较快的收敛速度，因此在快速分离阶段采用PSO算法进行寻优分离。

为简化算法，采用中心化方法，使独立分量及混合变量均值为零:

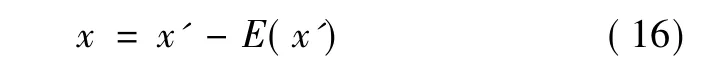
式中:x'为初始信号。

采用预白化方法对信号去相关，使其方差值为1。具体分解过程如下:

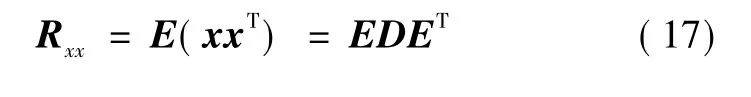
式中:Rxx为相关矩阵;E=(e1，e2，…，em)为正交阵，由Rxx特征值对应的特征向量组成;D=diag(d1，d2，…，dm)为对角阵，由Rxx的特征值组成。若白化矩阵V=则白化后的信号z=Vx满足:

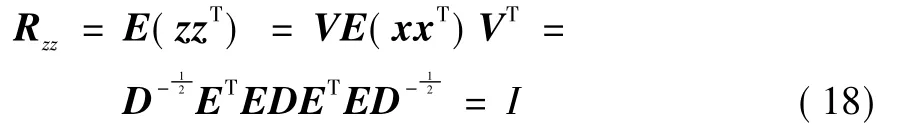
将负熵最大化作为分离的优化准则，其逼近公式如下:

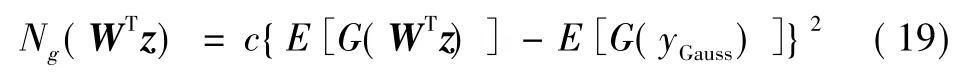
利用PSO算法中的动态因子和种群分类对式(19)进行寻优，即可实现负熵最大化。为避免重复分离同一信号，采用式(20)对分离矩阵W的各列进行正交化:

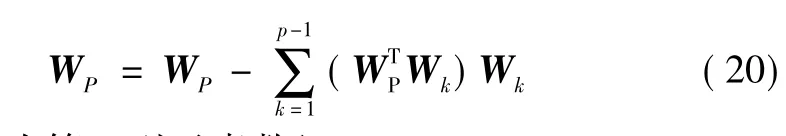
式中:WP为第 p列元素数组，p=1，2，…，m。

同时，为保证信号分离的稳定性，对W进行归一化处理:

综上可知，基于PSO的快速分离具体步骤如下。

①对观测信号X(t)进行中心化及预白化处理。

②设置初始分离矩阵W，对种群进行初始化，以WP作为粒子的位置向量。

③根据式(19)计算每个粒子的适应度值，存储每个粒子的个体极值及位置，并选出群体极值。

④更新每个粒子的速度和位置。

⑤采用式(20)和式(21)，对W进行正交化和归一化处理。

⑥判断算法是否达到最大迭代次数。若达到，则停止迭代，并输出最优位置向量WP;若未达到，则返回步骤③，继续迭代计算。

⑦计算分离信号Y=WTz。

2．3 精细分离

对于精细分离，应当选择较小的学习速率以保证算法的稳态性能。因此，选择较为平缓的函数来确定学习速率。本文采用如下迭代公式:

式中:Λ(t)=diag［η1(t)，η2(t)，…，ηm(t)］。

根据各路信号分离程度Di(t)，ηi(t)取值如下:

由式(23)可以看出，ηi(t)为信号分离程度Di(t)的非线性函数。因此，通过选择适当的取值，可充分提高信号的分离精度。

3 数值仿真及试验分析

3．1 数值仿真

为验证算法性能，选择具有不同峰度性质的两个亚高斯信号和一个超高斯信号作为源信号:

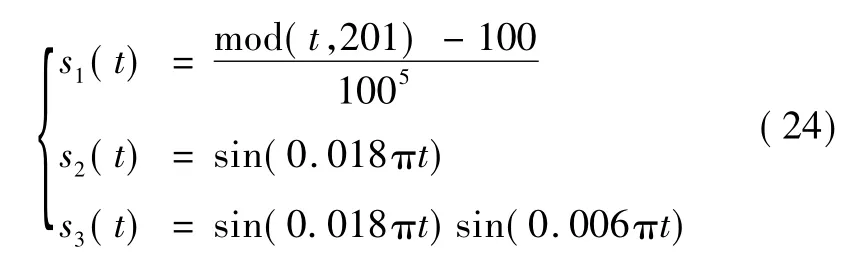
采样频率取3 kHz，采样长度为1 600。3个源信号的时域波形如图1所示。

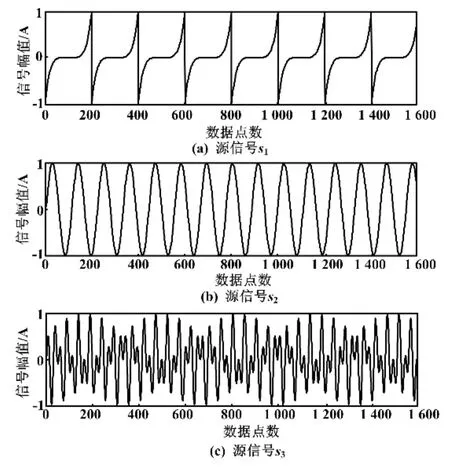
图1 源信号时域波形Fig．1 Time domain waveforms of source signals

随机产生2×3的混合矩阵A对3个源信号进行混合，得到的观测信号时域波形如图2所示。

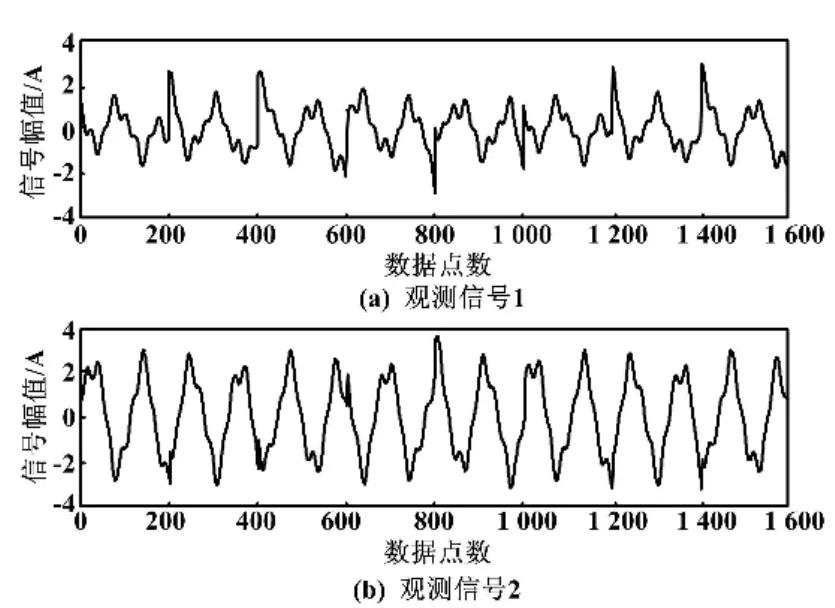
图2 观测信号时域波形Fig．2 Time domain waveforms of observed signals

分别采用文献［7］中基于ABC的盲源分离算法和本文提出的分段盲源分离方法，对混合信号进行分离，分离结果如图3和图4所示。

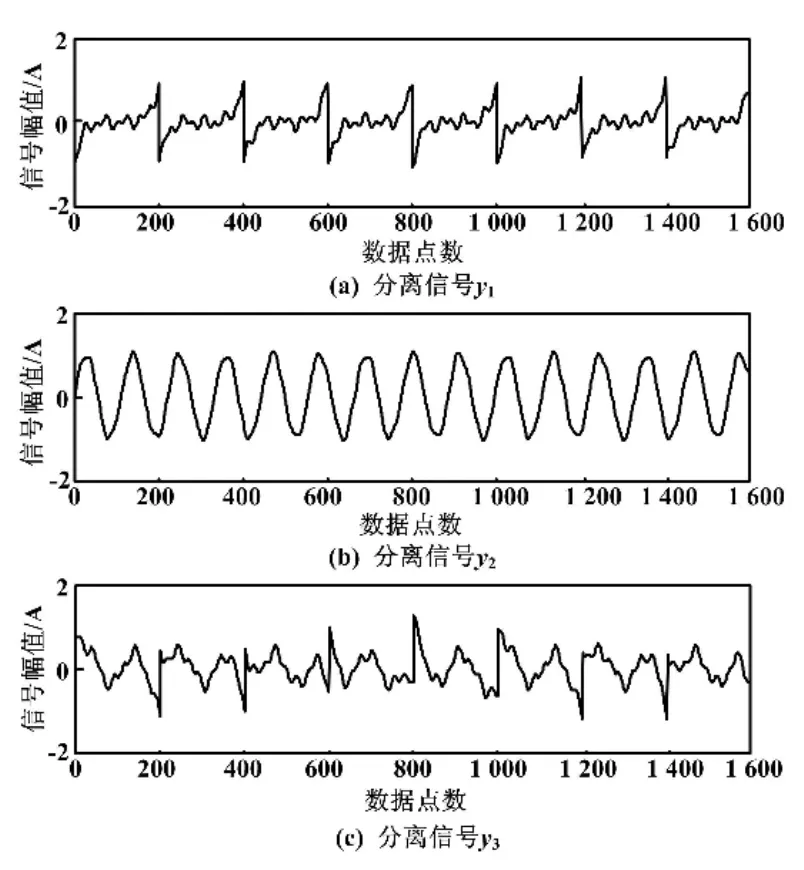
图3 ABC算法分离信号时域波形Fig．3 Time domain waveforms of separate signals of ABC algorithm

分离信号的质量，采用式(25)中的分离性能指标(performance index，PI)进行定量评估。

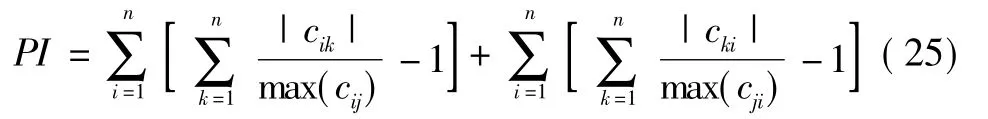
式中:C=(cij)=WA为全局矩阵，c为其元素;PI值越小，说明分离信号与源信号相似性越高，分离效果越好。

采用文献［7］中基于ABC的分离算法和本文算法，分别进行50次重复试验，记录下PI的最大值、最小值与均值，如表1所示。

表1 两种算法的PI对比Tab．1 Comparison of PI between two algorithms

图4 本文算法分离信号时域波形Fig．4 Time domain waveforms of separate signals of the proposed algorithm

图5 试验系统框架Fig．5 Framework of the experiment system

从PI最大值、最小值和均值的对比可以看出，本文算法分离信号的质量更好，比基于ABC的分离算法分离精度高约3个数量级，能够更准确地恢复出3个源信号。由此，验证了本文算法的分离精度和稳定性。此外，在多次重复分离试验中，本文算法平均用时仅为基于ABC分离算法的65．8%，说明该算法具有更快的分离速度。

3．2 试验分析

为验证本文方法在实测信号分离中的有效性，以一组预设故障的轴承振动信号为例，对其进行故障特征信号分离研究。试验系统框架如图5所示。

试验轴承预设的故障为典型的滚动体故障和内圈故障。经计算，轴承滚动体和内圈的特征频率分别为100．4 Hz和 123．5 Hz［9］。采样频率为 25．6 kHz，采样时间为1 s。其中，一个加速度传感器采集到的信号时域波形如图6所示。将该信号作为单一观测信号，采用本文方法对其进行单通道盲源分离。

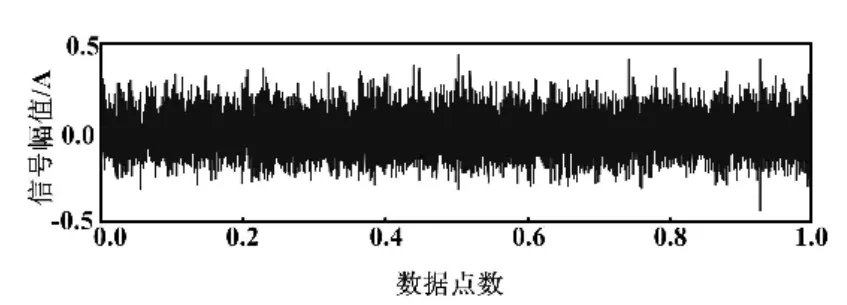
图6 故障轴承振动信号时域波形Fig．6 Time domain waveform of vibration signal of the fault bearing

为避免测试噪声及其他误差对分离结果的影响，在分离之前，先对原始信号进行多尺度形态差值滤波处理［10］。然后，采用本文方法对该信号进行分离。分离得到的两个信号分别如图7和图8所示。

图7 轴承滚动体故障特征信号示意图Fig．7 Fault characteristic signal of bearing rolling element

从图7可以看出，该频率为轴承滚动体的故障特征频率，且其二、三倍频效果非常明显，说明本文方法可以有效分离出轴承滚动体故障引起的冲击成分。

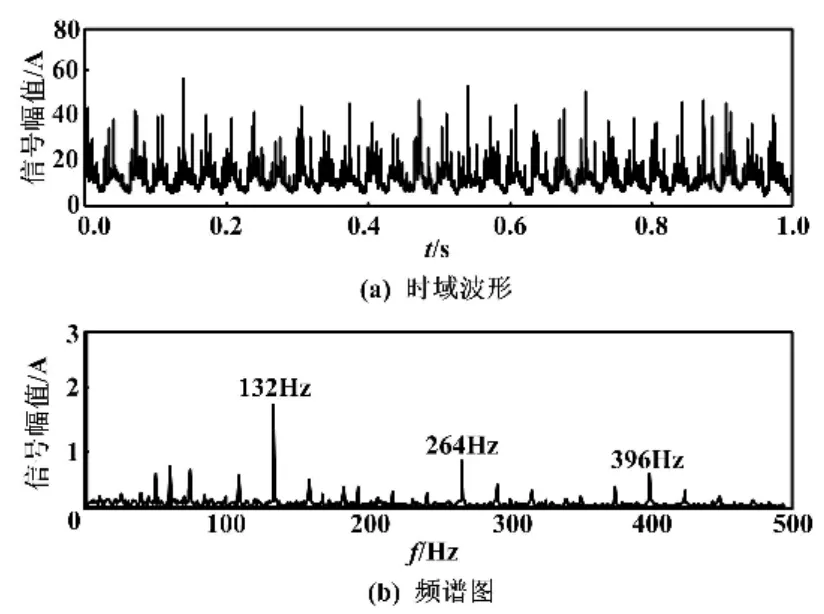
图8 轴承内圈故障特征信号示意图Fig．8 Fault characteristic signal of bearing inner ring

从图8可以看出，该频率为轴承内圈故障的特征频率，其效果非常明显;而其二、三倍频的提取效果则相对较弱。因此，采用本文方法可以实现对该预设故障轴承2种故障特征的有效提取。而基于ABC的分离算法未能有效分离出以上2种故障特征信号，故未列出其具体结果。

4 结束语

本文对振动信号分析中的盲源分离算法进行了研究，得出如下结论。

①将整个信号分离过程分为快速分离和精细分离2个阶段，并分别采用不同的分离方法，在保证收敛速度的同时，能够进一步提高信号的分离精度。

②多次重复数值仿真试验表明，本文算法较文献［7］中基于ABC的分离算法的分离精度高约3个数量级，具有更优越的分离速度、分离精度及稳定性。

③通过对某预设故障轴承的振动信号进行试验分析，其结果显示，本文方法能够有效分离出2种故障特征，而基于ABC的分离算法未能有效分离，证明了本文方法在轴承故障诊断中的有效性。