近三年高考中的“数学文化”试题赏析

江苏省睢宁高级中学北校 (邮编：221200)

《普通高中数学课程标准》(2017版)指出：数学文化是指数学的思想、精神、语言、方法、观点，以及它们的形成和发展；还包括数学在人类生活、科学技术、社会发展中的贡献和意义，以及与数学相关的人文活动.数学文化应融入数学教学活动.在教学活动中，教师应有意识地结合相应的教学内容，将数学文化渗透在日常教学中，引导学生了解数学的发展历程，认识数学在科学技术、社会发展中的作用，感悟数学的价值，提升学生的科学精神、应用意识和人文素养.将数学文化融入教学，还有利于激发学生的数学学习兴趣，有利于学生进一步理解数学，有利于开拓学生视野、提升数学学科核心素养.[1]

在高考中，或平时的教学实践、测试中，经常发现一些学生遇到涉及数学史、逻辑推理、数学思想、数学方法等“数学文化”色彩较浓的试题时，常被其表象所迷惑，认为很深奥、很神秘，没有耐下心来仔细阅读、审题，虽懂了相关知识，牢记住了相关的概念、公式、定理等，却不会解题.其实，只要揭开“数学文化”神秘的面纱，去掉无关紧要的前情叙述，抽象出相应的数学模型，题目还是极易解决的.现对近三年来高考数学中的部分“数学文化”试题分类赏析，以管窥一斑.

1 数学史类

数学史类试题，蕴涵着数学发展过程中若干重要事件、重要人物与重要成果，彰显出数学对人类文明发展的作用，能让学生体会到数学的科学价值、应用价值与文化价值[2]，让学生受到数学文化的熏染，激发学生学习数学的欲望.

图1

案例1(算法类) (2016年全国Ⅱ卷 文9理8)中国古代有计算多项式值的秦九韶算法，图1是实现该算法的程序框图.执行该程序框图，若输入的x=2，n=2,依次输入的a为2，2，5，则输出的s=( ).

A.7 B.12

C.17 D.34

赏析“秦九韶算法”是中国南宋时期的数学家秦九韶提出的一种多项式简化算法，是一种将一元n次多项式的求值问题转化为n个一

次式的算法，大大简化了计算过程.即使在现代，利用计算机解决多项式的求值问题时，“秦九韶算法”依然是最优的算法，极大地缩短了CPU运算时间.此法在西方被称作霍纳算法，是以英国数学家霍纳命名的.

对于此题，去掉前情叙述，可知就是考查算法问题，属于容易题. 答案C .

案例2(面积、体积类)(2017年浙江卷 第11题)我国古代数学家刘徽创立的“割圆术”可以估算圆周率π,理论上能把π的值计算到任意精度.祖冲之继承并发展了“割圆术”，将π的值精确到小数点后七位，其结果领先世界一千多年.“割圆术”的第一步是计算单位圆内接正六边形的面积S内，则S内=______ .

赏析“割圆术”、《九章算术》、《数书九章》等，都是中华民族的数学瑰宝，是灿烂悠久的中华数学文化的重要组成部分. 撩开题中“数学史”的面纱，可以发现此题就是求单位圆内接正六边形的面积，均属容易题. 将正六边形分割为6个等边三角形，则：

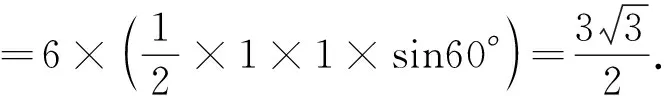
图2

案例3(概率类) (2018全国卷Ⅰ理10)图2是来自古希腊数学家希波克拉底所研究的几何图形．此图由三个半圆构成，三个半圆的直径分别为直角三角形ABC的斜边BC，直角边AB、AC．△ABC的三边所围成的区域记为Ⅰ，黑色部分记为Ⅱ，其余部分记为Ⅲ．在整个图形中随机取一点，此点取自Ⅰ、Ⅱ、Ⅲ的概率分别记为p1、p2、p3,则( )

A．p1=p2B．p1=p3

C．p2=p3D．p1=p2+p3

赏析古希腊数学中的毕达哥拉斯多边形数、勾股定理、勾股数、欧几里得与《几何原本》、尺规作图以及公理化思想等，对近代科学的发展都具有深远的影响，都是数学中的瑰宝. 去掉前情叙述，此题就是考查直角三角形面积公式、圆的面积公式、几何概型，属容易题，选A.另外，由于是选择题，可取特殊值a=5，b=3，c=4进行计算，快速得到答案.

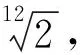
2 数学思想、数学方法、逻辑推理类

数学文化不仅指数学史以及数学概念、法则、公式、定理等这些表面的知识性的有形成分，还包括蕴涵于数学知识之中的数学思想、数学意识、数学精神和数学美等内在的观念性的无形成分[3].这些内在的观念性的无形成分是数学文化的核心，也就是把所学的数学知识都忘掉后剩下的可以终身受用的成分，用这些内在的观念性的无形成分可以进行思考、判断和逻辑推理，去提出、发现、分析和解决新问题.

赏析此题主要考查“数形结合”思想及“排除法”，属中档题.

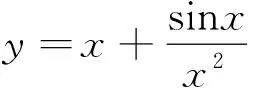
法二当x=1时，f(1)=1+1+sin1=2+sin1>2,故排除A、C,当x→+∞时，y→1+x,故排除B,满足条件的只有D，故选D.

赏析此题考查“分类讨论”思想或“数形结合”思想，以及逻辑推理.

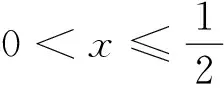
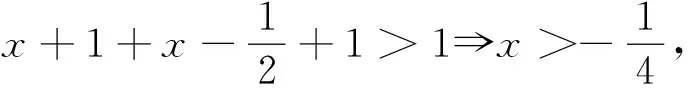
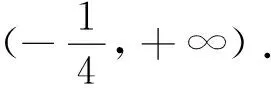
图3

案例8(1)(2016年全国Ⅱ卷 理14文16)有三张卡片，分别写有1和2，1和3，2和3.甲，乙，丙三人各取走一张卡片，甲看了乙的卡片后说：“我与乙的卡片上相同的数字不是2”，乙看了丙的卡片后说：“我与丙的卡片上相同的数字不是1”，丙说：“我的卡片上的数字之和不是5”，则甲的卡片上的数字是______.

(2)(2017年全国Ⅱ卷 理7文9)甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩，老师说：你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩.看后甲对大家说：我还是不知道我的成绩，根据以上信息，则( )

A.乙可以知道四人的成绩

B.丁可能知道四人的成绩

C.乙、丁可以知道对方的成绩

D.乙、丁可以知道自己的成绩

赏析这两题主要考查学生的逻辑思维能力(逻辑推理素养).

(1)因为丙的卡片数字之和不是 5，故丙的卡片数字应为1与2，或1与3，

当丙的卡片数字为 1与 2时，又因乙与丙的卡片上相同的数字不是1，则乙的卡片数字为 2 与 3，又因甲与乙的卡片上相同的数字不是2，故甲的卡片数字为 1 与 3．符合题意；

当丙的卡片数字为 1 与 3时，又因乙与丙的卡片上相同的数字不是1，则乙的卡片数字为 2 与3，此时甲的卡片数字只能为 1 与2，这与已知甲与乙的卡片上相同的数字不是2相矛盾．

综上知，甲的卡片数字为 1 与 3．

(2)由题意，看完后，甲对大家说：我还是不知道我的成绩，这就说明乙、丙的成绩应是一人为优，另一人为良. 由题意，这四人中有2位优秀，2位良好.

所以当给乙看过丙的成绩后，乙定能知道自己的成绩(若丙为优，则乙为良；若丙为良，则乙为优).

同样地，当给丁看过甲的成绩后，丁也定能知道自己的成绩(若甲为优，则丁为良；若甲为良，则丁为优).故选D.