基于ABAQUS有限元强度折减法的边坡稳定性分析

夏园园

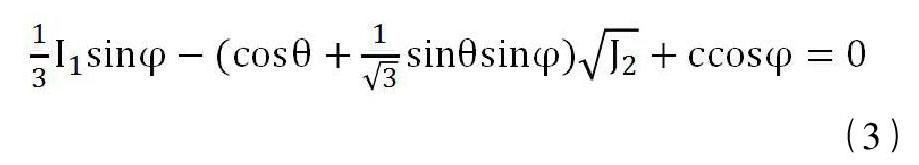
摘要： 将有限元强度折减法与ABAQUS软件相结合，充分运用ABAQUS软件强大的数据处理功能以及动态显示广义塑性应变和塑性区的开展情况，以此来判断边坡的整体稳定性。在ABAQUS软件实施有限元强度折减法的过程中，通过不断线性增大强度折减系数Fr的大小，得到多组不同的抗剪强度参数cm和φm值的组合以及塑性区的开展情况。当塑性区趋于贯通且广义塑性应变和位移均发生突变时，则此时边坡处于临界破坏状态，对应的强度折减系数Fr即为给定条件下的最小稳定安全系数。通过一个典型分层边坡的实例分析，表明该法可以准确求解安全系数和对应的滑动面位置，在复杂条件下的边坡稳定性分析中同样是简便实用的。

Abstract： Combining the finite element strength reduction method with the ABAQUS software， the ABAQUS software's powerful data processing function and the dynamic display of the generalized plastic strain and plastic zone are fully utilized to judge the overall stability of the slope. In the process of implementing the finite element strength reduction method by ABAQUS software， by continuously increasing the magnitude of the strength reduction factor Fr， the combination of different sets of shear strength parameters cm and φm and the development of the plastic zone are obtained. When the plastic zone tends to penetrate and the generalized plastic strain and displacement are abrupt， the slope is in a critical failure state， and the corresponding strength reduction factor Fr is the minimum stability safety factor under given conditions. An example analysis of a typical layered slope shows that the method can accurately solve the safety factor and the corresponding sliding surface position， which is also simple and practical in the slope stability analysis under complex conditions.

關键词：边坡稳定性分析；ABAQUS软件；有限元强度折减法；安全系数

Key words： slope stability analysis；ABAQUS software；finite element strength reduction method；safety factor

中图分类号：U416.1+4 文献标识码：A 文章编号：1006-4311（2018）31-0190-05

0 引言

边坡稳定性分析研究历来是岩土工程界亟待解决的重点和难点课题，如何准确分析和把握边坡的稳定性，对于提高工程建设质量和保证人民生命以及财产安全具有非常重要的理论和现实意义。经过众多科研人员的积极探索和创新，在边坡稳定性分析理论和计算方法等方面取得了重大突破，到目前为止已经提出十几种边坡稳定性分析方法。目前，在工程领域得到广泛应用的分析方法主要是极限平衡法和有限单元法[1]。极限平衡法由于计算公式和原理简单，易为广大工程技术人员所接受，但该方法没有考虑土体自身的应力应变关系和实际工作状态，从而也无法得到边坡内的应力与变形协调关系及其在加卸载过程中的发展过程。滑动面的确定需要较多的工程经验，还需要事先知道边坡的滑动面位置以及形状，从而极大的限制了其在边坡稳定性分析中的应用。随着计算机技术在各个领域的应用和发展，尤其在考虑岩土材料复杂本构关系的过程中，有限单元法在边坡稳定性分析中发挥出了更大的优势，更能反映边坡岩土体的实际工作状态。

有限单元法由于克服了极限平衡法的众多缺点，并且考虑了岩土体的弹塑性本构关系以及变形协调关系；能够模拟各种复杂边坡的变形失稳破坏过程，对边坡的应力分布特征、塑性区范围和位移等进行有效模拟，在处理各种复杂的边界条件以及材料的非均匀性和各向异性等方面相对于极限平衡法表现出了明显的优势。因此，随着数值分析方法的发展，一种基于强度折减技术的弹塑性有限元法[2～5]在边坡稳定性分析中得到了广泛应用。本文采用大型非线性分析软件ABAQUS软件，结合有限元强度折减法进行土质边坡稳定性分析，在给定的评价标准下，综合确定边坡最小稳定安全系数。并运用ABAQUS软件强大的数据处理功能，通过塑性应变云图随时间的发生和发展过程来反映边坡的渐进破坏过程，以此作为评价边坡稳定性的重要依据。

1 ABAQUS软件介绍

ABAQUS软件是一款功能强大的非线性有限元分析软件之一，可以模拟非常庞大复杂的结构系统，尤其是在处理非线性岩土材料方面表现出突出的优势。ABAQUS软件能够计算各种不同材料、模拟各种外荷载作用过程以及处理各种接触情况的非线性组合问题，且具有强大的后处理功能。使用方便，能够快速地为复杂问题建立模型，计算精度较高。因此，在工程界得到了广泛应用。ABAQUS软件包含种类丰富的单元库，可以模拟任意几何形状，且具有丰富的材料模型库可以模拟大多数典型材料的性能。尤其是针对土体这种特殊材料，在处理结构面接触非线性问题、几何及边界条件非线性问题以及地应力平衡等复杂外荷载作用方面都收到了良好的效果。实施有限元强度折减法之前，需要事先定义边坡达到临界破坏状态的评价标准，本文以坡体顶点位移拐点和塑性区贯通作为判据来综合评价边坡的整体稳定性。

2 有限元强度折减法的基本原理[6]

有限元强度折减法是由Zienkiewicz等在1975年首次提出的，后被众多学者广泛引用。他们首先提出一个抗剪强度折减系数的概念，其基本定义是[2]：在外荷载保持不变的情况下，边坡内土体所能提供的最大抗剪强度与外荷载所产生的实际剪应力之比。在极限状态下，外荷载所产生的实际剪应力与抵御外荷载所发挥的最低抗剪强度即按照实际强度指标折减后所确定的、实际中得以发挥的抗剪强度相等。当假设边坡内所有土体的抗剪强度的发挥程度均相同时，此时的抗剪强度折减系数相当于边坡整体稳定安全系数，又称为强度储备安全系数。而强度储备安全系数与极限平衡法中所给出的稳定安全系数在概念上是一致的。其基本原理是：将岩土体抗剪强度指标c、？渍值同时除以一個强度折减系数Fr，得到一组新的抗剪强度参数cm、？渍m值，计算过程中，通过不断线性增大折减系数Fr，得到多组不同的cm和？渍m值的组合。当边坡岩土体达到临界破坏状态时所对应的折减系数Fr即为给定条件下的边坡最小稳定安全系数[4]。其中，cm、？渍m分别根据公式（1）和（2）求得，弹性模量E和泊松比？滋均假设为定值，即不随折减系数的改变而变化。

3 ABAQUS有限元法数值模拟及边坡稳定的评价标准

ABAQUS软件是目前在处理岩土工程问题时通用的一种非线性有限元软件，其包含种类丰富的材料模型库，因此可以更准确的模拟土体这种特殊材料，在求解岩土力学中复杂非线性问题方面表现出了更加突出的优势。

3.1 屈服准则的选取

影响边坡发生失稳破坏的关键因素是岩土体的抗剪强度，当最大剪应力达到破坏极限时，土坡将发生失稳破坏。基于此，本文在用强度折减系数法求解边坡稳定问题时，采用的是理想弹塑性模型，屈服准则采用Mohr-Coulomb破坏准则：

3.2 流动法则的选取

总的来说，对于同一类型材料，采用非关联流动法则所得的破坏荷载比采用关联流动法则所得的破坏荷载要小，如果忽略剪胀角（？覫=0），将会得到比较保守的结果。岩土类材料不适应关联流动法则，由此算出的变形与实际变形有较大的误差，尤其是应用剪切型屈服面会算出过大的剪胀现象。但非关联流动法则只能在一定程度上减少剪胀现象，且值的选取具有很大的随意性，增大了计算土性参数与实际土性参数的差距，带来新的计算误差[3]。综合考虑各种因素后，本文中采用关联流动法则，即取=。

3.3 边坡失稳的评价标准

边坡失稳的评价标准直接影响到有限元强度折减法计算结果的正确性。目前判断土坡是否达到临界破坏状态的评价标准可以归纳为以下三种[7]：①以数值计算结果收敛与否作为评价标准，该评价标准与所采用的有限元计算方法有关。②以特征部位的水平位移关于强度折减系数关系曲线图上的位移拐点作为评价标准。③以塑性应变等值线云图中的滑动破裂面是否形成连续贯通区域作为评价标准。

4 工程实例分析

4.1 工程概况

某土质边坡[4]几何模型示意图如图1所示，该土质边坡坡高为h=10m，计算总宽度b=18m，坡角β=45°，土层为弹塑性材料，共分为三层，各土层名称及基本物理力学参数如表1所示，采用Mohr-Coulomb本构模型进行静力分析。边界条件为：左右两侧面约束水平方向位移，底部约束水平和竖直方向位移，外荷载仅考虑重力荷载的作用。现在采用大型非线性有限元分析软件ABAQUS软件结合有限元强度折减法对该土质边坡的渐进破坏过程进行详细模拟，以求解最小稳定安全系数和确定滑动面位置。

4.2 强度折减法在边坡工程中的实现过程

假设场变量初始值为0.50，线性增加场变量大小，使场变量在0.50-2.00之间变化。根据强度折减法的基本原理及其在ABAQUS中的实现流程，得到各土层随场变量变化的强度折减参数如表2所示。

4.3 网格划分

根据该边坡几何特点和计算精度要求，单元形状设置为四边形，采用扫掠划分技术，并以四节点平面应变单元作为单元类型，总共划分了574个网格单元，得到的有限元网格划分示意图如图2所示。

4.4 数值模拟结果分析

通过计算可知，本算例在第二个分析步的0.593643时无法收敛，计算终止。这是因为强度折减到某一程度之后，土坡就已经失稳。下面来具体分析如何确定安全系数和滑动面位置。

4.4.1 确定安全系数

利用ABAQUS软件数据处理功能Operate on XY data中的Combine函数来建立强度折减系数FV1随坡体顶点水平位移U1之间的变化关系曲线图如图3所示。由图3可知，若以数值计算不收敛作为土坡稳定的评价标准时，对应的安全系数Fs=1.390，若以位移拐点作为评价标准时，则安全系数为Fs=1.303，而根据极限平衡法（Morgenstern-Price法）得到的安全系数和最危险滑动面位置如图4所示，此时安全系数为Fs=1.296。

以塑性区贯通与否来确定安全系数大小：通过ABAQUS模拟边坡处于天然状态下的失稳破坏过程，得到的塑性区开展情况随折减系数变化过程如图5中的（a），（b），（c），（d）和（e）所示。

图（a）-（e）清晰的呈现了土坡发生失稳的全过程，即一开始是土坡坡脚处首先出现屈服，然后慢慢的向坡顶延伸，直到出现塑性区贯通现象。塑性区刚刚贯通时对应的安全系数为Fs=1.305，这和以数值计算不收敛作为土坡稳定的评价标准得到的安全系数相差较大，与以位移拐点作为评价标准得到的安全系数很接近，这是因为当塑性区贯通之后位移自然快速增加，而计算并不一定不收敛。

以数值计算不收敛得到的安全系数为Fs=1.390，若以坡体顶点位移拐点得到的安全系数为Fs=1.303，塑性区贯通时的安全系数Fs=1.305，而极限平衡法得到的安全系数Fs=1.296。可见，以坡体顶点位移拐点和以塑性区贯通得到的安全系数相当接近，两者几乎是同时发生的，且两个安全系数与极限平衡法得到的稳定系数相差不大，但与以数值计算不收敛得到的安全系数相差较大。因此，实际工程中为偏于安全考虑，我们可以以坡体顶点位移拐点和塑性区是否贯通两个评价标准来综合判断边坡的整体稳定状态。

4.4.2 确定滑动面位置

实际上根据上一步的塑性应变分布就可大致的确定出滑动面的位置，这里也可以通过计算终止时的总位移等值线云图来确定滑动面的位置。计算终止时的总位移等值线云图如图6所示，由图6可以很清楚的判断出滑动面的位置，其与图4极限平衡法得到的结果相一致，两者都呈现出圆弧形滑动面，并且通过坡脚点。然而，在某些特殊情况下，根据总位移等值线云图仍无法判断出滑动面的位置。此时可以根据计算终止时的最后一个增量步的增量位移来判断出滑动面的位置。本算例计算终止时的增量位移等值线云图如图7所示，与计算终止时的总位移等值线云图和极限平衡法得到的结果非常吻合。表明这两种方法是直观、有效的。

5 结语

本文将大型通用非线性有限元分析软件ABAQUS软件与有限元强度折减法相结合，提出以数值计算不收敛、特征部位的位移拐点和塑性区贯通作为判断边坡失稳的评价标准，可充分运用ABAQUS计算结果的动态云图显示技术，形象的描绘出边坡的渐进破坏过程，为准确判断安全系数和确定滑动面位置提供可靠依据。算例分析表明：以坡体顶点位移拐点和塑性区贯通为评价标准求得的安全系数与极限平衡法所得结果比较接近，因此本文所采用的方法是合理可行的。尤其是针对外界条件复杂的边坡工程，在土层多样、支护结构复杂，同时考虑地下水等特殊因素时，该法是简便可靠的方法。

参考文献：

[1]陈祖煜.土质边坡稳定分析-原理·方法·程序[M].北京：中国水利水电出版社，2003.

[2]栾茂田，武亚军，年廷凯.强度折减有限元法中边坡失稳的塑性区判据及其应用[J].防灾减灾工程学报，2003，23（3）：1-8.

[3]郑颖人，赵尚毅，张鲁渝.用有限元强度折减法进行边坡稳定分析[J].中国工程科学，2002，4（10）：57-61，78.

[4]张鲁渝，郑颖人，赵尚毅，等.有限元强度折减系数法计算土坡稳定安全系数的精度研究[J].水利学报，2003（1）：21-27.

[5]连镇营，韩国城，孔宪京.强度折减有限元法研究开挖边坡的稳定性[J].岩土工程学报，2001（4）：407-411.

[6]费康，张建伟.ABAQUS在岩土工程中的应用[M].北京：中国水利水电出版社，2009.

[7]李春忠，陈国兴，樊有维.基于ABAQUS的强度折减有限元法边坡稳定性分析[J].防災减灾工程学报，2006，26（2）：207-212.