基于滑动面倾角权重的边坡稳定性评价

卢玉林,薄景山,陈晓冉,王 丽

(1.防灾科技学院防灾工程系,北京101601；2.中国地震局工程力学研究所,黑龙江哈尔滨150080；3.中国兵器工业北方勘察设计研究院有限公司,河北石家庄050011)

基于滑动面倾角权重的边坡稳定性评价

卢玉林1,2,薄景山1,2,陈晓冉3,王 丽1

(1.防灾科技学院防灾工程系,北京101601；2.中国地震局工程力学研究所,黑龙江哈尔滨150080；3.中国兵器工业北方勘察设计研究院有限公司,河北石家庄050011)

基于点安全系数评价边坡稳定性的优势,通过弹性力学基础理论得到一点单元体的应力状态表述,以摩尔-库伦准则获得基于空间应力状态的安全系数表达形式。在确定边坡安全系数最小值的前提下,通过识别潜在滑动面,以滑动面倾角为权重,建立最小安全系数与整体安全系数的关系,最终以整体安全系数评价边坡的稳定性。

边坡稳定性；整体安全系数；点安全系数法；滑动面倾角

0 引 言

边坡稳定性是岩土工程研究的热点问题之一,稳定性评价自极限平衡理论以来已有近百年的历史。目前,多数的问题以极限平衡法为基础,而后发展了诸如有限元极限平衡法等[1]。传统瑞典圆弧法认为滑体是刚体,忽略了材料本身参数对稳定性的影响,并不能真实反映材料的应力分布和材料的抵抗能力。因此,以点安全系数法评价边坡稳定性显得格外重要[2- 6]。点安全系数法以应力分布为基础,结合不同的强度准则完成稳定性的评价[7-9]。其优点在于无需假设滑动面的形式和位置,通过计算安全系数的最小值来表达边坡的稳定状况。不同位置坡体的安全系数各异,与极限平衡理论中强调整体安全系数并不相同。文献[8]用点安全系数法分析了三维边坡的稳定性,并论证了该方法的应用条件,提出了整体安全系数的修正表达式,突出了应力空间效应。文献[3]通过寻找潜在的岩体抗剪强度来计算边坡的点安全系数,评价结果偏于保守,与传统的简化Bishop法结果具有一致性。文献[10]以最大剪应力对应的抗剪强度与最大剪应力之比作为新的安全系数,也是基于点的应力状态。

基于点安全系数评价边坡稳定性的优势,本文通过弹性力学基础理论得到一点单元体的应力状态表述,并以摩尔-库伦准则获得基于空间应力状态的安全系数表达形式。在确定边坡安全系数最小值的前提下,通过识别潜在滑动面,以滑动面倾角为权重,建立最小安全系数与整体安全系数的关系,最终以整体安全系数评价边坡稳定性。

1 边坡一点的应力状态

1.1 点安全系数的定义

边坡在外荷载作用下一点的应力状态为空间形式,单元体每个面上均有3个应力分量。根据六面体切应力互等定理可知,相邻面上的切应力大小相等。因此,独立的应力分量个数可简化为6个。用6个应力分量来表述安全系数是复杂的,以主应力为代表的单元体在表达形式上会更加简捷[11]。假设边坡任意一点单元体主应力为σ1、σ2和σ3(见图1a),任意斜截面上的应力可分解为法向应力σ和切向应力τ(见图1b)。

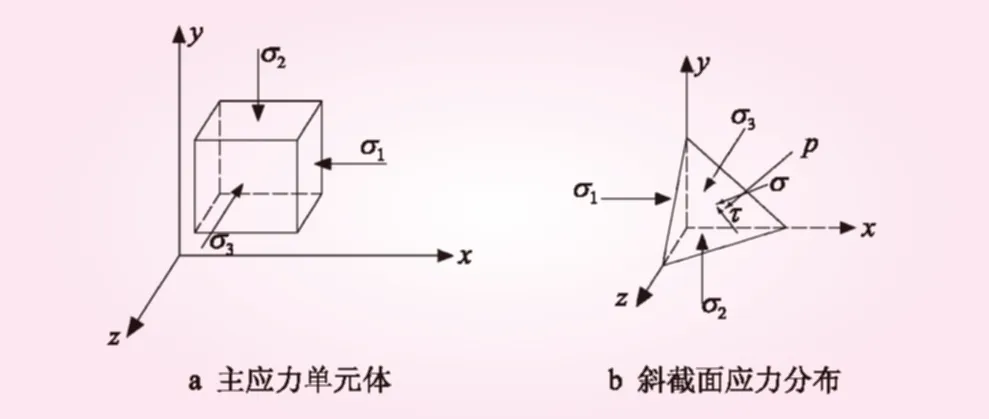
图1 主应力单元体及斜截面应力分布

由摩尔-库伦准则可知,单元体上一点的安全系数可通过斜截面上的抗剪强度与下滑力之比来表示。从弹性力学的定义可知,斜截面与坐标轴的夹角一般为锐角,方向余弦为正值,所以计算的最小安全系数Fmin可通过单元体上的大小主应力表示,即

(1)

式中,c为土体粘聚力；φ为内摩擦角。

由式(1)可知,最小安全系数Fmin取决于单元体中的最大和最小主应力,这与忽略中间应力的摩尔-库伦准则相符。单元体失稳时只与2个主应力有关,而第三个主应力方向与斜面平行,是一对自相平衡的力,对斜面上的应力不产生任何影响。单元体空间应力莫尔圆见图2。当岩土强度指标确定时,强度包络线与莫尔圆最先相切的是最大与最小主应力所围成的应力圆,因此发生破坏也必然与σ1和σ3有关。如果分析的边坡为平面形式,则破坏强度只与σ1和σ2有关。

图2 空间应力状态下的莫尔圆

1.2 安全系数取值的讨论

力是矢量,所以由主应力构成的安全系数应该含有方向参数。因此,很多学者提出基于矢量法的安全系数定义[6,8-12],即将安全系数视为与方向有关的量。上述文献中的滑动方向都为已知的或潜在的,所以通过力的分解便可得到滑动方向上抗力与下滑力之比。如果潜在滑动方向未知,显然给计算带来困难。点安全系数法中,当最小安全系数小于1时,按照摩尔-库伦准则评价土体材料已不足以抵抗破坏,但并不是所有安全系数小于1的岩土区域就要发生失稳,这与失稳区的边界效应有关。此外,最小安全系数的单元体不一定代表滑体的主滑方向,即点安全系数法中识别的破坏单元只是边坡失稳的必要非充分条件。

1.3 整体安全系数的定义

鉴于以上的考虑,每个单元体的安全系数都是局部的,并不足以表征边坡的整体稳定能力。因此,在边坡整体安全系数的定义中引入滑动面倾角的权重,即将整体安全系数视为与滑动面倾角大小有关,建立全局与局部的关系。由此,整体安全系数Fs表述为

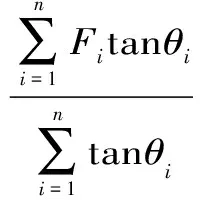
(2)

式中,Fi为潜在滑动面上各点的安全系数；tanθi为计算单元滑动面与水平线夹角的正切值,可以描述为滑动面计算单元对整体安全系数的贡献率。n为潜在滑动面上的计算单元总数。

2 简单算例验证

以文献[13]提供的算例核验点安全系数法的可靠性,几何模型及材质属性参见文献[13]。采用有限元强度折减法和点安全系数法计算边坡的稳定性,计算结果见图3。提取潜在滑动面上每个点的安全系数,按式(2)得到的整体安全系数Fs为2.83,强度折减法得到的安全系数F为2.9,两者基本一致。从图3可知,2种方法识别的边坡滑动面位置和安全系数值都基本相近,但点安全系数法的结果略小,较强度折减法低2.5%。图3b显示边坡滑动面近似为圆弧状,与图3a的等效塑性应变区形状基本一致,说明点安全系数法能够反映边坡的失稳体。

图3 不同方法计算的边坡滑动面分布

文献[6]提供了ACADS发布的经典算例,以此校核点安全系数法的合理性。有限元强度折减法和整体安全系数的结果分别为F=1.0和Fs=0.92(见图4)。对比发现,2种方法计算的滑动面形状和位置基本一致。同样,点安全系数结果略小,偏差为8.0%。文献[6]中Donald计算的安全系数为1.0,Fredlund计算的结果为0.99。可见,点安全系数法结果相比其他方法也要偏于保守[6]。上述2个算例的结果表明,点安全系数法识别的失稳区与强度折减法基本一致,而采用整体安全系数来评价边坡稳定性则要偏于安全,具备工程应用性。

图4 不同方法计算的边坡滑动面分布

3 工程实例分析

某工程为三级基坑,基坑长20 m,上层为素填土,埋深3.7 m；下层为粉土,距坑底2.8 m。素填土参数：容重γ=20 kN/m3,粘聚力c=3 kPa,内摩擦角φ=10°,泊松比μ=0.2,弹性模量E=4 MPa。粉土参数：容重γ=20 kN/m3,粘聚力c=35 kPa,内摩擦角φ=18°,泊松比μ=0.3,弹性模量E=10 MPa。按照文献[14]设置边坡几何尺度及边界条件,进行三维静力分析,得到的最小安全系数分布见图5。

图5 最小安全系数分布

从图5可知,边坡不稳定的区域集中在坡脚,与前期的勘察验算结论相符。失稳区最外侧就是潜在的滑动面,按式(2)计算的整体安全系数Fs约为1.28,与勘查报告计算结果1.39相比仍偏保守。综合推断,边坡失稳最先从坡脚开始,而后逐渐向上扩展,初始静力条件下滑动面虽未贯通至坡顶,但不安全的区域已发展到坡面,构成了贯通区。施工中,在基坑底部四周砌筑临时挡土墙以防止坡脚失稳,这一保护措施与点安全系数法的评价结论相符。

图6是边坡中截面位置的切应力等值线分布。从图6可知,坡脚处的等值线分布较为密集,呈现应力集中，这与坡面到坡脚的几何突变有关,说明边坡因应力集中而出现坡脚失稳,与点安全系数法识别的失稳区位置相同,证明了该法的合理性。底层粉土因滑动促使抗剪强度不足以抵抗上部坡体自重产生的剪切力,所以坡脚是边坡开挖过程中需注意的薄弱位置。

图6 边坡xy方向切应力等值线分布(单位：Pa)

综合以上算例结果可以得出,基于滑动面倾角权重的边坡稳定性评价方法是合理的,具备工程实用性。一般情况下,有限元强度折减法将粘聚力和内摩擦角的折减系数取为同一值以简化计算,而实际上这2个参数的衰减程度是不同的,对边坡稳定性的贡献自然也不同,文献[14]已有论述,并提出了双折减参数的概念。点安全系数法巧妙地回避了岩土强度指标衰减规律不同的特点,直接通过应力计算获得每个单元体的安全系数,并通过加权得到边坡的整体安全系数,工程实用性高。此外,点安全系数法的计算主要采用弹性理论,故安全性评价结果也更安全。

4 结 语

本文基于滑动面倾角权重的整体点安全系数法评价边坡稳定性,得到以下几点结论：

(1)计算单元的点安全系数只与单元体的大小主应力及材料强度指标有关。通过滑动面倾角建立边坡整体安全系数与滑动面上每个点安全系数的联系,与不同算例的强度折减法结果吻合较好,验证了整体安全系数的可靠性。

(2)加权整体安全系数需搜索边坡潜在滑动面上每个点的安全系数,通过计算单元体最小安全系数并构成连续贯通的区域,才能形成失稳区,即剪出口应位于坡顶、坡面或坡脚,而失稳区的最外边缘即为潜在滑动面。如果计算单元的最小安全系数小于1、连续、自行封闭,或与固定边界封闭,或无剪出口,坡体也会因边界约束而稳定。

(3)边坡整体安全系数偏小主要源于弹性理论,评价结论偏于保守。与传统极限平衡法相比,该方法省略了潜在滑动面的确定,工程实例也证实了结果的可靠性。对于异形边坡或多种外荷载(如地震、地下水渗流等)作用下的边坡,采用该法也可得到边坡的安全系数,具备工程适用性。

[1]郑颖人, 赵尚毅. 边(滑)坡工程设计中安全系数的讨论[J]. 岩石力学与工程学报, 2006, 25(9)： 1937- 1940．

[2]郑宏, 田斌, 刘德富. 关于有限元边坡稳定性分析中安全系数的定义问题[J]. 岩石力学与工程学报, 2005, 24(13)： 2225- 2230．

[3]马健全, 王念秦, 张新社. 基于点稳定系数法的斜坡稳定性分析[J]. 吉林大学学报： 地球科学版, 2015, 45(2)： 533- 540．

[4]郑文堂. 基于FLAC3D的强度折减法和点安全系数法对比[J]. 水利与建筑工程学报, 2010, 8(4)： 54- 57．

[5]卢玉林, 薄景山, 王丽, 等. 渗流地震双重工况下砂土边坡稳定性解析计算[J]. 应用力学学报, 2016, 33(5)： 772- 778．

[6]刘艳章, 葛修润, 李春光, 等. 基于矢量法安全系数的边坡与坝基稳定分析[J]. 岩石力学与工程学报, 2007, 26(10)： 2130- 2140．

[7]杨洁, 杨上清, 肖盛燮. 强震边坡动力响应及安全系数计算[J]. 重庆交通大学学报： 自然科学版, 2011, 30(2)： 277- 281．

[8]杨涛, 周德培, 马惠民, 等. 滑坡稳定性分析的点安全系数法[J]. 岩土力学, 2010, 31(3)： 971- 975．

[9]杨涛, 刘涌江, 杨兵, 等. 应用点安全系数分析基坑边坡三维稳定性[J]. 岩土力学, 2014, 35(3)： 1756- 1761．

[10]王国体. 边坡稳定和滑坡分析应力状态方法[M]. 北京： 科学出版社, 2012．

[11]徐芝纶. 弹性力学简明教程[M]. 北京： 高等教育出版社, 2002．

[12]邵龙潭, 李红军. 土工结构稳定分析—有限元极限平衡法及其应用[M]. 北京： 科学出版社,2011．

[13]赖永标, 胡仁喜, 黄书珍. ANSYS11.0土木工程有限元分析典型范例[M]. 北京： 电子工业出版社, 2007．

[14]郑颖人, 赵尚毅, 李安洪, 等. 有限元极限分析法及其在边坡中的应用[M]. 北京： 人民交通出版社, 2011．

(责任编辑 杨 健)

Slope Stability Evaluation Based on the Weight of Sliding Inclination Angle

LU Yulin1,2, BO Jingshan1,2, CHEN Xiaoran3, WANG Li1
(1. Department of Disaster Prevention Engineering, Institute of Disaster Prevention, Beijing 101601, China;2. Institute of Engineering Mechanics, China Earthquake Administration, Harbin 150080, Heilongjiang, China;3. China North Industries Norengeo Ltd., Shijiazhuang 050011, Hebei, China)

Based on the advantage of point safety factor method, the stress states of calculated elements are obtained by the elastic mechanics, and then the safety factor of slope is computed by Mohr-coulomb theory. The potential sliding surface of slope is can be recognized after the determination of minimum safety factor. The relationship between the minimum safety factor and the general safety factor is established by taking the sliding surface inclination as weight, therefore the slope stability is evaluated by general safety factor．

slope stability; general safety factor; point safety factor method; slip inclination angle

2016- 06-30

廊坊市科学技术研究自筹经费项目(2016011057)；中央高校基本科研业务费专项资金项目(ZY20150203)

卢玉林(1983—),男,北京人,讲师,博士研究生,主要从事岩土边坡稳定性研究工作．

TU457

A

0559- 9342(2017)05- 0033- 04