应用聚类分析和数值模拟技术处理渗透率方法

姚君波，袁 立，崔龙涛，何 芬，陈存良

（中海石油(中国)有限公司天津分公司，天津 300452）

不论是在油田生产历史拟合还是生产指标预测中，渗透率在数值模拟中是非常重要的地质参数。在历史拟合中，水平与垂直渗透率的精确度直接影响到单井和全区的产油量和产水量的拟合程度。在预测压力分布、水的突破时间及剩余油分布时，渗透率存在误差会影响油田开发方案的前期部署、中后期调整，甚至可能出现重大失误，造成严重的经济损失。

随着油藏埋深的增加，受地层压力增大的影响，垂向渗透率往往比横向渗透率减小更快，储层渗透率的各向异性会表现得更为明显[1-2]。在油田开发研究中，很难获取各个方向的渗透率数据，很多地质建模模拟的渗透率只有数值而没有方向，然而在进行数值模拟的时候，需要三个方向渗透率。为此，现在比较普遍的方法是利用经验公式对模型三个方向的渗透率数据赋值，假设油藏各水平裂缝方向皆一致，水平渗透率与网格模型数值相同，垂直渗透率等于模型渗透率的值乘以0.1。这种方法缺乏科学性和准确性，只是粗略地估计各向异性上的渗透率。为了建立相对准确的油气水三相渗流运动模型，本文针对 petrel建模软件导出的渗透率数据体，运用ward聚类分析方法进行处理[3]，再利用三维空间几何运算，推导出角度转换公式，从而把渗透率值分解到 x、y、z三个方向，大大提高了数值模拟的准确度，从而为油田的开发方案制定提供有力依据。

1 实验设计

1.1 求取数据间距离

在渗透率变化不是非常剧烈的情况下,采用欧氏距离计算公式分析各个数据点之间的亲疏程度，并依此进行系统聚类分析，在选用method分析时运用ward法进行聚类。对样本聚类(Q型聚类)一般采用距离系数计量。距离系数越小则样品间的距离越小，样品差异就越小。距离较远的点应属于不同的类[4-5]。由于基于方差分析的 Ward法要求样品间的距离必须是欧氏距离，所以此次研究采用欧氏距离公式进行计算。

1.2 聚类方法的选择

Ward最小离差平方和法是根据方差分析的原理得到的[6-7]。ward离差平方和法是一种特殊的聚类方法，更符合油气田开发中地质规律对数据的分类。计算时首先将离差平方和最小的数据合并成一类，使得类内离差平方和增加最小，直至所有的样本聚成一类为止。Ward方法总是聚类导致的类内离差平方和增量最小，而类间离差平方和应当较大，这样就可以获得在外界条件变化处于正常范围内的数据聚类中心。

1.3 实验模型建立及流程

从 petrel建模软件中导出的基础数据中有“PERMEABILITY”关键字，关键字下面包含的是建模导出的渗透率数据体，每个数值表示的是每个网格中的渗透率值，但是它没有方向性。实际油藏中它应该具有方向性（permx、permy、permz）。目前在进行油藏数值模拟时的大部分做法是人为赋值后进行运算，如使 permx=perm，permy=perm，permz=1/10perm。这是一种经验赋值，缺乏准确性，对油田开发方案的准确制定有一定的影响。

将地下油层的情况用三维网格进行模拟，网格中的渗透率数值是用三维坐标来定位的，不同的网格具有不同的坐标值和网格值，根据聚类分析算法，搜索范围包括九方格体中的27个网格值，并分出两类，渗透率值和中心点相近的为 a类，其他值为 b类。找出中心点坐标指向a类中除中心点以外其他点的重心，就可以确定渗透率的方向了，而这个方向上的渗透率值的大小可用加权平均法来求取，然后通过正弦、余弦公式分别求出分解到各坐标方向上的渗透率值。将九方格体依次沿三个坐标方向移动，并重复上面的步骤，可以求出每一个网格三个方向的渗透率值（permx、permy、permz）。相比较传统的人为矩阵赋值运算，此算法融入了数学地质思想，在数据变化速度较为稳定的条件下，更接近实际地质情况。

1.4 实验数据准备

为了较真实地模拟地下油藏情况，建立了一套渗透率数据（表1），表中每列的数据类型必须相同，每个渗透率数值分别位于该网格左上角，以九宫格为一个单元进行一次聚类分析，运行结束后，中心自动移到下一个网格，移动顺序为x、y、z方向。考虑到考察的样本一般都有不同的量纲，为了使不同量纲、不同取值范围的数据能够放在一起进行比较，先对数据进行标准化变换，即数据矩阵中每列数据的平均值为0，方差为1。实验初始数据和标准化后的数据如表1。

1.5 实验数据处理

表1 实验数据的标准化处理

采用欧氏距离公式计算标准化变换后的变量间的Euclidean 距离，计算过程由SPSS统计分析软件实现，并用距离相似系数矩阵表示。运用SPSS软件进行聚类分析，在给定聚类分类个数后，选用method分析时运用 ward法进行分类[8-12]。当计算出了距离矩阵或相关矩阵后，为了比较直观地看出样本或变量间的关系，常用谱系图来表示分类结果（图 1）。从谱系图上可以清楚地看出，B230、B330、B220、C33-1为一类，其余点为一类，这与原始渗透率数据分类完全吻合。因此可以得出，聚类分析可以在不偏离原有渗透率值网格分布规律下较为安全稳定地对数据进行聚类。

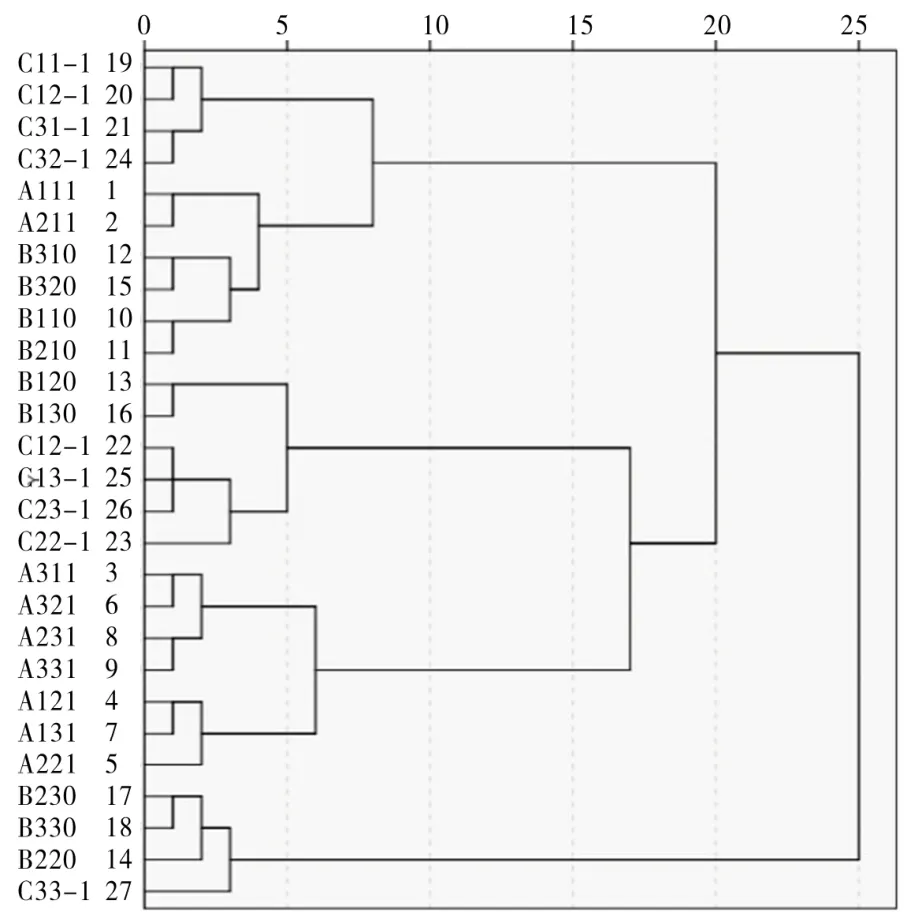
图1 分类结果谱系图

2 应用空间几何求取三维渗透率值

2.1 求取主方向渗透率值的大小

通过聚类分析方法找出符合条件的那一类渗透率值之后，下一步求取渗透率的主方向以及主方向上的渗透率值的大小。通过聚类方法找出了与中心值属于同一类的 个值，利用算术平均值的方法求取主方向的渗透率值[13-16]。

2.2 求取渗透率的主方向

已知符合这一类渗透率值的三个点在空间上形成一个三角形的面，又已知这三个点的空间坐标，先用中点公式求出各边中点坐标，再用定比内分点公式求出重心M（x0、y0、z0）的数据。

求取出重心点的坐标后，由中心指向重心的方向为渗透率主方向。如果这一类点的个数为4，可通过求取质心坐标来求取渗透率方向，如果这一类点的个数超过 4，则倾角和方位角为这几个点倾角和方位角的加权平均值，从而确定了渗透率的主方向。

2.3 通过三维角度变换求取三维空间渗透率

将三维空间中渗透率的主方向分别投影到到xz和yz平面上，根据中心点和重心点M的三维空间坐标确定θyz、θxz（θyz、θxz分别为投影到面上的线与坐标轴y和z的夹角）；通过几何运算，可以得到一个网格上的渗透率值，并分别计算出三个坐标方向上的渗透率值。随后可进行下一个网格的渗透率计算，直至将研究区所有网格计算完毕。

3 实例应用

A区块油藏被两条相互交错的具有封闭性质的断层阻隔，属于断层控制的断块油气藏，储层非均质性强。储层向东南方向下倾，倾角约为5.8°，层内存在夹层。储层渗透率的变化主要有两种类型，即反韵律型和复合韵律型。反韵律型表现为高孔隙度和高渗透率段分布于砂体顶部，向上孔隙度和渗透率逐渐增大，渗透率值由 180.6×10-3μm2变为387.0×10-3μm2，为向上变大的反韵律。基于地质上的认识，将经过本次研究方法处理后的渗透率模型与未处理过的渗透率模型导入到数值模拟中进行计算对比，选取C11井的压力以及含水率拟合情况进行对比（图2～图5）。通过对比发现，渗透率值经过本次研究方法处理后，油藏压力和含水率拟合准确度明显提高，计算结果能够更加真实地反应出地下油藏情况，为A油田后续开发方案制定提供了有力的保障。

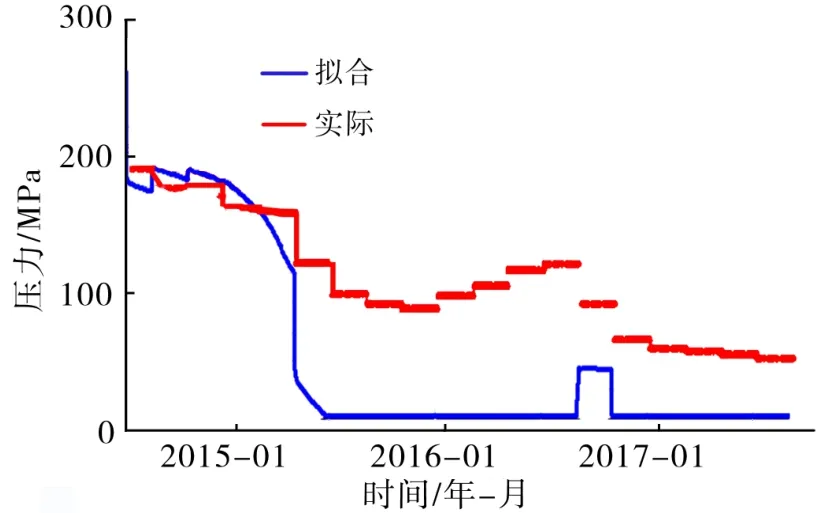
图2 渗透率处理前C11井实际压力与拟合压力对比

4 结论

（1）在聚类分析方法中找到了适用于处理渗透率三维空间值的数学模型。

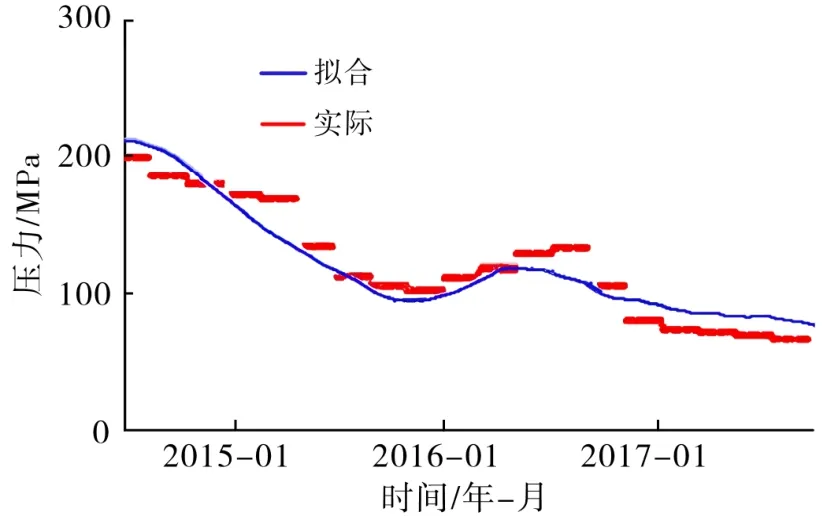
图3 渗透率处理后C11井实际压力与拟合压力对比

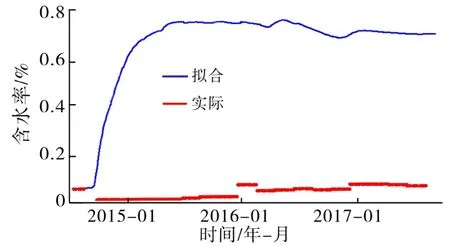
图4 渗透率处理前C11井实际含水与拟合含水对比

图5 渗透率处理后C11井实际含水与拟合含水对比

（2）利用标准化后的模型可以求取各个数据样本之间的欧氏距离，即相似度差异，然后通过ward离差平方和的聚类方法，对数据进行聚类，处理结果更符合实际地质情况。

（3）通过聚类分析模型与三维空间几何计算相结合，可以求解出油藏三维空间渗透率值的大小和方向。

（4）本次研究方法在油田实际应用中已经得到很好的验证，与现在的经验方法相比，大大提高了准确性，计算结果更加符合实际地质情况。