岩心介电特性及饱和度模型研究

李君建 ，柯式镇 ，尹成芳 ，康正明 ，邹德鹏 ，马雪瑞

（1.中国石油大学（北京）地球物理与信息工程学院，北京 102249；2.中国石油大学（北京）油气资源与探测国家重点实验室；3. 中国石油大学（北京）图书馆）

在石油勘探开发中，电法测井是油气评价的先导，Archie公式使电阻率成为定量评价含油饱和度的重要参数[1]。此外，还有一个非常有意义的参数，那就是介电常数ε，用于表征介质极化强度；通常使用的是相对介电常数ε!，二者关系为ε!= ε/ε"（ε"是空气的介电常数）。研究表明，水的相对介电常数要比岩石骨架的相对介电常数高一个数量级。20世纪60年代，介电测井就已经应运而生[2]，但由于应用效果不是很理想，所以没有得到广泛的推广和发展。随着油气勘探开发难度的日益加大，人们重新重视对介电测井方法的研究，斯伦贝谢推出了介电扫描测井（ADT），在矿化度未知的情况下，结合密度等其他测井技术，在较浅油藏、稠油油藏、薄互层等地层评价中具有良好的应用效果[3-12]。目前介电测井技术主要由国外公司掌握，我国急需开展这方面技术的研究应用。

1 岩心介电特性影响因素实验分析

1.1 实验参数

本次实验采用人造砂岩岩心，岩心由玻璃微珠胶结压制而成，将岩心加工成直径为38 mm、厚度为3 mm的薄片，各项参数如表1。实验采用水驱空气的方式改变岩心的含水饱和度，每轮实验分别向岩心中滴加蒸馏水和0.5%、1.5%、2.5%质量分数的NaCl溶液，直至岩心质量不再增加后，采用真空加压的方式改变饱和度，对岩心进行相对介电常数的测量，测量频率为20 MHz～1GHz。

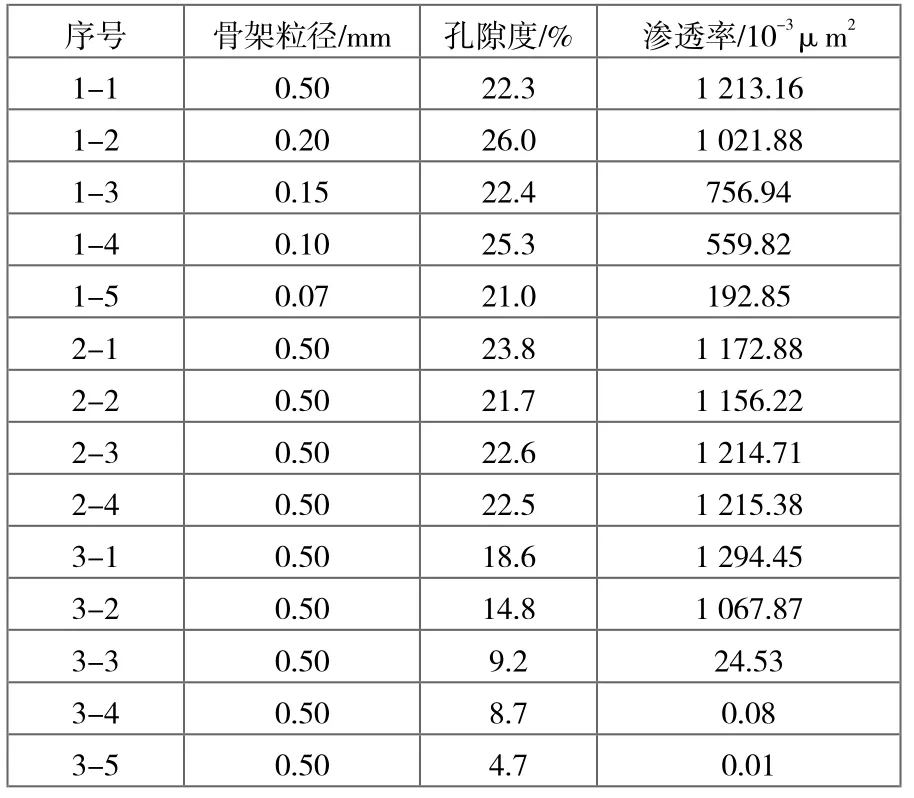
表1 岩心基本参数

1.2 岩石骨架的相对介电常数

实验发现，干燥岩心的相对介电常数基本没有频散。对干燥的岩心来说，岩心的相对介电常数主要来自岩心骨架颗粒和孔隙中空气的贡献，二者均不导电且是非极性分子，岩心中只存在电子极化和原子极化，故岩心的相对介电常数基本不随频率的变化而变化。对于孔隙度不同的干燥岩心，其相对介电常数随孔隙度变化的关系如图 1，可以看出二者有很好的线性关系。当孔隙度为0时，干燥岩心的相对介电常数即为岩心骨架相对介电常数。本次实验岩心骨架相对介电常数约为5.4。

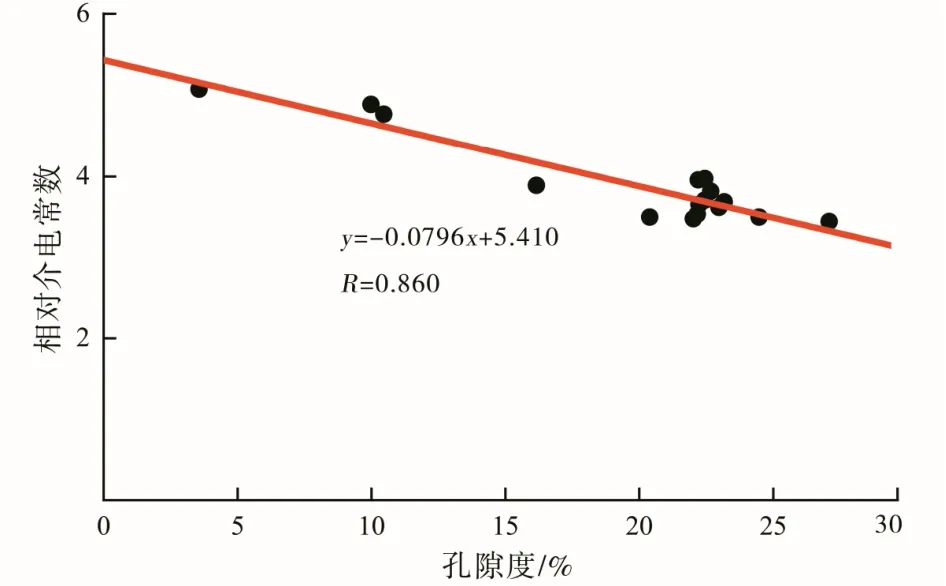
图1 岩心相对介电常数与孔隙度的关系

1.3 饱和度对介电特性的影响

图2是编号 1-3岩心相对介电常数随饱和度变化曲线，其中饱和溶液分别为蒸馏水、矿化度为2.5%的NaCl 溶液，从中可以看出，随着饱和度的增加，相对介电常数增加。另外，干样即含水饱和度为0时岩样几乎不频散，同时，含蒸馏水岩样的相对介电常数也不随频率变化，这与理论上纯水的介电常数在频率为 10 MHz以前都没有频散现象[5]一致。这说明蒸馏水非常纯净，没有任何杂质和离子，当频率增加时，蒸馏水与岩石界面处也不会存在电荷堆积的情况，也就不存在界面极化现象，因此，含蒸馏水岩样不频散。

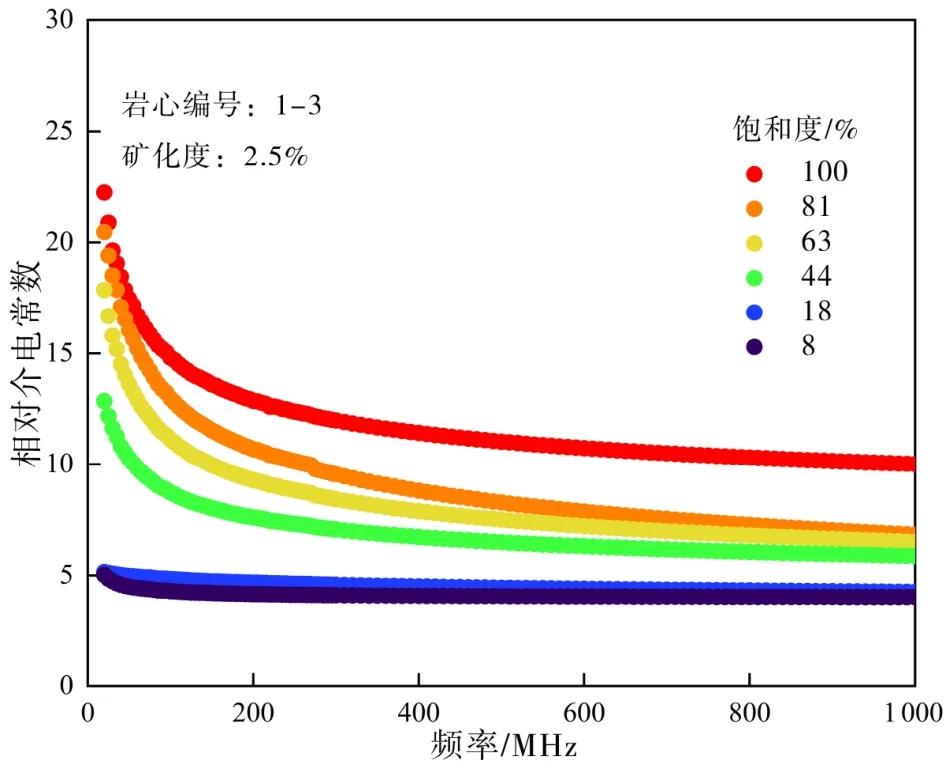
图2 饱和度对相对介电常数的影响

1.4 矿化度对介电特性的影响

由图3可以看出，随着矿化度的增高，岩样的相对介电常数增大。低频时，矿化度越高，频散越明显，当频率大于 600 MHz，不论哪种矿化度均几乎不存在频散现象。根据双水理论，岩石孔隙中的水有束缚水和自由水两种存在形式，由于岩石骨架带有一些电荷，且水是极性分子，因此骨架表面会吸附一层水膜，这部分水称为束缚水；孔隙中未被骨架吸附的水则称为自由水。自由水的相对介电常数约为 80，而在电场作用下，束缚水不再发生转向极化，所以束缚水相对介电常数远小于80，仅为6～8。现在孔隙中液体为 NaCl 溶液，存在大量氯离子和钠离子，这些离子比极性水分子更易被骨架吸附，从而与束缚水分子发生离子交换，矿化度越高，离子越多，交换出的束缚水亦越多，因而整个孔隙体系中束缚水比例降低、自由水比例升高，进而造成相对介电常数增大。低频时，由于界面极化的影响，矿化度越高，离子越多，离子在界面堆积程度也越高，从而增强了界面极化。所以矿化度越高、频率越低，频散越明显。高频时，岩样的频散程度很低，矿化度对相对介电常数的影响较小。

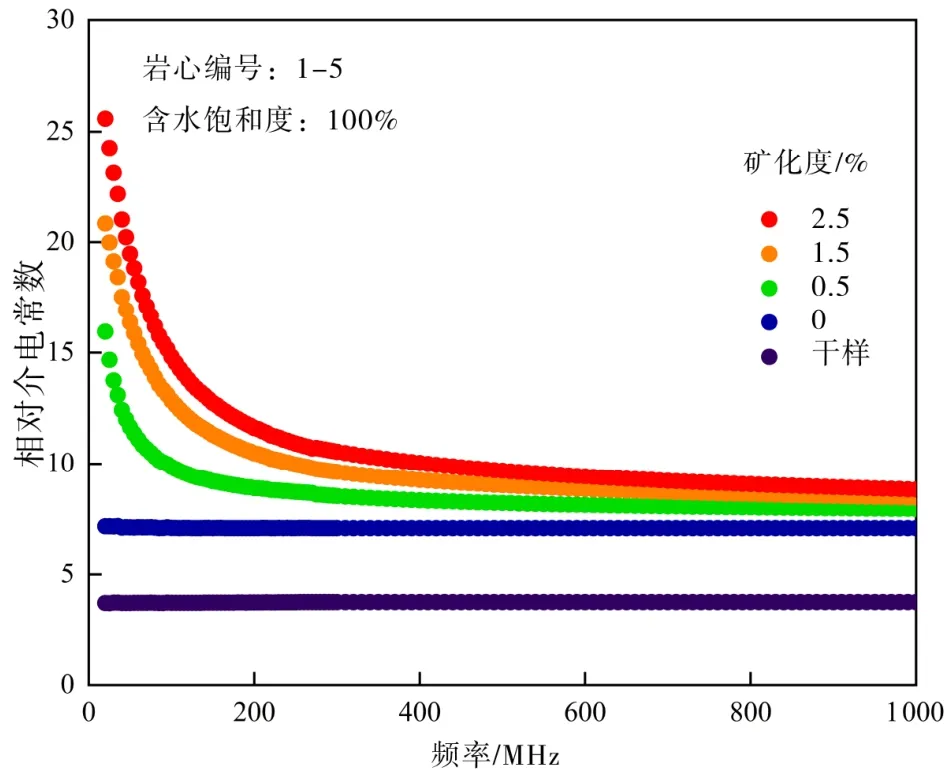
图3 矿化度对相对介电常数的影响

1.5 孔隙度对介电特性的影响

岩心1-2、2-1、1-5的孔隙度分别为26.0%，23.8%，21.0%。由图4可以看出，随着孔隙度的增加，相对介电常数增加。当孔隙度增加时，孔隙中的自由水相对增多，发生转向极化的概率也相对增加，故而造成相对介电常数增大。

2 多频介电解释模型

矿化水在岩石的介电特性中起着非常重要的作用。由Debye公式可知[9]，当水中含有离子时，其复介电常数可以表示为：

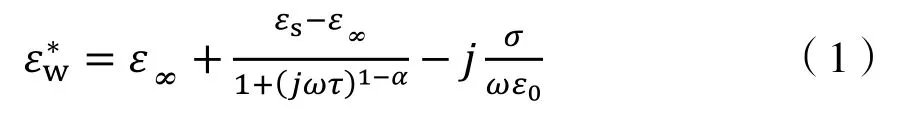
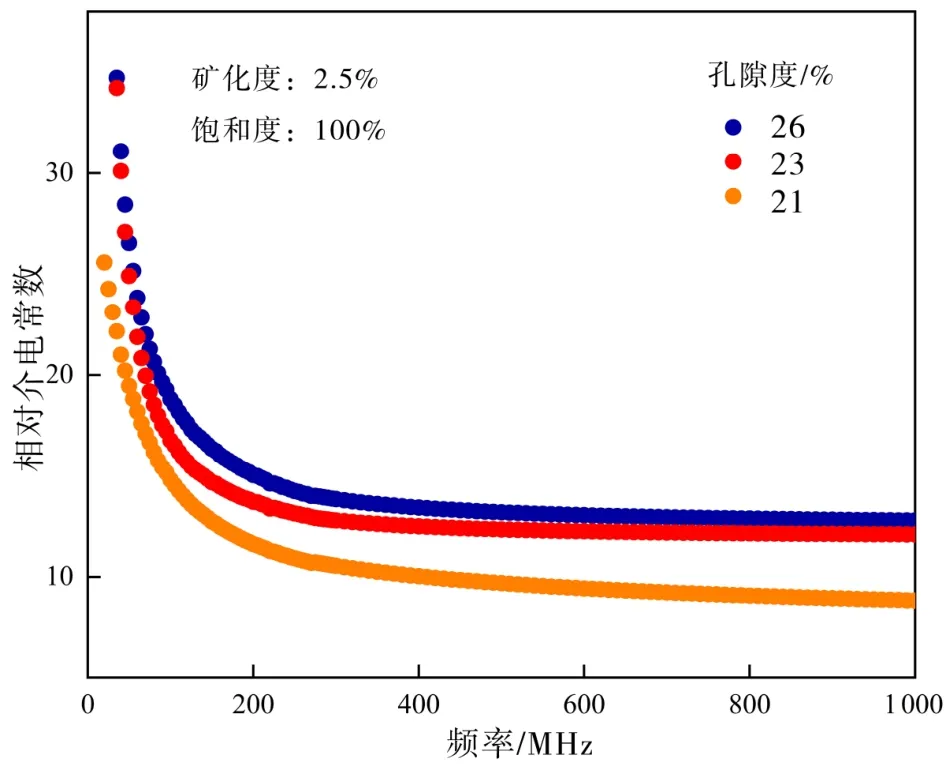
图4 孔隙度对相对介电常数的影响

一些专家学者为了描述水的介电特性，做了很多研究。1977年，Klein和Swift在Stogryn研究结果的基础上，结合之前的实验数据，进一步对低频段数据进行拟合，修正了Stogryn提出的公式[10]。前人给出了不少关于单一频率的介电解释模型，对比各模型与实验数据（图 5）发现，实验数据和Lichtenecker模型吻合较好。

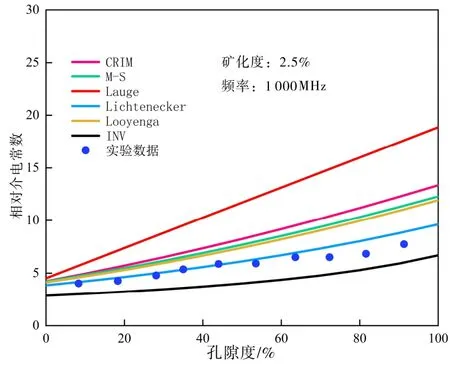
图5 实验数据与各模型模拟结果对比

对于多频的介电解释模型，仅用岩石各部分介电常数的加权和是不能满足要求的。Maxwell-Garnett 是等效介质理论混合公式研究的先驱，主要是对多种物质颗粒随机混合而成的混合介质，研究其有效介电常数，但对于岩石介电常数研究来讲，不论是导电相（水）还是绝缘相（骨架、油气）都是连续的，因此，选任何任何一种相作为背景相都是与现实不符的。基于介电测量数据与 Lichtenecker模型吻合较好，将 Lichtenecker 模型作为混合公式的背景，再考虑到颗粒间的多重散射作用影响，假设混合介质中均为球形颗粒物质紧密接触而形成，演化出适用于多频介电测井频率范围的介电解释混合模型：

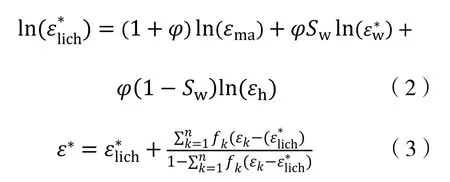
式中：φ为孔隙度，%；=w为含水饱和度，%；分别为骨架、水、空气的相对介电常数，εh=1，εma由干岩样的相对介电常数计算得到，为5.4；ε∗为岩石复介电常数；为以Lichtenecker模型为背景的复介电常数；εk为第k个包裹相，对应的体积分数为fk；对于含有油气的纯砂岩来讲，B=3。

表2是实验数据和利用新模型（公式2和公式3）计算的数据对比。以1-3号岩心为例，当岩心饱和1.5%NaCl溶液时，选取高中低含水饱和度下不同频率的相对介电常数与计算值进行对比。综合所有数据来看，模型计算值与实验测量值相对误差在5%以内，模型计算值精度较高，基本能够满足测井解释实际需求。

3 结论

通过对人造砂岩介电常数的测量，得到了介电常数与饱和度、矿化度、孔隙度之间的关系；基于Lichtenecker模型，并结合 Maxwell-Garnett等效介质理论，给出了适用于多种频率的介电混合解释模型。

（1）对于干燥的岩石，介电常数基本不发生频散；随着含水饱和度的升高，岩心相对介电常数增大，介电频散程度越来越大；在各个频率点下，岩石相对介电常数与含水饱和度有很好的线性关系。

（2）当孔隙水中无离子时，岩石基本不发生介电频散。随着矿化度的升高，岩石的介电频散程度越来越大，对高频处的影响较低频处小得多，但矿化度对高频介电常数依然有影响。

（3）岩心相对介电常数随孔隙度的增大而频散程度增大，在各个频率点下，岩心相对介电常数与孔隙度有良好的线性关系。

（4）适用于多种频率的新介电混合模型的实例计算结果与实验数据符合较好，精度较高，能够满足实际解释需求。