交流电机谐波电动势分布因数出现负值的分析研究*
龙 飞,蒋 伟,徐敏伟,莫岳平
(1.扬州光电产品检测中心,江苏 扬州 225009;2.扬州大学 水利与能源动力工程学院,江苏 扬州 225002)
0 引 言
交流电机产生的谐波感应电动势,注入公用电网后,会给电网和接在该电网的其他用电设备的运行带来不良影响甚至危害[1]。因此在设计交流电机时,应当根据国标中公用电网谐波电压限值的要求[2],把感应电动势中的谐波含量限制在一定范围内。采用短距线圈和分布绕组能有效地改善电动势波形、抑制谐波分量,故一般的交流绕组大多采用短距、分布绕组。谐波电动势绕组因数kwv=kpv×kdv,文献[3]中已详细论证了谐波节距因数kpv,因此,本研究将重点探讨绕组的另一个因数:谐波电动势分布因数kdv(研究范围限定为三相整数槽绕组)。
国内外学者研究分布绕组分布因数的方法主要有两类:代数法和几何法[4-11]。代数法适应面广,但缺点是不够直观。几何法的优点是直观,目前主要针对基波电动势,KOSTENKO M、CHAPMAN S J、UMANS S D、汤蕴璆提出的基波公式可以统一表述为kd1=(sin(qα1/2))/
(qsin(α1/2)),而针对谐波电动势尚缺乏深入的研究,现有谐波分布因数kdv公式均是用vα1(=αv)直接替换基波公式中的α1衍生而来,比如KOSTENKO M、汤蕴璆给出的谐波公式均可以表述为kdv=(sin(vqα1/2))/(qsin(vα1/2))。由于αv=vα1,角的范围简单扩大带来了下列两种基波计算不会出现而谐波分布因数kdv和电动势有效值计算会出现的负值问题:
(1)(αv/2)=(vα1/2)∈((2k1+1)π,(2k1+2)π)且(qαv/2)=(vqα1/2)∉((2k2+1)π,(2k2+2)π)(k1,k2=0,1,2,…)
(2)(αv/2)=(vα1/2)∉((2k1′+1)π,(2k1′+2)π)且(qαv/2)=(vqα1/2)∈((2k2′+1)π,(2k2′+2)π)(k1′,k2′=0,1,2,…)
例如当αv=vα1=(2k3+1)π(k3=0,1,2,…)时,根据现有谐波公式计算结果为kdv=(sin(qπ/2))/q,当q=3,7,11…时为负值,这其中:αv=3π,7π,11π…属于第(1)种情况,αv=π,5π,9π…属于第(2)种情况。
针对这一问题,本文提出应用极相组q个等相位差非零相量合成的新理论,提出新的谐波电动势分布因数公式。
1 分布绕组谐波合成电动势相量模型
1.1 绕组分析常用基本量
(1)
(2)
式中:p,τ—基波的极对数、极距;q—每极每相槽数,本研究中q为整数;m—相数,本研究中m=3;Z1—定子槽数。
1.2 谐波磁场的性质
极对数关系:
pv=vp
(3)

(4)
式中:pv,τv—v次谐波的极对数、极距。
主极磁场仅含有奇次空间谐波,即v=1,3,5,……。
1.3 相合成电动势
两个线圈的基波合成节距用电角度表示,即:
(5)
式中:y—线圈基波合成节距,用槽数表示。
v次谐波的合成节距:
(6)
为论述方便,笔者以A相为例,把N极下的某个极相组(例如双层叠绕组的A相带)和S极下的对应极相组(例如双层叠绕组的X相带)对应导体的槽距定义为“极相组合成节距yp”,以区别于“线圈合成节距y”。
1.3.1 双层叠绕组
(7)
(8)
式中:k=1,2,……,p。

(9)
1.3.2 双层波绕组

(10)
1.4 极相组合成电动势
基波相邻两槽间的电角度为:
(11)
v次谐波相邻两槽间的电角度为:
(12)
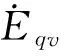

(13)
2 极相组谐波电动势相量合成分析
2.1 相邻两槽间电角度αv的区间划分
由(11)式知,0<α1=π/(mq)≤π(这里m≥1,q≥1,且m、q均为整数),因此根据式(12)有:0<αv=vα1≤vπ。值得注意的是,v的奇数性使得αv在(0,vπ]内存在下列3类奇点:
(1)周角的全部点:若奇数v能被mq整除,则v/(mq)必不为偶数,因此αv=vπ/(mq)≠(2k+2)π,即αv-2kπ≠2π,k=0,1,2,…且2k+3≤v;
(2)劣角的部分点:αv≠[2k+(2l1/q)]π,即αv-2kπ≠(2l1/q)π,l1=1,2,3,…且q>2l1;k=0,1,2,…且2k+1≤v(证明见2.3.1节情形四);
(3)优角的部分点:αv≠[2k+2-(2l2/q)]π,即αv-2kπ≠2π-(2l2/q)π,l2=1,2,3,…且q>2l2;k=0,1,2,…且2k+3≤v(证明类同于劣角,从略)。
因此,αv在(0,vπ]内除去上述三类奇点外的任何区间均有可能。随(αv-2kπ)与π大小关系的不同,极相组q个线圈v次谐波电动势相量在相量图中按平移求和法则的走向亦不同。为此,笔者把(0,vπ]划分为3部分区间(或点),即:
(1)劣角(除去部分奇点):2kπ<αv<(2k+1)π,即0<αv-2kπ<π,k=0,1,2,…且2k+1≤v;
(2)平角:αv=(2k+1)π,即αv-2kπ=π,k=0,1,2,…且2k+1≤v;
(3)优角(除去部分奇点):(2k+1)π<αv<(2k+2)π,即π<αv-2kπ<2π,k=0,1,2,…且2k+3≤v;
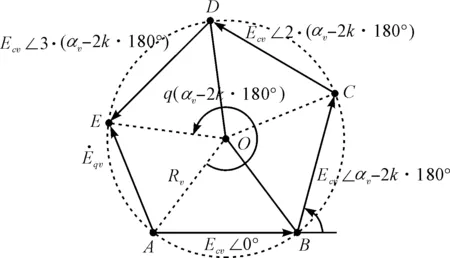
按首尾相连原则作出的相量示意图如图1所示。
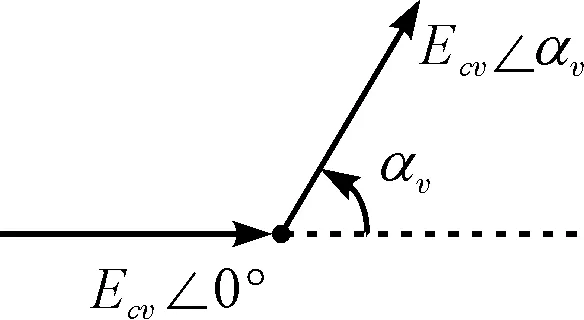
(a)2kπ<αv<(2k+1)π情形,k=0,1,2,…且2k+1≤v
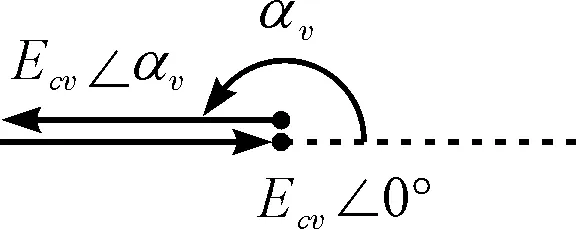
(b)αv=(2k+1)π情形,k=0,1,2,…且2k+1≤v

(c)(2k+1)π<αv<(2k+2)π情形,k=0,1,2,…且2k+3≤v图1 v次谐波相邻两槽间电角度的区间划分
2.2 极相组相量合成新理论
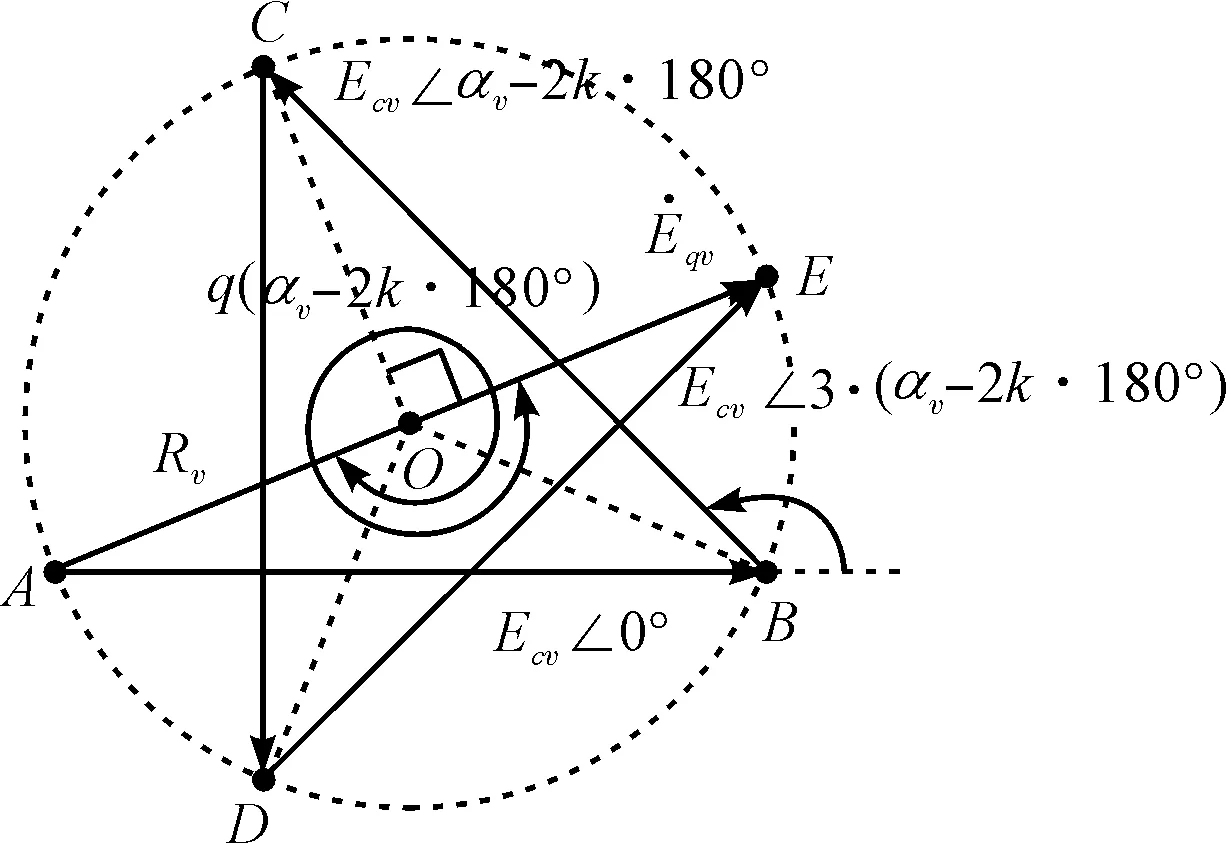
国内外学者之前的理论是“极相组q个电动势相量大小相等,又依次移过α1电角度,因此相加之后构成了正多边形的一部分,而正多边形必有外接圆”,这可以从360°/α1=360°/(180°/(mq))=2mq恰好为整数边得到解释。
但是,q个相量两两之间相位差从基波α1=180°/(mq)扩大到v次谐波αv=v·180°/(mq)后,v的奇数性造成了360°/(v·180°/(mq))不能确保为整数,即不一定能构成正多边形。
笔者提出如下结论:q个非零相量,若每个相量的相位彼此均相差αv角,αv-2kπ∈(0,2π)且αv-2kπ≠
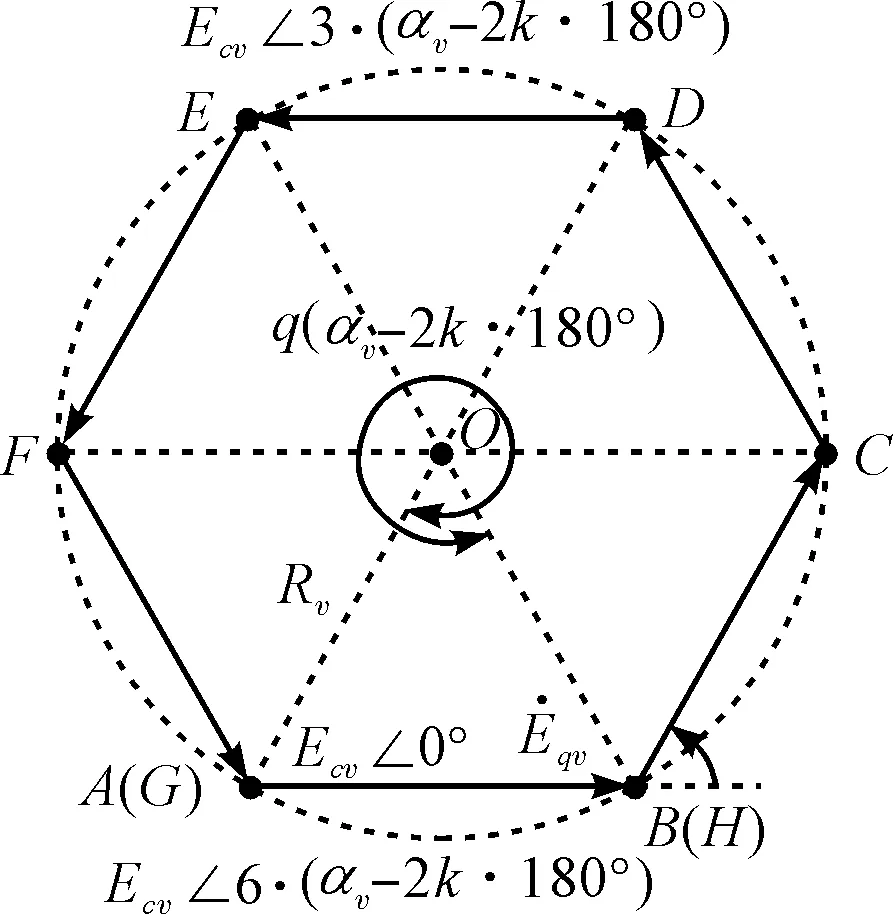
π(k=0,1,2,…),则无论αv-2kπ为劣角[即αv-2kπ∈(0,π)],还是αv-2kπ为优角[即αv-2kπ∈(π,2π)],这q个相量按平移求和法则首尾相连后必有外接圆:当αv-2kπ为劣角时,每个相量对应的圆心角均为αv-2kπ,如图2(a)所示;当αv-2kπ为优角时,每个相量对应的圆心角均为(2k+2)π-αv,如图2(b)所示。
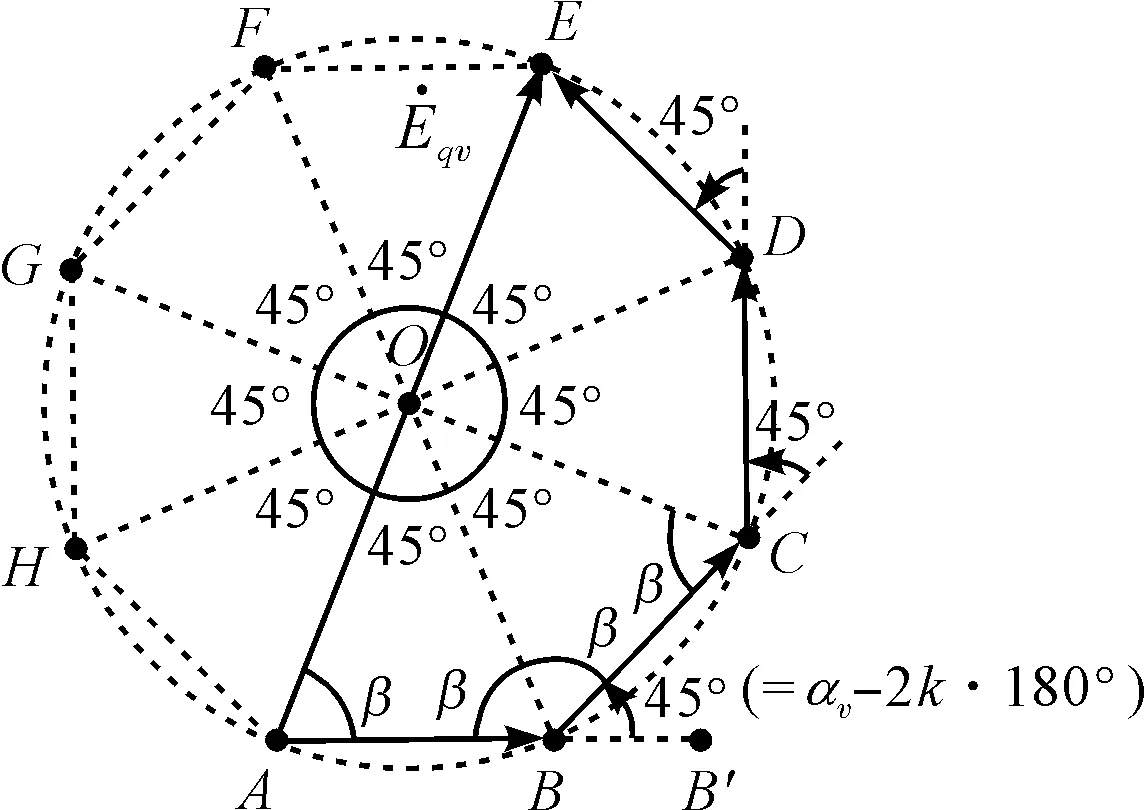
(a)αv-2k·180°为劣角时的情形
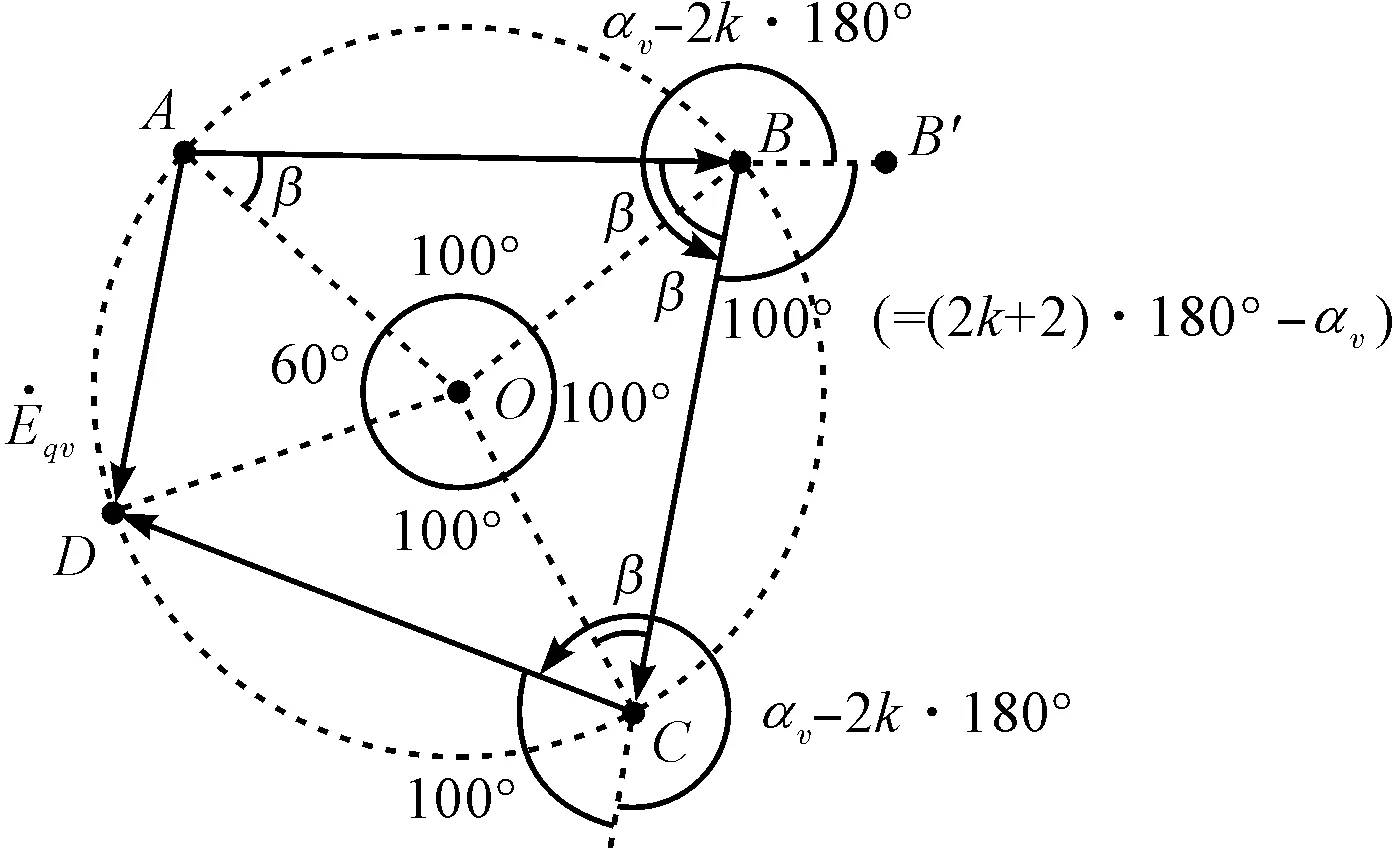
(b)αv-2k·180°为优角时的情形图2 极相组v次谐波电动势相量合成的几何原理
图2(a,b)分别以v=3,q=4,αv-2kπ=π/4和v=13,q=3,αv-2kπ=13π/9为例绘制。
证明:(1)当αv-2kπ为劣角时,即αv-2kπ∈(0,π),则∠ABC=π-(αv-2kπ)∈(0,π),因此点A、B、C不共线,如图2(a)所示;当αv-2kπ为优角时,即αv-2kπ∈(π,2π),则∠ABC=(αv-2kπ)-π∈
(0,π),因此点A、B、C不共线,如图2(b)所示。
过不共线3点A、B、C作⊙O,连接OA、OB、OC、OD:
⟹△OBA≌△OCD⟹OA=OD⟹点D在⊙O上。
同理,点E、F、G…(如果有的话)在⊙O上。
亦即q个等相位差且相位差不为(2k+1)π的非零相量按平移求和法则首尾相连后必有外接圆。
(2)易知每个相量和圆心O所形成的三角形均为等腰三角形,根据三角形全等SSS公理,这些三角形又是全等三角形,如图2所示。所以∠OAB=∠OBA=∠OBC=β

当αv-2kπ为劣角时,∠B′BC=αv-2kπ,亦即每个相量对应的圆心角均为αv-2kπ;当αv-2kπ为优角时,∠B′BC=2π-(αv-2kπ)=(2k+2)π-αv,亦即每个相量对应的圆心角均为(2k+2)π-αv。证毕。
2.3 相量合成研究
下面应用相量合成新理论,并划分区间分别探讨极相组q个线圈v次谐波电动势的相量合成:
(1)相邻两槽间两个线圈v次谐波电动势相量限定为(0,2π)的相位差αv-2kπ是劣角、平角还是优角;
(2)当αv-2kπ为劣角时,极相组q个线圈v次谐波电动势所对圆心角的总和q(αv-2kπ)的角度区间;当αv-2kπ为优角时,同样圆心角的总和q[(2k+2)π-αv]的角度区间;当αv-2kπ为平角时,则不划分子区间。
2.3.1αv-2kπ为劣角的情形
此时0<αv-2kπ<π(k=0,1,2,…),分别讨论如下:
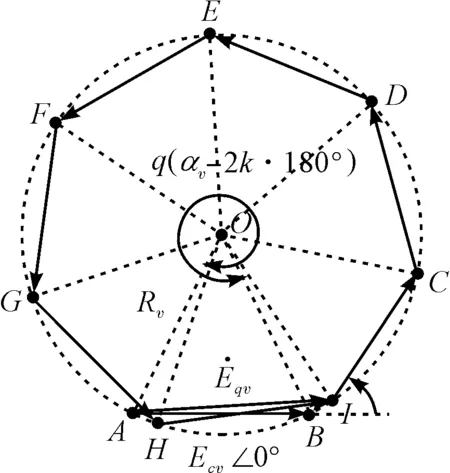
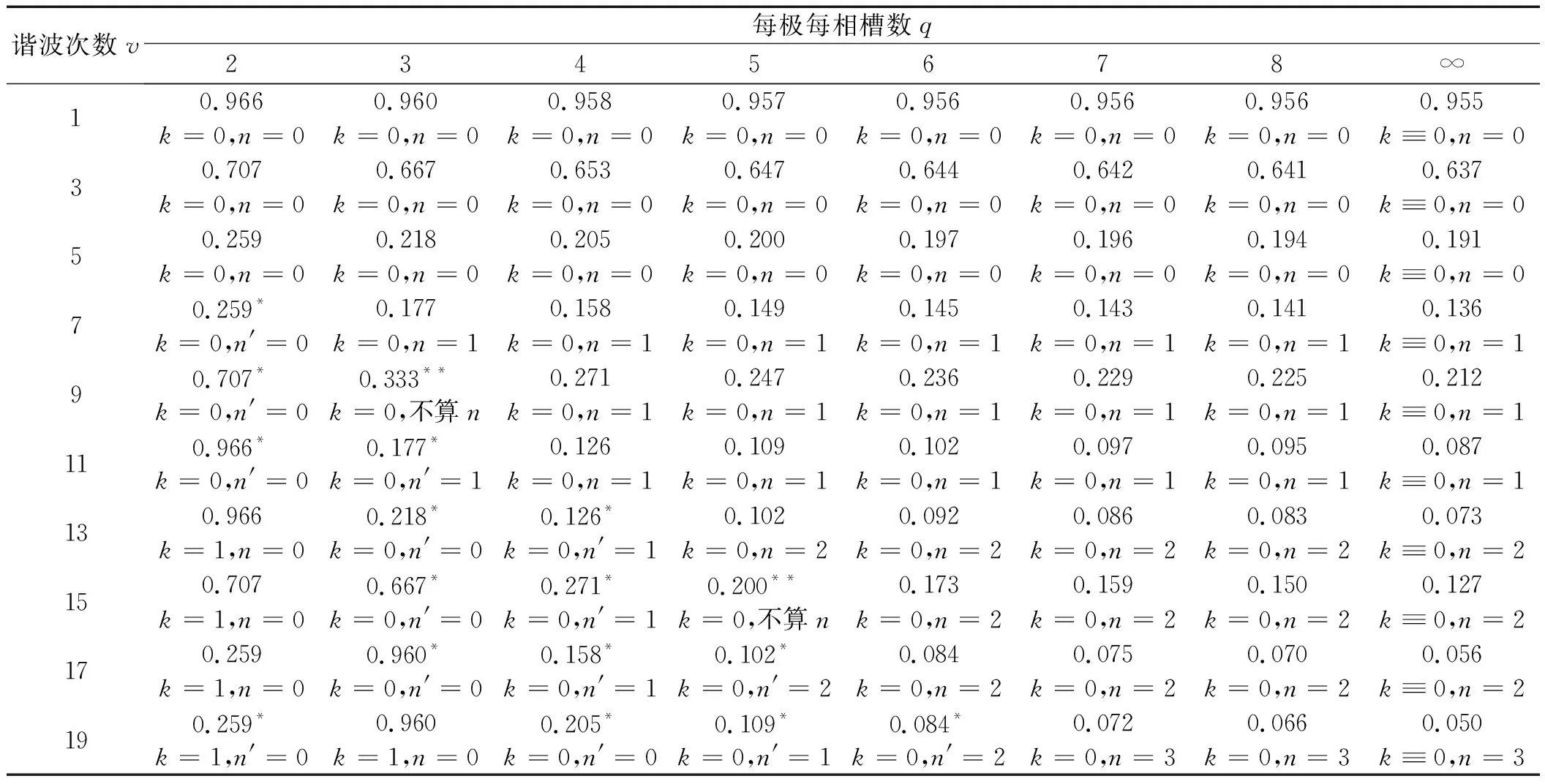
情形一:若0 图3 0°<αv-2k·180°<180°且0° 性质判定:αv-2kπ当q≥2时只能为锐角。 (14) (15) 将Rv代入式(14),可得: (16) 式中:qEcv—q个线圈v次谐波电动势的代数和;kdv—绕组的v次谐波分布因数。 kdv为: (17) 由于Nc匝短距线圈v次谐波电动势的有效值Ecv= 4.44fvNcΦvkpv(参见文献[3]),将其代入式(16),可得极相组v次谐波电动势有效值: Eqv=4.44fv(qNc)Φvkpvkdv=4.44fv(qNc)Φvkwv (18) 式中:qNc—q个线圈的总串联匝数;kwv—整个绕组的v次谐波绕组因数,kwv=kpv×kdv。 情形二:若q(αv-2kπ)=π,即αv=2kπ+(1/q)π,如图4所示(图中v=15,q=2,αv-2kπ=π/2)。 图4 0°<αv-2k·180°<180°且q(αv-2k·180°)=180°时的 性质判定:(1)q≥2;(2)αv-2kπ可为锐角[q≥3,如图2(a)所示]和直角(q=2)。 合成过程分析,合成电动势有效值为: (19) 验证式(17)对情形二的适用性:将αv=2kπ+(1/q)π代入式(17),有: 结论:适用。 情形三:若π 图5 0°<αv-2k·180°<180°且180° 性质判定:(1)q≥2;(2)αv-2kπ可为锐角(q≥4)和钝角(q=2,3)。 合成过程分析,合成电动势有效值为: 即: (20) 情形四:若q(αv-2kπ)=2π(此时必有q>2),即αv=2kπ+(2/q)π,属于2.1节所述劣角中的奇点情形,因此这种情形不存在。下面用反证法证明一般结论,即: q(αv-2kπ)≠2l1π,或αv-2kπ≠(2l1/q)π,l1=1,2,3,…且q>2l1 (21) 证明:假设αv-2kπ=(2l1/q)π,∵0<αv-2kπ<π,即0<(2l1/q)π<π,∴0<2l1 又αv-2kπ=vπ/(mq)-2kπ,∴vπ/(mq)-2kπ=(2l1/q)π,即v=2kmq+2l1m为偶数,这与v为奇数矛盾,故假设不成立,式(21)成立。证毕。 情形五:若2π (a)(q-1)(αv-2k·180°)<360°情形 (b)(q-1)(αv-2k·180°)=360°情形 (c)(q-1)(αv-2k·180°)>360°情形图6 0°<αv-2k·180°<180°且360° 图6(a)中Eqv求解三角形为△AOD,图6(b)中为△AOH,图6(c)中为△AOI。 性质判定:(1)q≥3;(2)q(αv-2kπ)-2π∈(0,π)。 (a)若(q-1)(αv-2kπ)<2π,必有π/(q-1)<αv-2kπ<2π/(q-1)。 (b)若(q-1)(αv-2kπ)=2π,即αv-2kπ=2π/(q-1) 性质判定:m=3时,q≡7,此时v=7(6k+1),αv-2kπ≡π/3(锐角)。 (c)若(q-1)(αv-2kπ)>2π,必有2π/(q-1)<αv-2kπ<3π/(q-1) 图6(a~c)合成过程分析:当2π 即: (22) 情形六:若q(αv-2kπ)=3π,即αv=2kπ+(3/q)π,如图7所示(图中v=9,q=4,αv-2kπ=3π/4)。 图7 0°<αv-2k·180°<180°且q(αv-2k·180°)=540°时的 性质判定:(1)q≥4;(2)αv-2kπ可为锐角(q≥7)、直角(q=6)和钝角(q=4,5)。 合成过程分析,合成电动势有效值: (23) 验证式(22)对情形六的适用性:将αv=2kπ+(3/q)π代入式(22),有: 情形七:若3π 图8 0°<αv-2k·180°<180°且540° 性质判定:(1)q≥4;(2)αv-2kπ可为锐角(q≥8)和钝角(q=4,5,6,7)。 合成过程分析,合成电动势有效值: 即 (24) 情形八:若q(αv-2kπ)=4π(此时必有q>4),即αv=2kπ+(4/q)π,属于2.1节所述劣角中的奇点情形,因此这种情形不存在。 【kdv表达式归纳】:当0<αv-2kπ<π时, 同理可证,若4π …… (25) 式中:k=0,1,2,…且2k+1≤v;n=0,1,2,…且2k+(2n+2)/q≤v。 2.3.2αv-2kπ为优角的情形 此时π<αv-2kπ<2π(k=0,1,2,…),则每个线圈v次谐波电动势相量所对圆心角均为(2k+2)π-αv∈(0,π),采用与2.3.1节相同的方法可证得: 当π<αv-2kπ<2π时,若2n′π (26) 式中:k=0,1,2,…且2k+3≤v;n′=0,1,2,…且2k+2-2n′/q≤v。 2.3.3αv-2kπ为平角的情形 此时αv-2kπ=π或αv=(2k+1)π(k=0,1,2,…),如图9所示。 图9 αv-2k·180°=180°时的 性质判定:∵αv=vπ/(mq)=(2k+1)π,即奇数v能被mq整除,∴q必为奇数。 (27) 现有的谐波电动势分布因数公式为: (28) 为此,经过详细分析并经完全归纳,可得出了新的谐波电动势分布因数公式: (29) 式中:k=0,1,2,…;n=0,1,2,…且2k+(2n+2)/q≤v;n′=0,1,2,…且2k+2-2n′/q≤v。 m=3时,αv=vπ/(mq)=vπ/(3q),αv/2=vπ/(6q);当q→∞时,此时vπ/(6q)→0,有: 由(a)可知:当q→∞时αv无限趋近于0但αv>0,依据新的分布因数公式(29)劣角分支,有:k≡0,n依下式确定:2nπ 运用现有与新的分布因数公式计算三相绕组kdv的结果分别如表(1,2)所示。 表1 现有分布因数公式kdv计算值 表2 新的分布因数公式kdv计算值 1.考虑到一些同步发电机空载电动势波形含有一定分量的17次和19次谐波,表中谐波次数v取到19;2.表2中标*者为公式(29)优角分支计算值,标**者为平角分支计算值,其余为劣角分支计算值 从表1和表2的计算结果对比可知:当v≥7之后,现有公式节距因数均出现了负值,而新的公式则全程未出现负值,后续计算电动势有效值时亦不会为负,符合实际。 针对现有谐波电动势分布因数公式计算电动势有效值出现负值的问题,本文首先建立了分布绕组谐波合成电动势相量模型,根据谐波为奇次的特点提出了极相组相量合成几何原理的新理论,划分区间明确奇点后,应用该理论,并通过相量图分析,研究了v次谐波相邻两槽间夹角αv-2kπ分别为劣角、平角和优角时极相组q个线圈谐波电动势的相量合成(主要关注合成电动势中的分布因数),通过完全归纳,提出了一个对应于αv-2kπ分别为劣角、平角和优角的3分段新分布因数公式,并给出了q→∞的极限形式;其次,选取了三相绕组q=2,…8,∞分别对新旧公式各次谐波进行了数据验证,考虑到一些同步发电机空载电动势波形含有一定分量的17次和19次谐波,验证时截取了1~19次奇次谐波。 验证结果表明:与现有公式当v≥7之后均出现负值不同,新的公式全程未出现负值,说明新公式与实际情况吻合,可替代现有公式使用。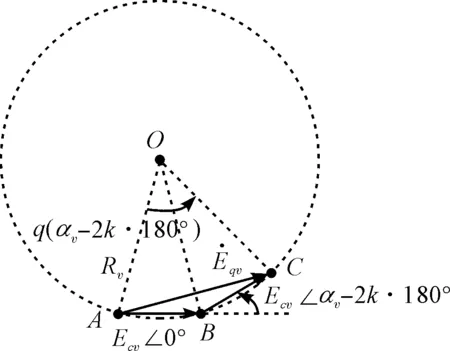
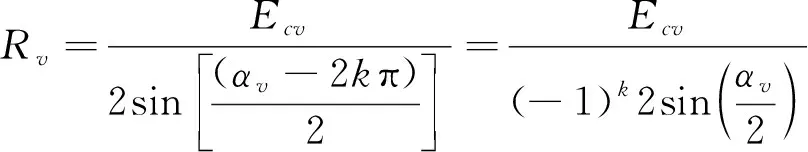



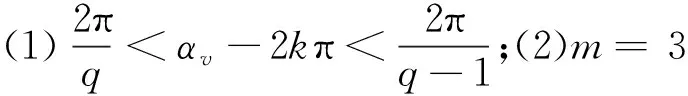
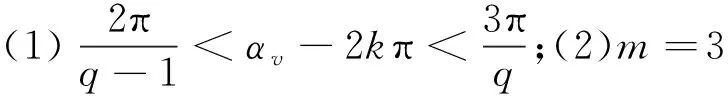
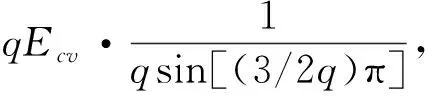
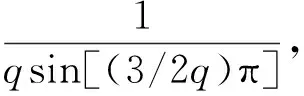


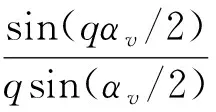
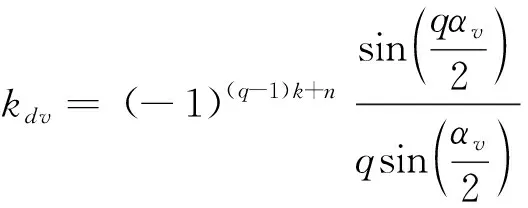
3 新旧分布因数公式的对比与验证
3.1 新旧公式对比
3.2 新旧公式q→∞时的形式比较
3.3 新旧公式验证
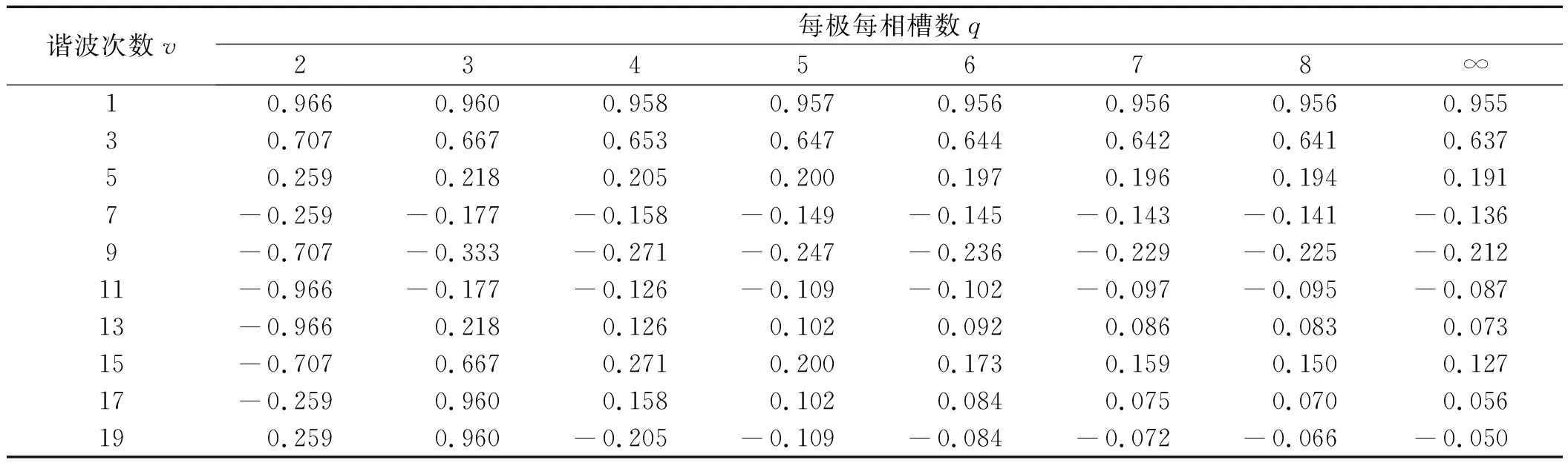
4 结束语

