分布式驱动电动汽车电子差速系统仿真研究*

王亚楠，严世榕，吕兵兵，杨建翠，周海林，刘 战

(福州大学 机械工程及自动化学院，福建 福州 350108)

0 引 言

近年来，分布式驱动电动汽车备受关注，这种驱动方案各轮独立可控，传动效率高，改善了汽车的转向灵活性、操控性和安全性[1]。但汽车在转向时各轮转向半径不同，如不加以控制，会导致汽车转向困难，加剧轮胎磨损，严重时会危及驾驶员和车辆的安全。目前在以转矩为控制目标的电子差速器的设计中，各轮毂电机目标转矩的确定主要采用等值分配的方式，并通过反馈的滑动率进行转矩修正[2-3]，这是一种被动的修正，有一定的时间迟滞，驱动转矩对滑移率的变化过于敏感，且很难产生偏转力矩，导致汽车转向过程中转矩波动大，影响驾驶安全性和乘坐舒适性。

本研究对上述方法进行改进，提出预分配与补偿分配相结合的目标转矩分配方法，并加入路面识别模块，并通过Simulink仿真对该方法进行验证。

1 整车动力学模型

1.1 控制原理

改进后的转矩分配策略的控制原理如图1所示。

图1 电子差速控制原理

路面识别控制器根据各轮实际滑移率和路面利用附着系数识别出当前行驶路面，估算出该路面下的最优滑移率和其对应的峰值附着系数；整车动力学模型根据驾驶员指令和执行机构的反馈计算出当前状态下汽车的横、纵向加速度和所需的总驱动力矩输入转矩预分配模型，转矩预分配模型计算出各轮垂向载荷与整车质量的比值并以此为依据对各轮驱动转矩进行预分配并输送给转矩补偿控制器，转矩补偿控制器根据汽车各轮反馈的实际滑移率与路面识别控制器估算出的该路面下的最优滑移率的差值计算出各轮需要补偿的转矩，与预分配控制器得到的转矩相加后一起输送给轮毂电机；由于电机执行目标转矩信号时会有延迟和误差，这里将轮毂电机输出的实际转矩反馈到电机控制信号的输入端与转矩补偿控制器的输出目标转矩比较，由PID控制器进一步优化控制效果。

1.2 七自由度整车模型

为了不使模型过于复杂又不失准确性，本文建立的整车动力学模型仅考虑对转向影响较大的几个自由度，包括整车纵向运动、横向运动、横摆运动以及4个车轮的旋转运动，共7个自由度[4]。根据牛顿第二定律，可以得到以下动力学方程。

(1)纵向运动动力学方程：

(1)

(2)横向运动动力学方程：

(2)

(3)横摆运动动力学方程：

(3)

(4)各驱动轮的旋转运动动力学方程：

(4)

1.3 轮胎模型

Dugoff轮胎模型所需参数较少，在不同工况下又能较好地模拟真实情况[5]，因此本文选用Dugoff轮胎模型来求解轮胎力。其拟合公式如下：

(5)

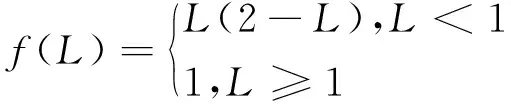
(6)

(7)

式中：λij—各轮纵向滑移率；Kx，Ky—轮胎纵、侧偏刚度；μij—各轮对应的路面附着系数，由路面识别模块提供；ξ—速度影响因子，与轮胎结构和材料有关[6]。

1.4 电机模型

为了简化模型的复杂程度，本文将电机模型简化成传递函数的形式[7]，公式如下：

(8)

2 路面识别控制器

2.1 路面识别原理

汽车在实际行驶时，如不对路面进行识别，电子差速系统很难很好地控制汽车的运行状态，尤其高速运行时极易发生危险。路面识别控制器的输入信号为轮胎实际滑移率和路面利用附着系数，通过与模糊推理模块里存储的标准路面μ-λ曲线对比，输出当前路面下的最优滑移率和其对应的峰值附着系数。

由于本文的研究对象4个轮均为驱动轮，滑移率为：

(9)

式中：vx_ij—各轮中心纵向速度。

各轮中心纵向速度表达式为：

(10)

式中：αij—各轮侧偏角。

路面利用附着系数为：

(11)

式中：Fz_ij—各轮垂向载荷。

2.2 路面识别模块设计

德国的Burckhardt等人[8]通过大量实验数据，拟合出了能够准确描述6种典型路面下轮胎滑移率与路面附着系数的函数关系，μ-λ拟合函数如下：

μ(λ)=C1(1-e-C2λ)-C3λ

(12)

Burckhardt方程中不同路面的拟合系数如表1所示。

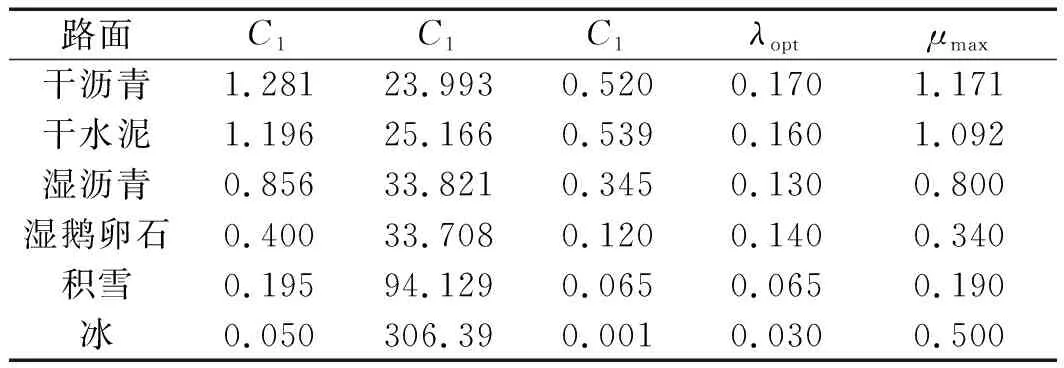
表1 Burckhardt方程中不同路面的拟合系数

表1中的最优滑移率和其对应的路面峰值附着系数为：

(13)

(14)

由式(12)绘制出的Burckhardt标准路面μ-λ曲线如图2所示。

图2 Burckhardt标准路面μ-λ曲线

由图2可以看出：不同路面的最佳滑移率不同，峰值附着系数相去甚远，因此对路面的准确识别是控制器取得良好控制效果的先决条件。

为了提高路面识别的准确性，笔者把6条标准路面曲线作为参考标准，则当前路面的最优滑移率和峰值附着系数[9]为：

(15)

(16)

式中：(λopti,μmaxi)—分别为6条Burckhardt标准曲线对应的最优滑移率和峰值附着系数(见表1)；xi—模糊控制得到的当前路面与6条Burckhardt标准曲线的相似程度，即权重系数。

3 转矩分配控制器的设计

3.1 目标转矩的预分配

轮毂电机目标转矩的预分配基于汽车动力学模型，以方向盘转角和车速为主要输入变量。由于质心到前、后轴的距离不同且受加速度的影响，前、后轴的垂向载荷不同，又由于转向时离心力的作用导致载荷转移，左、右侧车轮的垂直载荷也不同，且车速越高，转向角越大，载荷转移愈明显，地面对轮胎作用力的大小与垂向载荷相关。本研究结合汽车的几何参数和纵、横向加速度，计算出各轮当前状态下的垂向载荷，并以各轮垂向载荷与汽车总质量的比值为依据，对各轮目标驱动力矩进行预分配，最大限度提高车轮驱动力的利用效率。各轮垂向载荷如下：

(17)

式中：ax，ay—汽车的纵、横向加速度。

3.2 目标转矩的补偿分配

汽车在行驶过程中相关参数也处于动态变化中，车轮的滑移率能很好反馈汽车当前的行驶状态，因此引入滑移率的控制对预分配进行补偿修正。此处笔者选取鲁棒性较强的模糊控制对转矩补偿进行分配，该控制器输入端为车轮实际滑移率与当前路面情况下最优滑移率之差，输出端为补偿转矩修正系数，其隶属函数如图(3，4)所示。

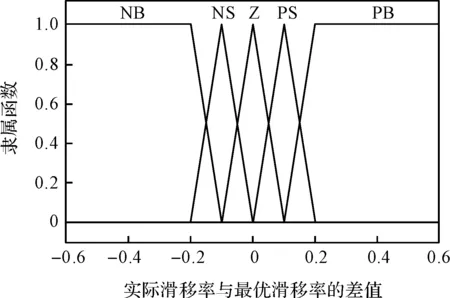
图3 输入端的隶属函数

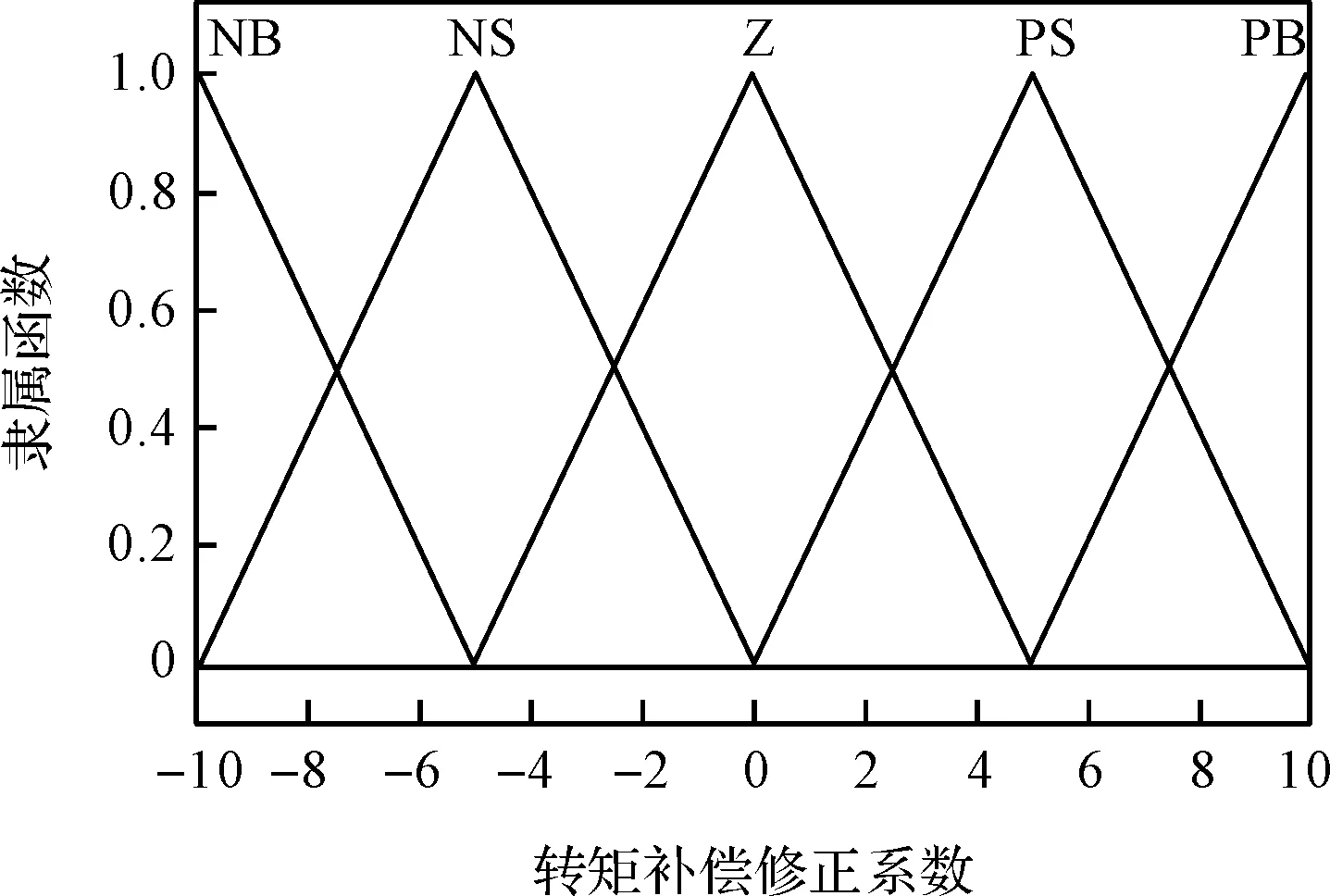
图4 输出端的隶属函数

设定模糊规则如下：

If input is PB，Then output is NB；

If input is PS，Then output is NS；

If input is Z，Then output is Z；

If input is NS，Then output is PS；

If input is NB，Then output is PB；

反复试验调整好量化因子和比例因子，即可完成该控制器的设计。

4 系统仿真分析

4.1 鹅卵石路面对比仿真验证

首先笔者将改进后的控制方法与传统方法进行对比分析。目标路面为湿鹅卵石路面，仿真车速65 km/h，方向盘的转角信号如图5所示。

图5 方向盘转角信号

两种控制策略下各轮滑移率和驱动力矩的变化曲线分别如图(6～9)所示。

图6 传统滑移率分配修正法

图7 改进后的转矩补偿修正法

对比图(6，7)可知，改进后的方法滑移率在最优值附近的波幅更小，汽车行驶更加平稳安全。

图8 传统方法的转矩输出曲线

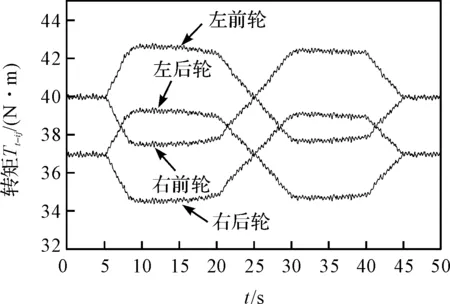
图9 改进方法的转矩输出曲线

由图(8，9)可知：汽车转向行驶时，外侧驱动转矩始终大于内侧，且随着转向角的变化，左、右侧车轮驱动转矩此消彼长，这与转向时的载荷转移相关，与实际情况相符；两图对比可以看出，改进后的转矩补偿分配方法使各轮转矩波动更小，说明转矩对滑移率的敏感程度更低，更有利于汽车的转向稳定性和舒适性。

4.2 高附着路面转向仿真验证

目标路面为干沥青路面，车速设定为100 km/h，方向盘转角为正弦信号，如图10所示。

图10 方向盘转角

汽车的质心侧偏角变化曲线和行驶轨迹分别如图(11，12)所示。

图11 质心侧偏角

由图11知：质心侧偏角随转向角变化而变化，其值一直处于合理范围，且随着控制时间的延长有变小的趋势，有利于汽车的行驶稳定。

由图12知：与传统控制方法相比，改进后的方法使汽车侧向位移更大，说明该控制方法具有更好的转向性能。

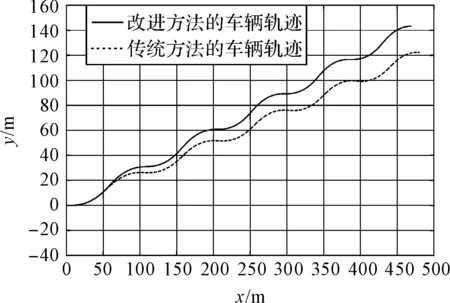
图12 车辆运行轨迹

5 结束语

本文对分布式驱动电动汽车的电子差速控制系统进行了仿真，用Simulink软件建立了七自由度整车动力学、dugoff轮胎、路面识别控制器和转矩分配器等仿真模型，改进了传统仅以滑移率作为转矩分配依据的控制方法，采用更加主动的预分配与补偿分配相结合的控制方法，并进行了模拟仿真。

研究结果表明：该控制系统使各轮滑移率和驱动转矩的波动范围更小，转向效果更理想，同时改善了汽车的转向稳定性、舒适性和安全性。